GSEB Solutions Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.1

Gujarat Board GSEB Solutions Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.1 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.1

Question 1.
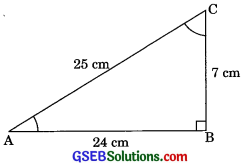
In ΔABC, right angled at B, AB = 24 cm, BC = 7 cm, determine
(i) sin A, cos A
(ii) sin C, cos C
Solution:
We have
AB = 24 cm
BC = 7 cm

(i) In right ΔABC
⇒ AC² = AB² + BC²
⇒ AC² = 24² + 7²
⇒ AC² = 576 + 49

⇒AC² = 625
AC = 25 cm
san A = \(\frac {BC}{AC}\)
sin A = \(\frac {7}{25}\)
cos A = \(\frac {AB}{AC}\) ⇒ cos A = \(\frac {24}{25}\)

(ii) sin C = \(\frac {AB}{AC}\) ⇒ sin C = \(\frac {24}{25}\)
cos C = \(\frac {BC}{AC}\) ⇒ cos C = \(\frac {7}{25}\)

Question 2.
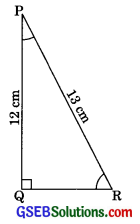
In Fig. find tan P – cot R.

Soution:
In ΔPQR
PR2 = PQ² + QR²
⇒ 13² = 12² + QR²
⇒ 169 = 144 + QR²
⇒ QR² = 169 – 144
⇒ QR² = 25
⇒ QR = 5 cm
tan P = \(\frac {QR}{PR}\) ⇒ tan P = \(\frac {5}{12}\)
⇒ cot R = \(\frac {QR}{PQ}\) ⇒ cot R = \(\frac {5}{12}\)
∴ tan P – cot R = \(\frac {5}{12}\) – \(\frac {5}{12}\) = 0

Question 3.
If sin A = \(\frac {3}{4}\)ca1cu1ate cos A and tan A.
Solution:
We have

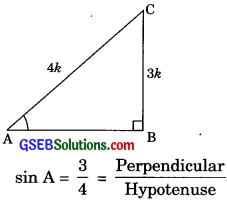
BC = 3k
and AC = 4k
In right ΔABC
AC² = AB² + BC²
(4k)² = AB² + (3k)²
16k² = AB² + 9k²
AB² – 16k² – 9k²
AB² – 7k²
AB = \(\sqrt{7}\) k
∴ cos A = \(\frac{\mathrm{AB}}{\mathrm{AC}}\) = \(\frac{\sqrt{7} k}{4 k}\) = \(\frac{\sqrt{7}}{4}\)
And tan A = \(\frac{\mathrm{BC}}{\mathrm{AB}}\) = \(\frac{3 k}{\sqrt{7} k}\) = \(\frac{3}{\sqrt{7}}\)

Question 4.
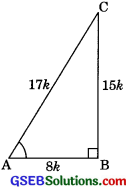
Given 15 cot A = 8 find sin A and sec A.
Solution:
Given 15 cot A = 8,

AB = 8k
and BC = 15k

In right ΔABC,
AC² = AB² + BC²
⇒ AC² = (8k)² +(15k)²
⇒ AC² = 64k² + 225k²
⇒ AC² = 289k²
⇒ AC = 17k
∴ sin A = \(\frac {BC}{AC}\) = \(\frac {15k}{17k}\) = \(\frac {15}{17}\)
and sec A = \(\frac {AC}{AB}\) = \(\frac {17k}{8k}\) = \(\frac {17}{8}\)

Question 5.
Given sec θ = \(\frac {13}{12}\)calculate all other trigono metric ratios.
Solution:
We have

AC = 13k and AB = 12k

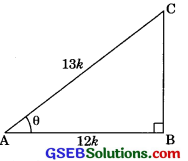
In right ΔABC,
AC² = AB² + BC²
(13k)² = (12k)² + BC²
BC² = 169k² – 144k²
BC² = 25k²
BC = 5k
sin θ = \(\frac {BC}{AC}\) = \(\frac {5k}{13k}\) = \(\frac {5}{13}\)
Cos θ = \(\frac {AB}{AC}\) = \(\frac {12k}{13k}\) = \(\frac {12}{13}\)
tan θ = \(\frac {BC}{AB}\) = \(\frac {5k}{12k}\) = \(\frac {5}{12}\)
cosec θ = \(\frac {AC}{BC}\) = \(\frac {13k}{5k}\) = \(\frac {13}{5}\)
cot θ = \(\frac {AB}{BC}\) = \(\frac {12k}{5k}\) = \(\frac {12}{5}\)

Question 6.
1f ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.
Solution:
Let us consider two right triangles LMN and PQR.
cos A = cos B
\(\frac {PQ}{PR}\) = \(\frac {LM}{LN}\) = k Also = \(\frac {PQ}{LM}\) = \(\frac {PR}{LN}\) …….( 1)
(where k is a positive number)
PQ = kPR
LM = kLN

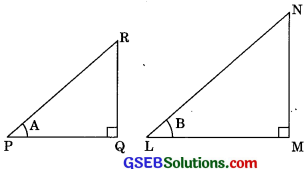
Now, in ΔPQR
PR² = PQ² + QR²
⇒ PR² = (kPR)² + QR²
⇒ QR² = PR² – k²PR²
⇒ QR = \(\sqrt{\mathrm{PR}^{2}-k^{2} \mathrm{PR}^{2}}\)
⇒ QR = PR \(\sqrt{1-k^{2}}\) ……….(2)
In right ΔLMN
LN² = LM² + MN²
⇒ LN² = (kLN)² + MN²
⇒ MN² = LN² – k²LN²
⇒ MN = \(\sqrt{\mathrm{L} \mathrm{N}^{2}-k^{2} \mathrm{L} \mathrm{N}^{2}}\)
⇒ MN = LN\(\sqrt{1-k^{2}}\) ……….(3)
Dividing eqn. (2) by eqn. (3)
\(\frac {QR}{MN}\) = \(\frac{\mathrm{PR} \sqrt{1-k^{2}}}{\mathrm{L} \mathrm{N} \sqrt{1-k^{2}}}\) = \(\frac{Q R}{M N}=\frac{P R}{L N}\) ………..(4)
From equation (1) and (4),
\(\frac{Q R}{M N}=\frac{P R}{L N}=\frac{P Q}{L M}\)
∴ Δ PQR – ΔLMN (by SSS similarity)
∴ ∠PQR = ∠LMN
(corresponding angle of two similar triangles)
∠A = ∠B

Question 7.
If cot θ = \(\frac {7}{8}\) evaluate:
(i) \(\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}\)
(ii) cot² θ
Solution:
We have

AB = 7k and BC = 8k

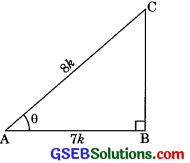
In right ΔABC,
AC² = AB² + BC²
⇒ AC² = (7k)² + (8k)² = 49k² + 64k²
⇒ AC² = 113k²
⇒ AC = \(\sqrt{113 k}\)
sin θ = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{8 k}{\sqrt{113 k}}=\frac{8}{\sqrt{113}}\)
cos θ = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{7 k}{\sqrt{133} k}=\frac{7}{\sqrt{133}}\)

(i) \(\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}\)

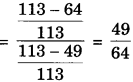
(ii) cot² θ = (cot θ)²
= (\(\frac {7}{8}\))² (cot θ = \(\frac {AB}{BC}\) = \(\frac {7}{8}\))
= \(\frac {49}{64}\)

Question 8.
If 3 cot A =4, check whether
\(\frac{1-\tan ^{2} A}{1+\tan ^{2} A}\) = cos² A – sin² A or not.
Solution:
We have

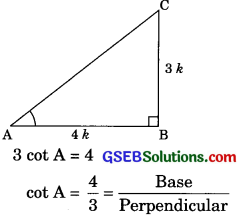
⇒ AB = 4k
⇒ BC = 3k
In right ΔABC,
AC² = AB² + BC²
= (4k)² + (3k)²
= 16k² + 9k²
⇒ AC² = 25k²
⇒ AC = 5k
tan A = \(\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{3 k}{4 k}=\frac{3}{4}\)
sin A = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{3 k}{5 k}=\frac{3}{5}\)
cos A = \(\frac{A B}{A C}=\frac{4 k}{5 k}=\frac{4}{5}\)

RHS = cos²A – sin²A
= (\(\frac {4}{5}\))² – (\(\frac {4}{5}\))²
= \(\frac{16}{25}-\frac{9}{25}=\frac{7}{25}\)
LHS = RHS

Question 9.
In AABC, right angled at B, if tan A = \(\frac{1}{\sqrt{3}}\) ,find the value of
(j) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C
Solution:
We have
tan A = \(\frac{1}{\sqrt{3}}\)
⇒ \(\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{1}{\sqrt{3}}\)
⇒ \(\frac{\mathrm{BC}}{1}=\frac{\mathrm{AB}}{\sqrt{3}}\) = k

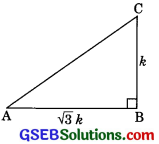
∴ BC = k and AB = \(\sqrt{3} k\)

in right ΔABC
AC² = AB² + BC²
⇒ AC² = (\(\sqrt{3} k\))² + k²
AC² = 3k² + k²
AC² = 4k²
AC = 2k
Now sin A = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{k}{2 k}=\frac{1}{2}\)
Cos A = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\sqrt{3} k}{2 k}=\frac{\sqrt{3}}{2}\)
sin C = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\sqrt{3} k}{2 k}=\frac{\sqrt{3}}{2}\)
Cos C = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{k}{2 k}=\frac{1}{2}\)

(i) sin A cos C + cos A sin C
= \(\frac{1}{2} \times \frac{1}{2}+\frac{\sqrt{3}}{2} \times \frac{\sqrt{3}}{2}\)
= \(\frac{1}{4}+\frac{3}{4}=\frac{1+3}{4}=\frac{4}{4}=1\)

(ii) cos A cos C – sin A sin C
= \(\frac{\sqrt{3}}{2} \times \frac{1}{2}-\frac{1}{2} \times \frac{\sqrt{3}}{2}\)
= \(\frac{\sqrt{3}}{4}-\frac{\sqrt{3}}{4}\) = 0

Question 10.
In APQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the value of sin P, cos P and tan P.
Solution:
In right triangle PQR,
PR² = PQ² + QR² ……..(1)
(By Pythagoras theorem)
PR + QR = 25
⇒ PR = 25 – QR ……….(2)

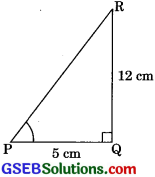
From eqn. (1) and (2)
(25 – QR)² = (5)² + QR²
625 – 2 x 25 x QR + QR²
= 25 + QR²
= 625 – 5O x QR = 5²
– 5O QR = 25 – 625
– 5O QR = – 600
QR = \(\frac{600}{50}\) = 12
Putting in eqn. (2),
PR = 25 – QR = 25 – 12
PR = 13 cm
sin P = \(\frac{QR}{PR}\) = \(\frac{12}{13}\)
cos P = \(\frac{P Q}{P R}=\frac{5}{13}\)
and tan P = \(\frac{Q R}{P Q}=\frac{12}{5}\)

Question 11.
State whether the following are true or false. Justify your answer.
(i) The value of tan A is always less than 1
(ii) sec A = \(\frac{12}{5}\) for some value of A
(iii) cos A is the abbreviation used for the cosecant of angle A
(iv) cot A is the product of cot and A
(v) sin θ = \(\frac{4}{3}\) for some angle.
Solution:
(i) False.

the value of the perpendicular may be longer than the base.

(ii) True

Because Hypotenuse is always greater than the base.

(iii) False
Since cos A is the abbreviation used for the cosine of angle A.

(iv) False
Since cot is meaningless without angle A.

(v) False
Since value of sin O is always less than 1.