This GSEB Class 9 Maths Notes Chapter 6 રેખાઓ અને ખૂણાઓ covers all the important topics and concepts as mentioned in the chapter.
રેખાઓ અને ખૂણાઓ Class 9 GSEB Notes
→ રેખાખંડઃ બે અંત્યબિંદુઓવાળા રેખાના ભાગને રેખાખંડ કહેવાય છે.
→ કિરણઃ એક જ અંત્યબિંદુ ધરાવતા રેખાના ભાગને કિરણ કહેવાય છે.
નોંધઃ રેખાખંડ ABને \(\overline{\mathrm{AB}}\) અને તેની લંબાઈને AB વડે દર્શાવાય છે. કિરણ ABને \(\overrightarrow{\mathrm{AB}}\) દ્વારા અને રેખા ABને \(\overleftrightarrow{\mathrm{AB}}\) દ્વારા દર્શાવાય છે. છતાં પણ આપણે આ સંકેતોનો ઉપયોગ કરીશું નહિ અને રેખાખંડ AB, કિરણ AB, રેખાખંડ ABની લંબાઈ અને રેખા ABને તે જ સંકેત, એટલે કે AB વડે દર્શાવીશું. તમને તેનો અર્થ સંદર્ભથી સ્પષ્ટ થઈ જશે. ક્યારેક ક્યારેક રેખાઓને દર્શાવવા અંગ્રેજીના મૂળાક્ષરો , m, n વગેરેનો ઉપયોગ કરીશું.
→ સમરેખ બિંદુઓ અને અસમરેખ બિંદુઓઃ જો ત્રણ કે ત્રણથી વધારે બિંદુઓ એક જ રેખા પર આવેલા હોય, તો તે બિંદુઓને સમરેખ બિંદુઓ કહેવાય છે. અન્યથા તે અસમરેખ બિંદુઓ કહેવાય છે.
→ ખૂણો, બાજુઓ અને શિરોબિંદુ જ્યારે સામાન્ય અંત્યબિંદુવાળાં બે કિરણોનો ઉદ્ભવ થાય ત્યારે ખૂણો બને છે. અહીં ખૂણો બનાવતાં કિરણોને ખૂણાની બાજુઓ અથવા ભુજ કહેવામાં આવે છે અને સામાન્ય અંત્યબિંદુને ખૂણાનું શિરોબિંદુ કહેવાય છે.
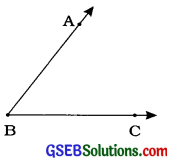
અહીં, સામાન્ય અંત્યબિંદુ Bવાળા બે ભિન્ન કિરણો BA અને BC ખૂણો ABC બનાવે છે. ખૂણા ABCને સંકેતમાં ∠ABC લખાય છે. સંકેત ∠ABC એ ∠ABCનું અંશ માપ પણ દર્શાવે છે. કિરણો BA અને BC એ ∠ABCની બાજુઓ તથા બિંદુ B એ ∠ABCનું શિરોબિંદુ છે.
![]()
→ ખૂણાના પ્રકાર :
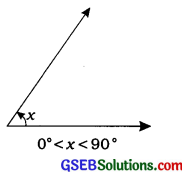
(1) લઘુકોણ (Acute angle): જે ખૂણાનું માપ 0° અને 90°ની વચ્ચે હોય તે ખૂણાને લઘુકોણ કહેવાય છે.
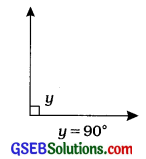
(2) કાટકોણ (Right angle): જે ખૂણાનું માપ 90° હોય તે ખૂણાને કાટકોણ કહેવાય છે.
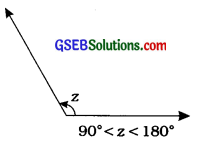
(3) ગુરુકોણ (Obtuse angle): જે ખૂણાનું માપ 90° અને 180°ની વચ્ચે હોય તે ખૂણાને ગુરુકોણ કહેવાય છે.
(4) સરળકોણ (Straight angle): જે ખૂણાનું માપ 180° હોય તે ખૂણાને સરળકોણ કહેવાય છે.
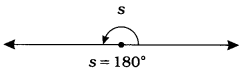
(5) વિપરીતકોણ (Reflex angle): જે ખૂણાનું માપ 180° અને 3600ની વચ્ચે હોય તે ખૂણાને વિપરીતકોણ કહેવાય છે.
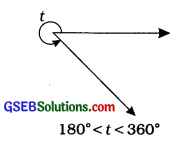
આમ, લઘુકોણનું માપ 0થી 90ની વચ્ચે હોય, કાટકોણનું માપ બરાબર 90° હોય, ગુરુકોણનું માપ 90થી 180° ની વચ્ચે હોય, સરળકોણનું માપ બરાબર 180° હોય અને વિપરીતકોણનું માપ 180થી 360ની વચ્ચે હોય.
→ કોટિકોણ (Complementary angles): જે બે ખૂણાઓના માપનો સરવાળો 90° થાય છે, તે ખૂણાઓને એકબીજાના કોટિકોણ કહે છે.
→ પૂરકકોણ (supplementary angles): જે બે ખૂણાઓના માપનો સરવાળો 180° થાય છે, તે ખૂણાઓને એકબીજાના પૂરકકોણ કહે છે.
જો ∠A = 400, ∠B = 500 અને ∠C = 140° હોય, તો ∠A અને ∠B કોટિકોણ છે તથા ∠A અને ∠C પૂરકકોણ છે.
→ આસનકોણ (Adjacent angles) : જો બે ખૂણાઓનું શિરોબિંદુ એક જ હોય, એક ભુજ સામાન્ય હોય અને સામાન્ય ન હોય તેવા ભુજ એ સામાન્ય ભુજની જુદી જુદી બાજુએ હોય તેવા બે ખૂણાઓને આસન્નકોણ કહેવાય.
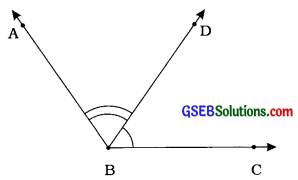
અહીં, ∠ABD અને ∠DBC આસન્નકોણ છે. કિરણ BD તેમનું સામાન્ય ભુજ છે અને B એ બંને ખૂણાનું શિરોબિંદુ છે. કિરણ BA અને કિરણ BC તેમના સામાન્ય ન હોય તેવાં ભુજ છે.
જો બે ખૂણા આસન્નકોણ હોય, તો તેમનાં માપનો સરવાળો તેઓના સામાન્ય ન હોય તેવા ભુજથી બનતા ખૂણાના માપ જેટલો હોય.
અહીં, ∠ABC = ∠ABD + ∠DBC
→ ખૂણાઓની રૈખિક જોડ (Pair of linear angles) : જો બે આસન્નકોણના સામાન્ય ન હોય તેવાં ભુજ એક રેખા બનાવે, તો તેવા ખૂણાઓની જોડને ખૂણાઓની રેખિક જોડ કહેવાય છે.
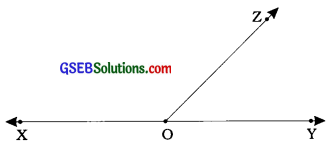
અહીં, આસન્નકોણ ∠XOZ અને ∠ZOYમાં તેમના સામાન્ય ન હોય તેવાં ભુજ OX અને OY રેખા XY બનાવે છે. આથી ∠XOZ અને ∠ZOY એ ખૂણાઓની રેખિક જોડ રચે છે. તેમનો સરવાળો હંમેશાં 180° હોય.
અહીં, ∠XOZ + ∠ZOY = 1800
→ અભિકોણો (Vertically opposite angles) સામાન્ય શિરોબિંદુ ધરાવતા બે ખૂણાઓમાં જો એક ખૂણાનો દરેક ભુજ બીજા ખૂણાના ભુજ સાથે મળીને રેખા બનાવતો હોય, તો તેવા ખૂણાઓને અભિકોણ કહે છે.
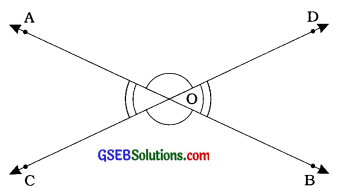
અહીં, રેખાઓ AB અને CD બિંદુ Oમાં છેદે છે. આથી આપણને અભિકોણોની બે જોડ મળે છે. ∠AOC અને ∠BOD દ્વારા અભિકોણોની જોડ બને છે તેમજ ∠AOD અને ∠BOC દ્વારા પણ અભિકોણોની જોડ બને છે. અભિકોણો હંમેશાં સમાન હોય છે.
અહીં, ∠AOC = ∠BOD અને ∠AOD = ∠BOC.
![]()
→ પૂર્વધારણા 6.1: જે કિરણનું ઉદ્ભવબિંદુ રેખા પર હોય તેવાં કિરણ અને રેખાથી બનતાં બંને ખૂણાઓનો સરવાળો 1800 થાય છે.
→ પૂર્વધારણા 6.2: જો બે આસન્નકોણોનો સરવાળો 180° હોય, તો તેની સામાન્ય ન હોય તેવી બાજુઓ એક રેખા બનાવે છે. સ્પષ્ટ કારણોસર, ઉપરની બંને પૂર્વધારણાઓ એકત્રિત કરતાં તેમને સંયુક્ત રૂપે રેખિક જોડની પૂર્વધારણા કહે છે.
→ પ્રમેય 6.1: પરસ્પર છેદતી બે રેખાથી બનતા અભિકોણ સમાન હોય છે.
ઉદાહરણ : 1.
આપેલ આકૃતિમાં રેખાઓ AB અને CD બિંદુ માં છેદે છે. જો ∠APC: ∠BPC = 7:8 હોય, તો તમામ ખૂણા શોધો.
ઉત્તર:
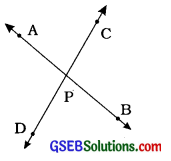
∠APC + ∠BPC = 1800 (રૈખિક જોડ)
પરંતુ ∠APC: ∠BPC = 7: 8
ગુણોતરોનો સરવાળો = 7 + 8 = 15
તેથી ∠APC = \(\frac{7}{15}\) × 1800 = 840
અને ∠BPC = \(\frac{8}{15}\) × 180° = 96°
હવે ∠BPD = ∠APC = 84° ([ì4()
અને ∠APD = ∠BPC = 96° (t[Lt)
ઉદાહરણ : 2.
આપેલ આકૃતિમાં કિરણ Yw રેખા XYZ પર છે. ∠WYZ: ∠WYX = 1: 2 છે. કિરણ YQ તથા કિરણ YP અનુક્રમે ∠WYZ અને ∠WYXના દ્વિભાજક છે. ∠PYQ શોધો.
ઉત્તર:
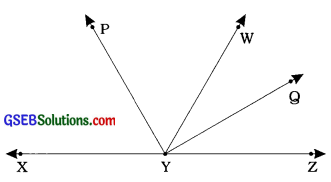
∠WYZ + ∠WYX = 180° (રૈખિક જોડ)
∠WYZ: ∠WYX = 1 : 2
ગુણોત્તરોનો સરવાળો = 1 + 2 = 3
માટે, ∠WYZ = \(\frac{1}{3}\) × 180° = 60°
અને ∠WYX = \(\frac{2}{3}\) × 180° = 120°
હવે, કિરણ YQ એ wYZ નો દ્વિભાજક છે.
∴ ∠WYQ = ∠WYZ = 2 × 60° = 30°
તે જ રીતે, કિરણ YP એ ∠WYXનો દ્વિભાજક છે.
∴ ∠WYP = ∠WYX = \(\frac{1}{2}\) × 120° = 60°
હવે, ∠PYQ = ∠WYO + ∠WYP (આસનકોણ)
∴ ∠PYQ = 30° + 60° = 90°
ઉદાહરણ : 3.
આપેલ આકૃતિમાં AB ⊥ CD છે. જો x : y : z = 4 : 5 : 6 હોય, તો x, y અને z માપ શોધો.
ઉત્તર:
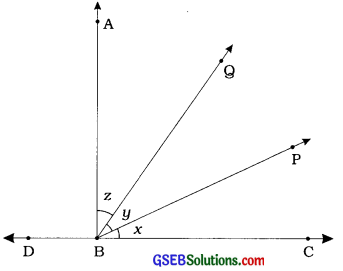
અહીં, AB ⊥ CD છે.
∴ ∠ABC = 90°
x + y + z = 90° (આસન્નકોણ)
વળી, x : y : z = 4 : 5 : 6
ગુણોત્તરોનો સરવાળો = 4 + 5 + 6 = 15
∴ x = \(\frac{4}{15}\) × 90° = 24°
y = \(\frac{5}{15}\) × 90° = 30°
z = \(\frac{6}{15}\) × 90° = 36°
→ સમાંતર રેખાઓ અને છેદિકા:
છેદિક જે રેખા બે અથવા બેથી વધુ રેખાઓને ભિન્ન બિંદુઓમાં છેદે છે, તેને આ રેખાઓની છેદિકા કહે છે.
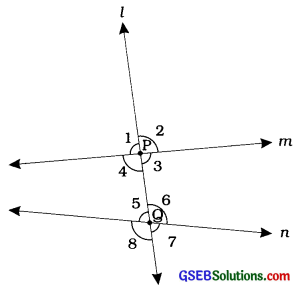
રેખા ! એ રેખાઓ m અને nને અનુક્રમે P અને ઉમાં છેદે છે. તેથી રેખા ! એ રેખા m અને nની છેદિકા છે. તમે જોશો કે પ્રત્યેક બિંદુ P અને હુ આગળ ચાર ખૂણાઓનું નિર્માણ થાય છે.
- આ ખૂણાઓને આપણે આકૃતિમાં દર્શાવ્યા મુજબ ∠1, ∠2, ∠3, ∠4, ∠5, ∠6, ∠7 અને ∠8 કહીશું. ∠1, ∠2, ∠7 અને ∠8ને બહિષ્કોણો Exterior angle) કહે છે.
- જ્યારે ∠3, ∠4, ∠5 અને ∠6ને અંતઃકોણો (Interior angle) કહે છે.
![]()
→ અનુકોણ (Corresponding angles) છેદિકાની એક જ તરફ આવેલ એક બહિષ્કોણ અને એક અંતઃકોણ જો રેખિક જોડ રચતા ન હોય તો તેવા ખૂણાઓને અનુકોણની જોડ કહે છે. પ્રત્યેક ખૂણો બીજા ખૂણાનો અનુકોણ કહેવાય છે.
અહીં આપણને અનુકોણની ચાર જોડ મળે છે ∠1 અને ∠5, ∠2 અને ∠6, ∠4 અને ∠8 તથા ∠3 અને ∠7.
→ અંતયુમકોણ (Interior alternate angles) છેદિકાની વિરુદ્ધ બાજુએ આવેલા બે અંતઃકોણો જો રેખિક જોડ રચતા ન હોય તો તેવા ખૂણાઓને અંતયુગ્મકોણની જોડ કહે છે. પ્રત્યેક ખૂણો બીજા ખૂણાનો અંત યુગ્મકોણ કહેવાય છે.
- અહીં, ∠4 અને ∠6 તથા ∠3 અને ∠5 અંત યુગ્મકોણની જોડ રચે છે.
- ઘણી વખત અંતઃયુગ્મકોણને યુગ્મકોણ કહેવામાં આવે છે.
→ બહિર્મુગ્મકોણ (exterior alternate angles) : છેદિકાની વિરુદ્ધ બાજુએ આવેલા બે બાહ્યકોણો જો રેખિક જોડ રચતા ન હોય તો તેવા ખૂણાઓને બહિર્મુગ્મકોણની જોડ કહે છે. પ્રત્યેક ખૂણો બીજા ખૂણાનો બહિગ્સકોણ કહેવાય છે.
અહીં, ∠1 અને ∠7 તથા ∠2 અને ∠8 બહિર્મુગ્મકોણની જોડ રચે છે.
→ છેદિકાની એક તરફના અંતઃકોણ (Interior angles on the same side of transversal) : છેદિકાની એક જ તરફ આવેલ બે અંતઃકોણોને છેદિકાની એક તરફના અંતઃકોણ કહે છે. “ અહીં, 24 અને 25 તથા ∠3 અને ∠6 છેદિકાની એક તરફના અંતઃકોણ છે.
છેદિકાની એક તરફના અંતઃકોણને અનુક્રમિક અંતઃખૂણા (Consecutive interior angles) અથવા સંબંધિતકોણ અથવા સહઆંતરિક ખૂણા પણ કહે છે.
→ સમાંતર રેખાઓની છેદિકા દ્વારા બનતા ખૂણાઓની જોડના સંબંધોઃ
→ પૂર્વધારણા 6.3 : જો એક છેદિકા બે સમાંતર રેખાઓને છેદે, તો અનુકોણની પ્રત્યેક જોડ સમાન હોય છે. પૂર્વધારણા 6.3ને અનુકોણ પૂર્વધારણા પણ કહેવામાં આવે છે.
→ પૂર્વધારણા 6.4: જો એક છેદિકા બે રેખાઓને એ રીતે છેદે કે અનુકોણની એક જોડ સમાન હોય, તો બંને રેખાઓ પરસ્પર સમાંતર હોય છે.
→ પ્રમેય 6.2 : જો એક છેદિકા બે સમાંતર રેખાઓને છેદે, તો અંત યુગ્મકોણની પ્રત્યેક જોડ સમાન હોય છે.
→ પ્રમેય 6.3 : જો એક છેદિકા બે રેખાઓને એવી રીતે છેદે કે અંતયુગ્મકોણોની એક જોડ સમાન હોય, તો બંને રેખાઓ પરસ્પર સમાંતર હોય છે.
→ પ્રમેય 6.4: એક છેદિકા બે સમાંતર રેખાઓને છેદે તો છેદિકાની એક જ તરફના અંતઃકોણોની પ્રત્યેક જોડ પૂરક હોય છે.
→ પ્રમેય 6.5: જો એક છેદિકા બે રેખાઓને એવી રીતે છેદે કે છેદિકાની એક જ તરફના અંતઃકોણોની એક જોડ પૂરક હોય, તો બંને રેખાઓ પરસ્પર સમાંતર હોય છે. એક જ રેખાને સમાંતર રેખાઓ
→ પ્રમેય 6.6 : જે રેખાઓ એક જ રેખાને સમાંતર હોય તે પરસ્પર સમાંતર હોય છે.
ઉદાહરણ : 1.
આપેલ આકૃતિમાં જો AB ∥ CD, ∠BMX = 125° અને ∠CNX = 55° હોય, તો ∠MXN શોધો.
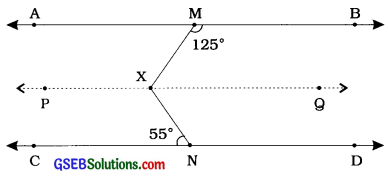
ઉત્તર:
Xમાંથી પસાર થતી ABને સમાંતર હોય તેવી રેખા PQ દોરો.
AB ∥ CD અને AB ∥ PQ
આથી CD ∥ PO
હવે, ∠BMX + ∠MXQ = 180° (AB ∥ POની છેદિકા MX દ્વારા બનતા છેદિકાની એક જ બાજુના અંતઃકોણ)
∴ 125 + Z MXQ =180°
∴ ∠ MX = 550 …. (1)
હવે, ∠NXQ = ∠XNC (CD ∥ PQ, યુગ્મકોણ)
∴ ∠NXQ = 550 … (2)
હવે, ∠MXN = ∠MXQ + ∠NXg (આસન્નકોણ)
∴ ∠MAN = 55° + 55° (પરિણામ (1) અને (2))
∴ ∠MXN = 110°
ઉદાહરણ : 2.
આપેલ આકૃતિમાં જો PQ ∥ RS અને RS ∥ TU તથા y: 2 = 7: 8 હોય, તો xનું માપ શોધો.
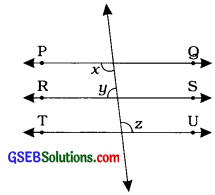
ઉત્તર:
PQ ∥ RS અને RS ∥ TU
∴PQ ∥ TU (પ્રમેય 6.6)
∴ x = z (અંતઃયુગ્મકોણ)
હવે, PQ ∥ RS
∴ x + y = 180° (છેદિકાની એક જ તરફના અંતઃકોણ)
આમ, x = 2 અને x + y = 180°
∴ y + z = 180°
વળી, y : z = 7: 8
ગુણોત્તરોનો સરવાળો = 7 + 8 = 15
∴ y = \(\frac{7}{15}\) × 180° = 84°
અને z = \(\frac{8}{15}\) × 180° = 96°
હવે, x = z = 96°
→ ત્રિકોણના ખૂણાઓના સરવાળાનો ગુણધર્મઃ
પ્રમેય 6.7: ત્રિકોણના ત્રણેય ખૂણાઓનો સરવાળો 180° થાય છે.
![]()
→ ત્રિકોણનો બહિષ્કોણ જો કોઈ ત્રિકોણની કોઈ પણ બાજુને એક તરફ લંબાવવામાં આવે, તો આપણને એક એવો ખૂણો મળે છે કે જે ત્રિકોણના જે શિરોબિંદુ પરથી બાજુ લંબાવવામાં આવી હોય તે શિરોબિંદુ પરના ખૂણા જોડે રેખિક જોડ રચે છે. આવા ખૂણાને ત્રિકોણનો બહિષ્કોણ કહે છે. બીજા શબ્દોમાં, ત્રિકોણના કોઈ પણ ખૂણા સાથે રેખિક જોડ રચતા ખૂણાને ત્રિકોણનો બહિષ્કોણ કહે છે.
→ પ્રમેય 6.8: જો ત્રિકોણની એક બાજુને લંબાવવામાં આવે, તો આ પ્રકારે બનેલ બહિષ્કોણ બંને અંતઃસંમુખ કોણ(Interior opposite angles)ના સરવાળાને સમાન થાય છે.
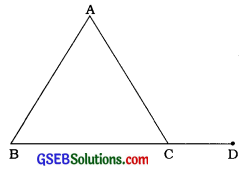
અહીં, ∠ACD એ ΔABCનો બહિષ્કોણ છે અને તેથી ∠ACD = ∠A + ∠B.
ઉદાહરણ : 1.
ΔABCમાં ∠A: ∠B: ∠C = 5: 7: 8 હોય, તો ΔABCના દરેક ખૂણાનું માપ શોધો.
ઉત્તર:
ΔABCમાં ∠A + ∠B + ∠C = 180°
∠A: ∠B: ∠C = 5: 7:8
ગુણોત્તરોનો સરવાળો = 5 + 7 + 8 = 20 .
∴ ∠A = \(\frac{5}{20}\) × 180° = 5 × 9 = 459,
∠B = \(\frac{7}{20}\) × 180° = 7 × 9 = 63°
અને ∠C = \(\frac{8}{20}\) × 180° = 8 × 9 = 72°
ઉદાહરણ : 2.
ΔABCમાં ∠B અને ના દ્વિભાજકો I બિંદુમાં છેદે છે. સાબિત કરો કે, ∠BIC = 90° + \(\frac{1}{2}\)∠A.
ઉત્તર:
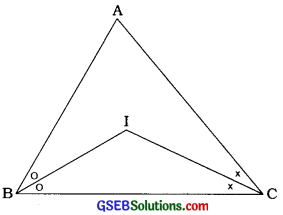
Δ ABCમાં ∠A + ∠ABC + ∠ACB = 180°
∴ ∠ABC + ∠ACB = 180° –ZA ..(1)
ΔABCમાં ∠B અને ∠Cના દ્વિભાજકો 1 બિંદુમાં છેદે છે.
∴ ∠IBC = \(\frac{1}{2}\)∠ABC અને ∠ICB = \(\frac{1}{2}\)∠ACB …. (2)
Δ IBCમાં,
∴ ∠BIC + ∠IBC + ∠ICB = 180°
∴∠BIC = 180°- (∠IBC +∠ICB)
∴ ∠BIC = 1800 – [\(\frac{1}{2}\)∠ ABC + \(\frac{1}{2}\)∠ ACB] ((2) મુજબ)
∴∠BIC = 180°- \(\frac{1}{2}\) (∠ABC + ∠ACB)
∴ ∠BIC = 180°- \(\frac{1}{2}\)(180°- ∠A) ((1) મુજબ)
∴ ∠BIC = 180°- 90° + \(\frac{1}{2}\)∠A
∴ ∠BIC = 90° + \(\frac{1}{2}\)∠A