Gujarat Board GSEB Solutions Class 10 Maths Chapter 3 દ્વિચલ સુરેખ સમીકરણયુગ્મ Ex 3.7 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 10 Maths Chapter 3 દ્વિચલ સુરેખ સમીકરણયુગ્મ Ex 3.7
જ આ સ્વાધ્યાય પરીક્ષા માટે ધ્યાનમાં લેવાનું નથી.
પ્રશ્ન 1.
બે મિત્રો અને અને બીજુની ઉંમરનો તફાવત 3 વર્ષ છે. અનીના પિતા ધરમની ઉંમર (વર્ષમાં) અનીની ઉંમરથી બમણી અને બીજુની ઉંમર (વર્ષમાં) તેની બહેન કેથી કરતાં બે ગણી છે. જો કેથી અને ધરમની ઉંમરના વર્ષનો તફાવત 30 વર્ષનો હોય, તો અની અને બીજુની ઉંમર શોધો.
ઉત્તરઃ
ધારો કે, અનીની ઉંમર x વર્ષ અને બીજુની ઉંમર , વર્ષ છે. તો, આપેલ માહિતી મુજબ
x – y = 3 ………….(1)
અથવા y – x = 3 ………… (2)
ધરમની ઉંમર અનીની ઉંમર કરતાં બમણી છે.
∴ ધરમની ઉંમર = 2x વર્ષ
બીજુની ઉંમર તેની બહેન કેથીની ઉંમરથી બે ગણી છે. એટલે કે કે કેથીની ઉંમર બીજુની ઉંમર કરતાં અડધી છે.
∴ કેથીની ઉંમર = \(\frac{y}{2}\) વર્ષ
સ્વાભાવિક છે કે ધરમની ઉંમર કેથીની ઉંમર કરતાં વધારે છે.
∴ 2x – \(\frac{y}{2}\) = 30
∴ 4x – y = 60 ……….. (3)
(i) પ્રથમ આપણે સમીકરણ (1) અને સમીકરણ (૩)નો ઉકેલ
શોધીએ. સમીકરણ (3)માંથી સમીકરણ (1) બાદ કરતાં,
(4x – y) – (x – y) = 60 – 3
∴ 3x = 57
∴ x = 19
સમીકરણ (1)માં x = 19 મૂકતાં,
19 – y = 3
∴ 19 – 3 = 9
∴ y = 16
આમ, અનીની ઉંમર 19 વર્ષ અને બીજુની ઉંમર 16 વર્ષ થાય.

(ii) હવે આપણે સમીકરણ (2) અને સમીકરણ (3)નો ઉકેલ શોધીએ.
સમીકરણો (2) અને (3)નો સરવાળો લેતાં,
(y – x) + (4x – y) = 3 + 60
∴ 3x = 63
∴ x = 21
સમીકરણ (2)માં x = 21 મૂકતાં,
y – 21 = 3
y = 24
આમ, અનીની ઉંમર 21 વર્ષ અને બીજુની ઉંમર 24 વર્ષ થાય.
આથી અની અને બીજુની ઉંમર અનુક્રમે 19 વર્ષ અને 16 વર્ષ અથવા 21 વર્ષ અને 24 વર્ષ છે.
પ્રશ્ન 2.
એક વ્યક્તિ તેના મિત્રને કહે છે, “જો તું મને સો રૂપિયા આપે, તો મારી પાસે તારાથી બે ગણા રૂપિયા હશે.” બીજો વ્યક્તિ કહે છે, “જો તું મને દસ રૂપિયા આપે, તો મારી પાસે તારાથી છ ગણા રૂપિયા હશે.” અનુક્રમે બંનેની મૂડી રકમ જણાવો. (ભાસ્કર ના બીજગણિતમાંથી)
[સૂચનઃ + 100 = 2 (g-100), પુ + 10 = 6 (x -10)]
ઉત્તરઃ
ધારો કે, પ્રથમ વ્યક્તિ (જેને આપણે A કહીએ) પાસે ₹ x છે અને બીજી વ્યક્તિ (જેને આપણે B કહીએ) પાસે ₹ y છે.
જો B એ A ને ₹ 100 આપે, તો A પાસે ₹ (x + 100) થાય અને B પાસે ₹ (y – 100) થાય.
આપેલ શરત મુજબ,
x + 100 = 2 (y- 100)
∴ x + 100 = 2y – 200
∴ x – 2 = – 300 …………… (1)
જો A એ Bને 10 આપે, તો A પાસે ₹ (x – 10) થાય અને B પાસે ₹ (y + 10) થાય.
આપેલ શરત મુજબ,
y + 10 = 6 (x – 10)
∴ y + 10 = 6x – 60
∴ 10 + 60 = 6x – y
∴ 6x – y = 70 ………..(2)
સમીકરણ (2)ને 2 વડે ગુણતાં,
12x – 2y = 140 ……………(3)
સમીકરણ (3)માંથી સમીકરણ (1) બાદ કરતાં,
(12x – 2y) – (x – 2y) = 140 – (- 300)
∴ 11x = 440
∴ x = 40
સમીકરણ (1)માં x = 40 મૂક્તાં,
40 – 2y = – 300
∴ 40 + 300 = 2y
∴ 2y = 340
∴ y= 170
આમ, પ્રથમ વ્યક્તિ પાસે 40 છે અને બીજા વ્યક્તિ પાસે ₹ 170 છે.

પ્રશ્ન 3.
એક ટ્રેન અચળ ઝડપે ચોક્કસ અંતર કાપે છે. જો ટ્રેનની ઝડપમાં 10 કિમી / કલાક વધારો થાય, તો તે મુસાફરી માટે નક્કી સમય કરતાં 2 કલાક ઓછો સમય લે છે અને ટ્રેનની ઝડપમાં 10 કિમી/કલાકનો ઘટાડો કરતાં, તે મુસાફરી માટે નક્કી સમય કરતાં 3 કલાક વધારે સમય લે છે, તો ટ્રેન દ્વારા કપાયેલું કુલ અંતર શોધો.
ઉત્તરઃ
ધારો કે, ટ્રેનની કાયમી અચળ ઝડપ ૪ કિમી/ કલાક છે અને મુસાફરીનો કાયમી સમય , કલાક છે. આથી ટ્રેન દ્વારા કપાયેલું કુલ અંતર = ઝડપ x સમય = xy કિમી.
હવે, પ્રથમ માહિતી મુજબ, ટ્રેનની નવી ઝડપ = (x + 10) કિમી / કલાક અને નવો સમય = (y – 2) કલાક.
વળી, ઝડપ ૪ સમય = અંતર પરથી
(x + 10) (y – 2) = xy
∴ xy – 2x + 10y – 20 = xy
∴ – 2x + 10y = 20 ………….(1)
તે જ રીતે, દ્વિતીય માહિતી મુજબ, ટ્રેનની નવી ઝડપ = (x – 10) કિમી/ કલાક અને નવો સમય = (y + 3) કલાક.
આથી (x – 10) (y + 3) = xy
∴ xy + 3x – 10y – 30 = xy
∴ 3x – 10y = 30 ………….. (2)
સમીકરણો (1) અને (2)નો સરવાળો લેતાં,
(- 2x + 10y) + (3x – 10y) = 20 + 30
∴ x = 50
સમીકરણ (1)માં x = 50 મૂકતાં,
-2 (50) + 10y = 20
∴ – 100 + 10y = 20
∴ 10y = 120
∴ y = 12
હવે, ટ્રેન દ્વારા કપાયેલું કુલ અંતર = xy = 50 × 12 = 600
કિમી આમ, ટ્રેન દ્વારા કપાયેલું કુલ અંતર 600 કિમી છે.

પ્રશ્ન 4.
એક વર્ગના વિદ્યાર્થીઓને હારમાં ઊભા રાખવામાં આવ્યા છે. દરેક હારમાં 3 વિદ્યાર્થીઓ વધારે ઊભા રાખતાં 1 હાર ઓછી બને છે. 3 વિદ્યાર્થીઓ પ્રત્યેક હારમાં ઓછા ઊભા રાખતાં 2 હાર વધારે બને છે, તો વર્ગખંડમાં રહેલા વિદ્યાર્થીઓની સંખ્યા શોધો.
ઉત્તરઃ
ધારો કે, દરેક હારમાં ઊભા રાખેલ વિદ્યાર્થીઓની સંખ્યા x છે અને કુલ હારની સંખ્યા y છે.
આથી કુલ વિદ્યાર્થીઓની સંખ્યા = xy થાય.
હવે, પ્રથમ માહિતી મુજબ, દરેક હારમાં ઊભા રાખેલ વિદ્યાર્થીઓની સંખ્યા = (x + 3) અને કુલ હારની સંખ્યા = y – 1 થાય.
∴ (x + 3) (y – 1) = xy
∴ xy + 3y – 3 = xy
∴ – x + 3 = 3 ………… (1)
તે જ રીતે, દ્વિતીય માહિતી મુજબ, દરેક હારમાં ઊભા રાખેલ વિદ્યાર્થીઓની સંખ્યા = (x – 3)
અને કુલ હારની સંખ્યા = (y + 2) થાય.
∴ ( x – 3) (y + 2) = xy
∴ xy + 2x – 6 = xy
∴ 2x – 3y = 6 …………… (2)
સમીકરણો (1) અને (2)નો સરવાળો લેતાં,
(- x + 3y) + (2x – 3y) = 3 + 6
∴ x = 9
સમીકરણ (1)માં x = 9 મૂકતાં,
– 9 + 3y = 3
∴ 3y = 12
∴ y = 4
હવે, કુલ વિદ્યાર્થીઓની સંખ્યા = xy = 9 × 4 = 36.
આમ, વર્ગખંડમાં રહેલા વિદ્યાર્થીઓની સંખ્યા 36 છે.

પ્રશ્ન 5.
જો ∆ ABCમાં ∠C = 3∠B = 2 (∠A + ∠B) હોય, તો ત્રિકોણના ત્રણેય ખૂણાઓનાં માપ શોધો.
ઉત્તરઃ
∆ ABC માટે ∠A + ∠B + 20 = 180°
∴ ∠A + ∠B + 3∠B = 180° ( ∠C = 3∠B)
∠A + 4∠B = 180° ………… (1)
વળી, ∠A + ∠B + ∠ C = 180°
∴ ∠A + ∠B + 2 (∠A + ∠B) = 180° (∵ AC = 2 (∠A + ∠B))
∴ 3(∠A + ∠B) = 180°
∴ ∠A + ∠B = 60° ………… (2)
સમીકરણ (1)માંથી સમીકરણ (2) બાદ કરતાં,
(∠A + 4∠B) – (∠A + ∠B) = 180° – 60°
∴ 3∠B = 120° .
∴ ∠B = 40°
સમીકરણ (2)માં ∠B = 40° મૂકતાં,
∠A + 40° = 60° .
∴ ∠A = 20°
∠C = 3∠Bમાં ∠B = 40° મૂકતાં
∠C = 3 (40°)
∴ ∠C = 120°
આમ, ∆ ABCમાં, ∠A = 20°; ∠B = 40° અને ∠C = 120°.
નોંધઃ
સમીકરણ ∠A+ ∠B + ∠Cમાં ∠A + ∠B = \(\frac{\angle \mathrm{C}}{2}\) મૂકીને એક જ ચલ 20નું સરળ સમીકરણ \(\frac{3}{2}\) ∠C = 180° મેળવીને પણ ઉકેલ શોધી શકાય. ∠C શોધ્યા બાદ ∠B અને ∠A પણ સરળતાથી શોધી શકાય.

પ્રશ્ન 6.
સમીકરણો 5x – y = 5 અને 3x – y = 3 દ્વારા દર્શાવાતી રેખાના આલેખ દોરો. પુ-અક્ષ અને બંને રેખાઓ દ્વારા બનતા ત્રિકોણનાં શિરોબિંદુઓ જણાવો.
ઉત્તરઃ
5x – y = 5 પરથી, y = 6x – 5 મળે.

3x – y = 3 પરથી, y = 3x – 3 મળે.

હવે, આપણે બંને સમીકરણના આલેખ એક જ આલેખપત્ર પર છે દોરીએ.
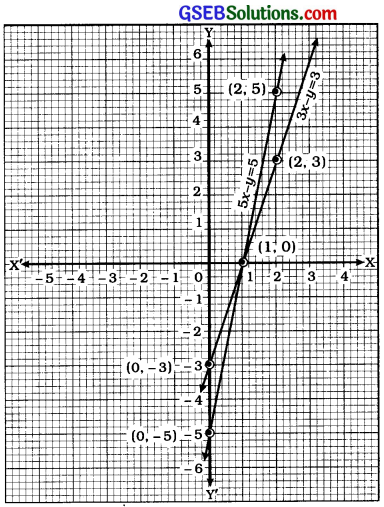
આલેખમાંથી સ્પષ્ટ છે કે પુ-અક્ષ અને બંને સમીકરણોની રેખાઓ દ્વારા બનતા ત્રિકોણના શિરોબિંદુઓ (1, 0) (0, -3) અને (0, -5) છે.

પ્રશ્ન 7.
નીચેનાં સુરેખ સમીકરણયુમ ઉકેલોઃ
(i) px + qy = p – q
qx – py = P + q
(ii) ax + by = c
bx + ay = 1 + c
(iii) \(\frac{x}{a}-\frac{y}{b}\) = 0
ax + by = a2 + b2
(iv) (a – b) x + (a + b) y = a2 – 2ab – b2
(a + b) (x + y) = a2 + b2
(v) 152x – 378y = – 74
– 378x + 152y = – 604.
ઉત્તરઃ
(i) px + qy = p – q ……………..(1)
qx – Py = p + q …………..(2)
સમીકરણ (1)ને રૂ વડે અને સમીકરણ (2)ને q વડે ગુણતાં,
p2x + pqy = p2 – pq …….. (3)
qx – pqy = pq + q2 ………… (4)
સમીકરણો (3) અને (4)નો સરવાળો લેતાં,
(p2x + pqy) + (qx – pqy) = (p2 – pq) + (pq + q2)
∴ x (p2 + q2) = p2 + q2
∴ x = 1
સમીકરણ (1)માં x = 1 મૂક્તાં,
p(1) + qy = p – q
∴ qy = – q
∴ y = -1
આમ, આપેલ સમીકરણયુગ્મનો ઉકેલ x = 1, y = – 1 છે.

(ii) ax + by = c ……… (1)
bx + ay = 1 + c ………. (2)
સમીકરણ (1)ને વડે અને સમીકરણ (2)ને b વડે ગુણતાં,
a2x + aby = ac …… (3)
b2x + aby = b + bc ……… (4)
સમીકરણ (3)માંથી સમીકરણ (4) બાદ કરતાં,
(a2x + aby) – (b2x + aby) = ac – (b + bc)
x (a2 – b2) = ac – b – bc
x = \(\frac{c(a-b)-b}{a^{2}-b^{2}}\)
સમીકરણ (1)માં x = \(\frac{c(a-b)-b}{a^{2}-b^{2}}\) મૂકતાં,
a[latex]\frac{c a-c b-b}{a^{2}-b^{2}}[/latex] + by = c

(iii) \(\frac{x}{a}-\frac{y}{b}\) = 0 …………(1)
ax + by = a2 + b2 ………… (2)
સમીકરણ (1) મુજબ,
\(\frac{x}{a}=\frac{y}{b}\)
y = \(\frac{b}{a}\) x
સમીકરણ (2) માં y = \(\frac{b}{a}\) x મૂકતાં,
ax + (\(\frac{b}{a}\)x) = a2 + b2
ax + \(\frac{b^{2}}{a}\) x = a2 + b2
∴ x(a + \(\frac{b^{2}}{a}\)) = a2 + b2
∴ x = a
y = \(\frac{b}{a}\) x માં x = a મૂકતાં,
y = \(\frac{b}{a}\) (a)
∴ y = b
આમ, આપેલ સમીકરણયુગ્મનો ઉકેલ x = a, y = b છે.

(iv) (a – b) x + (a + b) y = a2 – 2ab – b2 ………. (1)
(a + b) (x + y) = a2 + b2
∴ (a + b) x + (a + b) y = a2 + b2 ……………. (2)
સમીકરણ (2)માંથી સમીકરણ (1) બાદ કરતાં,
[(a + b) x + (a + b) y] – [(a -b) x + (a + b) y] = (a2 + b2) – (a2 – 2ab – b2)
x (a + b – a + b) = a2 + b2 – a2 + 2ab + b x (2b) = 2ab + 2b
∴ x(2b) = 2ab + b2
સમીકરણ )માં x = a + b મૂકતાં,
(a – b) (a + b) + (a + b) y = a2 – 2ab – b2
∴ a – b + (a + b) y = a2 – 2ab – b2
∴ (a + b) y = – 2ab
∴ y = – \(\frac{2 a b}{a+b}\)
આમ, આપેલ સમીકરણયુગ્મનો ઉકેલ x = a + b, y = – \(\frac{2 a b}{a+b}\) છે.
(v) 152x – 378y = – 74 …………(1)
– 378x + 152y = – 604 …………..(2)
સમીકરણો (1) અને (2)નો સરવાળો લેતાં,
– 226x – 226y = – 678
∴ x + y = 3 (-226 વડે ભાગતાં) ………………..(3)
સમીકરણ (1)માંથી સમીકરણ (2) બાદ કરતાં,
(152x – 378) – (- 378x + 152y) = (- 74) – (- 604)
∴ 530x – 530y = 530
∴ x – y = 1 (530 વડે ભાગતાં) …… (4)
સમીકરણો (3) અને (4)નો સરવાળો લેતાં,
2x = 4
∴ x = 2
સમીકરણ (3)માં x = 2 મૂક્તાં, 2 + y = 3
∴ y = 1
આમ, આપેલ સમીકરણયુગ્મનો ઉકેલ x = 2, y = 1 છે.

પ્રશ્ન 8.
જો ABCD ચક્રીય ચતુષ્કોણ હોય (આકૃતિ જુઓ), તો તે ચક્રીય ચતુષ્કોણના ખૂણાઓ 03-5 શોધો.
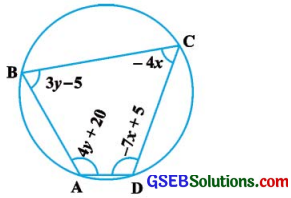
ઉત્તરઃ
ABCD ચક્રીય ચતુષ્કોણ છે.
∴ ∠A + ∠C = 180° અને
2B + ∠D = 180°.
∠A + ∠C = 180° પરથી, 4y + 20° – 4x = 180° મળે.
∴ 40 – 4x = 160°
∴ y – x = 40° (4 વડે ભાગતાં) …………… (1)
∠B + ∠D = 180° પરથી
3y – 5° – 7x + 5 = 180° મળે.
∴ 3y – 7x = 180° …………. (2)
સમીકરણ (1)માંથી y = x + 40° મળે.
સમીકરણ (2)માં y = x + 40° મૂકતાં,
3(x + 40°) – 7x = 180°
∴ – 3x + 120° – 7x = 180°
∴ – 4x = 60°
∴ x = – 15°
સમીકરણ (1)માં x = 15° મૂકતાં,
y – (- 15) = 40°
∴ y + 15° = 40°
∴ y = 25°
હવે, ∠A = 4y + 20° = 4 (25) + 20° = 120°,
∠B = 30 – 5° = 3 (25) – 5° = 70°,
∠C = – 4x = – 4 (- 15°) = 60° અને
∠D = – 7x + 5 = – 7 (- 15°) + 5 = 110°
આમ, આપેલ ચક્રીય ચતુષ્કોણ ABCDમાં,
∠A = 120°, ∠B = 70°, ∠C = 60°, ∠D = 110°.