Gujarat Board GSEB Solutions Class 8 Maths Chapter 13 સમપ્રમાણ અને વ્યસ્ત પ્રમાણ Ex 13.2 Textbook Exercise Questions and Answers.
Gujarat Board Textbook Solutions Class 8 Maths Chapter 13 સમપ્રમાણ અને વ્યસ્ત પ્રમાણ Ex 13.2
1. નીચેનામાંથી કયાં વિધાનો વ્યસ્ત પ્રમાણમાં છે?
પ્રશ્ન (i)
કોઈ એક કામમાં કારીગરોની સંખ્યા અને કામ પૂરું કરવા માટે લાગતો સમય.
જવાબ:
જો કારીગરોની સંખ્યામાં વધારો થાય, તો કામ પૂરું કરવા લાગતો સમય ઘટે.
∴ આ વિધાન વ્યસ્ત પ્રમાણ દર્શાવે છે.
![]()
પ્રશ્ન (ii)
યાત્રા કરવા માટેનો કુલ સમય અને અચળ ઝડપથી કાપેલું અંતર.
જવાબ:
અહીં ઝડપ અચળ છે. તેથી લાગતો સમય ઝડપના સમપ્રમાણમાં હોય.
∴ આ વિધાન વ્યસ્ત પ્રમાણ દર્શાવતું નથી.
પ્રશ્ન (iii)
એક ખેતરનું ક્ષેત્રફળ અને તેમાંથી લીધેલ પાકનો જથ્થો.
જવાબ:
ખેતરનું ક્ષેત્રફળ વધુ હોય, તો તેમાંથી લીધેલો પાક વધુ હોય તથા ક્ષેત્રફળ ઓછું હોય, તો લીધેલો પાક ઓછો હોય. આ સમપ્રમાણ દર્શાવે છે.
∴ આ વિધાન વ્યસ્ત પ્રમાણ દર્શાવતું નથી.
પ્રશ્ન (iv)
એક નિશ્ચિત યાત્રા માટે લાગતો સમય અને વાહનની ઝડપ.
જવાબ:
અહીં વાહનની ઝડપ વધારવામાં આવે તો લાગતો સમય ઘટે.
∴ આ વિધાન વ્યસ્ત પ્રમાણ દર્શાવે છે.
![]()
પ્રશ્ન (v)
કોઈ એક દેશની કુલ જનસંખ્યા અને વ્યક્તિ દીઠ જમીનનું ક્ષેત્રફળ.
જવાબ:
જો જનસંખ્યા વધે તો વ્યક્તિ દીઠ જમીનનું ક્ષેત્રફળ ઘટે તથા જનસંખ્યા ઘટે તો વ્યક્તિ દીઠ જમીનનું ક્ષેત્રફળ વધે.
∴ આ વિધાન વ્યસ્ત પ્રમાણ દર્શાવે છે.
પ્રશ્ન 2.
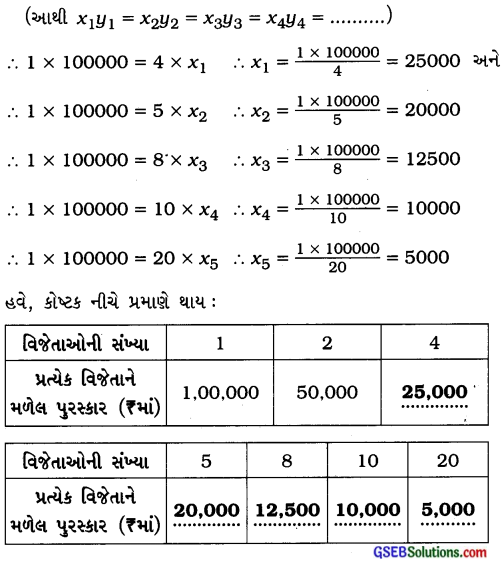
એક ટેલિવિઝન ગેમ શો (game show)માં પુરસ્કારની રકમ 1,00,000 દરેક વિજેતાને સરખા ભાગે વહેંચવામાં આવે છે. નીચે દર્શાવેલા કોષ્ટકને પૂર્ણ કરો અને જણાવો કે કોઈ એક વ્યક્તિગત વિજેતાને મળેલી પુરસ્કારની રકમ કુલ વિજેતાઓની સંખ્યાના સમપ્રમાણમાં છે કે વ્યસ્ત પ્રમાણમાં છે?
જવાબ:
અહીં જણાય છે કે જેમ વિજેતાઓની સંખ્યા વધે છે તેમ દરેકને મળતા પુરસ્કારની રકમ ઘટે છે.
∴ અહીં આ વિગત વ્યસ્ત પ્રમાણમાં છે.
![]()
પ્રશ્ન 3.
રહેમાન, એક પૈડામાં આરા (Spokes) લગાવે છે. આ માટે તે સમાન લંબાઈના આરાનો ઉપયોગ કરે છે. હવે તે આરા એવી રીતે લગાવે છે કે જેથી બે ક્રમિક આરા વચ્ચે બનતો ખૂણો સમાન હોય. હવે તેને નીચે આપેલ કોષ્ટક પૂર્ણ કરીને મદદ કરો:
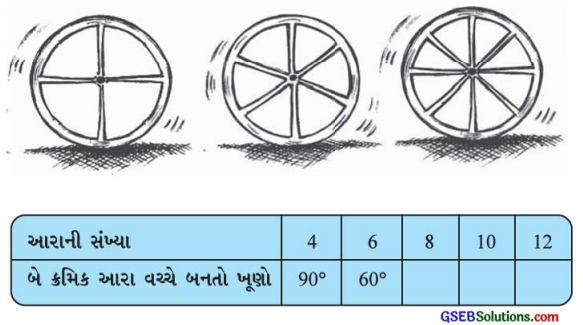
પ્રશ્ન (i)
શું આરાની સંખ્યા અને બે ક્રમિક આરા વચ્ચે બનતો ખૂણો પરસ્પર વ્યસ્ત પ્રમાણમાં છે?
જવાબ:
અહીં કોષ્ટક પરથી જણાય છે કે બે ક્રમિક આરા વચ્ચે બનતો ખૂણો જેમ નાનો કરવામાં આવે છે તેમ આરાની સંખ્યા વધતી જાય છે.
આમ, અહીં વ્યસ્ત પ્રમાણ છે.
∴ કદાચ વ્યસ્ત પ્રમાણ હોઈ શકે. તેની ચકાસણી કરીએ.
અહીં x1 = 4, y1 = 90 અને x2 = 6, y2 = 60
x1y1 = 4 × 90 = 360 અને x2y2 = 6 × 60 = 360
હા, આમ, x1y1 = x2y2 થતા હોવાથી અહીં વ્યસ્ત પ્રમાણ ચોક્કસ છે.
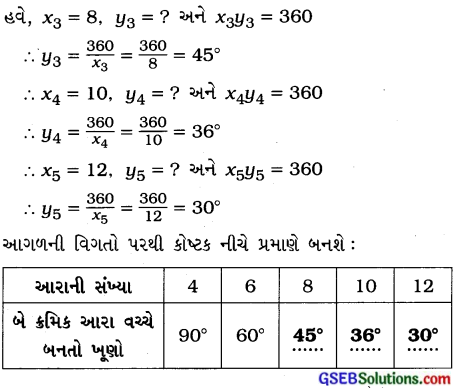
પ્રશ્ન (ii)
15 આરાવાળા એક પૈડામાં બે ક્રમિક આરાની જોડ વચ્ચે બનતા ખૂણાનું માપ શોધો.
જવાબ:
15 આરાવાળા એક પૈડામાં બે ક્રમિક આરાની જોડ વચ્ચે બનતા ખૂણાનું માપ શોધીએ.
ધારો કે, તે ખૂણાનું માપ x° છે.
∴ 15 × x° = 4 × 90°
∴ x° = \(\frac{4 \times 90^{\circ}}{15}\) = 24°
આમ, તે ખૂણાનું માપ 24° હોય.
![]()
પ્રશ્ન (iii)
બે ક્રમિક આરાની જોડ વચ્ચે બનતા ખૂણાનું માપ 40° છે, તો આરાની સંખ્યા શોધો.
જવાબ:
બે ક્રમિક આરાની જોડ વચ્ચે બનતા ખૂણાનું માપ 40° છે, તો આરાની સંખ્યા શોધીએ.
ધારો કે, તે આરાની સંખ્યા x છે.
∴ n × 40° = 4 × 90°
∴ n = \(\frac{4 \times 90^{\circ}}{40^{\circ}}\) = 9.
આમ, તે આરાની સંખ્યા 9 હોય.
પ્રશ્ન 4.
ડબામાં રહેલી મીઠાઈને 24 બાળકો વચ્ચે વહેંચતાં પ્રત્યેક બાળકને મીઠાઈના 5 ટુકડા મળે છે. હવે જો બાળકોની સંખ્યામાં 4નો ઘટાડો થાય, તો પ્રત્યેક બાળકને કેટલી મીઠાઈ મળશે?
જવાબ:
ડબામાં રહેલી મીઠાઈને 24 બાળકો વચ્ચે વહેચાય છે, તો દરેક બાળકને મીઠાઈના 5 ટુકડા મળે છે.
અહીં બાળકોની સંખ્યા x1 = 24 અને દરેકને મળતા મીઠાઈના ટુકડા y1 = 5
હવે, બાળકોની સંખ્યામાં 4નો ઘટાડો થાય છે.
આથી હવે બાળકોની સંખ્યા x2 = 24 – 4 = 20
હવે, દરેક બાળકને મળતા મીઠાઈના ટુકડા y2 = ?
બાળકોની સંખ્યા ઘટે તેમ દરેક બાળકને મળતી મીઠાઈના ટુકડાની સંખ્યા વધે.
∴ અહીં વ્યસ્ત પ્રમાણ છે.
x1 × y1 = x2 × y2
∴ 24 × 5 = 20 × y2
∴ y2= \(\frac{24 \times 5}{20}\) = 6
આમ, દરેક બાળકને મીઠાઈના 6 ટુકડા મળે.
પ્રશ્ન 5.
એક ખેડૂત પાસે 20 પશુઓને 6 દિવસ સુધી ખવડાવી શકાય તેટલો ઘાસચારો છે. હવે જો તેની પાસે 10 પશુઓ વધારે આવે, તો આ ઘાસચારો કેટલા દિવસ ચાલશે?
જવાબ:
ખેડૂત પાસે હાલમાં પશુઓની સંખ્યા x1 = 20 અને ઘાસચારો ચાલે તે દિવસો y1 = 6.
હવે, ખેડૂત પાસે 10 પશુઓ વધારે આવે છે.
∴ ખેડૂત પાસે પશુઓની સંખ્યા x2 = 20 + 10 = 30
હવે, ઘાસચારો ચાલે તે દિવસો y2 = ?
પશુઓની સંખ્યા જેમ વધે તેમ ઘાસચારો ચાલવાના દિવસો ઘટે.
∴ અહીં વ્યસ્ત પ્રમાણ છે.
∴ x1 × y1 = x2 × y2
∴ 20 × 6 = 30 × y2
∴ y2 = \(\frac{20 \times 6}{30}\) = 4
આમ, પશુઓને ઘાસચારો 4 દિવસ ચાલશે.
![]()
પ્રશ્ન 6.
એક ઠેકેદાર અંદાજ મૂકે છે કે જશમિંદરના ઘરે ફરીથી વીજતાર લગાવવાનું કામ 3 વ્યક્તિ, 4 દિવસમાં પૂરું કરી શકે છે. હવે જો તે 3ના બદલે 4 વ્યક્તિને આ કામ પર લગાવે તો આ કામ કેટલા દિવસમાં પૂરું થાય?
જવાબ:
વીજતાર લગાવવા આવનાર વ્યકિતઓ x1 = 3 અને કામ પૂરું કરતાં લાગતાં દિવસ y1 = 4
હવે, કામ કરવા 4 વ્યક્તિઓ લગાવાય છે.
એટલે કે 1 વ્યક્તિ કામ પર વધુ આવે છે.
કામ કરનાર વ્યક્તિઓ x2 = 4 અને કામ પૂરું કરવા લાગતા દિવસ y2 = ?
કામ કરનાર વ્યક્તિઓ વધતાં કામ પૂરું થવાના દિવસો ઘટે.
અહીં વ્યસ્ત પ્રમાણ છે.
x1 × y1 = x2 × y2
3 × 4 = 4 × y2
y2 = \(\frac{3 \times 4}{4}\) = 3
આમ, કામ ૩ દિવસમાં પૂરું થાય.
પ્રશ્ન 7.
એક જથ્થામાં રહેલી શીશીઓને, 1 બૉક્સમાં 12 શીશીઓ હોય તેવાં 25 બૉક્સમાં રાખવામાં આવેલ છે. હવે જો આ જથ્થાની શીશીઓને એવી રીતે રાખવામાં આવે કે જેથી પ્રત્યેક બૉક્સમાં 20 શીશીઓ હોય, તો આવાં કેટલાં બૉક્સ ભરાશે?
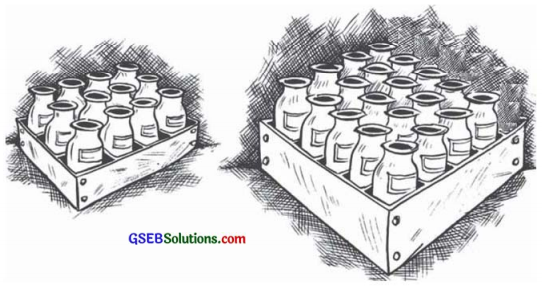
ઉત્તરઃ
1 બૉક્સમાં ભરાતી શીશીઓ x1 = 12 અને આવાં ભરવામાં આવતાં બૉક્સ y1 = 25
હવે, બૉક્સમાં ભરવામાં આવતી શીશીઓ x2 = 20, તો ભરી શકાતાં બૉક્સ y2 = ?
બૉક્સમાં જેમ શીશીઓ વધુ ભરીએ તેમ જરૂરી બૉક્સની સંખ્યા ઘટે.
∴ અહીં વ્યસ્ત પ્રમાણ છે.
∴ x1 × y1 = x2 × y2
∴ 12 × 25 = 20 × y2
∴ y2 = \(\frac{12 \times 25}{20}\) = 15
આમ, આવાં 15 બૉક્સ ભરાશે.
પ્રશ્ન 8.
એક ફેક્ટરીમાં નિશ્ચિત સંખ્યાની વસ્તુઓ 63 દિવસમાં બનાવવા 42 યંત્રોની જરૂર પડે છે. આ જ સંખ્યાની વસ્તુઓ 54 દિવસમાં બનાવવા કેટલાં યંત્રો જોઈએ?
ઉત્તરઃ
નિશ્ચિત સંખ્યાની વસ્તુઓ બનાવવા જરૂરી યંત્રો x1 = 42 અને આ કામ પૂરું કરતાં લાગતા દિવસ છે y1 = 63
હવે, આ જ સંખ્યાની વસ્તુઓ 54 દિવસમાં બનાવવાની છે. y2 = 54
તે માટે કેટલાં યંત્રો જોઈએ તે શોધવું છે. ∴ x2 = ?
હવે, દિવસોની સંખ્યા ઘટે તેમ યંત્રો વધુ જોઈએ.
∴ અહીં વ્યસ્ત પ્રમાણ છે.
∴ x1 × y1 = x2 × y2
∴ 42 × 63 = x2 × 54
∴ x2 = \(\frac{42 \times 63}{54}\) = 49
આમ, 49 યંત્રો જોઈશે.
![]()
પ્રશ્ન 9.
એક કારને 60 કિમી / કલાકની ઝડપથી કોઈ એક સ્થાન પર પહોંચવા માટે 2 કલાકનો સમય લાગે છે. હવે જો કારની ઝડપ 80 કિમી / કલાક હોય, તો કેટલો સમય લાગશે?
ઉત્તરઃ
કારની અગાઉની ઝડપ x1 = 60 કિમી / કલાક છે અને ચોક્કસ સ્થળે પહોંચવા લાગતો સમય છે y1 = 2 કલાક છે.
હવે, કારની ઝડપ x2 = 80 કિમી | કલાક કરવામાં આવે છે, તો નિશ્ચિત સ્થળે પહોંચવામાં લાગતો સમય y2 = ? કારની ઝડપ વધારવામાં આવે તેમ નિશ્ચિત સ્થળે પહોંચવામાં સમય ઓછો લાગે.
∴ અહીં વ્યસ્ત પ્રમાણ છે.
∴ x1 × y1 = x2 × y2
∴ 60 × 2 = 80 × y2
∴ y2 = \(\frac{60 \times 2}{80}=\frac{3}{2}\)
\(\frac{3}{2}=1 \frac{1}{2}\) કલાક
આમ, કારને 1 \(\frac{1}{2}\)કલાક લાગશે.
પ્રશ્ન 10.
એક ઘરમાં નવી બારીઓ લગાવવા માટે 2 વ્યક્તિઓને 3 દિવસ લાગે છે.
પ્રશ્ન (i)
કાર્યની શરૂઆતમાં જ એક વ્યક્તિ બીમાર પડે, તો કાર્ય પૂરું કરવામાં કેટલો સમય લાગશે?
જવાબ:
નવી બારીઓ લગાવવા આવવાના માણસોની સંખ્યા x1 = 2, તેમને
કામ પૂરું કરવા લાગવાના દિવસો y1 = 3
હવે, 1 વ્યક્તિ બીમાર પડે છે.
∴ કામ કરવા આવનાર વ્યક્તિઓની સંખ્યા x2= 2 – 1 = 1, તેમને કામ પૂરું કરવા લાગવાના દિવસો y2 = ?
અહીં કામ કરવા આવનાર વ્યક્તિઓ ઘટે તેમ કામ પૂરું કરવા લાગતા દિવસો વધે.
∴ અહીં વ્યસ્ત પ્રમાણ છે.
∴ x1 × y1 = x2 × y2
∴ 2 × 3 = 1 × y2
∴ y2 = \(\frac{2 \times 3}{1}\) = 6
આમ, કામ પૂરું કરવામાં 6 દિવસ લાગશે.
પ્રશ્ન (ii)
એક જ દિવસમાં બારીઓ લગાવવા કેટલી વ્યક્તિઓની જરૂર પડશે?
જવાબ:
ઉપરની વિગત પરથી x1 × y1 = 2 × 3
હવે, કામ 1 દિવસમાં પૂરું કરવું છે.
∴ y2 = 1, x2 = ?
∴ x1 × y1 = x2 × y2
∴ 2 × 3 = x2 × 1
∴ x2 = \(\frac{2 \times 3}{1}\) = 6
આમ, 1 દિવસમાં કામ પૂરું કરવા 6 વ્યક્તિઓની જરૂર પડશે.
![]()
પ્રશ્ન 11.
કોઈ એક શાળામાં 45 મિનિટનો એક એવા 8 તાસ છે. હવે જો શાળામાં 9 તાસ કરવા હોય, તો દરેક તાસનો સમય કેટલો રાખવો પડે? (અહીં, શાળાનો સમય સમાન રહે છે તેવું માનવું.)
જવાબ:
શાળાનો સમય નિશ્ચિત (સમાન) છે.
શાળામાં દિવસના તાસ x1 = 8 છે અને દરેક તાસનો સમય y1 = 45 મિનિટ છે.
હવે, શાળામાં દિવસના તાસ x2 = 9 કરાય, તો દરેક તાસનો સમય y2 = ?
અહીં તાસની સંખ્યા વધે, તો દરેક તાસ માટેનો સમય ઘટે.
∴ અહીં વ્યસ્ત પ્રમાણ છે.
∴ x1 × y1 = x2 × y2
∴ 8 × 45 = 9 × y2
∴ y2 = \(\frac{8 \times 45}{9}\) = 40
આમ, દરેક તાસનો સમય 40 મિનિટ રાખવો પડે.
