This GSEB Class 9 Maths Notes Chapter 8 ચતુષ્કોણ covers all the important topics and concepts as mentioned in the chapter.
ચતુષ્કોણ Class 9 GSEB Notes
→ ચતુષ્કોણ gિuadrilateral) : ચાર સમતલીય (એક જ સમતલમાં આવેલાં) બિંદુઓ પૈકી કોઈ પણ ત્રણ બિંદુઓ સમરેખ ન હોય, તો તેવાં ચાર બિંદુઓને ક્રમમાં જોડવાથી મળતી બંધ આકૃતિને ચતુષ્કોણ કહે છે.
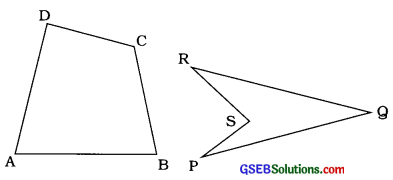
ચાર બિંદુઓને ક્રમમાં જોડવાથી આકૃતિમાં બતાવેલ છે તેવાં બે પ્રકારના ચતુષ્કોણ મળી શકે. ચતુષ્કોણ ABCDને બહિર્મુખ ચતુષ્કોણ (Convex quadrilateral) કહે છે અને ચતુષ્કોણ PQRSને અંતર્મુખ ચતુષ્કોણ (Concave quadrilateral) કહે છે.
આપણે ફક્ત બહિર્મુખ ચતુષ્કોણનો જ અભ્યાસ કરવાનો છે. ચતુષ્કોણને ચાર બાજુઓ, ચાર ખૂણા અને ચાર શિરોબિંદુઓ હોય છે.
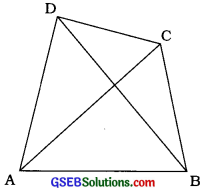
ચતુષ્કોણ ABCDમાં AB, BC, CD અને DA બાજુઓ છે, ∠A, ∠B, ∠C અને ∠D ખૂણાઓ છે તથા A, B, C અને D શિરોબિંદુઓ છે.
ચતુષ્કોણના સામસામેનાં બે શિરોબિંદુઓ જોડવાથી ચતુષ્કોણના વિકર્ણ મળે. ચતુષ્કોણ ABCDમાં AC અને BD વિકર્ણ છે.
ચાર બાજુઓ, ચાર ખૂણા અને બે વિકર્ણને ચતુષ્કોણનાં અંગો કહે છે.
→ ચતુષ્કોણના ખૂણાઓના સરવાળાનો ગુણધર્મ: ચતુષ્કોણના ખૂણાઓનો સરવાળો 360° છે.
એટલે કે, ચતુષ્કોણ XYZWમાં, ∠X + ∠Y + ∠Z + ∠W = 360°.
![]()
→ ચતુષ્કોણના પ્રકાર :
- સમલંબ ચતુષ્કોણ (Trapezium) : જે ચતુષ્કોણમાં સામસામેની બાજુઓની એક જ જોડ સમાંતર હોય તેને સમલંબ ચતુષ્કોણ કહે છે.
- સમાંતરબાજુ ચતુષ્કોણ (Parallelogram) જે ચતુષ્કોણમાં સામસામેની બાજુઓની બંને જોડ સમાંતર હોય તેને સમાંતરબાજુ ચતુષ્કોણ કહે છે.
- લંબચોરસ (Rectangle): જે સમાંતરબાજુ ચતુષ્કોણનો એક ખૂણો (તે પરથી બધા જ ખૂણા) કાટખૂણો હોય તેને લંબચોરસ કહે છે.
- સમબાજુ ચતુષ્કોણ (Rhombus) : જે સમાંતરબાજુ ચતુષ્કોણની બધી જ બાજુઓ સમાન હોય તેને સમબાજુ ચતુષ્કોણ કહે છે.
- ચોરસ (Square) જે સમાંતરબાજુ ચતુષ્કોણનો એક ખૂણો (તે પરથી બધા જ ખૂણા) કાટખૂણો હોય અને બધી જ બાજુઓ સમાન હોય તેને ચોરસ કહે છે.
- પતંગાકાર ચતુષ્કોણ (Kite): જે ચતુષ્કોણમાં પાસપાસેની બાજુઓની બે જોડ સમાન હોય અને સામસામેની બાજુઓની જોડ અસમાન હોય તેને પતંગાકાર ચતુષ્કોણ કહે છે.
→ સમાંતરબાજુ ચતુષ્કોણના ગુણધર્મો :
- પ્રમેય 8.1 સમાંતરબાજુ ચતુષ્કોણનો કોઈ પણ વિકર્ણ તેનું બે એકરૂપ ત્રિકોણમાં વિભાજન કરે છે.
- પ્રમેય 8.2 સમાંતરબાજુ ચતુષ્કોણમાં સામસામેની બાજુઓ સમાન હોય છે.
- પ્રમેય 8.3 : જો કોઈ ચતુષ્કોણની સામસામેની બાજુઓની પ્રત્યેક જોડની બાજુઓ સમાન હોય, તો તે ચતુષ્કોણ સમાંતરબાજુ ચતુષ્કોણ છે.
- પ્રમેય 8.4 સમાંતરબાજુ ચતુષ્કોણમાં સામસામેના ખૂણા. સમાન છે.
- પ્રમેય 8.5 : જો ચતુષ્કોણના સામસામેના ખૂણાઓની પ્રત્યેક જોડના ખૂણા સમાન હોય, તો તે ચતુષ્કોણ સમાંતરબાજુ ચતુષ્કોણ છે.
- પ્રમેય 8.6 : સમાંતરબાજુ ચતુષ્કોણના વિકર્ણો પરસ્પર દુભાગે છે.
- પ્રમેય 8.7: જો કોઈ ચતુષ્કોણના વિકણ એકબીજાને દુભાગે, તો તે ચતુષ્કોણ સમાંતરબાજુ ચતુષ્કોણ છે.
- પ્રમેય 8.8: જો ચતુષ્કોણની સામસામેની બાજુઓની એક જોડની બાજુઓ સમાન અને સમાંતર હોય, તો તે ચતુષ્કોણ સમાંતરબાજુ ચતુષ્કોણ છે.
→ જો ચતુષ્કોણમાં
- સામસામેની બાજુઓ સમાન હોય અથવા
- સામસામેના ખૂણાઓ સમાન હોય અથવા
- વિકણ એકબીજાને દુભાગે અથવા
- સામસામેની બાજુઓની કોઈ પણ એક જોડ સમાન અને સમાંતર હોય, તો તે ચતુષ્કોણ
→ સમાંતરબાજુ ચતુષ્કોણ છે. ક લંબચોરસઃ લંબચોરસના વિકણ પરસ્પર ભાગે છે અને સમાન છે. ઉપરોક્ત વિધાનનું પ્રતીપ પણ સાચું છે.
→ સમબાજુ ચતુષ્કોણ સમબાજુ ચતુષ્કોણના વિકણ પરસ્પર કાટખૂણે દુભાગે છે. ઉપરોક્ત વિધાનનું પ્રતીપ પણ સાચું છે.
→ ચોરસ ચોરસના વિકણ પરસ્પર કાટખૂણે દુભાગે છે અને સમાન છે. ઉપરોક્ત વિધાનનું પ્રતીપ પણ સાચું છે.
![]()
→ પતંગાકાર પતંગાકારનો એક વિકર્ણ બીજા વિકર્ણના લંબદ્વિભાજકનો ભાગ છે. ઉપરોક્ત વિધાનનું પ્રતીપ પણ સાચું છે.
ઉદાહરણ : 1.
સાબિત કરો કે, સમાંતરબાજુ ચતુષ્કોણના દરેક વિકર્ણ દ્વારા સમાંતરબાજુ ચતુષ્કોણનું બે એકરૂપ ત્રિકોણોમાં વિભાજન થાય છે.
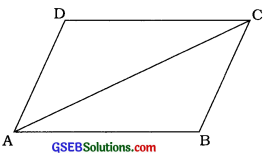
ઉત્તર:
સમાંતરબાજુ ચતુષ્કોણ ABCDના વિકર્ણ AC દ્વારા બે ત્રિકોણ
ΔABC અને ΔCDA મળે છે.
ΔABC અને ΔCDAમાં,
∠CAB = ∠ACD
(AB ∥ CDની છેદિકા AC દ્વારા બનતા યુગ્મકોણ)
∠ACB = ∠CAD
(BC ∥ DAની છેદિકા AC દ્વારા બનતા યુગ્મકોણ)
AC = CA (સામાન્ય)
∴ ખૂબાબૂ શરત મુજબ, ΔABC ≅ ΔCDA
તે જ રીતે વિકર્ણ BD લેતાં,
ΔBCD ≅ ΔDAB મળે.
ઉદાહરણ : 2.
સાબિત કરો કે, સમાંતરબાજુ ચતુષ્કોણના પાસપાસેના બે ખૂણાઓના દ્વિભાજક પરસ્પર લંબ હોય છે.
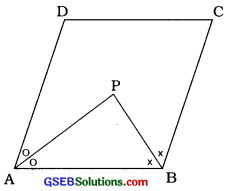
ઉત્તર:
સમાંતરબાજુ ચતુષ્કોણ ABCDના પાસપાસેના ખૂણા ∠A અને ∠Bના દ્વિભાજકો Pમાં છેદે છે.
AP એ ∠DABનો દ્વિભાજક છે.
∠PAB = \(\frac{1}{2}\)∠DAB …………….(1)
BP એ 2 CBAનો દ્વિભાજક છે.
∴ ∠PBA = \(\frac{1}{2}\)∠CBA ………….(2)
(1) અને (2)નો સરવાળો લેતાં,
∠PAB + ∠PBA = \(\frac{1}{2}\)(∠DAB + ∠CBA) ……… (3)
પરંતુ, સમાંતરબાજુ ચતુષ્કોણમાં પાસપાસેના ખૂણા સમાંતર રેખાઓની છેદિકાની એક જ તરફના અંતઃકોણ હોવાથી પૂરકકોણ હોય.
∴ ∠DAB + ∠CBA = 180° ……….(4)
(3) અને (4) પરથી,
∠PAB + ∠PBA = \(\frac{1}{2}\)(180°) = 90°
ΔPABમાં, ∠PAB + ∠PBA + ∠APB = 180°
∴ 90° + ∠APB = 180°
∴ ∠APB = 90°
આથી AP ⊥ BP
ઉદાહરણ : 3.
ચતુષ્કોણ ABCDમાં ∠A : ∠B : ∠C : ∠D = 4 : 5 : 4 : 5 છે, તો ABCDના દરેક ખૂણાનું માપ શોધો તથા ચતુષ્કોણનો પ્રકાર જણાવો.
ઉત્તર:
ચતુષ્કોણ ABCDમાં ∠A + ∠B + ∠C + ∠D = 360°
હવે, ∠A: ∠B: ∠C: ∠D = 4: 5: 4: 5.
ગુણોત્તરોનો સરવાળો = 4 + 5 + 4 + 5 = 18
∠A = \(\frac{4}{18}\) × 360° = 4 × 20° = 80″,
∠B = \(\frac{5}{18}\) × 360° = 5 × 20 = 1000,
∠C = \(\frac{4}{18}\) × 20 = 80°
અને ∠D = \(\frac{5}{18}\) × 360° = 5 × 20° = 100°
ચતુષ્કોણ ABCDમાં ∠A = ∠C અને ∠B = ∠D મળે છે. આથી ABCDના સામસામેના ખૂણાની બંને જોડ સમાન છે. આથી ABCD સમાંતરબાજુ ચતુષ્કોણ છે.
→ ચતુષ્કોણના વિકર્ણોના ગુણધર્મ સ્વાધ્યાય 8.1માં સાબિત કરેલ પરિણામો પરથી નીચેના ગુણધર્મો તારવી શકાય:
- સમાંતરબાજુ ચતુષ્કોણના વિકણ પરસ્પર દુભાગે છે. (પ્રમેય 8.6)
- સમબાજુ ચતુષ્કોણના વિકણે પરસ્પર કાટખૂણે દુભાગે છે.
- લંબચોરસના વિકર્ણો સમાન હોય છે અને પરસ્પર દુભાગે છે.
- ચોરસના વિકર્ણો સમાન હોય છે અને પરસ્પર કાટખૂણે દુભાગે છે. ઉપરોક્ત વિધાનોના પ્રતીપ પણ સાચાં છે.
→ મધ્યબિંદુ પ્રમેયઃ
- પ્રમેય 8.9 ત્રિકોણની બે બાજુઓનાં મધ્યબિંદુઓને જોડતો રેખાખંડ, ત્રીજી બાજુને સમાંતર છે અને તેનાથી અડધો છે.
- પ્રમેય 8.10 ત્રિકોણની એક બાજુના મધ્યબિંદુમાંથી બીજી બાજુને સમાંતર દોરેલી રેખા ત્રીજી બાજુને દુભાગે છે.
→ ચતુષ્કોણની બાજુઓનાં મધ્યબિંદુઓને ક્રમમાં જોડવાથી બનતો ચતુષ્કોણ સમાંતરબાજુ ચતુષ્કોણ છે.
→ સમાંતરબાજુ ચતુષ્કોણની બાજુઓનાં મધ્યબિંદુઓને ક્રમમાં જોડવાથી બનતો ચતુષ્કોણ સમાંતરબાજુ ચતુષ્કોણ છે.
→ સમબાજુ ચતુષ્કોણની બાજુઓનાં મધ્યબિંદુઓને ક્રમમાં જોડવાથી બનતો ચતુષ્કોણ લંબચોરસ છે.
→ લંબચોરસની બાજુઓનાં મધ્યબિંદુઓને ક્રમમાં જોડવાથી બનતો ચતુષ્કોણ સમબાજુ ચતુષ્કોણ છે.
→ ચોરસની બાજુઓનાં મધ્યબિંદુઓને ક્રમમાં જોડવાથી બનતો ચતુષ્કોણ ચોરસ છે.
![]()
ઉદાહરણ : 1.
ΔABCમાં, AB પર M અને AC પર N જ બિંદુઓ એવાં છે કે જેથી AM = \(\frac{1}{4}\)AB અને AM = \(\frac{1}{4}\)AC થાય. સાબિત કરો કે, MN = \(\frac{1}{4}\)BC.
ઉત્તર:
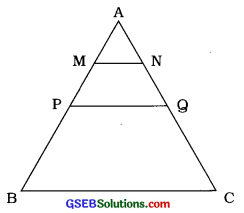
ABનું મધ્યબિંદુ P તથા ACનું મધ્યબિંદુ લઈ તેમને જોડતો રેખાખંડ PQ દોરો.
ΔABCમાં P એ ABનું અને એ ACનું મધ્યબિંદુ છે.
∴ PQ ∥ BC અને PQ = \(\frac{1}{2}\)BC …… (1)
હવે, AP = \(\frac{1}{2}\)AB અને AM = \(\frac{1}{4}\)AB
∴ AM = \(\frac{1}{2}\)AP
તે જ રીતે, AQ = \(\frac{1}{2}\)AC અને AN = \(\frac{1}{4}\)AC.
∴ AN = \(\frac{1}{2}\)AQ
આમ, ΔAPOમાં M એ APનું અને N એ AQનું મધ્યબિંદુ છે.
∴ MN ∥ PQ અને MN = \(\frac{1}{2}\)PQ
હવે, MN = \(\frac{1}{2}\)PQ = \(\frac{1}{2}\)(\(\frac{1}{2}\)BC) ((1) મુજબ)
∴ MN = BC
ઉદાહરણ : 2.
ΔABCમાં, P, Q અને R એ અનુક્રમે AB, BC અને CAનાં મધ્યબિંદુઓ છે. જો AB = 8 સેમી, BC = 6.8 સેમી અને CA = 5.4 સેમી હોય, તો ΔPQRની પરિમિતિ શોધો.
ઉત્તર:
ΔABCમાં, P, Q અને R એ અનુક્રમે AB, BC અને CAનાં મધ્યબિંદુઓ છે.
PQ = \(\frac{1}{2}\)AC = \(\frac{1}{2}\) × 5.4સેમી = 2.7 સેમી,
QR = \(\frac{1}{2}\)AB = \(\frac{1}{2}\) × 8 સેમી = 4 સેમી અને
RP = \(\frac{1}{2}\)BC = \(\frac{1}{2}\) × 6.6 સેમી = ૩.૩ સેમી
Δ PQRની પરિમિતિ = PQ + QR + RP
= 2.7 + 4 + 3.3 સેમી
= 10 સેમી