GSEB Class 9 Maths Notes Chapter 10 વર્તુળ

This GSEB Class 9 Maths Notes Chapter 10 વર્તુળ covers all the important topics and concepts as mentioned in the chapter.

વર્તુળ Class 9 GSEB Notes

→ વર્તુળ અને તેને સંબંધિત પદોઃ વર્તુળ (Circle) સમતલના એક નિશ્ચિત બિંદુથી નિશ્ચિત અંતરે આવેલાં તે સમતલનાં બિંદુઓના સમૂહને વર્તુળ કહે છે. નિશ્ચિત બિંદુને વર્તુળનું કેન્દ્ર (Centre) અને નિશ્ચિત અંતરને વર્તુળની ત્રિજ્યા (Radius) કહે છે.

આપેલ આકૃતિમાં P એ વર્તુળનું કેન્દ્ર છે અને PAની લંબાઈને વર્તુળની ત્રિજ્યા કહે છે. કેન્દ્ર અને વર્તુળના કોઈ પણ બિંદુને જોડતા રેખાખંડને વર્તુળની ત્રિજ્યા કહેવાય.

નોંધઃ રેખાખંડ PA તથા તેની લંબાઈ બંને માટે ત્રિજ્યા શબ્દનો ઉપયોગ થાય છે.

→ વર્તુળ દ્વારા સમતલનું વિભાજન વર્તુળ જે સમતલમાં આવેલું છે તેને ત્રણ ભાગમાં વિભાજિત કરે છે :

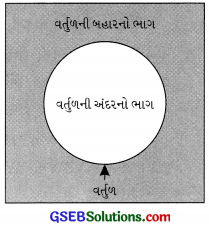
• વર્તુળની અંદરનો વર્તુળની બહારનો ભાગ (Interior of the circle),
• વર્તુળ અને
• વર્તુળની બહારનો વર્તુળની અંદરનો ભાગ (Exterior of the circle).
• વર્તુળ અને તેનો અંદરનો ભાગ મળીને વર્તુળાકાર પ્રદેશ (Circular region) બનાવે છે.

→ વર્તુળની જીવા (Chord of a circle) : વર્તુળ પરનાં કોઈ પણ બે બિંદુને જોડતા રેખાખંડને વર્તુળની જીવા કહે છે. આપેલ આકૃતિમાં AB જીવા છે.

→ વર્તુળનો વ્યાસ (Diameter) : વર્તુળના કેન્દ્રમાંથી પસાર થતી જીવાને વર્તુળનો વ્યાસ કહે છે. આપેલ આકૃતિમાં XY એ વર્તુળનો વ્યાસ છે. ત્રિજ્યાની જેમ જ વ્યાસ શબ્દ પણ રેખાખંડ તેમજ તેની લંબાઈ બંને અર્થમાં વપરાય છે. વ્યાસ એ વર્તુળની મોટામાં મોટી જીવા છે અને બધા વ્યાસની લંબાઈ સરખી હોય છે. તે ત્રિજ્યા કરતાં બમણી હોય છે.

એક વર્તુળનું ચાપ (Arc of a circle) : વર્તુળ પરનાં બે બિંદુઓ વચ્ચેના વર્તુળના ભાગને વર્તુળનું ચાપ કહે છે. આપેલ આકૃતિમાં વર્તુળ પરનાં બે બિંદુઓ P અને દ્વારા વર્તુળના બે ભાગ મળે છે એક મોટો અને એક નાનો. મોટા ભાગને ગુરુચાપ (Major arc) PQ અને નાના ભાગને (Minor arc) PQ કહે છે.

લઘુચાપ PQને \(\widehat{\mathrm{PQ}}\) વડે અને ગુરુચાપ PQ ને જો R એ P તથા 9 વચ્ચેનું ગુરુચાપનું કોઈ બિંદુ હોય, તો \(\widehat{\mathrm{PQR}}\) વડે દર્શાવાય છે.
જો કાંઈ પણ દર્શાવવામાં ન આવ્યું હોય, તો ચાપ PQ અથવા \(\widehat{\mathrm{PQ}}\) ને લઘુચાપ PQ સમજીશું. જ્યારે P અને 9 વ્યાસનાં અંત્યબિંદુઓ હોય, ત્યારે બંને ચાપ સમાન છે અને તેમને અર્ધવર્તુળ (Semicircle) કહે છે.

→ પરિઘ (Circumference) : વર્તુળની પૂર્ણ લંબાઈને વર્તુળનો પરિઘ કહે છે.

→ વૃત્તખંડ (segment): જીવા અને તેનાં બંનેમાંથી કોઈ પણ ચાપ વચ્ચેના પ્રદેશને વર્તુળાકાર પ્રદેશનો વૃત્તખંડ અથવા સરળ રીતે વર્તુળનો વૃત્તખંડ કહે છે.

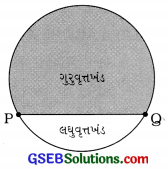
જીવા અને લઘુચાપ વડે બનતા વૃત્તખંડને લઘુત્તખંડ (Minor ગુરુવૃત્તખંડ segment) તથા જીવા અને ગુરુચાપ વડે બનતા વૃત્તખંડને ગુરુવૃત્તખંડ લધુવૃત્તખંડ (Major segment) કહે છે.

→ વૃત્તાંશ (sector): ચાપ અને વર્તુળના કેન્દ્રથી ચાપનાં બંને ગુરુવૃત્તાંશ અંત્યબિંદુઓને જોડતી બે ત્રિજ્યાઓ વચ્ચેના વર્તુળાકાર પ્રદેશના ભાગને વૃત્તાંશ કહે છે. લઘુચાપ અને તેનાં અંત્યબિંદુઓમાંથી દોરેલ P લઘુવૃત્તાંશ ત્રિજ્યાઓ દ્વારા લઘુવૃત્તાંશ (Minor sector) મળે તથા ગુરુચાપ અને તેનાં અંત્યબિંદુઓમાંથી દોરેલ ત્રિજ્યાઓ દ્વારા ગુરુવૃત્તાંશ (Major sector) મળે.

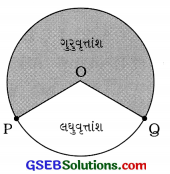
જ્યારે બંને ચાપ સમાન હોય ત્યારે બંને વૃત્તખંડ અને બંને વૃત્તાંશ સમાન હોય છે તથા પ્રત્યેકને અર્ધવૃત્તીય પ્રદેશ (Semicircular region) કહે છે.

→ જીવાએ કોઈ બિંદુ આગળ આંતરેલો ખૂણો:
રેખાખડે બિંદુ આગળ આંતરેલ ખૂણોઃ આપેલ રેખાખંડની બહારના બિંદુને રેખાખંડનાં અંત્યબિંદુઓ સાથે જોડવાથી જે ખૂણો બને તે ખૂણાને આપેલ રેખાખંડે તે બિંદુ આગળ આંતરેલ ખૂણો (Subtended angle) કહે છે.

અહીં, આકૃતિમાં રેખાખંડ ABની બહારનું બિંદુ P છે. PA અને PB દોરવાથી ∠APB મળે છે, જેને રેખાખંડ AB એ P આગળ આંતરેલ ખૂણો કહેવાય.

→ વર્તુળની જીવાએ આંતરેલ ખૂણાઃ 0 કેન્દ્રવાળા વર્તુળમાં AB જીવા છે, P એ ગુરુચાપ AB પરનું બિંદુ છે અને એ લઘુચાપ AB પરનું બિંદુ છે.

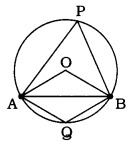
અહીં, ∠AOB એ જીવા AB એ કેન્દ્ર છે આગળ આંતરેલ ખૂણો છે,
∠APB એ જીવા AB એ ગુરુચાપ પરના બિંદુ P આગળ આંતરેલ ખૂણો છે અને ∠AQB એ જીવા AB એ લઘુચાપ પરના બિંદુ Q આગળ આંતરેલ ખૂણો છે.

→ પ્રમેય 10.1 વર્તુળ(એકરૂપ વર્તુળો)ની સમાન જીવાઓ, વર્તુળના કેન્દ્ર (અનુરૂપ કેન્દ્ર) આગળ સમાન ખૂણા અંતરે છે.

→ પ્રમેય 10.2: જો વર્તુળ(સમાન વર્તુળો)ની બે જીવાઓ કેન્દ્ર (અનુરૂપ કેન્દ્ર) આગળ સમાન ખૂણા આંતરે, તો તે જીવાઓ સમાન છે.

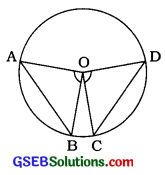
ઉપરોક્ત બંને પ્રમેય એકબીજાના પ્રતીપ છે. જો AB = CD આપેલ હોય, તો ∠AOB = ∠COD સાબિત થાય અને જો ∠AOB = ∠COD આપેલ હોય, તો AB = CD સાબિત થાય.

ઉદાહરણ : 1.
સાબિત કરો કે, વર્તુળની સમાન જીવાઓ વર્તુળના કેન્દ્ર આગળ સમાન ખૂણા અંતરે છે.
ઉત્તર:
પક્ષ: AB અને CD એ O છે કેન્દ્રિત વર્તુળની સમાન જીવાઓ છે, એટલે કે AB = CD.
સાધ્ય ∠AOB = ∠COD

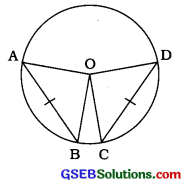
સાબિતી : ∆OAB અને ∆OCDમાં,
OA = OC (એક જ વર્તુળની ત્રિજ્યાઓ)
OB = OD (એક જ વર્તુળની ત્રિજ્યાઓ)
AB = CD (પક્ષ)
∴ ∆OAB ≅ ∆OCD (બાબાબા)
∴ ∠AOB = ∠COD (CPCT)

ઉદાહરણ : 2.
સાબિત કરો કે, જો વર્તુળની બે જીવાઓ વર્તુળના કેન્દ્ર આગળ સમાન ખૂણા આંતરે, તો તે જીવાઓ સમાન છે.
ઉત્તર:
પક્ષઃ O કેન્દ્રિત વર્તુળની જીવાઓ AB અને PQ કેન્દ્ર આગળ સમાન ખૂણા આંતરે છે, એટલે કે ∠AOB = ∠POQ.
સાધ્ય : AB = PQ

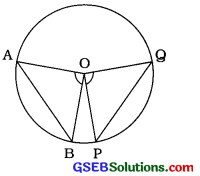
સાબિતી : ∆AOB અને POQમાં,
OA = OP (એક જ વર્તુળની ત્રિજ્યાઓ)
OB = 09 (એક જ વર્તુળની ત્રિજ્યાઓ)
∴ ∠AOB = ∠POQ (પક્ષ)
∴ ∆AOB = ∆POQ (બાખૂબા)
∴ AB = PQ (CPCT)

→ કેન્દ્રમાંથી જીવા પર દોરેલો લંબઃ

• પ્રમેય 10.૩૯ વર્તુળના કેન્દ્રમાંથી જીવા પર દોરેલો લંબ, જીવાને દુભાગે છે.
• પ્રમેય 10.4: વર્તુળના કેન્દ્રમાંથી પસાર થતી રેખા જીવાને દુભાગે, તો તે રેખા જીવાને લંબ છે. ઉપરોક્ત બંને પ્રમેય એકબીજાના પ્રતીપ છે.

→ એક અગત્યનું પરિણામઃ વર્તુળની જીવાનો લંબદ્વિભાજક વર્તુળના કેન્દ્રમાંથી પસાર થાય છે.

→ ત્રણ બિંદુઓમાંથી વર્તુળઃ આપેલ એક બિંદુમાંથી પસાર થતા અસંખ્ય વર્તુળ મળે. તે જ રીતે, આપેલ બે બિંદુમાંથી પસાર થતા અસંખ્ય વર્તુળ મળે.

→ પ્રમેય 10.5 : આપેલ ત્રણ અસમરેખ બિંદુઓમાંથી એક અને માત્ર એક જ વર્તુળ પસાર થાય છે.
નોંધઃ જો ABC એક ત્રિકોણ હોય, તો પ્રમેય 10.5 પ્રમાણે, ત્રિકોણનાં ત્રણ શિરોબિંદુઓ A, B અને Cમાંથી એક અનન્ય વર્તુળ પસાર થાય છે. આ વર્તુળને ∆ABCનું પરિવૃત્ત (Circumcircle) અથવા પરિવર્તુળ કહે છે. તેના કેન્દ્ર અને ત્રિજ્યાને અનુક્રમે ત્રિકોણનું પરિકેન્દ્ર (Circumcentre) અને પરિત્રિજ્યા (Circumradius) કહેવાય છે.

ઉદાહરણ : 1.
O કેન્દ્રિત વર્તુળમાં B જીવા અને BC વ્યાસ છે. oમાંથી જીવા AB પર દોરેલ લંબ AB ને Dમાં છેદે છે. સાબિત કરો કે, CA = 2 OD.
ઉત્તર:

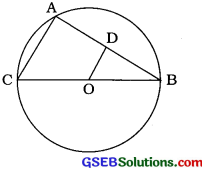
O કેન્દ્રિત વર્તુળમાં BC વ્યાસ છે.
∴ O એ BCનું મધ્યબિંદુ છે.
O કેન્દ્રિત વર્તુળના કેન્દ્ર 0માંથી જીવા AB પર લંબ OD દોરેલ છે. આથી OD એ ABને દુભાગે. (પ્રમેય 10.3)
∴ D એ ABનું મધ્યબિંદુ છે.
આમ, ∆ABCમાં, O એ BCનું અને D એ ABનું મધ્યબિંદુ છે. આથી પ્રમેય 8.9 (મધ્યબિંદુ પ્રમેય) મુજબ,
OD ∥ CA અને OD = \(\frac{1}{2}\) CA
CA = 2OD

→ એક રેખા અને બિંદુ વચ્ચેનું અંતર રેખા AB અને તેની બહારનું બિંદુ P હોય, તો Pમાંથી AB પર દોરેલ લંબ PM મેળવો, જ્યાં M એ ABનું બિંદુ હોય. આ રેખાખંડ PMની લંબાઈને બિંદુ Pનું રેખા ABથી અંતર અથવા રેખા ABનું બિંદુ Pથી અંતર કહે છે. બિંદુ P રેખા AB પર હોય તો તેનું રેખાથી અંતર શૂન્ય થાય.

→ સમાન જીવાઓ અને તેમનું કેન્દ્રથી અંતરઃ
પ્રમેય 10.6 વર્તુળ(અથવા એકરૂપ વર્તુળો)ની સમાન જીવાઓ વર્તુળના કેન્દ્ર(કેન્દ્રો)થી સમાન અંતરે આવેલી હોય છે.

→ પ્રમેય 10.7: વર્તુળ(એકરૂપ વર્તુળ)ના કેન્દ્ર અનુરૂપ કેન્દ્ર)થી સમાન અંતરે આવેલી જીવાઓ સમાન હોય છે.

ઉદાહરણ : 1.
P કેન્દ્રિત વર્તુળની ત્રિજ્યા 20 સેમી છે. AB એ રે કેન્દ્રિત વર્તુળની એક જીવા છે. જો AB = 32 સેમી હોય, તો ABનું P થી અંતર શોધો.
ઉત્તર:

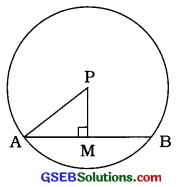
ત્રિજ્યા PA તથા PM ⊥ AB દોરો.
∴ M એ ABનું મધ્યબિંદુ છે. (પ્રમેય 10.3) .
∴ MA = AB = 2 × 32 સેમી = 16 સેમી
PA એ વર્તુળની ત્રિજ્યા છે.
∴ PA = 20 સેમી

∆PMAમાં, ∠M = 90°
∴ PA² = PM² + MA² (પાયથાગોરસ પ્રમેય)
∴ PM² = PA² – MA²
= (20)² – (16)²
= 400 – 256
= 144
∴ PM = \(\sqrt{144}\) = 12 સેમી
આમ, ABનું Pથી અંતર 12 સેમી છે.

ઉદાહરણ : 2.
એક વિહારસ્થાનમાં 5 મી ત્રિજ્યાવાળા દોરેલા વર્તુળ પર રમત રમવા માટે ત્રણ છોકરીઓ રેશ્મા, સલમા અને મનદીપ ઊભાં છે. રેશ્મા દડાને સલમા તરફ ફેકે છે. સલમા મનદીપ તરફ અને મનદીપ રેશ્મા તરફ દડો ફેકે છે. જો રેશ્મા અને સલમા વચ્ચેનું તથા સલમા અને મનદીપ વચ્ચેનું દરેક અંતર 6 મીટર હોય, તો રેશ્મા અને મનદીપ વચ્ચેનું અંતર કેટલું હશે?
ઉત્તર:
અહીં દર્શાવેલ વર્તુળ પર R, S અને M અનુક્રમે રેશમા, સલમા અને મનદીપનાં સ્થાન દર્શાવે છે.

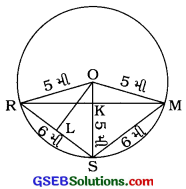
આથી OR = OM = OS = 5 મીટર (વર્તુળની ત્રિજ્યા)
તથા RS = SM = 6 મીટર
ચતુષ્કોણ ORSMમાં OR = OM = 5 મી અને
RS = SM = 6 મી માટે,
ચતુષ્કોણ ORSM પતંગાકાર છે.
આથી તેનો વિકર્ણ OS એ વિકર્ણ Rખને કાટખૂણે દુભાગે છે.
∴ ∠RKO = 90° ……. (1)
વર્તુળના કેન્દ્ર 0માંથી જીવા RM પર લંબ OK છે. માટે, K એ RMનું મધ્યબિંદુ છે.
∴ RM = 2RK … (2)
કેન્દ્ર 0માંથી જીવા RS પર લંબ OL દોરો.

∴ RL = \(\frac{1}{2}\)RS = \(\frac{1}{2}\) × 6 = 3 મી
∆RLOમાં, ∠L = 90°
∴ RO² = OL² + RL²
∴ 5² = OL² + 3².
∴ 25 = OL² + 9.
∴ OL² = 16
∴ OL = 4 મી

હવે, A ROSનું ક્ષેત્રફળ = \(\frac{1}{2}\) × RS × OL
= \(\frac{1}{2}\) × OS × RK [(1) પરથી],
∴ RS × OL = OS × RK
∴ 6 × 4 = 5 × RK
∴ 24 = 5 × RK
∴ RK = \(\frac{24}{5}\) = 4.8મી

વળી, RM = 2RK [(2) મુજબ]
∴ RM = 2 × 4.8
RM = 9.6 મી
આમ, રેશ્મા અને મનદીપ વચ્ચેનું અંતર 9.6 મી થાય.

ઉદાહરણ : 3.
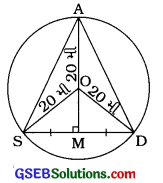
એક વસાહતમાં 20 મીટર ત્રિજ્યાવાળું એક વર્તુળાકાર વિહારસ્થાન આવેલું છે. ત્રણ છોકરાઓ અંકુર, સૈયદ અને ડેવિડ દરેક પોતાના હાથમાં રમકડાનો ટેલિફોન એકબીજા સાથે વાત કરવા માટે રાખીને વર્તુળની સીમા પર સરખા અંતરે બેઠા છે. દરેકના ટેલિફોનની દોરીની લંબાઈ શોધો.

ઉત્તર:
O કેન્દ્રિત વર્તુળ એ વિહારસ્થાન દર્શાવે છે તથા A, S અને D અનુક્રમે અંકુર, સૈયદ અને ડેવિડના સ્થાન દર્શાવે છે. અંકુર, સૈયદ અને ડેવિડ સરખા અંતરે બેઠા હોવાથી ∆ASD સમબાજુ ત્રિકોણ છે. SDના મધ્યબિંદુ Mમાંથી તેનો લંબદ્વિભાજક દોરતાં તે છે અને A બંનેમાંથી પસાર થાય. ધારો કે, SM = x મી

SD = 2SM = 2x મી
સમબાજુ ∆ASDનું ક્ષેત્રફળ = \(\frac{\sqrt{3}}{4}\)(બાજુ)²
સમબાજુ ∆ASDનું ક્ષેત્રફળ = \(\frac{\sqrt{3}}{4}\) × (2x)²
સમબાજુ ∆ASDનું ક્ષેત્રફળ = √3x² ……. (1)
કાટકોણ ∆OMSમાં ∠M = 90°
∴ OM² = OS² – SM² = (20)² – (x)² = 400 – x²

∴OM = \(\sqrt{400-x^{2}}\)
હવે, ∆OSDનું ક્ષેત્રફળ = \(\frac{1}{2}\) × SD × OM .
∆OSDનું ક્ષેત્રફળ = \(\frac{1}{2}\) × 21 × \(\sqrt{400-x^{2}}\)
∆OSDનું ક્ષેત્રફળ= x\(\sqrt{400-x^{2}}\) …… (2)
અહીં, ∆OAS, ∆OSD અને ∆ODA એકરૂપ ત્રિકોણો છે.
∆ASDનું ક્ષેત્રફળ = ∆OASનું ક્ષેત્રફળ + ∆OSDનું ક્ષેત્રફળ + ∆ODAનું ક્ષેત્રફળ .
∆ASDનું ક્ષેત્રફળ = 3 × ∆OSDનું ક્ષેત્રફળ
√3 x² = 3 × x \(\sqrt{400-x^{2}}\)
x² = 3(400 – x²)
x² = 3(400 – x²).
4x² = 1200 – 3x²
4x = 1200
x² = 300
x = 10√3
SD = 2x = 2 × 10√3 = 20√3
આમ, દરેકના ટેલિફોનની દોરીની લંબાઈ 20√3મી થાય.

→ વર્તુળના ચાપે આંતરેલો ખૂણો:

• જો વર્તુળની બે જીવા સમાન હોય, તો તેમને અનુરૂપ ચાપ એકરૂપ છે.
• જો વર્તુળના બે ચાપ એકરૂપ હોય, તો તેમને અનુરૂપ જીવા સમાન છે.

→ વર્તુળના ચાપે કેન્દ્ર આગળ આંતરેલો ખૂણોઃ વર્તુળના ચારે કેન્દ્ર આગળ આંતરેલો ખૂણો એટલે તે ચાપની અનુરૂપ જીવાએ કેન્દ્ર આગળ આંતરેલો ખૂણો. લઘુચાપ AB કેન્દ્ર આગળ લઘુકોણ ∠AOB આંતરે છે અને ગુરુચાપ AB કેન્દ્ર આગળ વિપરીતકોણ ∠AOB આંતરે છે.

→ વર્તુળના એકરૂપ ચાપ અથવા સમાન લંબાઈના ચાપ કેન્દ્ર આગળ સમાન ખૂણા અંતરે છે.

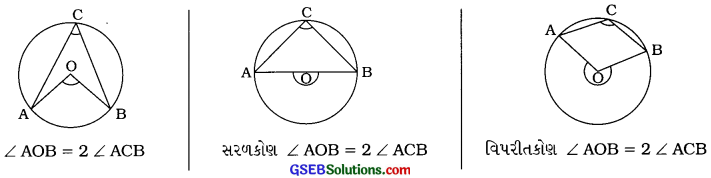
→ પ્રમેય 10.8: વર્તુળના ચારે કેન્દ્ર આગળ આંતરેલો ખૂણો તે ચાપે વર્તુળના બાકીના ભાગ પરના કોઈ પણ બિંદુ આગળ આંતરેલા ખૂણા કરતાં બમણો હોય છે.

નોંધઃ અર્ધવર્તુળમાંનો ખૂણો કાટખૂણો હોય છે.

→ પ્રમેય 10.9: એક જ વૃત્તખંડમાં આવેલા ખૂણાઓ સમાન

→ પ્રમેય 10.10: જો બે બિંદુઓને જોડતો રેખાખંડ, એ રેખાખંડને સમાવતી રેખાની એક જ બાજુએ આવેલાં બીજાં બે બિંદુઓ આગળ સમાન ખૂણા આંતરે, તો ચારેય બિંદુઓ એક જ વર્તુળ પર આવેલાં છે. (આ ચારેય બિંદુઓ વૃત્તીય (Concyclic) બિંદુઓ કહેવાય.)

→ ચક્રીય (Cyclic) ચતુષ્કોણ જે ચતુષ્કોણનાં બધાં જ હોય છે. શિરોબિંદુઓ એક જ વર્તુળ પર આવેલાં હોય તે ચતુષ્કોણને ચક્રીય ચતુષ્કોણ કહે છે.

→ પ્રમેય 10.11: ચક્રીય ચતુષ્કોણના સામસામેના ખૂણાઓની પ્રત્યેક જોડના ખૂણાઓનો સરવાળો 180° થાય છે.

→ પ્રમેય 10.12: જો ચતુષ્કોણના સામસામેના ખૂણાઓની જોડના ખૂણાઓનો સરવાળો 180° હોય, તો તે ચતુષ્કોણ ચક્રીય ∠AXB = ∠AYB ચતુષ્કોણ છે.
આમ, જો ચતુષ્કોણ ABCD એ ચક્રીય ચતુષ્કોણ હોય, તો ∠A + ∠C = ∠B+ ∠D = 180° અને જો ચતુષ્કોણ ABCDમાં ∠A + ∠C = ∠B + ∠D = 180° હોય, તો ABCD ચક્રીય ચતુષ્કોણ છે.

નોંધઃ ∠A + ∠C = 180° પરથી ∠B + ∠D = 180° આપોઆપ મળે.

ઉદાહરણ : 1.
P કેન્દ્રિત વર્તુળમાં AB જીવા છે. બિંદુ C એ ગુરુચાપ AB પરનું A અને Bથી ભિન્ન બિંદુ છે. નીચેના પ્રશ્નોના જવાબ આપો :
(1) જો ∠ACB = 50° હોય, તો ∠APB શોધો.
(2) જો ∠APB = 180° હોય, તો ∠ACH શોધો.
(૩) જો ∠ACB + ∠APB = 135 હોય, તો ∠ACE અને ∠APB શોધો.
ઉત્તર:

P કેન્દ્રિત વર્તુળમાં AB જીવા છે અને બિંદુ C એ ગુરુચાપ AB પરનું A અને Bથી ભિન્ન બિંદુ છે.
∠APB = 2∠ACB

(1) અહીં, ∠ACB = 50°
∠APB = 2 ∠ACB = 2 × 50 = 100°

(2) અહીં, ∠APB = 130°
∠APB = 2 ∠ACB
∠ACB = ∠APB = 2 × 130° = 65°

(3) ∠ACB + ∠APB = 135°
∠ACB + 2 ∠ACB = 135° (∵ ∠APB = 2 ∠ACB)
3∠ACB = 135°
∠ACB = \(\frac{135°}{3}\)
∠ ACB = 45°
હવે, ∠APB = 2 ∠ACB = 2 × 45 = 90°

ઉદાહરણ : 2.
આપેલ આકૃતિમાં ચક્રીય ચતુષ્કોણ ABCDના વિકર્ણો બિંદુ માં છે છેદે છે. જો ∠BAC = 50° અને ∠ADB = 45° હોય, તો ∠ABC શોધો.
ઉત્તર:

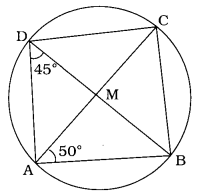
∠BDC = ∠BAC (એક જ વૃત્તખંડના ખૂણા)
∠BDC = 50° (∵ ∠BAC = 50°).

હવે, ∠ADC = ∠ADB + ∠BDC (આસન્નકોણ)
∠ADC = 45° + 50° .
∠ADC = 95°
ચતુષ્કોણ ABCD ચક્રીય ચતુષ્કોણ છે.
∠ ABC + ∠ADC = 180°
∠ABC + 95° = 180°
∠ABC = 180° – 95°
∠ABC = 85°

ઉદાહરણ : 3.
જો ત્રિકોણની બે બાજુઓ વ્યાસ થાય તેવી રીતે વર્તુળો દોરેલાં હોય, તો સાબિત કરો કે, આ વર્તુળોનું એક છેદબિંદુ, ત્રિકોણની ત્રીજી બાજુ પર આવેલું છે.

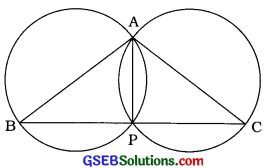
ઉત્તર:
∆ABCની બાજુઓ AB અને AC વ્યાસ થાય તે રીતે વર્તુળો દોરેલ છે જે એકબીજાને A અને P બિંદુમાં છેદે છે. સામાન્ય જીવા AP દોરો.
AB વ્યાસ હોવાથી ∠APB અર્ધવર્તુળે આંતરેલો ખૂણો છે.
∴ ∠APB = 90°

AC વ્યાસ હોવાથી ∠APC અર્ધવર્તુળ આંતરેલો ખૂણો છે.
∴ ∠APC = 90°

આથી ∠APB + ∠APC = 90° + 90° = 180°
∴ ∠APB અને ∠APC સામાન્ય ભુજ AP ધરાવતા આસન્નકોણ છે અને તેમનો સરવાળો 180° છે.

∴ ∠APB અને ∠APC રેખિક જોડના ખૂણા છે.
∴ બિંદુ એ AABCની ત્રીજી બાજુ BC પર આવેલું છે.

ઉદાહરણ : 4.
ત્રિકોણ ABCના ખૂણાઓ A, B અને Cના દુભાજકો, ત્રિકોણના પરિવર્તુળને અનુક્રમે D, E અને Fમાં છેદે છે. સાબિત કરો કે, ત્રિકોણ DEના ખૂણાઓ 90° – \(\frac{1}{2}\)A, 90° – \(\frac{1}{2}\)B અને 90° – \(\frac{1}{2}\)C છે.

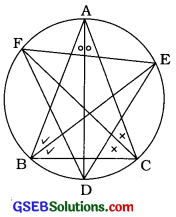
ઉત્તર:
∆ABCના ખૂણાઓ A, B અને Cના દ્વિભાજકો તેના પરિવૃત્તને અનુક્રમે D, E અને Fમાં છેદે છે.

∠FDE = ∠FDA + ∠EDA (આસન્નકોણ)
= ∠FCA + ∠EBA (એક જ વૃત્તખંડના ખૂણા)
= \(\frac{1}{2}\)∠C + \(\frac{1}{2}\)∠B (A ABCના કોણ દ્વિભાજકો)
= \(\frac{1}{2}\)(∠B + ∠C)
= \(\frac{1}{2}\)(180° – ∠A) [∠A + ∠B+ ∠C = 180°]
= 90° – ∠A

આમ, ∠FDE = 90° – \(\frac{1}{2}\)∠A મળે.
તે જ રીતે, ૮DEF = 90° – \(\frac{1}{2}\)∠B અને
∠EFD = 90°– \(\frac{1}{2}\)∠C મળે.