GSEB Class 9 Maths Notes Chapter 15 સંભાવના

This GSEB Class 9 Maths Notes Chapter 15 સંભાવના covers all the important topics and concepts as mentioned in the chapter.

સંભાવના Class 9 GSEB Notes

→ આપણે સામાન્ય બોલચાલની ભાષામાં “સંભાવના’, ‘તક’, ‘મોટે ભાગે’, “શક્યતા છે’ વગેરે શબ્દોનો ઉપયોગ કરીએ છીએ.

→ આપણા રોજિંદા જીવનમાં કેટલીક ચોક્કસ ઘટનાઓ જોવા મળે છે, જેનું આપણે ચોક્કસ અનુમાન કરી શકીએ છીએ. દા. ત., સૂર્યનું પૂર્વ દિશામાં ઊગવું, ઊર્ધ્વદિશામાં ફેકેલી વસ્તુનું પૃથ્વી પર નીચે પડવું વગેરે. પરંતુ કેટલીક ઘટનાઓ એવી છે કે જેનો પ્રયત્ન હાથ ધરવામાં આવે ત્યારે જ તેના શક્ય બધાં પરિણામો વિશે જાણીએ છીએ, પરંતુ આપણે તેના આવનારા સાચા પરિણામ વિશે ચોક્કસ અનુમાન કે આગાહી કરી શક્તા નથી. આ ચોક્કસ પરિસ્થિતિમાં ચોક્કસતાનું વિશ્લેષણ મેળવવાનો ગાણિતિક અભ્યાસ એટલે સંભાવના.

→ 17મી સદીમાં ફ્રેન્ચ ગણિતશાસ્ત્રી પાસ્કલને અને ફર્માને સંભાવના વિશેનો વિચાર સ્ફર્યો. શરૂઆતમાં જુગારની રમતમાં શક્યતાઓ વિચારવા માટે સંભાવનાનો ઉપયોગ થવા લાગ્યો. પાછળથી તેનો પૂર્ણપણે ગાણિતિક સ્વરૂપમાં વિકાસ થયો. હાલમાં સંભાવનાનો ઉપયોગ અનેકવિધ શાખાઓમાં થાય છે.

→ જ્યારે પ્રયત્નોનાં પરિણામ સીધા જોઈ શકતા હોઈએ ત્યારે આપણને પ્રાયોગિક અથવા આનુભાવિક સંભાવના મળે, આપણે સરળતા ખાતર પ્રાયોગિક સંભાવનાને બદલે ફક્ત સંભાવના જ લખીશું.

→ પ્રયત્ન: પ્રયત્ન એ એક ક્રિયા છે, જેમાં એક કે તેથી વધુ પરિણામ મળી શકે છે.

→ ઘટના (Event): પ્રયોગ માટેની ઘટના એ પ્રયોગનાં કેટલાંક પરિણામોનું એકત્રીકરણ છે. ઘટનાને સામાન્ય રીતે A, B, C, … વગેરે વડે દર્શાવાય છે.

→ નિવારક ઘટનાઓ ઘટનાઓ A અને B માટે જો A અને B માટે કોઈ પણ પરિણામ સામાન્ય ન હોય, તો ઘટનાઓ A અને B પરસ્પર નિવારક ઘટનાઓ છે તેમ કહેવાય.

→ સંભાવના (Probability): કોઈ ઘટનાની સંભાવના એટલે તે ઘટના માટેના પ્રયત્નોની સંખ્યા અને પ્રયોગના પ્રયત્નોની કુલ સંખ્યાઓનો ગુણોત્તર.
ઘટના A બને તેની સંભાવનાને P(A) વડે દર્શાવાય છે.

→ સંભાવનાના ગુણધર્મો :

• કોઈ પણ ઘટનાની સંભાવના 0, 1 કે તેમની વચ્ચેની કોઈ પણ વાસ્તવિક સંખ્યા છે.
  તેથી કોઈ ઘટના A માટે 0 ≤ P (A) ≤ 1.
• બધી જ પરસ્પર નિવારક ઘટનાઓની સંભાવનાઓનો સરવાળો 1 છે.
• અશક્ય ઘટનાની સંભાવના 0 છે અને નિશ્ચિત (ચોક્કસ) ઘટનાની સંભાવના 1 છે.

ઉદાહરણ : 1.
ત્રણ સિક્કા એકસાથે 500 વખત ઉછાળવાના પ્રયોગમાં મળતી છાપની સંખ્યા નીચેના કોષ્ટકમાં નોંધેલ છેઃ

છાપની સંખ્યા 0, 1, 2 અથવા ૩ આવે તે દરેક ઘટનાની સંભાવના શોધો. ચકાસો કે તે બધી જ સંભાવનાઓનો સરવાળો 1 થાય છે.
ઉત્તર:
ત્રણ સિક્કા એકસાથે ઉછાળવાના પ્રયોગમાં 0 છાપ મળે, 1 છાપ મળે, 2 છાપ મળે અને 3 છાપ મળે તે ઘટનાઓને અનુક્રમે A₁, A₂, A₃ અને A₄ વડે દર્શાવીએ, તો
P (A₁) = \(\frac{70}{500}\) = 0.14
P(A₂) = \(\frac{190}{500}\) = 0.38
P (A₃) = \(\frac{175}{500}\) = 0.35
P (A₄) = \(\frac{65}{500}\) = 0.13
અહીં, P (A₁) + P (A₂) + P (A₃) + P (A₄)
= 0.14 + 0.38 + 0.35 + 0.13
= 1

ઉદાહરણ : 2.
એક પાસો 400 વખત ફેંકવામાં આવે છે. પાસા પર 1, 2, 3, 4, 5 અને 6 મળે તેની આવૃત્તિઓ નીચેના કોષ્ટકમાં દર્શાવેલ છે

દરેક પરિણામ આવવાની સંભાવના શોધો.
ઉત્તર:
પાસા પર આવતા પરિણામ 1, 2, 3, 4, 5, 6ને અનુક્રમે ઘટના A₁ A₂ A₃ A₄, A₅, A₆ તરીકે દર્શાવીએ, તો
P (A₁) = \(\frac{68}{400}\) = = 0.17
P (A₂) = \(\frac{70}{400}\) = 0.175
P (A₃) = \(\frac{74}{400}\) = 0.185
P (A₄) = \(\frac{54}{400}\) = 0.135
P (A₅) = \(\frac{70}{400}\) = 0.175
P (A₆) = \(\frac{64}{400}\)= 0.16

ઉદાહરણ : 3.
એક કારખાનાના 100 કર્મચારીઓના ટેલિફોન નંબરની યાદી પરથી તે નંબરના એકમના સ્થાનમાં આવતા અંક મુજબ નીચેનું આવૃત્તિ, વિતરણ મળે છે:

કોઈ એક કર્મચારીને યાદચ્છિક રીતે પસંદ કરવામાં આવે તો તેના ટેલિફોન નંબરમાં એકમનો અંક 3 હોય તેની સંભાવના શોધો.
ઉત્તર:

= \(\frac{15}{100}\) = 0.15

ઉદાહરણ : 4.
શહેરના એક મંદિરની સામેથી એક કલાક દરમિયાન પસાર થતાં ? વાહનોની માહિતી નીચે મુજબ છે :

હવે પછી મંદિરની સામેથી પસાર થતું વાહન દ્વિચક્રી વાહન હોય તેની સંભાવના શોધો.
ઉત્તર:
મંદિર સામેથી પસાર થતાં કુલ વાહનોની સંખ્યા = 90 + 35 + 25
= 150
હવે પછી પસાર થતું વાહન દ્વિચક્રી હોય તેની સંભાવના

ઉદાહરણ : 5.
2 સંતાન ધરાવતાં 1000 કુટુંબોમાં દીકરીની સંખ્યાની માહિતી નીચે મુજબ મળે છેઃ

દીકરીની સંખ્યા	કુટુંબોની સંખ્યા
0	128
1	672
2	200

કોઈ એક કુટુંબ યાદચ્છિક રીતે પસંદ કરતાં તે કુટુંબમાં
(1) બે દીકરીઓ હોય,
ઉત્તર:
બે દીકરીઓ હોય તેવાં કુટુંબોની સંખ્યા = 200
કુલ કુટુંબોની સંખ્યા = 1000
∴ પસંદ કરેલ કુટુંબમાં બે દીકરીઓ હોય તેની સંભાવના
= \(\frac{200}{1000}\)
= 0.2

(2) એક દીકરી હોય તેની સંભાવના શોધો.
ઉત્તર:
એક દીકરી હોય તેવાં કુટુંબોની સંખ્યા = 672
કુલ કુટુંબોની સંખ્યા = 1000
∴ પસંદ કરેલ કુટુંબમાં એક દીકરી હોય તેની સંભાવના
= \(\frac{672}{1000}\) = 0.672

ઉદાહરણ : 6.
કોઈ એક શહેરમાં એક વીમાકંપનીએ 1600 ડ્રાઇવરની પસંદગી કરી. તેમની ઉંમર અને તેમણે એક વર્ષમાં કરેલ અકસ્માત વચ્ચેનો સંબંધ શોધવા નીચે મુજબનું કોષ્ટક બનાવ્યું:

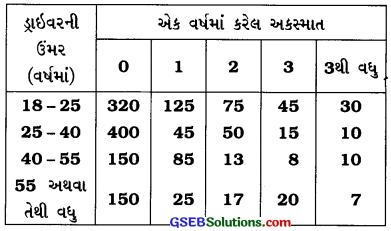
એક ડ્રાઇવરને યાદચ્છિક રીતે પસંદ કરતાં તે 25-40 વર્ષના જથનો હોય અને તેણે વર્ષમાં 2 અકસ્માત કર્યા હોય તેની સંભાવના શોધો.
ઉત્તર:
25 – 40 વર્ષના જૂથનો હોય અને તેણે વર્ષમાં 2 અકસ્માત કર્યા હોય તેવા ડ્રાઇવરોની સંખ્યા = 50
કુલ ડ્રાઇવરોની સંખ્યા = 1600
∴ પસંદ કરેલ ડ્રાઇવર 25 – 40 વર્ષના જૂથનો હોય અને તેણે વર્ષમાં 2 અકસ્માત કર્યા હોય તેની સંભાવના
= \(\frac{50}{1600}\)
= \(\frac{1}{32}\)