GSEB Solutions Class 8 Maths Chapter 11 માપન Ex 11.4

Gujarat Board GSEB Solutions Class 8 Maths Chapter 11 માપન Ex 11.4 Textbook Exercise Questions and Answers.

Gujarat Board Textbook Solutions Class 8 Maths Chapter 11 માપન Ex 11.4

પ્રશ્ન 1.
તમને એક નળાકાર ટાંકી આપેલ છે. નીચે આપેલી કઈ પરિસ્થિતિમાં તમે તેનું પૃષ્ઠફળ મેળવશો અને કઈ પરિસ્થિતિમાં તેનું ઘનફળ મેળવશો?

પ્રશ્ન (i)
નળાકાર ટાંકીમાં કેટલું પાણી રાખી શકાશે, તે નક્કી કરવા માટે.
ઉત્તરઃ
નળાકાર ટાંકીમાં કેટલું પાણી રાખી શકાશે, તે નક્કી કરવા માટે નળાકાર ટાંકીનું ઘનફળ મેળવીશું.

પ્રશ્ન (ii)
નળાકાર ટાંકીને પ્લાસ્ટર કરવા માટે જરૂરી સિમેન્ટની થેલીઓની સંખ્યા જાણવા.
ઉત્તરઃ
નળાકાર ટાંકીને પ્લાસ્ટર કરવા માટે જરૂરી સિમેન્ટની થેલીઓની સંખ્યા જાણવા માટે નળાકાર ટાંકીનું પૃષ્ઠફળ મેળવીશું.

પ્રશ્ન (iii)
નળાકાર ટાંકીમાં ભરેલા પાણીથી પાણીની કેટલી નાની ટાંકીઓ ભરાશે તેની સંખ્યા જાણવાં.
ઉત્તરઃ
નળાકાર ટાંકીમાં ભરેલા પાણીથી પાણીની કેટલી નાની ટાંકીઓ ભરાશે તેની સંખ્યા જાણવા નળાકાર ટાંકીનું ઘનફળ મેળવીશું.

પ્રશ્ન 2.
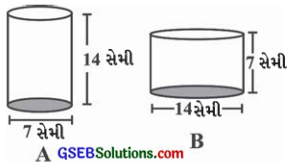
નળાકાર થનો વ્યાસ 7 સેમી અને ઊંચાઈ 14 સેમી છે. નળાકાર Bનો વ્યાસ 14 સેમી અને ઊંચાઈ 7 સેમી છે. ગણતરી કર્યા વગર તમે કહી શકશો કે ઉપરના બે નળાકારમાંથી કોનું ઘનફળ વધારે હશે? બંને નળાકારનું ઘનફળ મેળવી તમારા જવાબને ચકાસો. આ ઉપરાંત એ પણ ચકાસો કે વધુ ઘનફળ ધરાવતા નળાકારનું પૃષ્ઠફળ પણ વધારે છે?

ઉત્તરઃ
બંને નળાકાર જોતાં જણાય છે કે નળાકાર Aની ત્રિજ્યા કરતાં નળાકાર Bની ત્રિજ્યા બેગણી છે.
∴ નળાકાર નું ઘનફળ એ નળાકાર Aના ઘનફળ કરતાં વધારે હોય.
નળાકાર Aનું ઘનફળઃ
નળાકારની ત્રિજ્યા (r) = \(\frac {વ્યાસ}{2}\) = \(\frac {7}{2}\) સેમી અને ઊંચાઈ (h) = 14 સેમી
નળાકાર Aનું ઘનફળ = πr²h = \(\frac {22}{7}\) × (\(\frac {7}{2}\))² × 14
= \(\frac {22}{7}\) × \(\frac {7}{2}\) × \(\frac {7}{2}\) × 14
= 11 × 7 × 7
= 539 સેમી³

નળાકાર Bનું ઘનફળઃ

નળાકારની ત્રિજ્યા (r) = \(\frac {વ્યાસ}{2}\) = \(\frac {14}{2}\) = 7 સેમી અને
ઊંચાઈ (h) = 7 સેમી
નળાકાર Bનું ઘનફળ = πr²h
= \(\frac {22}{7}\) × 7² × 7
= \(\frac {22}{7}\) × 7 × 7 × 7
= 22 × 7 × 7
= 1078 સેમી³

નળાકાર Aનું પૃષ્ઠફળ:

નળાકારની ત્રિજ્યા (r) = \(\frac {7}{2}\) સેમી, ઊંચાઈ (h) = 14 સેમી
નળાકાર Aનું પૃષ્ઠફળ = 2πr(r + h)
= 2 × \(\frac {22}{7}\) × \(\frac {7}{2}\) × (\(\frac {7}{2}\) + 14)
= 22(\(\frac {35}{2}\))
= 11 × 35.
= 385 સેમી²

નળાકાર Bનું પૃષ્ઠફળઃ

નળાકારની ત્રિજ્યા (r) = 7 સેમી, ઊંચાઈ (h) = 7 સેમી
નળાકાર Bનું પૃષ્ઠફળ = 2πr (r + h)
= 2 × \(\frac {22}{7}\) × 7(7 + 7)
= 44 (14)
= 616 સેમી²
આમ, વધુ ઘનફળ ધરાવતા નળાકાર (B)નું પૃષ્ઠફળ પણ વધારે છે.

પ્રશ્ન 3.
એક લંબઘનના આધારનું ક્ષેત્રફળ 180 સેમી² છે અને તેનું ઘનફળ 900 સેમી³ છે, તો તે લંબઘનની ઊંચાઈ શોધો.
ઉત્તરઃ
ધારો કે લંબઘનની ઊંચાઈ h સેમી છે.
હવે, લંબઘનનું ઘનફળ = આધારનું ક્ષેત્રફળ × ઊંચાઈ
∴ 900 = 180 × h
∴ h = \(\frac {900}{180}\) = 5 સેમી
લંબઘનની ઊંચાઈ 5 સેમી છે.

પ્રશ્ન 4.
એક લંબઘન બૉક્સનું માપ 60 સેમી × 54 સેમી × 30 સેમી છે. આ લંબઘન બૉક્સની અંદર 6 સેમી બાજુવાળા કેટલા નાના સમઘન રાખી શકાશે?
ઉત્તરઃ
અહીં લંબઘન બૉક્સની લંબાઈ (l) = 60 સેમી, પહોળાઈ (h) = 54
સેમી અને ઊંચાઈ (h) = 30 સેમી છે.
લંબઘન બૉક્સનું ઘનફળ = લંબાઈ × પહોળાઈ × ઊંચાઈ
= 60 × 54 × 30 સેમી³
સમઘનની બાજુની લંબાઈ (l) = 6 સેમી
સમઘનનું ઘનફળ = (લંબાઈ)³
= (6)³
= 6 × 6 × 6 સેમી³
લંબઘન બૉક્સમાં ગોઠવાતા ઘન = લંબઘનનું ઘનફળ / એક નાના સમઘનનું ઘનફળ
= \(\frac{60 \times 54 \times 30}{6 \times 6 \times 6}\)
= 10 × 9 × 5 = 450
લંબઘન બૉક્સમાં 450 નાના સમઘન રાખી શકાય.

પ્રશ્ન 5.
જેનું ઘનફળ 1.54 મી³ અને તેના આધારનો વ્યાસ 140 સેમી હોય એવા નળાકારની ઊંચાઈ મેળવો.
ઉત્તરઃ
અહીં નળાકારનું ઘનફળ 1.54 મી³ અને આધારનો વ્યાસ 140 સેમી આપેલ છે.
∴ પાયાની ત્રિજ્યા = \(\frac {વ્યાસ }{2}\) = \(\frac {140}{2}\) = 70 સેમી
નળાકારનું ઘનફળ મી³માં છે તેને સેમી³માં ફેરવીએ.
નળાકારનું ઘનફળ = 1.54 મી³
= 1.54 × 100 × 100 × 100
= 15,40,000 સેમી³
નળાકારનું ઘનફળ = πr²h
∴ 15,40,000 = \(\frac {22}{7}\) × 70 × 70 × h
∴ 15,40,000 = 22 × 70 × 10 × h
∴ h = \(\frac{1540000}{22 \times 70 \times 10}\)
∴ h = 100 સેમી = 1 મીટર
આમ, નળાકારની ઊંચાઈ 1 મીટર છે.

પ્રશ્ન 6.
એક દૂધનું ટેન્કર નળાકાર છે, જેની ત્રિજ્યા 1.5 મીટર અને લંબાઈ 7 મીટર છે. આ ટેન્કરમાં કેટલા લિટર દૂધ ભરી શકાશે?
ઉત્તરઃ
દૂધનું ટેન્કર નળાકાર છે.
દૂધના ટૅન્કરની ત્રિજ્યા = 1.5 મી = \(\frac {15}{10}\) મી
દૂધના ટૅન્કરની ઊંચાઈ = 7 મી
દૂધના ટેન્કરનું ઘનફળ = πr²h
= \(\frac {22}{7}\) × (\(\frac {15}{10}\))² × 7
= \(\frac {22}{7}\) × \(\frac {15}{10}\) × \(\frac {15}{10}\) × 7
= \(\frac{11 \times 3 \times 3}{2}\) = \(\frac {99}{2}\) = 49.5 મી³
1 ઘન મીટર = 1000 લિટર
∴ 49.5 ઘન મીટર = 49,500 લિટર
આમ, દૂધના ટેન્કરમાં 49,500 લિટર દૂધ ભરી શકાશે.

પ્રશ્ન 7.
જો કોઈ ઘનની દરેક બાજુને બમણી કરી દેવામાં આવે તો –

પ્રશ્ન (i)
તેના પૃષ્ઠફળમાં કેટલા ગણો વધારો થશે?
ઉત્તરઃ
ધારો કે ઘનની બાજુની લંબાઈ x છે.
આ લંબાઈ બમણી કરતાં ઘનની નવી લંબાઈ = 2x
મૂળ ઘનનું પૃષ્ઠફળ 6l² = 6 × x² = 6x²
નવા ઘનનું પૃષ્ઠફળ = 6l² = 6 × (2x)² = 6 × (4x)² = 24x²
હવે, નવા ઘનનું પૃષ્ઠફળ / મૂળ ઘનનું પૃષ્ઠફળ = \(\frac{24 x^{2}}{6 x^{2}}\) = 4
આમ, પૃષ્ઠફળમાં 4 ગણો વધારો થાય.

પ્રશ્ન (ii)
તેના ઘનફળમાં કેટલા ગણો વધારો થશે?
ઉત્તરઃ
ધારો કે ઘનની બાજુની લંબાઈ x છે.
આ લંબાઈ બમણી કરતાં ઘનની નવી લંબાઈ 2x થાય.
મૂળ ઘનનું ઘનફળ = l³ = x³
નવા ઘનનું ઘનફળ = l³ = (2x)³ = 8x³
હવે, નવા ઘનનું પૃષ્ઠફળ / મૂળ ઘનનું પૃષ્ઠફળ = \(\frac{8 x^{3}}{x^{3}}\) = 8
આમ, ઘનફળમાં 8 ગણો વધારો થાય.

પ્રશ્ન 8.
એક કુંડની અંદર 60 લિટર પાણી પ્રતિ મિનિટના દરથી પડે છે. જો કુંડનું ઘનફળ 108 મી³ હોય, તો આ કુંડને પાણીથી સંપૂર્ણ ભરાતાં કેટલા કલાક લાગશે?
ઉત્તરઃ
કુંડનું ઘનફળ 108 મી³ છે.
1 ઘન મીટર = 1000 લિટર
∴ 108 ઘન મીટર = 1,08,000 લિટર
કુંડમાં 1 મિનિટમાં પડતું પાણી = 60 લિટર
∴ કુંડમાં 1 કલાકમાં પડતું પાણી = 60 × 60 લિટર
∴ કુંડને પાણીથી ભરાતાં લાગતો સમય = \(\frac{108000}{60 \times 60}\) = 30 કલાક
∴ કુંડને પાણીથી ભરાતાં સંપૂર્ણ 30 કલાક લાગશે.