Gujarat Board GSEB Solutions Class 10 Maths Chapter 6 ત્રિકોણ Ex 6.2 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 10 Maths Chapter 6 ત્રિકોણ Ex 6.2
પ્રશ્ન 1.
આકૃતિ (1) અને (2)માં, DE || BC.
(i) માં EC શોધો.
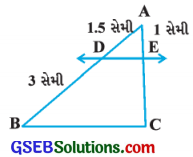
ઉત્તરઃ
બંને આકૃતિમાં રેખા DE એ ∆ABCની બાજુઓ AB અને ACને અનુક્રમે D અને Eમાં છેદે છે તથા DE || BC.
∴ \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)
∴ EC = \(\frac{1 \times 3}{1.5}\)
(ii) માં AD શોધો.
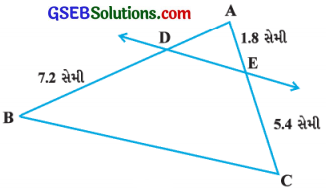
ઉત્તરઃ
\(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)
AD = \(\frac{1.8 \times 7.2}{5.4}\)
AD = 2.4 સેમી
પ્રશ્ન 2.
બિંદુઓ E અને F એ APQRની બાજુઓ અનુક્રમે PQ અને PR પર આવેલાં છે. નીચેના દરેક વિકલ્પમાં EF || QR છે કે કે કેમ તે જણાવો?
(i) PE = 3.9 સેમી, EQ = 3 સેમી, PF = 3.6 સેમી અને FR = 2.4 સેમી.
(ii) PE = 4 સેમી, E = 4.5 સેમી, PF = 8 સેમી અને RF = 9 સેમી.
(iii) PQ = 1.28 સેમી, PR = 2.56 સેમી, PE = 0.18 સેમી અને P = 0.36 સેમી.
ઉત્તરઃ
બિંદુઓ E અને F ∆ PQRની બાજુઓ અનુક્રમે PQ અને PR પર આવેલાં છે.
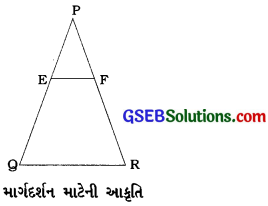
(i) અહીં, \(\frac{\mathrm{PE}}{\mathrm{EQ}}=\frac{3.9}{3}=\frac{1.3}{1}\) અને
\(\frac{\mathrm{PF}}{\mathrm{FR}}=\frac{3.6}{2.4}=\frac{1.5}{1}\)આથી \(\frac{\mathrm{PE}}{\mathrm{EQ}} \neq \frac{\mathrm{PF}}{\mathrm{FR}}\)
આથી પ્રમેય 6.2 મુજબ, EF || QR નથી.
(ii) અહીં, \(\frac{\mathrm{PE}}{\mathrm{QE}}=\frac{4}{4.5}=\frac{8}{9}\) અને
\(\frac{\mathrm{PF}}{\mathrm{RF}}=\frac{8}{9}\)આથી \(\frac{\mathrm{PE}}{\mathrm{QE}}=\frac{\mathrm{PF}}{\mathrm{RF}}\)
આથી પ્રમેય 6.2 મુજબ, ET || GR.
(iii) અહીં, \(\frac{\mathrm{PE}}{\mathrm{PQ}}=\frac{0.18}{1.28}=\frac{9}{64}\) અને
\(\frac{\mathrm{PF}}{\mathrm{PR}}=\frac{0.36}{2.56}=\frac{9}{64}\) તેથી
\(\frac{\mathrm{PE}}{\mathrm{PQ}}=\frac{\mathrm{PF}}{\mathrm{PR}}\)આથી પ્રમેય 6.2 મુજબ, EF || QR.
પ્રશ્ન 3.
આપેલ આકૃતિમાં, જો LM || CB અને LN || CD હોય, તો સાબિત કરો કે, \(\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AN}}{\mathrm{AD}}\)
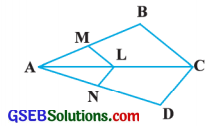
ઉત્તરઃ
∆ ABCમાં, LM || CB અને LM જો ABને Mમાં તથા ACને Lમાં છેદે છે.
∴ \(\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AL}}{\mathrm{AC}}\) (પ્રમેય 6.1 પરથી) ……… (1)
∆ ACDમાં, LN || CD અને CN એ ACને Lમાં તથા ADને Nમાં છેદે છે.
∴ \(\frac{\mathrm{AL}}{\mathrm{AC}}=\frac{\mathrm{AN}}{\mathrm{AD}}\) (પ્રમેય 6.1 પરથી) ……….. (2)
(1) અને (2) પરથી, \(\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AN}}{\mathrm{AD}}\)
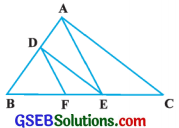
પ્રશ્ન 4.
આપેલ આકૃતિમાં, જો DE || AC અને DF || AE હોય, તો સાબિત કરો કે, \(\frac{B F}{F E}=\frac{B E}{E C}\) .
ઉત્તરઃ
∆ ABEમાં, DF || AE તથા DF એ AB અને BEને અનુક્રમે D અને Fમાં છેદે છે.
∴ \(\frac{\mathrm{BF}}{\mathrm{FE}}=\frac{\mathrm{BD}}{\mathrm{DA}}\) (પ્રમેય 6.1) …………. (1)
∆ ABCમાં, DE II AC તથા DE એ BA અને BCને અનુક્રમે D અને Eમાં છેદે છે.
∴ \(\frac{\mathrm{BD}}{\mathrm{DA}} \doteq \frac{\mathrm{BE}}{\mathrm{EC}}\) (પ્રમેય 6.1) ………….(2)
(1) અને (2) પરથી, \(\).
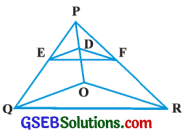
પ્રશ્ન 5.
આપેલ આકૃતિમાં, DE || OQ અને DF || QR. સાબિત કરો કે, EF || QR.
ઉત્તરઃ
∆ PQOમાં, DE || OQ
∴ \(\frac{\mathrm{PE}}{\mathrm{EQ}}=\frac{\mathrm{PD}}{\mathrm{DO}}\) (પ્રમેય 6.1) …………..(1)
∆ PORમાં, DF || OR
∴ \(\frac{\mathrm{PD}}{\mathrm{DO}}=\frac{\mathrm{PF}}{\mathrm{FR}}\) (પ્રમેય 6.1) ……………(2)
(1) અને (2) પરથી, = \(\frac{\mathrm{PE}}{\mathrm{EQ}}=\frac{\mathrm{PF}}{\mathrm{FR}}\)
હવે, રેખા SF એ ∆ PQRની બાજુઓ PG અને PRને અનુક્રમે E અને Fમાં છેદે છે તથા \(\frac{\mathrm{PE}}{\mathrm{EQ}}=\frac{\mathrm{PF}}{\mathrm{FR}}\)
આથી પ્રમેય 6.2 મુજબ, EF || GR.
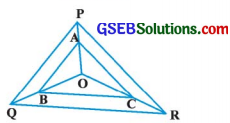
પ્રશ્ન 6.
આપેલ આકૃતિમાં, AB || PQ અને AC || PR બને તે રીતે બિંદુઓ A, B અને C અનુક્રમે OP, OQ અને OR પર આવેલાં છે, તો સાબિત કરો કે BC || QR.
ઉત્તરઃ
∆ OPQમાં, AB || PO અને AB એ OP અને 20ને અનુક્રમે A અને Bમાં છેદે છે.
∴ \(\frac{\mathrm{OA}}{\mathrm{AP}}=\frac{\mathrm{OB}}{\mathrm{BQ}}\) (પ્રમેય 6.1) ……………. (1)
∆ OPRમાં, AC || PR અને AC એ OP અને ORને અનુક્રમે A અને Cમાં છેદે છે.
\(\frac{\mathrm{OA}}{\mathrm{AP}}=\frac{\mathrm{OC}}{\mathrm{CR}}\) (પ્રમેય 6.1) ……….. (2)
(1) અને (2) પરથી, \(\frac{\mathrm{OB}}{\mathrm{BQ}}=\frac{\mathrm{OC}}{\mathrm{CR}}\) ‘
∆ OQRમાં, BC એ OQ અને ORને અનુક્રમે B અને Cમાં છેદે છે અને \(\frac{\mathrm{OB}}{\mathrm{BQ}}=\frac{\mathrm{OC}}{\mathrm{CR}}\)
∴ BC || OR (પ્રમેય 6.2)
પ્રશ્ન 7.
પ્રમેય 6.1નો ઉપયોગ કરીને, સાબિત કરો કે ત્રિકોણની એક છે બાજુના મધ્યબિંદુમાંથી પસાર થતી અને બીજી બાજુને સમાંતર રેખા, ત્રીજી બાજુને દુભાગે છે. (યાદ કરો, તમે ધોરણ 1માં આ પરિણામ સાબિત કર્યું છે.)
ઉત્તરઃ
પક્ષ: ∆ ABCમાં, P એ બાજુ ABનું મધ્યબિંદુ છે. Pમાંથી દોરેલ BC ને સમાંતર રેખા AC ને 9માં છેદે છે.
સાધ્ય: Q એ AC નું મધ્યબિંદુ છે.
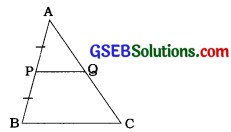
સાબિતીઃ ∆ ABCમાં, P અને Q અનુક્રમે AB અને AC પર આવેલ બિંદુઓ છે તથા PQ || BC.
\(\frac{\mathrm{AP}}{\mathrm{PB}}=\frac{\mathrm{AQ}}{\mathrm{QC}}\) (પ્રમેય 6.1) …… (1)
હવે, P એ ABનું મધ્યબિંદુ છે.
∴ AP = PB
∴ \(\frac{\mathrm{AP}}{\mathrm{PB}}\) = 1 ………..(2)
(1) અને (2) પરથી,
\(\frac{\mathrm{AQ}}{\mathrm{QC}}\) = 1
AQ = QC
Q એ ACનું મધ્યબિંદુ છે.
નોંધઃ ધોરણ IXમાં આ જ પરિણામ સમાંતરબાજુ ચતુષ્કોણના ૪ nગુણધર્મોની મદદથી સાબિત કરેલ હતું.
પ્રશ્ન 8.
પ્રમેય 6.2નો ઉપયોગ કરીને, સાબિત કરો કે ત્રિકોણની બે બાજુઓનાં મધ્યબિંદુઓમાંથી પસાર થતી રેખા ત્રિકોણની ત્રીજી બાજુને સમાંતર હોય છે. (યાદ કરો, તમે ધોરણ IXમાં આ પરિણામ સાબિત કર્યું છે.)
ઉત્તરઃ
પક્ષ: ∆ABCમાં, P અને 9 અનુક્રમે AB અને ACના મધ્યબિંદુ છે.
સાધ્ય: PQ || BC
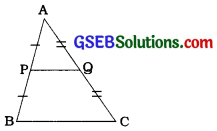
સાબિતીઃ અહીં, P એ ABનું મધ્યબિંદુ છે.
∴ AP = PB
∴ \(\frac{\mathrm{AP}}{\mathrm{PB}}\) = 1 ………….(1)
અહીં, Q એ ACનું મધ્યબિંદુ છે.
∴ AQ = QC
∴ \(\frac{\mathrm{AQ}}{\mathrm{QC}}\) = 1 …………. (2)
આમ, (1) અને (2) પરથી,
હવે, ∆ ABCમાં P અને Q બિંદુઓ અનુક્રમે AB અને AC પર આવેલાં છે અને \(\frac{\mathrm{AP}}{\mathrm{PB}}=\frac{\mathrm{AQ}}{\mathrm{QC}}\)
∴ પ્રમેય 6.2 મુજબ, PQ || BC.
પ્રશ્ન 9.
સમલંબ ચતુષ્કોણ ABCDમાં AB || DC અને તેના વિકર્ણો એકબીજાને બિંદુ 0માં છેદે છે, સાબિત કરો કે \(\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}\).
ઉત્તરઃ
પક્ષ: સમલંબ ચતુષ્કોણ ABCDમાં AB || DC અને વિકર્ણી AC અને BD એકબીજાને બિંદુ 0માં છેદે છે.
સાધ્ય: \(\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}\)
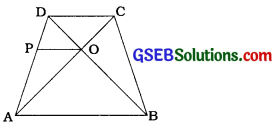
રચનાઃ 0માંથી પસાર થતી ABને સમાંતર રેખા દોરો, જે ADને Pમાં છે.
સાબિતી: અહીં, OP || AB અને AB || DC
∴ OP || DC
∆ ADCમાં, OP || DC અને બિંદુઓ P તથા O અનુક્રમે AD અને AC પર આવેલાં છે.
\(\frac{\mathrm{OA}}{\mathrm{OC}}=\frac{\mathrm{PA}}{\mathrm{PD}}\) (પ્રમેય 6.1) ……………. (1)
∆ DABમાં, OPI AB અને બિંદુઓ P તથા 0 અનુક્રમે AD અને BD પર આવેલાં છે.
∴ \(\frac{\mathrm{PA}}{\mathrm{PD}}=\frac{\mathrm{OB}}{\mathrm{OD}}\) (પ્રમેય 6.1) ………………(2)
(1) અને (2) પરથી,
\(\frac{\mathrm{OA}}{\mathrm{OC}}=\frac{\mathrm{OB}}{\mathrm{OD}}\)∴ \(\frac{\mathrm{OA}}{\mathrm{OB}}=\frac{\mathrm{OC}}{\mathrm{OD}}\)
∴ \(\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}\)
પ્રશ્ન 10.
ચતુષ્કોણ ABCDના વિકર્ણો એકબીજાને બિંદુ 0માં છેદે છે અને તેથી \(\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}\) થાય છે, તો સાબિત કરો કે ABCD સમલંબ ચતુષ્કોણ છે.
ઉત્તરઃ
પક્ષ: ચતુષ્કોણ ABCDના વિકણ એકબીજાને બિંદુ 0માં છેદે છે અને \(\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}\)
સાધ્ય: ABCD સમલંબ ચતુષ્કોણ છે.
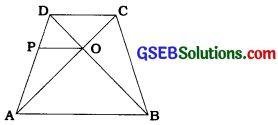
રચનાઃ બિંદુ 0માંથી ABને સમાંતર રેખા દોરો, જે ADને બિંદુ Pમાં છે.
સાબિતી: અહીં, ∆ DABમાં, બિંદુઓ P અને A અનુક્રમે DA અને DB પર આવેલાં છે અને PO || AB.
∴ \(\frac{\mathrm{AP}}{\mathrm{DP}}=\frac{\mathrm{BO}}{\mathrm{DO}}\) (પ્રમેય 6.1) ………….(1)
હવે, \(\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}\)
∴ \(\frac{\mathrm{AO}}{\mathrm{CO}}=\frac{\mathrm{BO}}{\mathrm{DO}}\) ………… (2)
(1) અને (2) પરથી,
\(\frac{\mathrm{AP}}{\mathrm{DP}}=\frac{\mathrm{AO}}{\mathrm{CO}}\)
હવે, ∆ ADCમાં, બિંદુઓ P અને A અનુક્રમે AD અને AC પર આવેલાં છે અને \(\frac{\mathrm{AP}}{\mathrm{DP}}=\frac{\mathrm{AO}}{\mathrm{CO}}\)
પ્રમેય 6.2 મુજબ, PO || DC.
હવે, રચના મુજબ PO || AB અને ઉપર સાબિત ક્ય મુજબ PO || DC.
∴ AB || DC આમ, ચતુષ્કોણ ABCDમાં, AB || DC.
આથી ABCD સમલંબ ચતુષ્કોણ છે.