Gujarat Board GSEB Solutions Class 6 Maths Chapter 3 સંખ્યા સાથે Ex 3.5 Textbook Exercise Questions and Answers.
Gujarat Board Textbook Solutions Class 6 Maths Chapter 3 સંખ્યા સાથે Ex 3.5
પ્રશ્ન 1.
નીચેનામાંથી કયું વિધાન સાચું છે?
(a) જો કોઈ સંખ્યા 3થી વિભાજ્ય છે, તો તે 9થી વિભાજ્ય હોય છે.
જવાબ:
ખોટું કારણ 9નો અવયવ 3 છે પણ 3નો અવયવ 9 નથી. આથી સંખ્યા 3 વડે વિભાજ્ય હોય, તે 9 વડે વિભાજ્ય ન પણ હોય.
(b) જો એક સંખ્યા 9થી વિભાજ્ય છે, તો તે ૩થી ચોક્કસ વિભાજ્ય હશે.
જવાબઃ
સાચું કારણઃ 9નો અવયવ 3 છે તેથી જો સંખ્યા 9થી વિભાજ્ય હોય, તો તે 3થી ચોક્કસ વિભાજ્ય હોય.
(c) એક સંખ્યા 18થી વિભાજ્ય છે, તો તે 3 અને 6 બંનેથી વિભાજ્ય હોય.
જવાબઃ
સાચું કારણ 3 અને 6 બંને 18ના અવયવો છે.
(d) જો એક સંખ્યા 9 અને 10 બંનેથી વિભાજ્ય હોય, તો તે 90થી વિભાજ્ય હોઈ શકે.
જવાબઃ
સાચું કારણ 9 અને 10 બંને સહ-અવિભાજ્ય સંખ્યાઓ છે. હવે જો સંખ્યાને બે સહ-અવિભાજ્ય સંખ્યાઓ વડે ભાગી શકાય તો આ સંખ્યાને આ બે સહ-અવિભાજ્ય સંખ્યાઓના ગુણાકાર વડે પણ ભાગી શકાય.
(e) જો બે સંખ્યા સહ-અવિભાજ્ય હોય, તો એમાંથી ઓછામાં ઓછી એક સંખ્યા ચોક્કસ અવિભાજ્ય સંખ્યા હશે.
જવાબઃ
ખોટું કારણઃ બે સંખ્યાઓનો સામાન્ય અવયવ 1 હોય, તો તે બે સંખ્યાઓ સહ અવિભાજ્ય સંખ્યાઓ કહેવાય. તેથી એ જરૂરી નથી કે બેમાંથી એક સંખ્યા અવિભાજ્ય સંખ્યા જ હોય. જુઓ 4 અને 9 એ સહ-અવિભાજ્ય સંખ્યાઓ છે છતાં તેમાંની એકેય સંખ્યા અવિભાજ્ય નથી.
(f) 4થી વિભાજ્ય બધી જ સંખ્યાઓ 8થી પણ ચોક્કસ વિભાજ્ય હોવી જોઈએ.
જવાબઃ
ખોટું કારણ 8નો અવયવ 4 છે. તેથી આ સાચું નથી. જુઓ 28ને 4 વડે ભાગી શકાય છે પણ 8 વડે ભાગી શકાતા નથી.
(g) 8થી વિભાજ્ય બધી જ સંખ્યાઓ 4થી વિભાજ્ય હોવી જોઈએ.
જવાબ:
સાચું
કારણ: 8નો અવયવ 4 છે. તેથી જે સંખ્યા 8 વડે વિભાજ્ય હોય તે સંખ્યા 4 વડે પણ વિભાજ્ય હોય જ. જુઓ 24 ÷ 8 = 3 અને 24 ÷ 4 = 6
(h) જો કોઈ સંખ્યા બે સંખ્યાઓને અલગ અલગ સંપૂર્ણપણે વિભાજિત કરે છે, તો તે સંખ્યા તેના સરવાળાને પણ સંપૂર્ણપણે વિભાજિત કરશે.
જવાબઃ
સાચું
કારણઃ જુઓ 7 વડે 21ને અને 7 વડે 35ને ભાગી શકાય છે. તેથી 7 વડે આ બે સંખ્યાઓના સરવાળા 21 + 35 = 56ને ભાગી શકાય છે.
(i) જો કોઈ સંખ્યા બે સંખ્યાઓના સરવાળાને પૂર્ણ રીતે વિભાજિત કરે છે, તો તે બંને સંખ્યાઓને અલગ અલગ રીતે પણ વિભાજિત કરશે.
જવાબ:
ખોટું
કારણ: જુઓ 10 અને 4ના સરવાળા 14ને 7 વડે ભાગી શકાય છે. પણ 10ને કે 4ને 7 વડે ભાગી શકાતા નથી.
![]()
પ્રશ્ન 2.
અહીં 60 માટે બે જુદા જુદા અવયવ-વૃક્ષો આપ્યાં છે. ખૂટતી સંખ્યાઓ લખો:
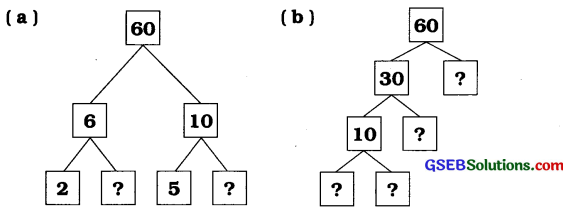
જવાબ:
(a) ∵ 6 = 2 × 3 અને 10 = 5 × 2
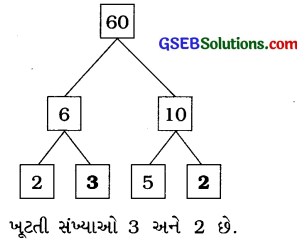
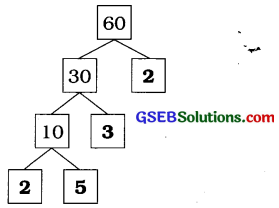
(b) ∵ 60 = 30 × 2
30 = 10 × 3
અને 10 = 2 × 5
∴ ખૂટતી સંખ્યાઓ 2, 3, 2 અને 5 છે.
પ્રશ્ન 3.
સંખ્યા સાથે રમત ૩. વિભાજ્ય સંખ્યાના અવિભાજ્ય અવયવો પાડવામાં કયા અવયવોનો સમાવેશ થતો નથી?
જવાબ:
અવયવ 1 અને સંખ્યા 1 પોતે આ બંનેનો સમાવેશ વિભાજ્ય સંખ્યાના અવિભાજ્ય અવયવોમાં કરવામાં આવતો નથી.
પ્રશ્ન 4.
4 અંકની સૌથી મોટી સંખ્યા લખો અને તેને અવિભાજ્ય અવયવની રીતે રજૂ કરો.
જવાબ:
ચાર અંકની સૌથી મોટી સંખ્યા 9999 છે.

પ્રશ્ન 5.
5 અંકની નાનામાં નાની સંખ્યા લખો અને તેને અવિભાજ્ય અવયવની રીતે રજૂ કરો.
જવાબ:
પાંચ અંકની નાનામાં નાની સંખ્યા 10000 છે.

∴ 10000ના અવિભાજ્ય અવયવો = 2 × 2 = 2 × 2 × 5 × 5 × 5 × 5 2500 આમ, 10000 = 2 × 2 × 2 × 2 × 5 × 5 × 5 × 5
પ્રશ્ન 6.
1729ના બધા અવિભાજ્ય અવયવ જણાવો અને તેને ઊતરતા ક્રમમાં ગોઠવો. હવે તે બે ક્રમિક આવેલા અવિભાજ્ય અવયવોમાં જો કોઈ સંબંધ હોય તો લખો.
જવાબ:
1729ના અવિભાજ્ય અવયવો = 7 × 13 × 19
1729 1729ના અવિભાજ્ય અવયવો ઊતરતા
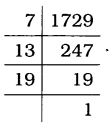
ક્રમમાં : 19, 13 અને 7
હવે, 19 – 13 = 6 તથા 13 – 7 = 6
એ સ્પષ્ટ છે કે અહીં ક્રમિક બે અવિભાજ્ય અવયવોનો તફાવત 6 છે.
![]()
પ્રશ્ન 7.
ત્રણ ક્રમિક સંખ્યાઓનો અવયવી હંમેશાં 6થી વિભાજ્ય હોય છે. આ વિધાનને કેટલાંક ઉદાહરણની મદદથી સ્પષ્ટ કરો.
જવાબ:
(i) આપણે ક્રમિક ત્રણ સંખ્યાઓ 8, 9 અને 10 લઈએ.
આ ત્રણ સંખ્યાઓનો ગુણાકાર = 8 × 9 × 10 = 720
720નો પ્રથમ અવયવી 720 છે.
જુઓઃ 720 ÷ 6 = 120
(ii) આપણે ક્રમિક ત્રણ સંખ્યાઓ 11, 12 અને 13 લઈએ.
આ ત્રણ સંખ્યાઓનો ગુણાકાર = 11 × 12 × 11 = 1716
1716નો પ્રથમ અવયવી 1716 છે.
જુઓઃ
1716 ÷ 6 = 286
પ્રશ્ન 8.
કોઈ પણ બે ક્રમિક વિષમ (એકી) સંખ્યાઓનો સરવાળો 4થી વિભાજ્ય છે. કેટલાંક ઉદાહરણની મદદથી આ વિધાન સ્પષ્ટ કરો.
(i) આપણે ક્રમિક બે વિષમ (એકી) સંખ્યાઓ 11 અને 18 લઈએ.
જુઓઃ
11 + 18 = 24 અને 24 – 4 = 6
(ii) આપણે ક્રમિક બે વિષમ (એકી) સંખ્યાઓ 29 અને 31 લઈએ.
જુઓઃ
29 + 31 = 60 અને 60 + 4 = 15
આમ, ક્રમિક બે વિષમ (એક) સંખ્યાઓના સરવાળાને હંમેશાં 4 વડે ભાગી શકાય છે.
પ્રશ્ન 9.
નીચેનામાંથી કઈ સંખ્યાઓમાં અવિભાજ્ય અવયવો ક્યા છે?
(a) 24 = 2 × 3 × 4
(b) 56 = 72 × 2 × 2
(c) 70 = 2 × 5 × 7
(d) 54 = 2 × 3 × 9
જવાબ:
(a) 24 = 2 × 3 × 4
અહીં 4 એ અવિભાજ્ય અવયવ નથી. (∵ 4 = 2 × 2)
∴ અવિભાજ્ય અવયવીકરણ થયું નથી.
(b) 56 = 7 × 2 2 × 2
અહીં 7 અને 2 બંને અવિભાજ્ય અવયવો છે.
∴ અવિભાજ્ય અવયવીકરણ થયું છે.
(c) 70 = 2 × 5 × 7
અહીં 2, 5 અને 7 ત્રણે અવિભાજ્ય અવયવો છે.
∴ અવિભાજ્ય અવયવીકરણ થયું છે.
(d) 54 = 2 × 3 × 9
અહીં 9 એ અવિભાજ્ય અવયવ નથી. (∵ 9 = 3 × 3)
∴ અવિભાજ્ય અવયવીકરણ થયું નથી.
પ્રશ્ન 10.
25110 એ 45થી વિભાજ્ય છે કે નહીં તે નક્કી કરો.
(નોંધઃ 5 અને 9 સહ-અવિભાજ્ય સંખ્યાઓ છે. આપેલી સંખ્યાને 5 અને 9ની વિભાજ્યતાની ચાવીથી ચકાસો.)
જવાબ:
જો સંખ્યા બે ક્રમિક સહ-અવિભાજ્ય સંખ્યાઓથી વિભાજ્ય હોય, તો સંખ્યા તેમના ગુણાકારથી પણ વિભાજ્ય હોય. જુઓ 45 = 5 × 9 જ્યાં 5 અને 9 એ સહ-અવિભાજ્ય સંખ્યાઓ છે. સંખ્યા 25110નો એકમનો અંક 1 છે તેથી 25110 એ 5 વડે વિભાજ્ય છે. સંખ્યા 25110ના અંકોનો સરવાળો = 0 + 1 + 1 + 5 + 2 = 9
∴ 25110 એ 3 વડે વિભાજ્ય છે.
આમ, 25110 એ 5 વડે અને 3 વડે વિભાજ્ય છે જ્યાં 5 અને 9 એ સહ-અવિભાજ્ય સંખ્યાઓ છે.
∴ હા, 25110 એ 45 વડે વિભાજ્ય છે.
પ્રશ્ન 11.
સંખ્યા 18, 2 અને 3 બંને સંખ્યાથી વિભાજ્ય છે. તે 2 × ૩ = 6થી પણ વિભાજ્ય છે. એ જ પ્રમાણે એક સંખ્યા 4 અને 6 બંને સંખ્યાથી વિભાજ્ય છે. શું આપણે કહી શકીએ કે તે સંખ્યા 4 × 6 = 24થી પણ વિભાજ્ય હશે. જો નહિ હોય, તો તમારા જવાબને ચકાસવા માટે એક ઉદાહરણ આપો.
જવાબ:
આપેલી સંખ્યા બે સહ-અવિભાજ્ય સંખ્યાઓ વડે વિભાજ્ય હોય, તો તેમના ગુણાકાર વડે સંખ્યા વિભાજ્ય હોય.
અહીં 2 અને 3 એ સહ-અવિભાજ્ય સંખ્યાઓ છે.
∴ 18 એ તેમના ગુણાકાર 2 × 3 વડે એટલે કે 6 વડે વિભાજ્ય છે.
હવે, 4 અને 6 એ સહ-અવિભાજ્ય સંખ્યાઓ નથી.
∴ સંખ્યાને 4 અને 6ના ગુણાકાર 4 × 6 વડે એટલે કે 24 વડે વિભાજ્ય નથી. બીજી એક સંખ્યા 36 લઈએ. 36 એ 4 અને 6 બંને વડે વિભાજ્ય છે. પરંતુ 36 એ 4 અને 6ના ગુણાકાર 24 વડે વિભાજ્ય નથી.
પ્રશ્ન 12.
હું ચાર જુદા જુદા અવિભાજ્ય અવયવવાળી સૌથી નાની સંખ્યા છું. શું તમે મને ઓળખી શકો છો?
જવાબ:
અહીં સૌથી નાનામાં નાની સંખ્યા શોધવાની છે. સૌથી નાનામાં નાની ભિન્ન ચાર અવિભાજ્ય સંખ્યાઓ 2, 3, 5 અને 7 છે.
∴ ચાર ભિન્ન નાનામાં નાની અવિભાજ્ય સંખ્યાઓવાળી સંખ્યા = 2 × 3 × 5 × 7 = 210
આમ, આ સંખ્યા 210 છે.