Gujarat Board GSEB Solutions Class 10 Maths Chapter 11 રચના Ex 11.1 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 10 Maths Chapter 11 રચના Ex 11.1
નીચેના પૈકી પ્રત્યેકની રચના કરી, તેની રચનાના મુદ્દા તથા તેની યથાર્થતા આપોઃ
પ્રશ્ન 1.
7.6 સેમી લંબાઈનો રેખાખંડ દોરી, તેનું 5 : 8 ગુણોત્તરમાં વિભાજન કરો. બંને ભાગ માપો.
ઉત્તર:
પક્ષ: 7.6 સેમી લંબાઈનો રેખાખંડ AB આપેલ છે.
કૃત્ય: ABનું 58 ગુણોત્તરમાં વિભાજન કરતું બિંદુ C મેળવવું તથા AC અને BC માપવા.
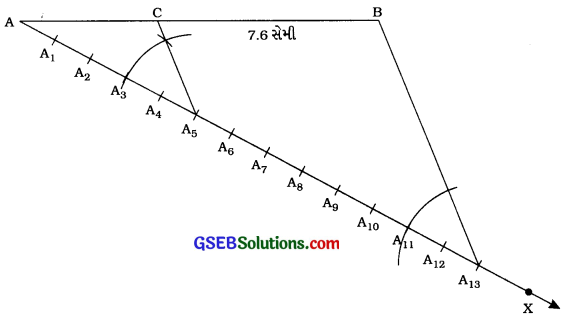
રચનાના મુદ્દા:
(1) AB સાથે લઘુકોણ બનાવે તેવું કોઈ પણ કિરણ AX રચો.
(2) AX પર AA1 = A1A2 = A2A3 = …………… = A12A13 થાય તેવાં 13 (5 + 8) બિંદુઓ A1, A2, A3, ………., A13 નાં સ્થાન નક્કી કરો.
(3) BA13 જોડો.
(4) બિંદુ A5 માંથી ABને સમાંતર હોય તેવી રેખા દોરો, જે ABને C બિંદુમાં છે. આ માટે ∠AA13Bને સમાન હોય તેવો ∠AA5C રચો.
(5) આ રીતે મળતું બિંદુ C એ ABનું 5: 8 ગુણોત્તરમાં વિભાજન કરતું બિંદુ છે. એટલે કે, AC : CB = 5 : 8.
ABના બે ભાગ માપતા આપણને AC = 2.9 સેમી અને BC = 4.7 સેમી મળે.

યથાર્થતા :
રચના મુજબ, A5C || A13B.
આથી ∆ AA13Bમાં \(\frac{\mathrm{AC}}{\mathrm{CB}}=\frac{\mathrm{AA}_{5}}{\mathrm{~A}_{5} \mathrm{~A}_{13}}\) મળે. (BPT)
પરંતુ રચના મુજબ, \(\frac{\mathrm{AA}_{5}}{\mathrm{~A}_{5} \mathrm{~A}_{13}}=\frac{5}{8}\)
\(\frac{\mathrm{AC}}{\mathrm{BC}}=\frac{5}{8}\)
આમ, બિંદુ C એ AB નું 5: 8 ગુણોત્તરમાં વિભાજન કરતું બિંદુ છે.
વૈકલ્પિક રીતઃ
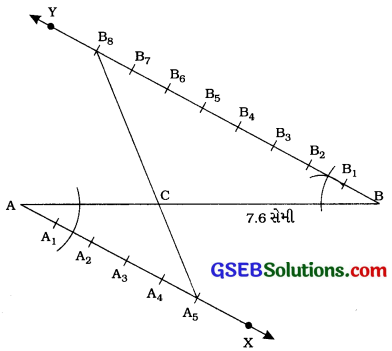
રચનાના મુદ્દા :
(1) AB ની સામસામેની (વિરુદ્ધ) બાજુઓમાં કિરણ AX અને BY એવાં દોરો કે, જેથી ∠BAX અને ∠ABY સમાન ખૂણા થાય.
(સરળતા ખાતર ∠BAX = ∠ABY = 60° થાય તેવાં કિરણ AX અને BH દોરો.)
(2) AX પર પાંચ બિંદુઓ A1, A2, A3, A4 તથા A5 અને BY પર આઠ બિંદુઓ B1, B2, B3, B4, B5, B6, B7, B8 નાં સ્થાન એવાં નક્કી કરો, જેથી AA1 = A1A2 = A2A3 = A3A4 = A4A5 = BB1 = B1B2 = B2B3 = B3B4 = B4B5 = B5B6 = B6B7 = B7B8 થાય.
(3) B8A5 દોરો જે ABને C બિંદુમાં છેદે.
(4) આ રીતે મળતું બિંદુ C એ AB નું 5 : 8 ગુણોત્તરમાં વિભાજન કરતું બિંદુ છે. એટલે કે, AC : CB = 5 : 8.
યથાર્થતા:
∆ CAA5; અને ∆ CBB8માં, ∠CAA = ∠CBB8 (રચના મુજબ) અને ∠ACA5 = ∠BCB8.
∴ ખૂબૂ શરત મુજબ, ∆ CAA5 – ∆ CBB8
∴ \(\frac{\mathrm{CA}}{\mathrm{CB}}=\frac{\mathrm{AA}_{5}}{\mathrm{BB}_{8}}\)
પરંતુ રચના મુજબ, \(\frac{\mathrm{AA}_{5}}{\mathrm{BB}_{8}}=\frac{5}{8}\)
∴ \(\frac{\mathrm{CA}}{\mathrm{CB}}=\frac{5}{8}\)
∴ AC : CB = 5 : 8
આમ, બિંદુ C એ ABનું 5: 8 ગુણોત્તરમાં વિભાજન કરતું બિંદુ છે.

પ્રશ્ન 2.
4 સેમી, 5 સેમી અને 6 સેમી બાજુવાળા ત્રિકોણની રચના કરો અને પછી આ ત્રિકોણની બાજુઓને અનુરૂપ તે બાજુઓથી \(\frac{2}{3}\) ગણી બાજુવાળા ત્રિકોણની રચના કરો.
ઉત્તર:
કૃત્ય:
AB = 4 સેમી, BC = 6 સેમી અને AC = 5 સેમી હોય તેવો ∆ ABC રચવો અને ત્યારબાદ ∆ ABC ને સમરૂપ હોય તેવો એક ત્રિકોણ રચવો, જેની અનુરૂપ બાજુઓનો ત્રિકોણ ABC ની બાજુઓ સાથેનો ગુણોત્તર \(\frac{2}{3}\) હોય
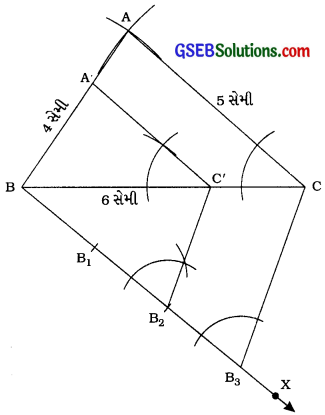
રચનાના મુદ્દા :
(1) ∆ ABC રચો, જેમાં AB = 4 સેમી, BC = 6 સેમી અને AC = 5 સેમી હોય.
(2) BC ના જે અર્ધતલમાં બિંદુ A હોય તેનાથી વિરુદ્ધ અર્ધતલમાં કિરણ” BX દોરો, જેથી ∠CBX લઘુકોણ થાય.
(3) BB1 = B1B2 = B2B3 થાય તેવાં ત્રણ બિંદુઓ B1, B2 અને B3 ને BX પર અંકિત કરો.
(4) BC જોડો.
(5) B2 માંથી B3Cને સમાંતર રેખા દોરો, જે BCને C’માં છે. આ માટે ∠BB3C ને સમાન હોય તેવો ∠BB2C રચો.
(6) ∠BCAને સમાન ∠BC’A’ રચો જેથી કિરણ C’A’ એ BAને A’માં છે અને C’A’ || CA થાય.
આથી ∆ A’BC’ એ માગેલ માપ મુજબનો ∆ ABCને સમરૂપ હોય તેવો ત્રિકોણ છે અને ∆ A’BC’ની બાજુઓ તથા ∆ ABCની અનુરૂપ બાજુઓનો ગુણોત્તર છે.
યથાર્થતાઃ
∆ BB3Cમાં, B2C’ || B3C .
∆ BB2C’ ~ ∆ BB3C (ખૂખૂબૂ શરત મુજબ)
\(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{BB}_{2}}{\mathrm{BB}_{3}}=\frac{2}{3}\) ……………. (1)
∆ BACમાં, A’C’ || AC
∆ BAC ~ ∆ BA’C’
\(\frac{\mathrm{BA}^{\prime}}{\mathrm{BA}}=\frac{\mathrm{A}^{\prime} \mathrm{C}^{\prime}}{\mathrm{AC}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}\) …………. (2)
(1) અને (2) પરથી,
\(\frac{B A^{\prime}}{B A}=\frac{A^{\prime} C^{\prime}}{A C}=\frac{B C^{\prime}}{B C}=\frac{2}{3}\).

પ્રશ્ન 3.
5 સેમી, 6 સેમી અને 7 સેમી બાજુવાળા ત્રિકોણની રચના કરો અને પછી બીજો ત્રિકોણ રચો, જેની બાજુઓ પ્રથમ ત્રિકોણની અનુરૂપ બાજુઓ કરતાં \(\frac{7}{5}\) ગણી હોય.
ઉત્તર:
કૃત્ય : AB = 5 સેમી, BC = 7 સેમી અને AC = 6 સેમી હોય તેવો ∆ ABC રચવો અને ત્યારબાદ ∆ ABC ને સમરૂપ હોય તેવો એક ત્રિકોણ રચવો, જેની અનુરૂપ બાજુઓનો AABCની બાજુઓ સાથેનો ગુણોત્તર \(\frac{7}{5}\) હોય.
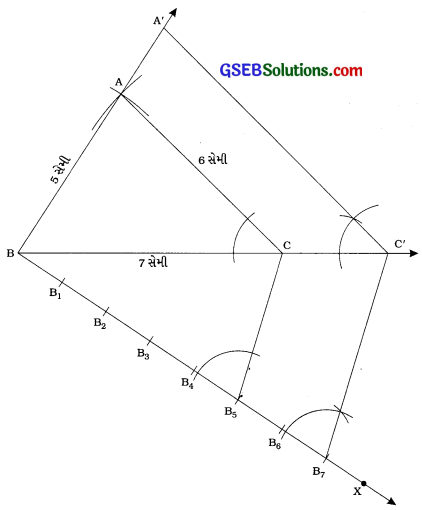
રચનાના મુદ્દા:
(1) ∆ ABC રચો, જેમાં AB = 5 સેમી, BC = 7 સેમી અને AC = 6 સેમી હોય.
(2) BCના જે અર્ધતલમાં બિંદુ A હોય તેનાથી વિરુદ્ધ અર્ધતલમાં કિરણ BX દોરો, જેથી 2 CBX લઘુકોણ થાય.
(3) BB1 = B1B2 = B2B3 = … = B6B7 થાય તેવાં સાત બિંદુઓ B1, B2, B3, ……….., B7 ને BX પર અંકિત કરો.
(4) B5C જોડો.
(5) ∠BB7C’ = ∠BB5C રચીને B7માંથી પસાર થતી અને B5Cને સમાંતર રેખા દોરો, જે લંબાવેલ BCને C’માં છેદે.
(6) ∠BC’A’ = ∠BCA રચીને C’માંથી પસાર થતી અને CAને સમાંતર રેખા દોરો, જે લંબાવેલ BA ને A’માં છેદે.
આથી ∆ ABC’ એ માગેલ માપ મુજબનો ∆ A’B’C’ ને સમરૂપ હોય તેવો ત્રિકોણ છે અને ∆ ABC’ની બાજુઓ તથા ∆ ABC ની અનુરૂપ બાજુઓનો ગુણોત્તર : છે.
યથાર્થતાઃ
∆ BB7C’માં, B5C || B7C’
∴ ∆ BB7C’ ~ ∆ BB5C
∴ \(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{BB}_{7}}{\mathrm{BB}_{5}}=\frac{7}{5}\) ………..(1)
∴ ∆ ABC’માં AC || A’C’
∴ ∆ ABC’ = ∆ ABC
∴ \(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{A}^{\prime} \mathrm{C}^{\prime}}{\mathrm{AC}}\) ………….(2)
(1) અને (2) પરથી,
∴ \(\frac{\mathrm{AB}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{A}^{\prime} \mathrm{C}^{\prime}}{\mathrm{AC}}=\frac{7}{5}\).

પ્રશ્ન 4.
8 સેમી આધાર અને 4 સેમી વેધવાળા સમઢિબાજુ ત્રિકોણની રચના કરો અને પછી બીજો એવો ત્રિકોણ રચો, જેની બાજુઓ સમદ્વિભુજ ત્રિકોણની અનુરૂપ બાજુઓ કરતાં 1\(\frac{1}{2}\) ગણી હોય.
ઉત્તર:
કૃત્યઃ સમદ્વિબાજુ ∆ ABC રચવો, જેમાં આધાર BC = 8 સેમી અને વેધ AD = 4 સેમી હોય. ત્યારબાદ ∆ ABCને સમરૂપ હોય તેવો બીજો ત્રિકોણ રચવો, જેની બાજુઓ ∆ ABCની અનુરૂપ બાજુઓ કરતાં 1\(\frac{1}{2}\) ગણી હોય.
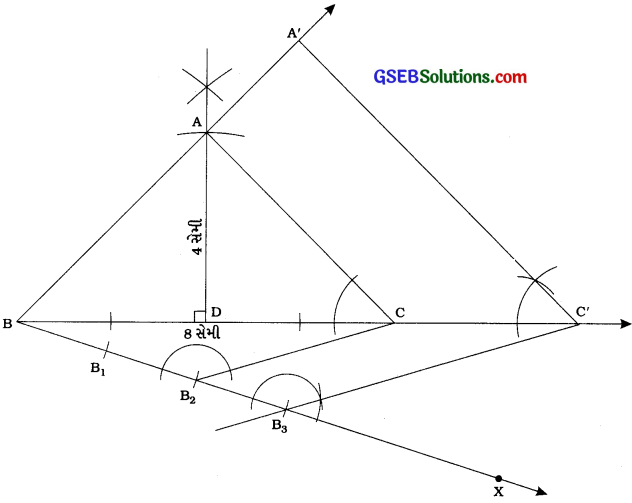
રચનાના મુદ્દા :
(1) સમદ્વિબાજુ ∆ ABC રચો, જેમાં પાયો BC = 8 સેમી અને વેધ AD = 4સેમી હોય.
(2) BCના જે અર્ધતલમાં બિંદુ A છે તેનાથી વિરુદ્ધ અર્ધતલમાં કિરણ BX દોરો, જેથી ∠CBX લઘુકોણ થાય.
(3) BB1 = B1B2 = B2B3 થાય તેવાં ત્રણ બિંદુઓ B1, B2 અને B3 ને BX પર અંકિત કરો.
(4) B2C જોડો.
(5) ∠BB3C’ = ∠BB2C રચીને B9માંથી પસાર થતી અને B2Cને સમાંતર રેખા દોરો, જે લંબાવેલ BCને c’માં છે.
(6) ∠BC’A’ = ∠BCA રચીને C માંથી પસાર થતી અને CAને સમાંતર રેખા દોરો, જે લંબાવેલ BAને ‘માં છે.
આથી ∆ A’B’C’ એ માગેલ માપ મુજબનો ∆ ABCને સમરૂપ હોય તેવો ત્રિકોણ છે અને ∆ ABCની બાજુઓ ∆ ABCની અનુરૂપ બાજુઓ કરતાં 1\(\frac{1}{2}\) ગણી છે.
યથાર્થતાઃ
∆ BB3C’માં, B2C || B3C’ .
∆ BB3C’ ~ ∆ BB2C
\(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{BB}_{3}}{\mathrm{BB}_{2}}=\frac{3}{2}\) …………. (1)
∆ ABCમાં, AC || A’C’
∆ A’BC’ = ∆ ABC
\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{A}^{\prime} \mathrm{C}^{\prime}}{\mathrm{AC}}\) ………….. (2)
(1) અને (2) પરથી,
\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{A}^{\prime} \mathrm{C}^{\prime}}{\mathrm{AC}}=\frac{3}{2}=1 \frac{1}{2}\)

પ્રશ્ન 5.
BC = 6 સેમી, AB = 3 સેમી અને ∠ABC = 60° હોય તેવો ત્રિકોણ ABC દોરો. પછી ∆ ABCની અનુરૂપ બાજુઓને તે પ્રમાણમાં હોય તેવી બાજુવાળા ત્રિકોણની રચના કરો.
ઉત્તર:
કૃત્ય BC = 6 સેમી, AB = 5 સેમી અને ∠ABC = 60° હોય તેવો ∆ ABC દોરવો. ત્યારબાદ ∆ ABCને સમરૂપ હોય તેવો એક ત્રિકોણ રચવો જેની બાજુઓનો A ABCની અનુરૂપ બાજુઓ સાથેનો ગુણોત્તર \(\frac{3}{4}\) હોય.
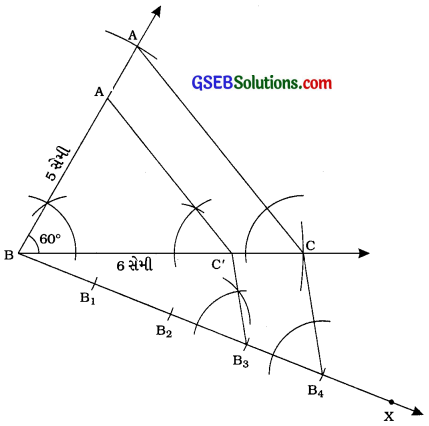
રચનાના મુદ્દા :
(1) BC = 6 સેમી, AB = 5 સેમી અને ∠ABC = 60° હોય તેવો A ABC રચો.
(2) BCના જે અર્ધતલમાં બિંદુ A છે તેનાથી વિરુદ્ધ અર્ધતલમાં કિરણ BX દોરો, જેથી ∠CBX લઘુકોણ થાય.
(3) BB1 = B1B2 = B2B3 = B3B4 થાય તેવાં ચાર બિંદુઓ B1, B2, B3 અને B4 ને BX પર અંકિત કરો.
(4) B4C જોડો.
(5) ∠BB3C’ = ∠BB4C રચીને Bકુમાંથી પસાર થતી અને B4Cને સમાંતર રેખા દોરો, જે BCને તેમાં છેદે.
(6) ∠BC’A’ = ∠BCA રચીને C માંથી પસાર થતી અને CAને સમાંતર રેખા દોરો, જે BAP A’માં છે.
આથી ∆ A’BC એ માગેલ માપ મુજબનો ∆ ABC ને સમરૂપ હોય તેવો ત્રિકોણ છે અને ∆ ABC ની બાજુઓ ∆ ABC ની અનુરૂપ બાજુઓને \(\frac{3}{4}\) પ્રમાણમાં છે.
યથાર્થતાઃ
∆ BB4Cમાં, B3C’ || B4C .
∆ BB3C’ ~ ∆ BB4C
\(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{BB}_{3}}{\mathrm{BB}_{4}}=\frac{3}{4}\)
∆ BCAમાં, C’A’ || CA
∆ BC’A’~ ∆ BCA
\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{A}^{\prime} \mathrm{C}^{\prime}}{\mathrm{AC}}\) ………….(2)
(1) અને (2) પરથી,
\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{A}^{\prime} \mathrm{C}^{\prime}}{\mathrm{AC}}=\frac{3}{4}\)

પ્રશ્ન 6.
BC = 7 સેમી,∠B = 45, ∠A = 105° હોય તેવો ત્રિકોણ ABC દોરો. પછી એવા ત્રિકોણની રચના કરો કે જેની બાજુઓ ∆ ABCની અનુરૂપ બાજુઓથી \(\frac{4}{3}\) ગણી હોય.
ઉત્તર:
કૃત્ય:
BC = 7 સેમી, ∠B = 45 અને ∠A = 105° હોય તેવો ∆ ABC રચવો. ત્યારબાદ ∆ ABCને સમરૂપ હોય તેવો બીજો ત્રિકોણ રચવો, જેની બાજુઓ ∆ ABCની અનુરૂપ બાજુઓથી \(\frac{4}{3}\) ગણી હોય.
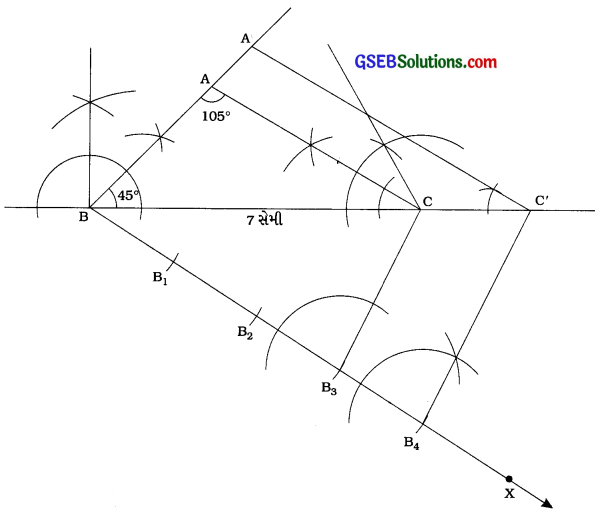
રચનાના મુદ્દા :
(1) BC = 7 સેમી, ∠B = 45° અને ∠C = 30° (∠C = 180° -∠A – ∠B) હોય તેવો ∆ ABC રચો.
(2) BCના જે અર્ધતલમાં બિંદુ A છે તેનાથી વિરુદ્ધ અર્ધતલમાં કિરણ BX દોરો જેથી ∠CBX લઘુકોણ થાય.
(3) BB1 = B1B2 = B2B3 = B3B4 થાય તેવાં ચારે બિંદુઓ B1, B2, B3 અને B4 ને BX પર અંકિત કરો.
(4) B3C જોડો.
(5) ∠BB4C’ = ∠BB3C રચીને B4 માંથી પસાર થતી અને B3Cને સમાંતર રેખા દોરો, જે લંબાવેલ BCને C’ માં છેદે.
(6) ∠BCA’ = ∠BCA રચીને C માંથી પસાર થતી અને CA ને સમાંતર રેખા દોરો, જે લંબાવેલ BA ને A માં છેદે.
આથી ∆ ABC’ એ માગેલ માપ મુજબનો ∆ ABC ને સમરૂપ હોય તેવો ત્રિકોણ છે અને ∆ ABCની બાજુઓ ∆ ABCની અનુરૂપ બાજુઓથી \(\frac{4}{3}\) ગણી છે.
યથાર્થતા:
∆ BB4C’માં, B3C || B4C’
∆ BB4C’ ~ ∆ BB3C
\(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{BB}_{4}}{\mathrm{BB}_{3}}=\frac{4}{3}\) ……. (1)
∆ BC’Aમાં, CA || C’A’
∆ BC’A’ ~ ∆ BCA
\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{A}^{\prime} \mathrm{C}^{\prime}}{\mathrm{AC}}\) ….. (2)
(1) અને (2) પરથી,
\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{A}^{\prime} \mathrm{C}^{\prime}}{\mathrm{AC}}=\frac{4}{3}\)

પ્રશ્ન 7.
4 સેમી અને 3 સેમી લંબાઈની (કર્ણ સિવાયની) બાજુવાળા કાટકોણ ત્રિકોણની રચના કરો. પછી આ ત્રિકોણની બાજુઓને અનુરૂપ તે બાજુઓથી \(\frac{5}{3}\) ગણી બાજુવાળા ત્રિકોણની રચના કરો.
ઉત્તર:
કૃત્ય:
AB = 3 સેમી, ∠B = 90° અને BC = 4 સેમી હોય તેવો ∆ ABC રચવો. ત્યારબાદ ∆ ABC ને સમરૂપ હોય તેવો બીજો ત્રિકોણ રચવો, જેની બાજુઓ ∆ ABCની અનુરૂપ બાજુઓથી \(\frac{5}{3}\) ગણી હોય.
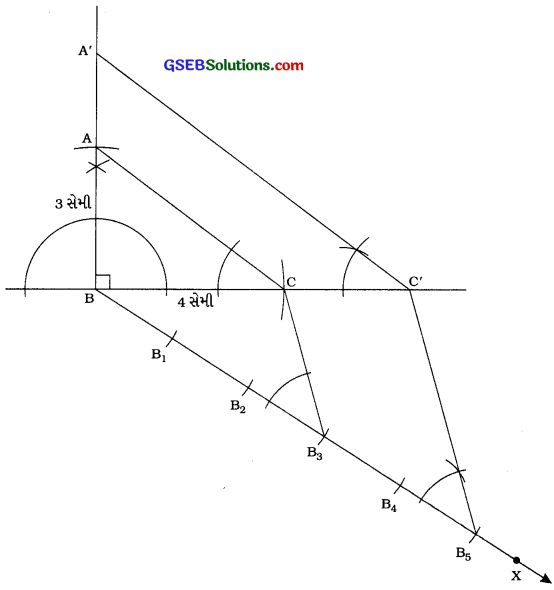
રચનાના મુદ્દા:
(1) AB = 3 સેમી, ∠B = 90° અને BC = 4 સેમી હોય તેવો ∆ ABC રચો.
(2) BC ના જે અર્ધતલમાં બિંદુ A છે તેનાથી વિરુદ્ધ અર્ધતલમાં કિરણ BX દોરો, જેથી ∠CBX લઘુકોણ થાય.
(3) BB1 = B1B2 = B2B3 = B3B4 = B4B5 થાય તેવાં પાંચ બિંદુઓ B1, B2, B3, B4 અને B5 ને BX પર અંકિત કરો.
(4) B5C જોડો.
(5) ∠BB5C’ = ∠BB3C રચીને B5 તુમાંથી પસાર થતી અને B3C ને સમાંતર રેખા દોરો, જે લંબાવેલ BC ને C’માં છે.
(6) ∠BC’A’ = ∠BCA રચીને C માંથી પસાર થતી અને CA ને સમાંતર રેખા દોરો, જે લંબાવેલ BAને A’માં છે.
આથી ∆ A’BC માગેલ માપ મુજબનો ∆ ABCને સમરૂપ હોય તેવો ત્રિકોણ છે અને ∆ ABC ની બાજુઓ ∆ ABCની અનુરૂપ બાજુઓથી \(\frac{5}{3}\) ગણી છે.
યથાર્થતા :
∆ BB5C’માં, B3C || B5C’
∆ BB5C’ ~ ∆ BB3C
\(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{BB}_{5}}{\mathrm{BB}_{3}}=\frac{5}{3}\) ………… (1)
∆ BC’Aમાં, CA || C’A’
∆ BC’A’ ~ ∆ BCA
\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{A}^{\prime} \mathrm{C}^{\prime}}{\mathrm{AC}}\) …………… (2)
(1) અને (2) પરથી,
\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{A}^{\prime} \mathrm{C}^{\prime}}{\mathrm{AC}}=\frac{5}{3}\)