GSEB Solutions Class 10 Maths Chapter 12 વર્તુળ સંબંધિત ક્ષેત્રફળ Ex 12.3

Gujarat Board GSEB Solutions Class 10 Maths Chapter 12 વર્તુળ સંબંધિત ક્ષેત્રફળ Ex 12.3 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 10 Maths Chapter 12 વર્તુળ સંબંધિત ક્ષેત્રફળ Ex 12.3

નોંધઃ ઉલ્લેખ કર્યો ન હોય, તો π = \(\frac{22}{7}\) લો.

પ્રશ્ન 1.
જો PQ = 24 સેમી, PR = 7 સેમી અને વર્તુળનું કેન્દ્ર છે હોય, તો આપેલ આકૃતિમાં દર્શાવેલ રંગીન પ્રદેશનું ક્ષેત્રફળ શોધો.

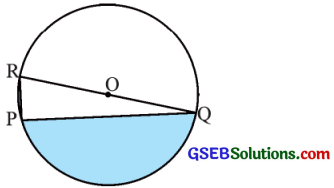
ઉત્તર:
અહીં, એ વર્તુળનું કેન્દ્ર છે.
RQ એ વ્યાસ છે તથા ∠RPG એ અર્ધવર્તુળનો ખૂણો છે.
∠RPQ = 90°
∆ RPQમાં,
RQ = \(\sqrt{\mathrm{PQ}^{2}+\mathrm{PR}^{2}}\) (પાયથાગોરસ પ્રમેય)
= \(\sqrt{24^{2}+7^{2}}\) સેમી
= \(\sqrt{576+49}\) સેમી
= \(\sqrt{625}\) સેમી
∴ RQ = 25 સેમી
∴ વર્તુળનો વ્યાસ = 25 સેમી
∴ ત્રિજ્યા r = \(\frac{25}{2}\) સેમી
∆ RPQમાં, ∠RPQ = 90°
∴ ∆ RPQનું ક્ષેત્રફળ = \(\frac{1}{2}\) × PQ × PR
= \(\frac{1}{2}\) × 24 × 7 સેમી²
= 84 સેમી²
રંગીન પ્રદેશનું ક્ષેત્રફળ = અર્ધવર્તુળનું ક્ષેત્રફળ – RPQ નું ક્ષેત્રફળ
= (\(\frac{1}{2}\) π r² – 84) સેમી²

= (\(\frac{1}{2} \times \frac{22}{7} \times \frac{25}{2} \times \frac{25}{2}\) – 84) સેમી²

= (\(\frac{6875}{28}\) – 84) સેમી²

= (\(\frac{6875-2352}{28}\)) સેમી²

= \(\frac{4523}{28}\) સેમી²

આમ, રંગીન પ્રદેશનું ક્ષેત્રફળ \(\frac{4523}{28}\) સેમી² છે.

પ્રશ્ન 2.
જો કેન્દ્રવાળાં બે સમકેન્દ્રી વર્તુર્થોની ત્રિજ્યા અનુક્રમે 7 સેમી અને 14 સેમી તથા ∠AOC = 40° હોય, તો આપેલ આકૃતિમાં દર્શાવેલ રંગીન પ્રદેશનું ક્ષેત્રફળ શોધો.

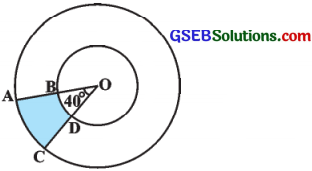
ઉત્તર:
લઘુવૃત્તાંશ OAC માટે, ત્રિજ્યા r = 14 સેમી અને θ = 40°.
લધુવૃત્તાંશ OBCનું ક્ષેત્રફળ = \(\frac{\theta}{360}\) πr²
= \(\frac{40}{360}\) × π × 14 × 14 સેમી²
= \(\frac{196}{9}\) π સેમી²

લઘુવૃત્તાંશ ORD માટે, ત્રિજ્યા r = 7 સેમી અને θ = 40°
લધુવૃત્તાંશ OBDનું ક્ષેત્રફળ = \(\frac{\theta}{360}\) πr²
= \(\frac{40}{360}\) × π × 7 × 7 સેમી²
= \(\frac{49}{9}\) π સેમી²
રંગીન પ્રદેશનું ક્ષેત્રફળ = લઘુવૃત્તાંશ OACનું ક્ષેત્રફળ – લઘુવૃત્તાંશ OBDનું ક્ષેત્રફળ
= (\(\frac{196}{9} \pi-\frac{49}{9} \pi\)) સેમી²

= π (\(\frac{196}{9}-\frac{49}{9}\)) સેમી²

= \(\frac{22}{7} \times \frac{147}{9}\) સેમી²

= \(\frac{154}{3}\) સેમી²
આમ, રંગીન પ્રદેશનું ક્ષેત્રફળ \(\frac{154}{3}\) સેમી² છે.

પ્રશ્ન 3.
14 સેમી બાજુવાળા ચોરસ ABCDમાં જો અર્ધવર્તુળો APP અને BPC આવેલાં હોય, તો આપેલ આકૃતિમાં દર્શાવેલ રંગીન પ્રદેશનું ક્ષેત્રફળ શોધો.

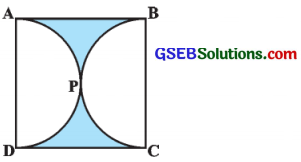
ઉત્તર:
ABCD એ 14 સેમી બાજુવાળો ચોરસ છે.
ચોરસ ABCDનું ક્ષેત્રફળ = (બાજુ)²
= (14)² સેમી²
= 196 સેમી²

AD અને BC વ્યાસવાળાં બે અર્ધવર્તુળો માટે, દરેક અર્ધવર્તુળની ત્રિજ્યા r = \(\frac{\mathrm{AD}}{2}=\frac{14}{2}\) સેમી = 7 સેમી બે અર્ધવર્તુળોનું કુલ ક્ષેત્રફળ = 2 (\(\frac{1}{2}\) πr²)
= πr²
= \(\frac{22}{7}\) × 7 × 7 સેમી
= 154 સેમી²
રંગીન પ્રદેશનું ક્ષેત્રફળ = ચોરસ ABCDનું ક્ષેત્રફળ – બે અર્ધવર્તુળોનું કુલ ક્ષેત્રફળ
= (196 – 154) સેમી² = 42 સેમી²
આમ, રંગીન પ્રદેશનું ક્ષેત્રફળ 42 સેમી² છે.

પ્રશ્ન 4.
12 સેમી બાજુવાળા સમભુજ ત્રિકોણ OABના શિરોબિંદુ oને કેન્દ્ર તરીકે અને ત્રિજ્યા 6 સેમી લઈ, વર્તુળાકાર ચાપ દોર્યું છે. આપેલ આકૃતિમાં દર્શાવેલ રંગીન પ્રદેશનું ક્ષેત્રફળ શોધો.

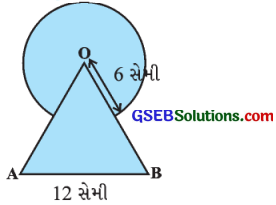
ઉત્તર:
સમભુજ ત્રિકોણ AB માટે, બાજુ a = 12 સેમી
સમભુજ ∆ OAB નું ક્ષેત્રફળ = \(\frac{\sqrt{3}}{4}\) a²
= \(\frac{\sqrt{3}}{4}\) (12)² સેમી²
= 36√3 સેમી²
O કેન્દ્રવાળા વર્તુળ માટે, ત્રિજ્યા r = 6 સેમી
વર્તુળનું ક્ષેત્રફળ = πr²
= \(\frac{22}{7}\) × 6 × 6 સેમી²
= \(\frac{792}{7}\) સેમી²

ત્રિકોણ અને વર્તુળમાં સામાન્ય હોય તેવો પ્રદેશ એ લઘુવૃત્તાંશ છે.
જેને માટે ત્રિજ્યા r = 6 સેમી અને θ = 60° (સમબાજુ ત્રિકોણનો ખૂણો) છે.
લઘુવૃત્તાંશનું ક્ષેત્રફળ = \(\frac{\theta}{360}\) × πr²
= \(\frac{60}{360}\) × \(\frac{22}{7}\) × 6 × 6 સેમી²
= \(\frac{132}{7}\) સેમી²
હવે, રંગીન પ્રદેશનું ક્ષેત્રફળ = ∆ OABનું ક્ષેત્રફળ + O કેન્દ્રવાળા વર્તુળનું ક્ષેત્રફળ – લઘુવૃત્તાંશનું ક્ષેત્રફળ
= (36√3 + \(\frac{792}{7}\) – \(\frac{132}{7}\)) સેમી²
= (36√3 + \(\frac{660}{7}\)) સેમી²
આમ, રંગીન પ્રદેશનું ક્ષેત્રફળ (36√3 + \(\frac{660}{7}\)) સેમી² છે.

પ્રશ્ન 5.
આપેલ આકૃતિમાં દર્શાવ્યા પ્રમાણે 4 સેમી બાજુવાળા ચોરસના પ્રત્યેક ખૂણે 1 સેમી ત્રિજ્યાવાળા વર્તુળનો ચતુર્થાંશ ભાગ કપાયેલો છે તથા 2 સેમી વ્યાસવાળું એક વર્તુળ પણ કાપેલું છે. ચોરસના બાકીના ભાગનું ક્ષેત્રફળ શોધો.

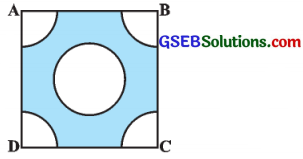
ઉત્તર:
ચોરસ ABCD માટે, બાજુ a = 4 સેમી
ચોરસ ABCDનું ક્ષેત્રફળ = a²
= (4)² સેમી²
= 16 સેમી²
ચોરસના ચારેય ખૂણેથી કાપેલ પ્રત્યેક ચતુર્થાશ માટે ત્રિજ્યા, r = 1 સેમી
ચાર ચતુર્થાશનું કુલ ક્ષેત્રફળ = 4 (\(\frac{1}{4}\) π r²)
= \(\frac{22}{7}\) × 1 × 1 સેમી²
= \(\frac{22}{7}\) સેમી²

મધ્યમાંથી કાપેલ વર્તુળ માટે વ્યાસ = 2 સેમી હોવાથી ત્રિજ્યા r = 1 સેમી
મધ્યમાંથી કાપેલ વર્તુળનું ક્ષેત્રફળ = πr \(\frac{22}{7}\)
= \(\frac{22}{7}\) × 1 × 1 સેમી²
= \(\frac{22}{7}\) સેમી²

ચોરસ ABCDના બાકીના ભાગનું ક્ષેત્રફળ = ચોરસ ABCDનું ક્ષેત્રફળ – ચાર ચતુર્થાશનું કુલ ક્ષેત્રફળ – મધ્યમાંથી કાપેલ વર્તુળનું ક્ષેત્રફળ
= (16 – \(\frac{22}{7}\) – \(\frac{22}{7}\)) સેમી²
= \(\frac{68}{7}\) સેમી²
આમ, આપેલ ચોરસના બાકીના ભાગનું ક્ષેત્રફળ 8 સેમી છે.

પ્રશ્ન 6.
આપેલ આકૃતિમાં દર્શાવ્યા પ્રમાણે ટેબલના એક 32 સેમી ત્રિજ્યાવાળા વર્તુળાકાર આવરણના વચ્ચેના ભાગમાં એક સમભુજ ત્રિકોણ ABC છોડી બાકીના ભાગમાં ભાત બનાવી છે. આ ભાતનું ક્ષેત્રફળ શોધો.

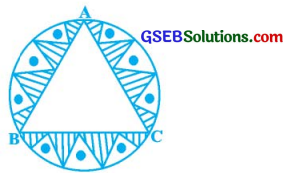
ઉત્તર:
∆ ABC સમભુજ ત્રિકોણ હોવાથી વર્તુળની જીવાઓ AB, BC અને CA સમાન છે અને તેથી AB, BC અને CAને અનુરૂપ લઘુવૃત્તખંડ પણ સમાન અને સમક્ષેત્ર છે. આપણે BCને અનુરૂપ લઘુવૃત્તખંડનું ક્ષેત્રફળ શોધીએ.

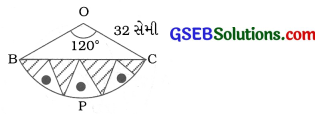
ધારો કે, વર્તુળનું કેન્દ્ર 0 છે. આથી OB = OC = 32 સેમી અને ∠BOC = θ = \(\frac{360^{\circ}}{3}\)= 120°.
લઘુવૃત્તાંશ BPC માટે, ત્રિજ્યા r = 32 સેમી અને લઘુવૃત્તાંશનો ખૂણો θ = 120°
લઘુવૃત્તાંશ OBPCનું ક્ષેત્રફળ = \(\frac{\theta}{360}\) × πr²
= \(\frac{120}{360} \times \frac{22}{7}\) × 32 × 32 સેમી²
= \(\frac{22528}{21}\) સેમી²

∆ OBCના ક્ષેત્રફળ માટે, r = 32 સેમી;
\(\frac{\theta}{2}=\frac{120^{\circ}}{2}\) = 60°;
sin \(\frac{\theta}{2}\) = sin 60° = \(\frac{\sqrt{3}}{2}\) અને cos \(\frac{\theta}{2}\) = cos 60° = \(\frac{1}{2}\)

∆ OBCનું ક્ષેત્રફળ = sing \(\frac{\theta}{2}\) cos \(\frac{\theta}{2}\) r²
= \(\frac{\sqrt{3}}{2} \times \frac{1}{2}\) × 32 × 32 સેમી²
= \(\left(\frac{22528}{21}-256 \sqrt{3}\right)\) સેમી²

આથી લઘુવૃત્તખંડ BPCનું ક્ષેત્રફળ = લઘુવૃત્તાંશ OPBCનું ક્ષેત્રફળ – ∆ OBCનું ક્ષેત્રફળ
= (8528 – 25643) સેમી

ભાતનું ક્ષેત્રફળ = 3 × લઘુવૃત્તખંડ BPCનું ક્ષેત્રફળ
= 3 \(\left(\frac{22528}{21}-256 \sqrt{3}\right)\)0 સેમી²
= \(\left(\frac{22528}{7}-768 \sqrt{3}\right)\) સેમી²
આમ, આપેલ ભાતનું ક્ષેત્રફળ \(\left(\frac{22528}{7}-768 \sqrt{3}\right)\) સેમી છે.

પ્રશ્ન 7.
આપેલ આકૃતિમાં 14 સેમી બાજુવાળો ચોરસ ABCD છે. પ્રત્યેક વર્તુળ બાકીનાં ત્રણ વર્તુળોમાંથી બે વર્તુળને બહારથી સ્પર્શે તેમ A, B, C અને D કેન્દ્રવાળાં ચાર વર્તુળ દોર્યા છે. દર્શાવેલા રંગીન પ્રદેશનું ક્ષેત્રફળ શોધો.

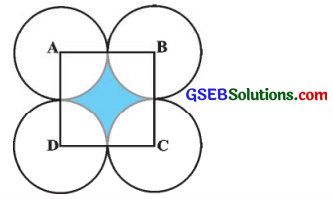
ચોરસ ABCD માટે, બાજુ a = 14 સેમી
ચોરસ ABCDનું ક્ષેત્રફળ = a²
= (14)² સેમી²
= 196 સેમી²
A, B, C અને D કેન્દ્રવાળાં ચાર વર્તુળો પૈકી પ્રત્યેક વર્તુળ બાકીનાં ત્રણ વર્તુળોમાંથી બે વર્તુળોને બહારથી સ્પર્શે છે.
આથી પ્રત્યેક વર્તુળની ત્રિજ્યા ચોરસ ABCDની બાજુ કરતાં અડધી થાય.
આથી દરેક વર્તુળની ત્રિજ્યા = \(\frac{14}{2}\) સેમી = 7 સેમી
રંગીન પ્રદેશ એ ચોરસ ABCDમાંથી ચાર ચતુર્થાશ દૂર કરવાથી મળતો પ્રદેશ છે.
ABCDનાં શિરોબિંદુઓ પર દોરેલ પ્રત્યેક ચતુર્થાશ માટે, ત્રિજ્યા r = 7 સેમી.
ચાર ચતુર્થાશનું કુલ ક્ષેત્રફળ = 4 × (\(\frac{1}{4}\) π r²)
= π r²
= \(\frac{22}{7}\) × 7 × 7 સેમી²
= 154 સેમી²
રંગીન પ્રદેશનું ક્ષેત્રફળ = ચોરસ ABCDનું કુલ ક્ષેત્રફળ – ચાર ચતુર્થાશનું કુલ ક્ષેત્રફળ
= (196 – 154) સેમી²
= 42 સેમી²
આમ, રંગીન પ્રદેશનું ક્ષેત્રફળ 42 સેમી છે.

પ્રશ્ન 8.
આપેલ આકૃતિમાં દોડમાર્ગનું નિરૂપણ કરેલું છે. તેના ડાબા અને જમણા છેડા અર્ધવર્તુળાકાર છે. અંદરના બે સમાંતર રેખાખંડ વચ્ચેનું અંતર 60 મી છે અને તે પ્રત્યેકની લંબાઈ 106 મી છે. જો માર્ગ 10 મી પહોળો હોય, તો
(i) માર્ગની અંદરની ધારનું ચારેય તરફનું અંતર શોધો.
(ii) માર્ગનું ક્ષેત્રફળ શોધો.

ઉત્તર:

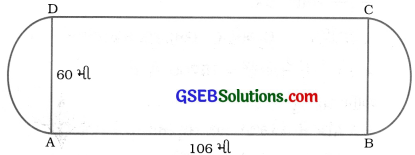
દોડમાર્ગનો અંદરની તરફનો ભાગ બે રેખાખંડ AB અને CD તથા બે અર્ધવર્તુળ AD અને BC દ્વારા ઘેરાયેલ બંધ આકૃતિ રચે છે.
દરેક રેખાખંડની લંબાઈ 106 મી છે તથા દરેક અર્ધવર્તુળનો વ્યાસ અંદરના બે સમાંતર રેખાખંડ AB અને CD વચ્ચેના અંતર જેટલો, એટલે કે, 60 મી છે.
60 મી વ્યાસવાળા દરેક અર્ધવર્તુળની લંબાઈ =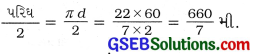
માર્ગની અંદરની ધારનું ચારેય તરફનું અંતર = AB + CD + 2 × દરેક અર્ધવર્તુળની લંબાઈ
= (106 + 106 + 2 × \(\frac{660}{7}\)) મી

= \(\left(\frac{742+742+1320}{7}\right)\) મી

= \(\frac{2804}{7}\) મી

આકૃતિમાં દર્શાવ્યા મુજબ દોડમાર્ગ 106 મી × 10 મી માપના બે લંબચોરસ PQRS અને XYZW તથા બંને તરફ બે અર્ધવર્તુળોના તફાવત દ્વારા બનેલ છે.
લંબચોરસ PQRSનું ક્ષેત્રફળ = લંબાઈ × પહોળાઈ
= (106 × 10) મી²
= 1060 મી²
બે લંબચોરસનું કુલ ક્ષેત્રફળ = (2 × 1060) મી²
= 2120 મી²
હવે, RW = 60 મી
∴ SZ = SR + RW + WZ
= (10 + 60 + 10) મી = 80 મી
આથી SRWZ વિસ્તારનું ક્ષેત્રફળ = SZ વ્યાસવાળા અર્ધવર્તુળનું ક્ષેત્રફળ – RW વ્યાસવાળા અર્ધવર્તુળનું ક્ષેત્રફળ
= \(\frac{\pi \mathrm{R}^{2}}{2}-\frac{\pi r^{2}}{2}\);
જ્યાં, R = \(\frac{\mathrm{SZ}}{2}\) = 40 મી અને r = \(\frac{\text { RW }}{2}\) = 30 મી
= \(\frac{\pi}{2}\left(\mathrm{R}^{2}-r^{2}\right)\)
= \(\frac{\pi}{2}\left(40^{2}-30^{2}\right)\) મી²
= \(\frac{22}{7 \times 2}\) (1600 – 900) મી²
= \(\frac{11}{7}\) × 700 મી²
= 1100 મી²
આથી બંને તરફનાં બે અર્ધવર્તુળોના તફાવત દ્વારા બનતા પ્રદેશોનું ? કુલ ક્ષેત્રફળ = (2 × 1100) મી²
= 2200 મી²
દોડમાર્ગનું કુલ ક્ષેત્રફળ = બે લંબચોરસનું કુલ ક્ષેત્રફળ + બંને તરફનાં અર્ધવર્તુળોનો તફાવત દ્વારા બનતા પ્રદેશોનું
કુલ ક્ષેત્રફળ = (2120 + 2200) મીત² = 4320 મી²
આમ, દોડમાર્ગની અંદરની ધારનું ચારેય તરફનું અંતર \(\frac{2804}{7}\) મી છે તથા દોડમાર્ગનું કુલ ક્ષેત્રફળ 4320 મી² છે.

પ્રશ્ન 9.
આપેલ આકૃતિમાં બે કેન્દ્રવાળા વર્તુળના બે વ્યાસ AB અને CD પરસ્પર લંબ છે અને નાના વર્તુળનો વ્યાસ OD છે. જો OA = 7 સેમી હોય, તો દર્શાવેલ રંગીન પ્રદેશનું ક્ષેત્રફળ શોધો.

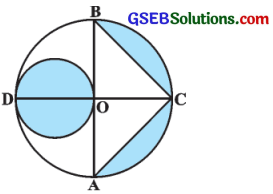
ઉત્તર:
અહીં, OA, OB, OC તથા CD એ મોટા વર્તુળની ત્રિજ્યાઓ છે તથા OA = 7 સેમી
∴ OA = OB = OC = OD = 7 સેમી
હવે, AB = OA + OB = (7 + 7) સેમી = 14 સેમી
વળી, AB ⊥ CD
∴ CO ⊥ AB
∆ ABCનું ક્ષેત્રફળ = \(\frac{1}{2}\) × AB × CO
= (\(\frac{1}{2}\) × 14 × 7) સેમી²
= 49 સેમી²

AB વ્યાસવાળા અર્ધવર્તુળનું ક્ષેત્રફળ = \(\frac{1}{2}\) πr²
= \(\frac{1}{2}\) × \(\frac{22}{7}\) × 7 × 7 સેમી²
= 77 સેમી²
આથી મોટા વર્તુળના બે વૃત્તખંડનું કુલ ક્ષેત્રફળ = અર્ધવર્તુળનું ક્ષેત્રફળ – ∆ ABCનું ક્ષેત્રફળ
= (77 – 49) સેમી² = 28 સેમી²
OD વ્યાસવાળા નાના વર્તુળ માટે, ત્રિજ્યા r = \(\frac{\mathrm{OD}}{2}=\frac{7}{2}\) સેમી
નાના વર્તુળનું ક્ષેત્રફળ = πr²
= \(\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\) સેમી²
= 38.5 સેમી²

આથી રંગીન પ્રદેશનું કુલ ક્ષેત્રફળ = (28 + 38.5) સેમી² = 66.5 સેમી²
આમ, રંગીન પ્રદેશનું ક્ષેત્રફળ 66.5 સેમી² છે.

પ્રશ્ન 10.
એક સમભુજ ત્રિકોણ ABCનું ક્ષેત્રફળ 17320.5 સેમી² છે. ત્રિકોણની બાજુની લંબાઈથી અડધી ત્રિજ્યાવાળા અને પ્રત્યેક શિરોબિંદુ કેન્દ્ર હોય તેવાં વર્તુળ દોર્યા છે. (જુઓ આકૃતિ) દર્શાવેલ રંગીન પ્રદેશનું ક્ષેત્રફળ શોધો. (π = 3.14 અને √3 = 1.73205 લો.)

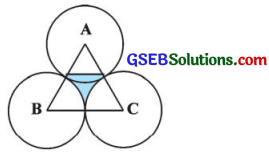
ઉત્તર:
સમભુજ ત્રિકોણ ABCની બાજુની લંબાઈ ધારો કે 4 સેમી છે.
સમભુજ ત્રિકોણ ABCનું ક્ષેત્રફળ = \(\frac{\sqrt{3}}{4}\) a²
∴ 17320.5 = \(\frac{1.73205}{4}\) × a²
a² = 40000
∴ a = 200 સેમી
આમ, ∆ ABCની દરેક બાજુનું માપ 200 સેમી છે.
∴ ∆ ABCના દરેક શિરોબિંદુ પર દોરેલ વર્તુળની ત્રિજ્યા r = \(\frac{200}{2}\) સેમી = 100 સેમી
શિરોબિંદુ A પર દોરેલ વર્તુળનો વૃત્તાંશ કે જે ∆ ABCના અંદરના ભાગમાં સમાયેલ છે.
તેના માટે, ત્રિજ્યા r = 100 સેમી અને વૃત્તાંશનો ખૂણો θ = 60° (સમભુજ ત્રિકોણનો ખૂણો)
લઘુવૃત્તાંશનું ક્ષેત્રફળ = \(\frac{\theta}{360}\) × π r²
= \(\frac{60}{360}\) × 3.14 × 100 × 100 સેમી²
= \(\frac{15700}{3}\) સેમી²
તે જ રીતે, શિરોબિંદુ B અને C પર દોરેલા વર્તુળના વૃત્તાંશ કે જે ∆ ABCના અંદરના ભાગમાં સમાયેલ છે, તે દરેકનું ક્ષેત્રફળ \(\frac{15700}{3}\) સેમી² થાય.
∴ શિરોબિંદુ A, B અને C પરના ત્રણ લઘુવૃત્તાંશનું કુલ ક્ષેત્રફળ = 3 × \(\frac{15700}{3}\) સેમી² = 15700 સેમી²
રંગીન પ્રદેશનું ક્ષેત્રફળ = ∆ ABCનું ક્ષેત્રફળ – ત્રણ લઘુવૃત્તાંશનું ક્ષેત્રફળ
= (17320.5 – 15700) સેમી²
= 1620.5 સેમી²
આમ, રંગીન પ્રદેશનું ક્ષેત્રફળ 1620.5 સેમી² છે.

પ્રશ્ન 11.
એક ચોરસ હાથરૂમાલ પર 7 સેમી ત્રિજ્યાવાળી નવ વર્તુળાકાર ભાત બનાવી છે. (જુઓ આકૃતિ) હાથરૂમાલના બાકીના ભાગનું ક્ષેત્રફળ શોધો.

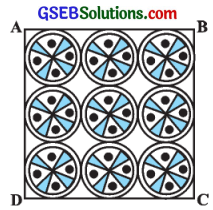
ઉત્તર:
નવ વર્તુળાકાર ભાત પૈકી દરેક ભાત માટે, ત્રિજ્યા r = 7 સેમી.
નવ વર્તુળાકાર ભાતનું કુલ ક્ષેત્રફળ = 9πr²
= 9 × \(\frac{22}{7}\) × 7 × 7 સેમી²
= 1386 સેમી²
દરેક વર્તુળાકાર ભાતનો વ્યાસ = (2 × 7) સેમી = 14 સેમી
ચોરસ ABCDની દરેક બાજુની લંબાઈ = (3 × 14) સેમી = 42 સેમી
ચોરસ ABCDનું ક્ષેત્રફળ = (બાજુ)²
= (42)² સેમી²
= 1764 સેમી
હાથરૂમાલના બાકીના ભાગનું ક્ષેત્રફળ = ચોરસ ABCDનું ક્ષેત્રફળ – નવ વર્તુળાકાર ભાતનું કુલ ક્ષેત્રફળ
= (1764 – 1386) સેમી² = 378 સેમી²
આમ, હાથરૂમાલના બાકીના ભાગનું ક્ષેત્રફળ 378² સેમી છે.

પ્રશ્ન 12.
આપેલ આકૃતિમાં દર્શાવેલ ચતુર્થાશ OACBનું કેન્દ્ર 0 છે અને ત્રિજ્યા 3.5 સેમી છે. જો આD = 2 સેમી હોય, તો,
(i) ચતુર્ભાશ (AC)નું ક્ષેત્રફળ શોધો.
(ii) દર્શાવેલ રંગીન પ્રદેશનું પ્ર ક્ષેત્રફળ શોધો.

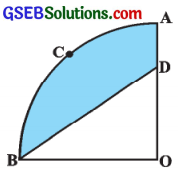
ઉત્તર:
ચતુર્ભાશ OACB માટે, ત્રિજ્યા r = 3.5 સેમી = \(\frac{7}{2}\) સેમી
ચતુર્ભાશ OACBનું ક્ષેત્રફળ = \(\frac{1}{4}\) (π r²)
= \(\frac{1}{4} \times \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\) સેમી²
= \(\frac{77}{8}\) સેમી²
OACB એ વર્તુળનું ચતુર્ભાશ હોવાથી,
∠BOA = ∠BOD = 90°
∆ BODમાં, ∠BOD = 90°
∆ BODનું ક્ષેત્રફળ = \(\frac{1}{2}\) × BO × OD

= (\(\frac{1}{2}\) × \(\frac{7}{2}\) × 2) સેમી²
= \(\frac{7}{2}\) સેમી²
રંગીન પ્રદેશનું ક્ષેત્રફળ = ચતુર્ભાશ ACBનું ક્ષેત્રફળ – ∆ BODનું ક્ષેત્રફળ

= (\(\left(\frac{77}{8}-\frac{7}{2}\right)\)) સેમી²

= (\(\frac{77-28}{8}\)) સેમી² = \(\frac{49}{8}\) સેમી²

આમ, ચતુર્થાશ OACBનું ક્ષેત્રફળ \(\frac{77}{8}\) સેમી² છે તથા રંગીન પ્રદેશનું ક્ષેત્રફળ \(\frac{49}{8}\) સેમી² છે.

પ્રશ્ન 13.
આપેલ આકૃતિમાં, એક વર્તુળના ચતુર્થાશ OPBની અંતર્ગત ચોરસ GABC છે. જો OA = 20 સેમી હોય, તો દર્શાવેલ રંગીન પ્રદેશનું ક્ષેત્રફળ શોધો. (π = 3.14 લો.)

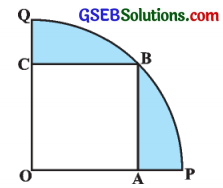
ઉત્તર:
ચોરસ ABC માટે, બાજુ a = OA = 20 સેમી
ચોરસ આABCનું ક્ષેત્રફળ = a²
= (20)² સેમી²
= 400 સેમી²
∆ OABમાં, ∠A = 90° અને OA = AB = 20 સેમી
આથી OB = \(\sqrt{\mathrm{OA}^{2}+\mathrm{AB}^{2}}\) (પાયથાગોરસ પ્રમેય)
= \(\sqrt{20^{2}+20^{2}}\)
= \(\sqrt{2 \times 20^{2}}\) = 20√2 સેમી
આથી ચતુર્ભાશ OPBOની ત્રિજ્યા r = 20√2 સેમી.
ચતુર્થાશ OPBQનું ક્ષેત્રફળ = \(\frac{1}{4}\) (π r²)
= \(\frac{1}{4}\) × 3.14× 20√2 × 20√2 સેમી²
= 628 સેમી²
રંગીન પ્રદેશનું ક્ષેત્રફળ = ચતુર્થાશ OPBQ નું ક્ષેત્રફળ – ચોરસ (ABCનું ક્ષેત્રફળ
= (628 – 400) સેમી²
= 228 સેમી²
આમ, રંગીન પ્રદેશનું ક્ષેત્રફળ 228 સેમી² છે.

પ્રશ્ન 14.
O કેન્દ્રવાળા, 21 સેમી અને 7 સેમી બે ત્રિજ્યાવાળાં બે સમકેન્દ્રી વર્તુળના ચાપ અનુક્રમે AB અને CD છે. (જુઓ આકૃતિ) જો ∠AOB = 30° હોય, તો દર્શાવેલ રંગીન પ્રદેશનું ક્ષેત્રફળ શોધો.

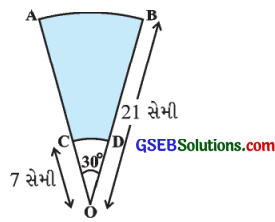
ઉત્તર:
મોટા વૃત્તાંશ આAB માટે, ત્રિજ્યા r₁ = 21 સેમી અને θ = 30°
નાના વૃત્તાંશ OCD માટે, ત્રિજ્યા r₂ = 7 સેમી અને θ = 30°
રંગીન પ્રદેશનું ક્ષેત્રફળ = મોટા વૃત્તાંશ OABનું ક્ષેત્રફળ – નાના વૃત્તાંશ OCDનું ક્ષેત્રફળ

આમ, રંગીન પ્રદેશનું ક્ષેત્રફળ \(\frac{308}{3}\) સેમી² છે.

પ્રશ્ન 15.
આપેલ આકૃતિમાં, ABC એ 14 સેમી ત્રિજ્યાવાળા વર્તુળનો ચતુર્થાશ છે. BCને વ્યાસ તરીકે લઈ વર્તુળ દોરવામાં આવ્યું છે, તો દર્શાવેલ રંગીન પ્રદેશનું ક્ષેત્રફળ શોધો.

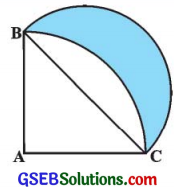
ઉત્તર:
ચતુર્થાશ ABCની ચાપ BC પર એક બિંદુ P લો. ચતુર્થાશ ABC માટે, ત્રિજ્યા r = 14 સેમી.
ચતુથશે ABCનું ક્ષેત્રફળ = \(\frac{1}{4}\) (π r²)
= \(\frac{1}{4} \times \frac{22}{7}\) × 14 × 14 સેમી²
= 154 સેમી²

∆ BACમાં, ∠A = 90°
∴ ∆ BACનું ક્ષેત્રફળ = \(\frac{1}{2}\) × AB × AC
= 98 સેમી²

વૃત્તખંડ BPCનું ક્ષેત્રફળ = ચતુર્થાશ ABCનું ક્ષેત્રફળ – ∆ BACનું ક્ષેત્રફળ
= (154- 98) સેમી² = 56 સેમી²

∆ BACમાં, ∠A = 90° અને AB = AC = 14 સેમી
આથી BC = \(\sqrt{\mathrm{AB}^{2}+\mathrm{AC}^{2}}\) (પાયથાગોરસ પ્રમેય)
= \(\sqrt{14^{2}+14^{2}}\)
= \(\sqrt{2 \times 14^{2}}\)
= 14√2 સેમી

આથી BC વ્યાસવાળા અર્ધવર્તુળની ત્રિજ્યા r = \(\frac{\mathrm{BC}}{2}=\frac{14 \sqrt{2}}{2}\) સેમી = 7√2 સેમી

અર્ધવર્તુળનું ક્ષેત્રફળ = \(\frac{1}{2}\) (π r²)
= \(\frac{1}{2} \times \frac{22}{7} \times 7 \sqrt{2} \times 7 \sqrt{2}\)
= 154 સેમી²

રંગીન પ્રદેશનું ક્ષેત્રફળ = અર્ધવર્તુળનું ક્ષેત્રફળ – વૃત્તખંડ BPCનું ક્ષેત્રફળ
= (154 – 56) સેમી² = 98 સેમી²
આમ, રંગીન પ્રદેશનું ક્ષેત્રફળ 98 સેમી² છે.

પ્રશ્ન 16.
આપેલ આકૃતિમાં, 8 સેમી ત્રિજ્યાવાળાં બે વર્તુળના સામાન્ય ચતુર્થાશની ભાતના પ્રદેશના ક્ષેત્રફળની ગણતરી કરો.

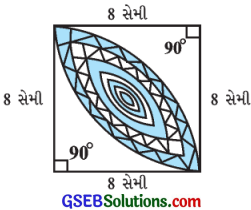
ઉત્તર:
પ્રત્યેક ચતુર્ભાશ માટે ત્રિજ્યા r = 8 સેમી
બે ચતુર્થાશનું કુલ ક્ષેત્રફળ = 2 × \(\frac{1}{4}\) (π r²)
= 2 × \(\frac{1}{4}\) × \(\frac{22}{7}\) × 8 × 8 સેમી²
= \(\frac{704}{7}\) સેમી²

ચોરસનું ક્ષેત્રફળ = (બાજુ)²
= (8)² સેમી²
= 64 સેમી²

ભાતના પ્રદેશનું ક્ષેત્રફળ = બે ચતુર્થાશનું કુલ ક્ષેત્રફળ – ચોરસનું ક્ષેત્રફળ
= (\(\frac{704}{7}-64\)) સેમી²
= (\(\frac{704-448}{7}\)) સેમી²
= \(\frac{256}{7}\) સેમી²
આમ, ભાતના પ્રદેશનું ક્ષેત્રફળ \(\frac{256}{7}\) સેમી² છે.