GSEB Solutions Class 10 Maths Chapter 13 પૃષ્ઠફળ અને ઘનફળ Ex 13.4

Gujarat Board GSEB Solutions Class 10 Maths Chapter 13 પૃષ્ઠફળ અને ઘનફળ Ex 13.4 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 10 Maths Chapter 13 પૃષ્ઠફળ અને ઘનફળ Ex 13.4

(જો નું મૂલ્ય આપેલ ન હોય, તો π = \(\frac{22}{7}\) લો.)

પ્રશ્ન 1.
14 સેમી ઊંચાઈવાળા પીવાના પાણીનો પ્યાલો શંકુના આડછેદના આકારનો છે. બંને વર્તુળાકાર છેડાના વ્યાસ 4 સેમી અને 2 સેમી હોય, તો આ પ્યાલાની ક્ષમતા શોધો.
ઉત્તર:
આપેલ શંકુના આડછેદ આકારના પ્યાલા માટે, મોટી ત્રિજ્યા r₁ = \(\frac{4}{2}\) સેમી = 2 સેમી,
નાની ત્રિજ્યા r₂ = \(\frac{2}{2}\) સેમી = 1 સેમી અને ઊંચાઈ h = 14 સેમી
પ્યાલાની ક્ષમતા = શંકુના આડછેદનું ઘનફળ
= \(\frac{1}{3}\) πh (r₁² + r₂² + r₁ r₂)
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × 14 (2² + 1² + 2 × 1) સેમી³
= \(\frac{1}{3}\) × 44 × 7 સેમી
= \(\frac{308}{3}\) સેમી³
= 102\(\frac{2}{3}\) સેમી³
આમ, આપેલ પ્યાલાની ક્ષમતા 102\(\frac{2}{3}\) સેમી છે.

પ્રશ્ન 2.
એક શંકુના આડછેદની તિર્યક ઊંચાઈ 4 સેમી છે તથા તેના વર્તુળાકાર છેડાની પરિમિતિ (પરિઘ) 18 સેમી અને 6 સેમી છે, તો શંકુના આડછેદની વક્રસપાટીનું ક્ષેત્રફળ શોધો.
ઉત્તર:
આપેલ શંકુના આડછેદ માટે, તિર્યક ઊંચાઈ l = 4 સેમી, મોટા વર્તુળાકાર છેડાનો પરિઘ C₁ = 18 સેમી અને નાના વર્તુળાકાર છેડાનો પરિઘ C₂ = 6 સેમી
શંકુના આડછેદની વક્રસપાટીનું ક્ષેત્રફળ = πl (r₁ + r₂)
= \(\frac{l}{2}\) (2πr₁ + 2πr₂)
= \(\frac{l}{2}\) (C₁ + C₂)
= \(\frac{4}{2}\) (18 + 6) સેમી²
= 48 સેમી²
આમ, આપેલ શંકુના આડછેદની વક્રસપાટીનું ક્ષેત્રફળ 48 સેમી² છે.

પ્રશ્ન 3.
એક તુર્કી ટોપીનો આકાર શંકુના આડછેદ જેવો છે. (જુઓ આકૃતિ) જો તેની ખુલ્લી બાજુની ત્રિજ્યા 10 સેમી અને ઉપરની બાજુના વર્તુળની ત્રિજ્યા 4 સેમી હોય અને તિર્યક ઊંચાઈ 15 સેમી હોય, તો તેને બનાવવા માટે વપરાતા કાપડનું ક્ષેત્રફળ શોધો.

ઉત્તર:
શંકુના આડછેદ આકારની તુર્કી ટોપી માટે, મોટી ત્રિજ્યા r₁ = 10 સેમી, નાની ત્રિજ્યા r₂ = 4 સેમી અને તિર્યક ઊંચાઈ l = 15 સેમી
તુર્કી ટોપી બનાવવા માટે વપરાતા કાપડનું ક્ષેત્રફળ = શંકુના આડછેદની વક્ર સપાટીનું ક્ષેત્રફળ + નાના વર્તુળાકાર છેડાનું ક્ષેત્રફળ
= πl (r₁ + r₂) + πr₂²
= π[l(r₁ + r₂) + r₂²]
= \(\frac{22}{7}\) [15(10 + 4) + 4²] સેમી²
= \(\frac{22}{7}\) × 226 સેમી²
= \(\frac{4972}{7}\) સેમી²
= 710 \(\frac{2}{7}\) સેમી²
આમ, તુર્કી ટોપી બનાવવા માટે વપરાતા કાપડનું ક્ષેત્રફળ 710 \(\frac{2}{7}\) સેમી² થાય.

પ્રશ્ન 4.
એક વાસણ એક ધાતુની શીટમાંથી બનાવવામાં આવ્યું છે. તે ઉપરથી ખુલ્લું છે અને શંકુના આડછેદ જેવા આકારનું છે. તેની ઊંચાઈ 16 સેમી તથા બંને અંત્ય વર્તુળોની નીચેની અને ઉપરની ત્રિજ્યા અનુક્રમે 8 સેમી અને 20 સેમી છે. દૂધથી સંપૂર્ણ ભરેલા વાસણમાં ₹ 20 પ્રતિ લિટર કિંમતવાળા આ વાસણમાં સમાઈ શકતા દૂધની કિંમત શોધો. આ વાસણ બનાવવા માટે વપરાયેલ ધાતુની શીટની કિંમત ₹ 8 પ્રતિ 100 સેમીગ્ના દરે શોધો. (π = 3.14 લો.)
ઉત્તર:
શંકુના આડછેદ આકારના વાસણ માટે, મોટી ત્રિજ્યા r₁ = 20 સેમી, નાની ત્રિજ્યા r₂ = 8 સેમી અને ઊંચાઈ h = 16 સેમી.
તિર્યક ઊંચાઈ l = \(\sqrt{h^{2}+\left(r_{1}-r_{2}\right)^{2}}\)
= \(\sqrt{16^{2}+(20-8)^{2}}\) સેમી
= \(\sqrt{256+144}\) સેમી
= \(\sqrt{400}\) સેમી
= 20 સેમી
સંપૂર્ણ ભરેલા વાસણમાં સમાતું દૂધ = વાસણની ક્ષમતા
= શંકુના આડછેદનું ઘનફળ
= \(\frac{1}{3}\) πh (r₁² + r₂² + r₁r₂) સેમી³
= \(\frac{1}{3}\) × 3.14 × 16 × (20² + 8² + 20 × 8) સેમી³
= \(\frac{1}{3}\) × 3.14 × 16 × (400 + 64 + 160) સેમી³
= \(\frac{1}{3}\) × 3.14 × 16 × 624 સેમી³
= 10449.92 સેમી³
= \(\frac{10449.92}{1000}\) લિટર (1 લિટર = 1000 સેમી)
= 10.45 લિટર

1 લિટર દૂધની કિંમત = ₹ 20
∴ 10.45 લિટર દૂધની કિંમત = ₹ (10.45 x 20) = ₹ 209
વાસણ બનાવવામાં વપરાયેલ ધાતુની શીટનું ક્ષેત્રફળ = શંકુના આડછેદની વક્ર સપાટીનું ક્ષેત્રફળ + તેના નાના છેડાનું ક્ષેત્રફળ
= πl (r₁ + r₂) + πr₂²
= π[l (r₁ + r₂) + r₂²]
= 3.14 [20 (20 + 8) + 8²] સેમી²
= 3.14 [560 + 64] સેમી²
= 1959.36 સેમી²
100 સેમી² ધાતુની શીટની કિંમત = ₹ 8
1959.36 સેમી² ધાતુની શીટની કિંમત = ₹ \(\left(\frac{1959.36 \times 8}{100}\right)\)
= ₹ 156.75
આમ, સંપૂર્ણ ભરેલા વાસણમાં સમાતા દૂધની કિંમત ૨209 થાય અને વાસણ બનાવવા માટે વપરાયેલ ધાતુની શીટની કિંમત ₹ 156.75 થાય.

પ્રશ્ન 5.
ધાતુના લંબવૃત્તીય શંકુની ઊંચાઈ 20 સેમી તથા શિરોકોણ 60° છે. પાયાને સમાંતર સમતલથી તેના ઊંચાઈના બે સમાન ભાગ થાય તે રીતે કાપવામાં આવ્યો છે. જો આડછેદનું \(\frac{1}{16}\) સેમી વ્યાસવાળા તાર સ્વરૂપમાં રૂપાંતર કરવામાં આવે, તો તારની લંબાઈ શોધો.
ઉત્તર:

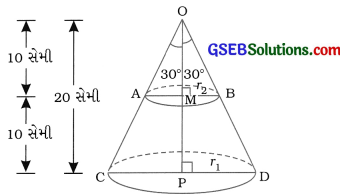
અહીં, 20 સેમી ઊંચાઈ અને 60નો શિરોકોણ ધરાવતા લંબવૃત્તીય શંકુ OCDને પાયાને સમાંતર સમતલથી ઊંચાઈના બે સમાન ભાગ થાય તે રીતે કાપવામાં આવ્યો છે.
એટલે કે, શિરોબિંદુ 0થી 10 સેમી અંતરેથી કાપીને શંકુ OAB તથા શંકુનો આડછેદ ACDB મેળવવામાં આવ્યા છે.
શંકુ આABના મધ્યમાં ઊભો છેદ મૂકવાથી ∆ OMB મળે, જેમાં OM = 10 સેમી, MB = r₂ અને
∠MOB = = \(\frac{60^{\circ}}{2}\) = 30°.
∆ OMBમાં, ∠M = 90°
∴ tan O = \(\frac{\mathrm{MB}}{\mathrm{OM}}\)

∴ tan 30° = \(\frac{r_{2}}{10}\)

∴ \(\frac{1}{\sqrt{3}}=\frac{r_{2}}{10}\)

∴ r₂ = \(\frac{10}{\sqrt{3}}\) સેમી

તે જ રીતે, શંકુ OCDના મધ્યમાં ઊભો છેદ મૂકવાથી ∆ OPD મળે જેમાં OP = 20 સેમી, PD = r₁, અને ∠POD = 30°.
∆ OPDમાં, ∠P = 90°
tan O = \(\frac{\mathrm{PD}}{\mathrm{OP}}\)
tan 30° = \(\frac{r_{1}}{20}\)
\(\frac{1}{\sqrt{3}}=\frac{r_{1}}{20}\)
r₁ = \(\frac{20}{\sqrt{3}}\) સેમી
આથી શંકુના આડછેદ ACDBમાં, મોટી ત્રિજ્યા r₁ = \(\frac{20}{\sqrt{3}}\) સેમી,
નાની ત્રિજ્યા r₂ = \(\frac{10}{\sqrt{3}}\) સેમી ી અને ઊંચાઈ h = MP = 10 સેમી
શંકુના આડછેદ ACDBનું ઘનફળ = \(\frac{1}{3}\) πh (r₁ + r₂ + r₁r₂)
= \(\frac{1}{3} \times \frac{22}{7} \times 10\left(\frac{400}{3}+\frac{100}{3}+\frac{200}{3}\right)\) સેમી³
= \(\frac{1}{3} \times \frac{22}{7} \times 10 \times \frac{700}{3}\) સેમી³
= \(\frac{22000}{9}\) સેમી³
શંકુના આડછેદ ACDBનું જે તારમાં રૂપાંતર કરવામાં આવે છે તે તાર માટે, ત્રિજ્યા r = = \(\frac{1}{32}\) સેમી અને ઊંચાઈ (લંબાઈ) = h સેમી.
તારનું ઘનફળ = શંકુના આડછેદનું ઘનફળ
πr² h = \(\frac{22000}{9}\)
\(\frac{22}{7} \times \frac{1}{32} \times \frac{1}{32} \times h=\frac{22000}{9}\)
h = \(\frac{22000 \times 7 \times 32 \times 32}{9 \times 22}\) સેમી
h = 796444 સેમી
h = 7964.4 મી
આમ, રૂપાંતર કરીને બનાવવામાં આવતા તારની લંબાઈ 7964.4 મી થાય.