Gujarat Board Statistics Class 11 GSEB Solutions Chapter 2 सूचना का प्रस्तुतीकरण Ex 2.1 Textbook Exercise Questions and Answers.
Gujarat Board Textbook Solutions Class 11 Statistics Chapter 2 सूचना का प्रस्तुतीकरण Ex 2.1
प्रश्न 1.
एक विस्तार में रहनेवाले 30 परिवारों में बालकों की संख्या निम्नलिखित है । इस सूचना पर से योग्य आवृत्ति वितरण तैयार कीजिए ।

उत्तर :
यहाँ परिवार में बालकों की संख्या यह असतत (खंडित) चर है ! बालकों की महत्तम संख्या 3 और न्यूनतम संख्या 0 है।
इसलिए दी गई अवर्गीकृत सूचना का विस्तार R = 3 – 0 = 3 होगा इसलिए बालको को संख्या दर्शाता हुआ असतत (खंडित) आवृत्ति वितरण निम्न प्राप्त होगा ।
50 परिवारों में बालकों की संख्या दर्शाता हुआ असतत (खंडित) आवृति वितरण

प्रश्न 2.
एक कार्यालय में सेवारत 60 कर्मचारियों का संपूर्ण वर्ष में आयु का लेखा निम्नानुसार किया गया है । इस सूचना से 5 की वर्ग-लम्बाई लेकर आवृत्ति वितरण तैयार कीजिए ।

उत्तर : सूचना का विस्तार R = महत्तम मूल्य – न्यूनतम मूल्य
= 58 – 21 ∴ R = 37
∴ वर्गलंबाई 5 दी गई है ।
वर्गों की संख्या = \(\frac{\mathrm{R}}{\mathrm{C}}\) ∴ K = \(\frac{37}{5}\) = 7.4 = 7
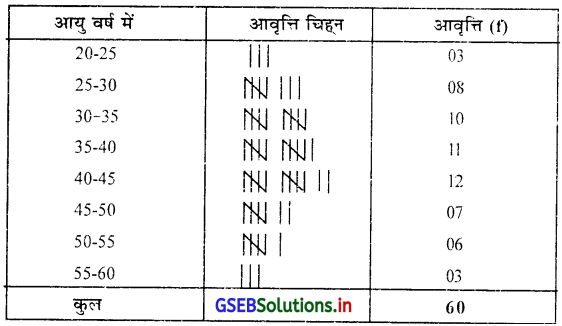
60 कर्मचारियों का संपूर्ण वर्ष में आयु प्रदर्शित करता निवारक सतत आवृत्ति वितरण
![]()
प्रश्न 3.
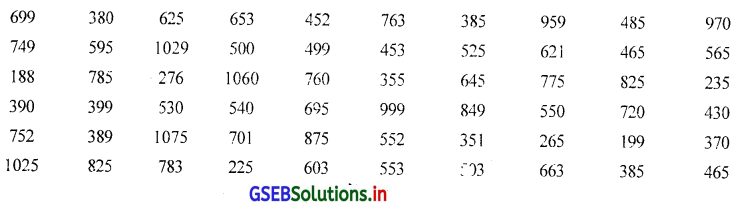
मोबाईल बनानेवाली एक कंपनी द्वारा अंतिम 60 दिनों में उत्पादित मोबाईल की संख्या निम्नानुसार है । उसे 10 वर्गों में विभाजीत करो । उस पर से ‘से कम’ और ‘से अधिक’ प्रकार के आवृत्ति वितरण की तुलना करो ।
उत्तर :
सूचना को 10 वर्गों में विभाजीत करना है । सूचना में महत्तम अवलोकन 1075 और न्यूनतम अवलोकन 188 है ।
विस्तार R = महत्तम अवलोकन – न्यूनतम अवलोकन
1075 – 199 = 876
∴ वर्ग लंबाई C = \(\frac{\mathrm{R}}{\mathrm{K}}=\frac{876}{10}\) = 87.6
∴ गणना की सरलता के लिए वर्गलंबाई C = 100 लेने पर प्रथम वर्ग 100 – 199 जिसमें लघुतम अवलोकन 199 का समावेश होता है और अंतिम वर्ग 1000 से 1099 रखेंगे जिसमें महत्तम अवलोकन 1075 का समावेश होता है ।
60 दिन के दौरान मोबाईल का उत्पादन दर्शाता हुआ अनिवारक प्रकार का सतत (अखंडित) आवृत्ति वितरण
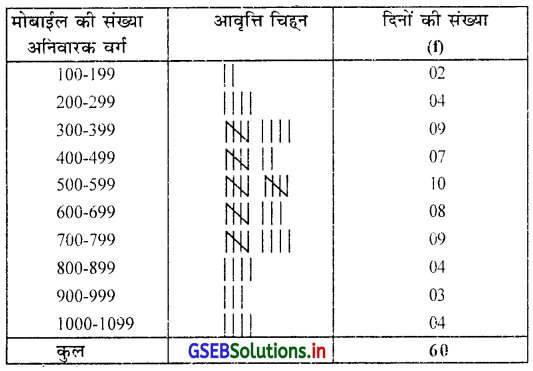
‘से कम’ और ‘से अधिक’ प्रकार के आवृत्ति वितरण प्राप्त करने के लिए सीमाबिंदु प्राप्त करेंगे ।
प्रथम वर्ग का अधः सीमाबिंदु = 99.5 और उसीमा बिंदु 199.5 प्राप्त होगा निवारक वर्ग

60 दिनों में उत्पादित मोबाईल का ‘से कन’ प्रकार का संचयी आवृत्ति वितरण उर्ध्व सीमाबिंदु ‘से कम’
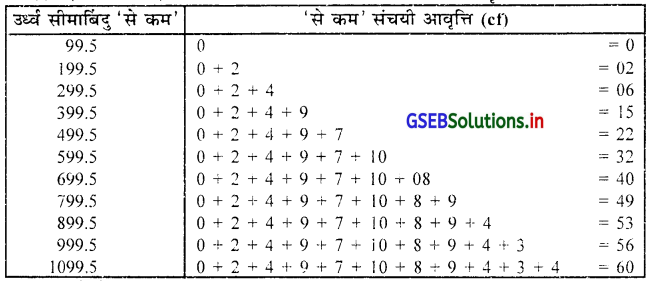
60 दिनों में उत्पादित मोबाईल का ‘से अधिक’ प्रकार का संचयी आवृत्ति वितरण
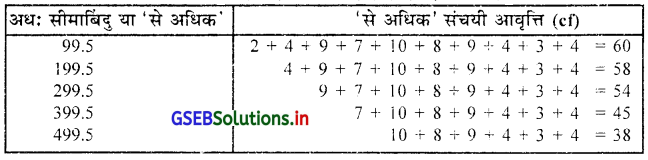

प्रश्न 4.
निम्न आवृत्ति वितरण के लिए प्रत्येक वर्ग की वर्गलंबाई और मध्यकिंमत ज्ञात करके वितरण लिखो।

उत्तर :
आवृत्ति वितरण अनिवारक प्रकार का 1 है इसलिए उसे निवारक वर्ग में बदलेंगे ।
दूसरा वर्ग की निम्नसीमा 100 और प्रथम वर्ग की उच्च सीमा 99 है ।
इसलिए दूसरे वर्ग की अधः सीमाबिंदु = \(\frac{100+99}{2}\) = 99.5 और उर्ध्वसीमा बिंदु = 99.5 – 200 वर्ग लंबाई = 299.5 दूसरा वर्ग की सीमाबिंदुओं 99.5 – 299.5 और उस पर से प्रथम वर्ग के सीमा बिंदुओं – 0.5 – 99.5 होगा ।
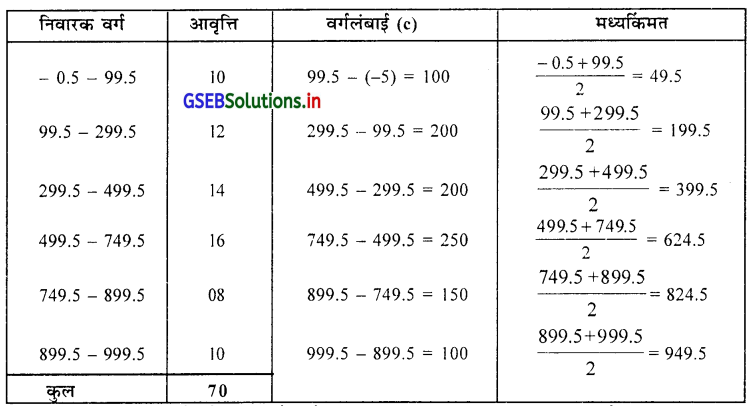
![]()
प्रश्न 5.
निम्न आवृत्ति वितरण पर से ‘से कम’ और ‘से अधिक’ संचयी आवृत्ति वितरण प्राप्त करो ।

उत्तर :
यहाँ असतत (खंडित) आवृत्ति वितरण दिया है इसलिए ‘से कम’ और ‘से अधिक’ प्रकार का असतत (खंडित) संचयी आवृत्ति वितरण निम्नानुसार प्राप्त करेंगे ।
से कम’ प्रकार का असतत (खंडित) आवृत्ति वितरण
| x या उससे कम भूलों की संख्या | से कम’ संचयी आवृत्ति (cf) |
| 0 | 140 = 140 |
| 1 | 140 + 110 = 250 |
| 2 | 140 + 110 + 120 = 370 |
| 3 | 140 + 110 + 120 + 30 = 400 |
‘से अधिक’ प्रकार का संचयी आवृत्ति वितरण
| x या उससे अधिक भूलों की संख्या (≥ x) | ‘से अधिक’ संचयी आवृत्ति (cf) |
| 0 | 30 + 120 + 110 + 140 = 400 |
| 1 | 30 + 120 + 110 = 260 |
| 2 | 30 + 120 = 150 |
| 3 | 30 = 30 |
प्रश्न 6.
निम्न सूचना पर से अनिवारक सतत आवृत्ति वितरण की रचना करो ।

उत्तर :
अधः सीमाबिंदु दिये गए है और वर्ग लंबाई 5 है।
प्रथम वर्ग की अधःसीमा = 44.5 + 0.5 = 45
प्रथम वर्ग की उर्ध्वसीमा = 49.5 – 0.5 = 49
∴ प्रथम वर्ग 45-49 प्राप्त होगा ।
शेष वर्ग निम्नानुसार प्राप्त करेंगे ।
अनिवारक सतत (अखंडित) आवृत्ति वितरण
| वर्ग | आवृत्ति f |
| 45 – 49 | 500 – 470 = 30 |
| 50 – 54 | 470 – 390 = 80 |
| 55 – 59 | 390 – 290 = 100 |
| 60 – 64 | 290 – 240 = 50 |
| 65 – 69 | 240 – 90 = 150 |
| 70 – 74 | 90 – 10 = 80 |
| 75 – 79 | 10 – 0 = 10 |
| कुल | = 500 |
प्रश्न 7.
निम्न सूचना पर से सतत निवारक आवृत्ति वितरण प्राप्त करो ।

उत्तर :
‘से कम’ प्रकार का आवृत्ति वितरण दिया है । इसलिए प्रथम वर्ग की अधःसीमा = 30 और उर्ध्वसीमा = 35 होगा इसलिए प्रथम वर्ग = 30 – 35 होगा शेष वर्ग और आवृत्ति वितरण
निवारक सतत (अखंडित) आवृत्ति वितरण
| वर्ग | आवृत्ति f |
| 30 – 35 | 17 – 0 = 17 |
| 35 – 40 | 25 – 17 = 08 |
| 40 – 45 | 40 – 25 = 15 |
| 45 – 50 | 48 – 40 = 08 |
| 50 – 55 | 54 – 48 = 06 |
| 55 – 60 | 57 – 54 = 03 |
| 60 – 65 | 59 – 57 = 02 |
| 65 – 70 | 60 – 59 = 01 |
| कुल | = 70 |
![]()
प्रश्न 8.
निम्न सूचना पर से मूल आवृत्ति वितरण प्राप्त करो ।

उत्तर :
मध्यकिमत और वर्ग लंबाई दी गई है इसलिए उस पर से प्रथम वर्ग प्राप्त करेंगे । प्रथम वर्ग अधःसीमा
प्रथम वर्ग की अधःसीमा = मध्यकिंमत – 
= 25 – \(\frac{50}{2}\) = 25 – 25
∴ प्रथम वर्ग की अधःसीमा = 0
वर्गलंबाई प्रथम वर्ग की उर्ध्वसीमा = मध्यकिंमत + 
= 25 + \(\frac{50}{2}\) = 25 + 25 = 50
∴ प्रथम वर्ग 0-50 प्राप्त होगा। प्रथम वर्ग को उर्ध्वसीमा दूसरे वर्ग की अधःसीमा बनेगी इसलिए निवारक प्रकार का आवृत्ति वितरण निम्नानुसार प्राप्त होगा । वर्गलंबाई जोड़ने पर
निवारक प्रकार का सतत (अखंडित) आवृत्ति वितरण
| वर्ग | आवृत्ति f |
| 0 – 50 | 10 |
| 50 – 160 | 30 |
| 160 – 300 | 40 |
| 300 – 500 | 60 |
| 500 – 800 | 80 |
| 800 -1000 | 30 |
| कुल | 250 |
नोंध : प्रत्येक अधःसीमा उससे उपरी वर्ग की उर्ध्वसीमा होगी। उसमें वर्गलंबाई जोड़ने पर शेष वर्ग की उर्वसीमा प्राप्त होती है।
प्रश्न 9.
वर्ष दौरान शहर में हुए दुर्घटनाओं की संख्या निम्नानुसार है । उस पर से अनिवारक प्रकार का सतत (अखंडित) आवृत्ति वितरण प्राप्त करो।

उत्तर :
दुर्घटनाओं की संख्या यह सतत (अखंडित) आवृत्ति वितरण है । दो क्रमिक मध्यकिंमत के बीच अंतर 10 है ।
∴ C = 10
वर्गलंबाई (c) प्रथम वर्ग की अधःसीमा = मध्यकिमत – 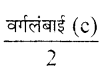
= 11.5 – \(\frac{10}{2}\) = 11.5 – 5
∴ प्रथम वर्ग की अधःसीमा = 6.5
प्रथम वर्ग की उध्वंसीमा = मध्यांकमत + 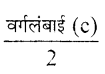
= 11.5 + \(\frac{10}{2}\) = 11.5 + 5 = 16.5
∴ प्रथम वर्ग 6.5-16.5 प्राप्त होगा निवारक वर्ग को अनिवारक सतत (अखंडित) आवृत्ति वितरण में बदलने के लिए अधःसोमाबिंदु में 0.5 जोड़ने पर और उर्ध्वसीमाबिंदु में से 0.5 घटाने पर अनिवारक प्रथम वर्ग 6.5 + 0.5 = 7 ऊर्ध्वसीमा 16.5 – 0.5 = 16 । प्रथम अनिवारक वर्ग 7 से 16 प्राप्त होगा । प्रत्येक वर्ग में वर्गलबाई जोड़ने पर निम्न अनिवारक प्रकार का आवृत्ति वितरण प्राप्त होगा ।
वर्ष दौरान शहर में हुई दुर्घटनाओं की संख्या दर्शाता हुआ अनिवारक सतत (खंडित) आवृत्ति वितरण
| वर्ग | आवृत्ति |
| 7 – 16 | 160 |
| 17 – 26 | 120 |
| 27 – 36 | 43 |
| 37 – 46 | 40 |
| 47 – 56 | 02 |
| कुल | 365 |
![]()
प्रश्न 10.
निम्न दिए गए आवृत्ति वितरण के सीमाओं पर से सीमाबिंदुओं प्राप्त करके आवृत्ति वितरण लिखो ।

उत्तर :
निवारक वर्ग प्राप्त करने के लिए दूसरा वर्ग की अधः सीमा 1.5 और प्रथम वर्ग की उर्ध्वसीमा 1.475 है इसलिए दूसरा वर्ग
की अधःसीमा बिंदु = \(\frac{1.5+1.475}{2}=\frac{2.975}{2}\) = 1.4875 और उस वर्ग की उर्ध्वसीमा बिंदु = 1.4875 + 0.5 (वर्गलंबाई)
= 1.9875
दूसरा वर्ग 1.4875 – 1.9875 प्राप्त होगा।
प्रथम वर्ग की उर्ध्वसीमा 1.4875 बनेगी । उसमें से वर्गलंबाई 0.5 घटाने पर अधःसीमा 0.9875 प्राप्त होगा। प्रत्येक वर्ग में 0.5 वर्गलंबाई जोडकर वर्ग निम्नानुसार प्राप्त होगा। निवारक आवृत्ति वितरण निम्नानुसार प्राप्त होगा।
| वर्ग | आवृत्ति f |
| 0.9875 – 1.4875 | 5 |
| 1.4875 – 1.9875 | 10 |
| 1.9875 – 2.4875 | 20 |
| 2.4875 – 2.9875 | 20 |
| 2.9875 – 3.4875 | 10 |
| 3.4875 – 3.9875 | 05 |
| कुल | 70 |