Gujarat Board Statistics Class 11 GSEB Solutions Chapter 2 सूचना का प्रस्तुतीकरण Ex 2 Textbook Exercise Questions and Answers.
Gujarat Board Textbook Solutions Class 11 Statistics Chapter 2 सूचना का प्रस्तुतीकरण Ex 2
विभाग – A
निम्न दिए गए विकल्प में से सही विकल्प का चयन करके लिखिए ।
प्रश्न 1.
निम्न में से कौन-सा चल असतत (खंडित) है ?
(A) व्यक्ति की उँचाई
(B) वस्तु का वजन
(C) मेदान का क्षेत्रफल
(D) प्रतिपरिवार में बालको की संख्या
उत्तर :
(D) प्रतिपरिवार में बालको की संख्या
प्रश्न 2.
निम्न में से कौन-सा सतत (अखंडित) चल है ?
(A) पुस्तक में प्रति पन्ने भूल की संख्या
(B) कार के उत्पादन की संख्या
(C) मार्ग पर दुर्घटनाओं की संख्या
(D) व्यक्ति की मासिक आय
उत्तर :
(D) व्यक्ति की मासिक आय
प्रश्न 3.
वस्तु की दैनिक माँग की अवर्गीकृत सूचना को वर्गीकृत करने की विधि को क्या कहते है ?
(A) गुणात्मक सूचना का वर्गीकरण
(B) संख्यात्मक सूचना का वर्गीकरण
(C) अवर्गीकृत सूचना
(D) बहुविधि वर्गीकरण
उत्तर :
(B) संख्यात्मक सूचना का वर्गीकरण
प्रश्न 4.
किसी एक विस्तार के रहीशों के व्यवसाय और उसके अभ्यास की दी गई सूचना को वर्गीकृत करने की विधि को क्या कहते है ?
(A) कोष्टकरचना
(B) संख्यात्मक सूचना का वर्गीकरण
(C) अवर्गीकृत वितरण
(D) असतत (अखंडित) आवृत्ति वितरण
उत्तर :
(C) अवर्गीकृत वितरण
प्रश्न 5.
सतत (अखंडित) आवृत्ति वितरण में वर्ग की वर्गलंबाई अर्थात् क्या ?
(A) दो क्रमिक अध: सीमाबिंदु की औसत
(B) वर्ग की वर्गसीमाओं की औसत
(C) वर्ग की उर्ध्वसीमाबिंदु और अधः सीमाबिंदुओं के बीच का अंतर
(D) वर्ग की उर्ध्वसीमाबिंदु और अध: सीमाबिंदु की औसत
उत्तर :
(C) वर्ग की उर्ध्वसीमाबिंदु और अधः सीमाबिंदुओं के बीच का अंतर
प्रश्न 6.
किसी एक अवर्गीकृत सूचना का विस्तार 55 है और उसे छ समान वर्गलंबाईवाले वर्गों में विभाजित करना हो तो वर्गलंबाई कितनी होगी ?
(A) 10
(B) 9
(C) 9.17
(D) 10.17
उत्तर :
(A) 10
![]()
प्रश्न 7.
अनिवारक वर्गों 10-19.5, 20-29.5, 30-39.5 है, तो दूसरा वर्ग की निवारक सीमाएँ कौन-सी होगी ?
(A) 19.5 – 29.5
(B) 19.75 – 29.75
(C) 20 – 30
(D) 19-29
उत्तर :
(B) 19.75 – 29.75
प्रश्न 8.
एक असतत (खंडित) चल का मूल्य 0, 1, 2, 3, 4 की आवृत्ति क्रमशः 2, 4, 6, 8, 14 है, तो चल की किंमत 2 के अनुरूप ‘से अधिक’ संचयी आवृत्ति कितनी होगी ?
(A) 28
(B) 12
(C) 34
(D) 6
उत्तर :
(A) 28
प्रश्न 9.
सतत चर (अखंडित) के वर्गों 0-9, 10-19, 20-29, 30-39 है और उसकी आवृत्ति क्रमशः 10, 20, 40, 10 है, तो सीमाबिंदु 295 के अनुरूप ‘से कम’ संचयी आवृत्ति कितनी होगी ?
(A) 30
(B) 50
(C) 70
(D) 80
उत्तर :
(C) 70
प्रश्न 10.
एक सतत (अखंडित) सूचना के लिए वर्गों 1-1.95, 2-2.95, 3-3.95, 4-4.95, 5-5.95 है तो दूसरे वर्ग का अधःसीमा बिंदु कितना ?
(A) 1.995
(B) 2
(C) 2.975
(D) 1.975
उत्तर :
(D) 1.975
प्रश्न 11.
आकृतिओं के लिए निम्न में से कौन-सा विधान सही है ?
विधान 1 : विशाल और बहुविध (जटील) सूचना को सरल और आकर्षक रीति से प्रस्तुत करने की विधि अर्थात् आकृति ।
विधान 2 : सूचना के मुख्य लक्षण अपने आप स्पष्ट बने इस प्रकार का प्रस्तुतीकरण अर्थात् आकृति ।
विधान 3 : सूचना का तुलनात्मक अध्ययन स्पष्ट करता प्रस्तुतीकरण अर्थात् आकृति ।
(A) सिर्फ विधान 1 सत्य
(B) सिर्फ विधान 2 और 3 सत्य
(C) विधान 1, 2 और 3 सत्य
(D) तीनों विधान गलत
उत्तर :
(C) विधान 1, 2 और 3 सत्य
प्रश्न 12.
एक सतत (अखंडित) सूचना के वर्ग 0-99, 100-199, 200-299, 300-399, 400-499 है, तो दूसरा वर्ग की मध्यकिंमत कितनी होगी ?
(A) 149.5
(B) 150
(C) 199.5
(D) 99.5
उत्तर :
(A) 149.5
![]()
प्रश्न 13.
किसी एक कंपनी में कार्यरत कर्मचारियों का कार्यपद, लिंग और वैवाहित स्तर दर्शाती सारणी को …………………………..
(A) सरल सारणी कहते है ।
(B) संख्यात्मक सूचना का वर्गकरण कहते है ।
(C) बहुविध (जटिल) वर्गीकरण कहते है ।
(D) सरल सारणी
उत्तर :
(C) बहुविध (जटिल) वर्गीकरण कहते है ।
प्रश्न 14.
वर्गीकृत सूचना को उपविभागों में प्रस्तुत करने के लिए कौन-सी आकृति उपयोगी है ?
(A) सरल स्तंभाकृति
(B) विभाजित स्तंभाकृति
(C) पासपास (बहुगुणी) स्तंभाकृति
(D) चित्राकृति
उत्तर :
(B) विभाजित स्तंभाकृति
प्रश्न 15.
वर्गीकृत सूचना के उपसूचनाओं की तुलना के लिए कौन-सी आकृति उपयोगी है ?
(A) चित्राकृति
(B) वृत्तांश आकृति
(C) सरल अन्नविभक्त (विभाजित) स्तंभाकृति
(D) विभाजित स्तंभाकृति
उत्तर :
(B) वृत्तांश आकृति
विभाग – B
निम्न प्रश्नों के एक वाक्य में उत्तर दीजिए ।
प्रश्न 1.
असतत (खंडित) चर की परिभाषा दीजिए ।
उत्तर :
जो चर दो अन्तरालों के बीच किसी निश्चित मूल्य को ही धारण करता हो उसे असतत (खंडित) चर कहेंगे ।
प्रश्न 2.
सतत (अखंडित) चर की परिभाषा दीजिए।
उत्तर :
जो चर दो सीमाओं के किसी भी मूल्य को धारण करने में समर्थ हो उसे सतत (अखंडित) चर कहते है ।
प्रश्न 3.
वर्गीकरण अर्थात् क्या ?
उत्तर :
अवर्गीकृत सूचना को संक्षिप्त में और व्यवस्थित स्वरूप में गठित करने की क्रिया को सूचना का वर्गीकरण (classification) कहते है ।
प्रश्न 4.
वर्गीकरण के प्रकार बताइए ।
उत्तर :
वर्गीकरण के मुख्य दो प्रकार है :
- संख्यात्मक सूचना का वर्गीकरण
- गुणात्मक सूचना का वर्गीकरण
प्रश्न 5.
चल के मूल्य की आवृत्ति की परिभाषा दीजिए ।
उत्तर :
चल के मूल्य का पुनरावर्तन दर्शाती संख्या को उस चर मूल्य की आवृत्ति (f) कहते है ।
![]()
प्रश्न 6.
वर्ग की वर्गलंबाई और सूचना का विस्तार दिया हो तब वर्गों की संख्या ज्ञात करने की विधि लिखो ।
उत्तर :
वर्गों की संख्या ज्ञात करने के लिए विस्तार R को वर्गलंबाई से भाग देने पर प्राप्त होता है ।
अर्थात् (वर्गों की संख्या) K = 
प्रश्न 7.
असमान वर्ग लंबाईवाला आवृत्ति वितरण कब बनाना चाहिए ?
उत्तर :
जब अवर्गीकृत सूचना का विस्तार बड़ा हो तब असमान वर्ग लंबाईवाला आवृत्ति वितरण तैयार किया जाता है ।
प्रश्न 8.
संचयी आवृत्ति की परिभाषा दीजिए।
उत्तर :
चल की किंमत और वर्ग की आवृत्ति और उससे कम सभी चर मूल्यों या वर्गों की आवृत्तियों के योग को उस चर मूल्य की संचयी आवृत्ति (Cumulative Frequency) कहते है और उसके वितरण को संचयी आवृत्ति वितरण कहते है ।
प्रश्न 9.
असतत (खंडित) आवृत्ति वितरण के लिए ‘से कम’ प्रकार का संचयी आवृत्ति वितरण पारिभाषित कीजिए।
उत्तर :
असतत (खंडित) आवृत्ति वितरण में दिए गए चर के मूल्य की आवृत्ति एवं उसमें कम सभी चर मूल्यों की आवृत्तियों के योग को उस चर मूल्य की संचयी आवृत्ति कहते है । उसे ‘से कम’ प्रकार का संचयी आवृत्ति वितरण कहते है ।
प्रश्न 10.
सतत (अखंडित) आवृत्ति वितरण के लिए ‘से अधिक’ प्रकार का संचयी आवृत्ति वितरण पारिभाषित कीजिए ।
उत्तर :
सतत आवृत्ति वितरण में अधःसीमा बिन्दु या उससे अधिक मूल्यवाले अवलोकनों से समाविष्ट सभी वर्ग की आवृत्ति के योग की ‘से अधिक’ प्रकार का संचयी आवृत्ति वितरण कहते है । (More than type cumulative frequency distribution)
प्रश्न 11.
वर्ग की मध्यकिंमत ज्ञात करने का सूत्र बताइए ।
उत्तर :
मध्यकिंमत = 
प्रश्न 12.
कोष्टक रचना की परिभाषा दीजिए।
उत्तर :
सूचना के अवलोकनों को वर्गीकरण हेतु निर्देशित स्तरानुसार वर्गीकृत करके उन्हें स्तंभों (vertical) और पंक्तियों (Rows) (Horizontal) में व्यवस्थित रूप से गठित करने की क्रिया को कोष्टक रचना (Tabulation) कहते है ।
![]()
प्रश्न 13.
बहुविध सारणी को पारिभाषित करो।
उत्तर :
एक से अधिक गुणधर्मों के अनुसार रचित सारणी को बहुविध (Manifold Calssification) कहते है ।
प्रश्न 14.
कौन सारणी को (कोष्टक को) श्रेष्ठ सारणी कहते है ?
उत्तर :
सामान्यतः सूचना के उद्देश्य की पूर्ति करे ऐसी सारणी को श्रेष्ठ सारणी कहते है ।
प्रश्न 15.
सूचना के वर्गीकरण की मुख्य मर्यादा क्या है ?
उत्तर :
जब अवलोकनों की संख्या अधिक हो या प्रसार अधिक हो तब वर्गीकरण करने में उलझन पूर्ण बनता है ।
प्रश्न 16.
सांख्यिकी के अभ्यास में आकृतिओं का मुख्य उद्देश्य क्या है ?
उत्तर :
विशाल और जटिल सूचनाओं को आकर्षक और प्रभावशाली रूप से प्रस्तुत करने के लिए आंकडाशास्त्र के अभ्यास में आकृतिओं का उपयोग करने का उद्देश्य है ।
प्रश्न 17.
आकृतिओं के प्रकार बताइए । (Types of Diagrams)
उत्तर :
आकृति के मुख्य तीन प्रकार है :
- एकायामी चित्र (One – dimensional diagram)
- द्वि-आयामी चित्र (Two dimensional diagram)
- चित्राकृति (Pictorial diagram)
प्रश्न 18.
पासपास के (बहुगुणी) दण्डचित्र की आकृति कब खिंची जाती है ?
उत्तर :
जब विविध स्थानों, वस्तुओं के समय के लिए एक से अधिक लक्षणों की सूचना एकत्रित की गई हो तब उस सूचना को आकृति में दर्शाने के लिए पासपास के (बहुगुणी) दण्डचित्र का उपयोग किया जाता है ।
![]()
प्रश्न 19.
विभाजित स्तंभाकृति (दण्डचित्र ) कब खिची जाती है ?
उत्तर :
दी गई सूचना को अलग अलग विभागों में प्रस्तुत करने के लिए विभाजित दण्डचित्र (Differential Bar Diagram) खिंचा जाता है। .
प्रश्न 20.
प्रतिशत विभाजित (अन्तर्विभक्त) दण्डचित्र का मुख्य उद्देश्य बताइए ।
उत्तर :
सरल विभाजित (सरल अन्तर्विभक्त) दण्डचित्र से कुल सूचना का विभागों में विभाजन आकर्षक प्रस्तुत किया जाता है । लेकिन तुलना संभव नहीं बनती । यह मर्यादा को दूर करने के उद्देश्य से प्रतिशत (Percentage Divided Bar Diagram) विभाजित दण्डचित्र का उपयोग किया जाता है।
विभाग – C
निम्न प्रश्नों के उत्तर दीजिए ।
प्रश्न 1.
गुणात्मक सूचना और संख्यात्मक सूचना का अंतर स्पष्ट कीजिए ।
उत्तर :
| गुणात्मक सूचना | संख्यात्मक सूचना |
| (1) चर लक्षण गुणधर्म पर आधारित हो उसे गुणात्मक सूचना कहते है । | (1) यदि सूचना संख्यात्मक रीति से प्राप्त की गई हो तो संख्यात्मक सूचना कहते है । |
| (2) व्यक्तियों को धर्म से दर्शानेवाली सूचना गुणात्मक सूचना है। | (2) विद्यार्थियों की ऊँचाई दर्शानेवाली सूचना के समूह को संख्यात्मक सूचना कहते है । |
प्रश्न 2.
असतत आवृत्ति वितरण की परिभाषा उदाहरण सहित दीजिए।
उत्तर :
चलमूल्य के पुनरावर्तन दर्शाती संख्या को चल मूल्य की आवृत्ति कहते हैं । असतत (खंडित) चल के विविध शक्य मूल्यों के अनुरूप आवृत्ति दर्शाते कोष्टक को असतत (खंडित) आवृत्ति वितरण कहते है । उदाहरण : प्रति परिवार में बालकों की संख्या, पुस्तक में भूलों की संख्या इत्यादि असतत (खंडित) चल के उदाहरण है ।
प्रश्न 3.
सतत (अखंडित) आवृत्ति वितरण की परिभाषा उदाहरण सहित दीजिए।
उत्तर :
यदि सूचना सतत (अखंडित) चल की हो तो चल कीमतों की योग्य संख्या में वर्ग बनाकर उस पर से आवृत्ति प्राप्त की जाती है । इस प्रकार बननेवाली आवृत्ति वितरण को सतत (अखंडित) आवृत्ति वितरण कहा जाता है । कर्मचारियों के वेतन में असमानता अधिक हो तब सतत आवृत्ति वितरण बनाया जाता है ।
प्रश्न 4.
निवारक सतत आवृत्ति वितरण की परिभाषा समझाईए ।
उत्तर :
वर्गलंबाई सूचना के विस्तार के आधार पर से निश्चित करके प्रत्येक वर्ग की वर्गसीमा निश्चित की जाती है। यदि किसी भी वर्ग की उर्ध्वसीमा उसके पश्चाद् के वर्ग की निम्न सीमा बनती हो अर्थात् दोनों समान हो तो उस वर्ग को निवारक वर्ग (Exclusive Class) कहते है । निवारक वर्ग में उर्ध्वसीमा जीतना मूल्य उसके बाद के वर्ग में समाविष्ट किया जाता है। उदा. 50-60 का वर्ग हो तो 50 उसी वर्ग में लेकिन 60 को 50-60 के वर्ग में समाविष्ट नहीं किया जाता । उसे उसके बाद का वर्ग में समाविष्ट किया जाता है ।
प्रश्न 5.
अनिवारक सतत आवृत्ति वितरण की परिभाषा समझाइए ।
उत्तर :
जब असतत (खंडित) अवर्गीकृत सूचना दी हो और विस्तार बड़ा हो तब सामान्यतः अनिवारक सतत आवृत्ति वितरण प्राप्त किया जाता है । किसी भी वर्ग की उर्ध्वसीमा उसके बाद के वर्ग की अधःसीमा न बनती हो अर्थात् दोनों समान न हो तो उसे अनिवारक वर्ग (Inclusive Class) कहते है। अनिवारक वर्ग में अधःसीमा और उर्ध्वसीमा जितना मूल्यवाले अवलोकनों का समावेश उसी वर्ग में होता है । उदा. 30-34 का वर्ग हो तो 34 का समावेश उसी वर्ग में होगा उसका आवृत्तिचिह्न 30-34 के वर्ग में किया जाता है ।
![]()
प्रश्न 6.
अनिवारक सतत (अखंडित) आवृत्ति वितरण के वर्गसीमा पर से वर्ग सीमा बिंदुओं ज्ञात करने का सूत्र लिखिए। उत्तर : किसी भी अनिवारक सतत आवृत्ति वितरण के अधःसीमाबिंदु (Lower Boundary Point) और उर्ध्वसीमा बिंदु (Upper Boundary Point) निम्न सूत्रों द्वारा ज्ञात करेंगे ।
का मूल्य वर्ग का अधःसीमाबिंदु = 
वर्ग का उर्ध्वसीमा बिंदु = 
अथवा
वर्ग का उर्ध्वसीमा बिंदु = अधःसीमा बिंदु + वर्ग लंबाई (C)
प्रश्न 7.
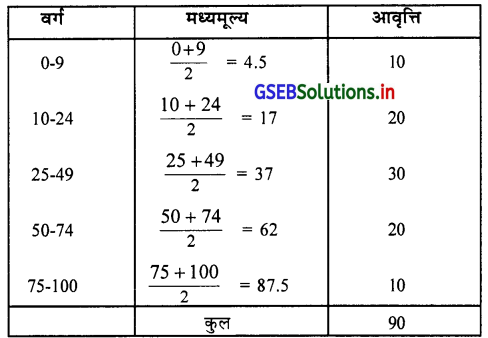
निम्न आवृत्ति वितरण का मध्यमूल्यों (मध्यकिंमतों) को ज्ञात करो ।

उत्तर :
वर्ग का मध्यमूल्य = 
सूत्र का उपयोग करके आवृत्ति वितरण के मध्यमूल्यों को ज्ञात करेंगे ।
प्रश्न 8.
90 उपर्युक्त प्र.7 के आवृत्ति वितरण पर से प्रत्येक वर्ग की वर्गलंबाई ज्ञात करो ।
उत्तर :
प्रत्येक वर्ग की वर्गलंबाई दर्शाता हुआ आवृत्ति वितरण निम्नानुसार प्राप्त करेंगे ।
| वर्ग | वर्गलंबाई | आवृत्ति |
| 0 – 9 | 10 | 10 |
| 10 – 24 | 15 | 20 |
| 25 – 49 | 25 | 30 |
| 50 – 74 | 25 | 20 |
| 75 – 100 | 26 | 10 |
| कुल | 90 |
नोट : आवृत्ति वितरण अनिवारक सतत प्रकार का है इसलिए दोनों सीमा (उर्ध्व और अधः) का समावेश उसी वर्ग में होता है ।
प्रश्न 9.
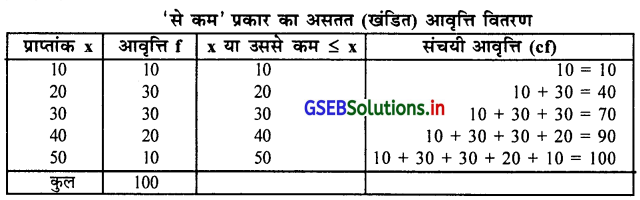
निम्न आवृत्ति वितरण के लिए ‘से कम’ प्रकार का संचयी आवृत्ति वितरण प्राप्त करो ।

उत्तर :
यहाँ असतत (खंडित) चल का आवृत्ति वितरण दिया है इसलिए ‘से कम’ प्रकार का असतत संचयी आवृत्ति वितरण निम्नानुसार प्राप्त करेंगें।
प्रश्न 10.
एक वस्तु की माँग को उत्तम, मध्यम और कमजोर ऐसे तीन वर्गों में विभाजित की जाती है। एक वर्ष का अभ्यास दौरान मालूम हुआ कि 22 सप्ताह के दौरान माँग मध्यम थी । जब कि 18 सप्ताह के दौरान वस्तु की माँग कम थी । उस सूचना को कोष्टक में प्रस्तुत करो ।
उत्तर :
वस्तु की माग प्रदशित सारणी

प्रश्न 11.
निम्न सारणी को पूर्ण करो ।

उत्तर :
गुणधर्म, वर्ष, नंबर प्रदर्शित सारणी

![]()
प्रश्न 12.
निवारक सतत आवृत्ति-वितरण और अनिवारक सतत आवृत्ति वितरण के बीच का अंतर दीजिए ।
उत्तर :
| निवारक सतत आवृत्ति वितरण | अनिवारक सतत आवृत्ति वितरण |
| (1) किसी भी वर्ग की उर्ध्वसीमा उसके पश्चाद् के वर्ग की अधःसीमा हो तो उसे निवारक वर्ग कहते हैं । | (1) जब किसी वर्ग की उर्ध्वसीमा और उसके पश्चाद् के वर्ग की अधःसीमा समान न हो तो उसे अनिवारक वर्ग कहते है। |
| (2) निवारक वर्ग में अधःसीमा जितना अवलोकन को उसी वर्ग में समाविष्ट किया जाता है । जब कि उर्ध्वसीमा का समावेश उसके बाद के वर्ग में होता है । | (2) अनिवारक वर्ग में अधःसीमा और उर्ध्वसीमा दोनों अवलोकन मूल्य का समावेश उसी वर्ग में किया जाता है । |
| (3) उदा. 40-50 के वर्ग में 40 का समावेश 40-50 के वर्ग में जब कि 50 का समावेश उसके बाद का वर्ग 50-60 में होता है । | (3) उदा. 40-49 का वर्ग हो तो 40 और 49 दोनों का समावेश 40-49 वर्ग में होता है । |
प्रश्न 13.
आकृति की मर्यादाएं बताइए।
उत्तर :
आकृति की मर्यादाएँ निम्नलिखित है :
- चित्रों द्वारा सूचना का प्रस्तुतीकरण आंकड़ों द्वारा प्रस्तुत की गई सूचना जितनी विश्वसनीय नहीं होती है ।
- आकृति की पसंदगी उचित रूप से नहीं की गई हो तो समझने में कठिनाई होती है ।
- दृष्टिभ्रम से लोक मानस भ्रमित हो सकता है, आकृति का दुरुपयोग हो सकता है इसलिए मात्र सिमित उपयोग का एक साधन ही बनकर रह जाता है।
- बड़ी व्यापारिक संस्थाओं में विज्ञापन के लिए गलतरूप से आकृति का उपयोग करते है जिससे लोग भ्रमित हो जाते है।
- आकृति द्वारा सूचनाओं का प्रस्तुतीकरण एक सुन्दर माध्यम होने पर भी उससे सचोटता लुप्त हो जाती है । वह एक. अनुमान मात्र ही रहता है, सिर्फ प्राथमिक निष्कर्ष का ही एक साधन मात्र है ।
14.
एकायामी आकृति अर्थात् क्या ? उनके नाम दीजिए ।
उत्तर :
जब दी गई सूचना के किसी एक ही परिमाण को लक्ष में लेकर चित्र बनाया जाय तो उस आवृत्ति को एकायामी आकृति कहते है। एकायामी आकृति निम्नलिखित है : ।
- दण्डचित्र (स्तंभाकृति) (Bar Diagram)
- बहुगुणी दण्डचित्र (Collateral or Multiple Bar Diagram)
- सरल अन्तर्विभक्त दण्ड-चित्र (सरल विभाजित स्तंभाकृति – Simple Divided Bar Diagram)
- प्रतिशत अंतर्विभक्त (प्रतिशत विभाजित) दण्डचित्र (Percentage Divided Bar Diagram)
प्रश्न 15.
द्वि-आयामी आकृति पर संक्षिप्त टिप्पणी लिखो ।
(Two Dimensional Diagram)
उत्तर :
सूचना की मात्र संख्यात्मक रूप से बड़ी या विस्तृत हो तो एकायामी चित्र का उपयोग नहीं किया जा सकता । इस कठिनाई
को दूर करने के लिए द्वि-आयामी आकृतिओं का उपयोग प्रस्तुतीकरण की दृष्टि से अधिक उपयोगी हो सकता है। ऐसे चित्रों में लंबाई और चौड़ाई दोनों माप ध्यान में लिए जाते है । यहाँ कुल मात्रा को आकृति के क्षेत्रफल जितना गिनकर चित्रों को
रेखांकित किया जाता है । परिणामस्वरूप इन में वर्गाकार आयत, वृत्तांश-चित्रों का समावेश किया है ।
प्रश्न 16.
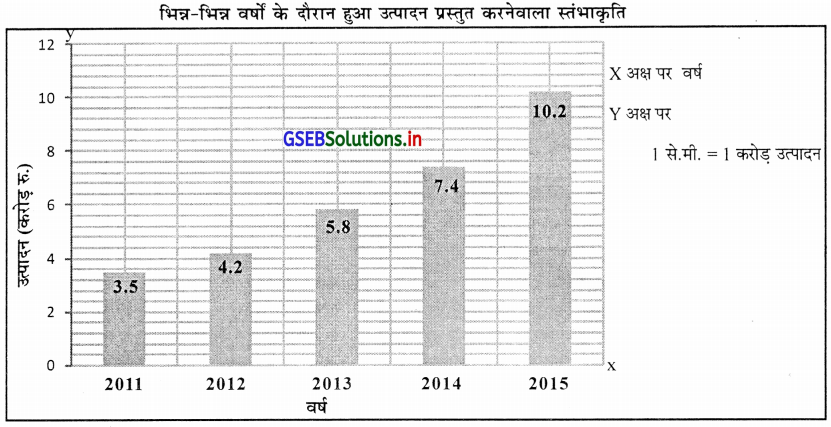
निम्न सूचना को स्तंभाकृति में प्रस्तुत कीजिए ।

यहा X अक्ष पर वर्ष तथा Y अक्ष पर योग्य प्रमाणमाप लेकर उत्पादन (करोड़ रु.) में दर्शायेंगे ।

उत्तर :
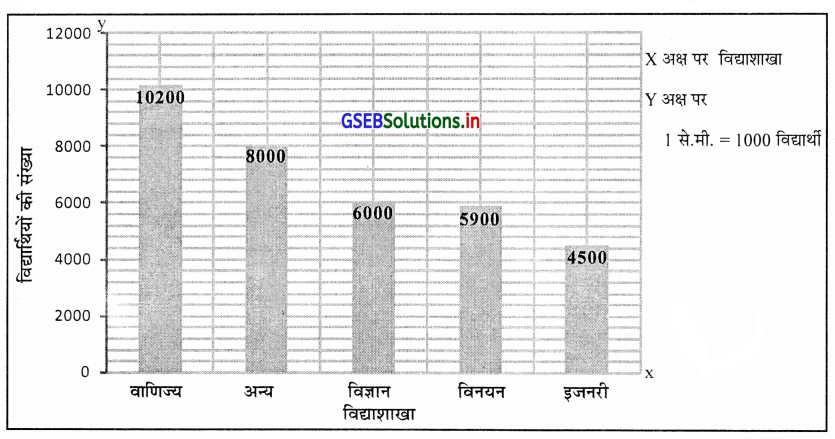
यहा X अक्ष पर विद्याशाखा और Y अक्ष पर योग्य प्रमाणमाप लेकर विद्यार्थीयों की संख्या दर्शायेंगे ।
भिन्न भिन्न विद्याशाखा में विद्याथियों की संख्या प्रस्तुत करनेवाला दण्डचित्र सूचना को उतरते क्रम में गठन करेंगे। प्रथम वाणिज्य विद्याशाखा का दण्डचित्र, दूसरा अन्य, तीसरा विज्ञान, चौथा विनयन और पाचवा इजनेरी विद्याशाखा का दण्डचित्र बनेंगा ।
विभाग – D
निम्न प्रश्नों के उत्तर दीजिए ।
प्रश्न 1.
सांख्यिकी के अभ्यास में वर्गीकरण की आवश्यकता क्यों है ?
उत्तर :
सांख्यिकी के अभ्यास में वर्गीकरण की आवश्यकता निम्न कारणों से है :
- विस्तृत सूचना को संक्षिप्त में, सरलता और आकर्षक प्रस्तुतीकरण करने के लिए ।
- सूचना में भिन्न भिन्न लक्षणों के बीच सरलता से तुलना करने के लिए ।
- अवर्गीकृत सूचना पर से पृथक्करण करने में समय, शक्ति और खर्च अधिक होता है । समय, शक्ति और खर्च की बचत के लिए वर्गीकरण किया जाता है ।
- अभ्यास क्षेत्र के भिन्न भिन्न लक्षणों की सरलता से सूचना प्राप्त कर सकते है ।
![]()
प्रश्न 2.
संख्यात्मक सूचना का वर्गीकरण उचित उदाहरण सहित समझाईए ।
उत्तर :
मानाकि एक किताब में भूलों की संख्या के लिए 100 पन्नों का न्यादर्श पसंद करके किताब में भूलों की संख्या के लिए
सूचना एकत्र किया जाय तो किताब में भूलों की संख्या दर्शाते 100 भिन्न भिन्न अवलोकन प्राप्त होंगे जिसे अवर्गीकृत सूचना कहते है । अब सूचना का अध्ययन करने पर निष्कर्ष प्राप्त हुआ जिसमें एक भी भूल न हो ऐसे 10 पन्ने, एक भूल हो ऐसे 30 पन्ने, दो भूल हो। ऐसे 45 पन्ने और तीन भूल हो ऐसे 15 पन्ने है । उसे संख्यात्मक सूचना का वर्गीकरण कहते है । उसे संक्षिप्त में निम्नानुसार प्रस्तुत करेंगे ।

उपर्युक्त उदाहरण में ‘किताब में भूलों की संख्या’ यह संख्यात्मक चल है इसलिए ऐसे वर्गीकरण को संख्यात्मक सूचना का वर्गीकरण कहते है।
प्रश्न 3.
गुणात्मक सूचना का वर्गीकरण उचित उदाहरण सहित समझाइए ।
उत्तर :
गुणात्मक सूचना के अवलोकनों का वर्गीकरण के लिए स्तर निर्धारित करने के उन्हें पंक्तियों (Rows) स्तंभों (Vertical) में व्यवस्थित
रूप से गठित करने की क्रिया को सारणीयन कहते हैं । गुणात्मक सूचना का वर्गीकरण के दो प्रकार है : (1) सरल सारणी (2) बहुविध सारणी
एक लक्षण का उपयोग किया जाए तो उसे सरल सारणी कहते है । एक गुणधर्म वैवाहिक स्तर अनुसार सरल सारणी का उदाहरण निम्निलिखित है :
| वैवाहित स्तर | व्यक्तियों की संख्या |
| विवाहित | 1500 |
| अविवाहित | 500 |
| कुल | 2000 |
दो या उस से अधिक लक्षणों का उपयोग किया जाए तो उसे बहुविध सारणी कहते है । लड़कों का लिंग, परिणाम के अनुसार बहुविध सारणी का उदाहरण
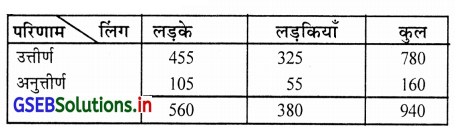
प्रश्न 4.
संचयी आवृत्ति वितरण पर संक्षिप्त टिप्पणी लिखिए।
उत्तर :
चल की किंमत और वर्ग की आवृत्ति और उससे आगे के सभी मूल्यों की वर्गों के आवृत्तियों के योग को संचयी आवृत्ति (cf) कहते हैं और उसके वितरण को संचयी आवृत्ति वितरण कहते हैं।
संक्षेप में आवृत्ति वितरण के कोई भी वर्ग की संचयी आवृत्ति अर्थात् ऊपर के वर्गों की आवृत्तियों का योग असतत आवृत्ति वितरण पर से असतत (खंडित) संचयी आवृत्ति वितरण और अखंडित आवृत्ति वितरण पर से अखंडित संचयी आवृत्ति वितरण प्राप्त कर सकते है। इस प्रकार के संचयी आवृत्ति वितरण को ‘से कम’ प्रकार का संचयी आवृत्ति वितरण (Less than Cumulative Frequency) कहते है। इसी प्रकार चल की निश्चित से अधिक किंमत रखनेवाले अवलोकनों की संख्या को “से अधिक” प्रकार का संचयी आवृत्ति (More than Cumulative Frequency) कहते है । सतत (अखंडित) चर का कोई भी वर्ग का अधःसीमा बिन्दु से अधिक किंमत रखनेवाले कुल अवलोकनों को ‘से अधिक’ प्रकार की संचयी आवृत्ति कहते है ।
प्रश्न 5.
सतत आवृत्ति वितरण (अखंडित) की रचना के मुद्दों की चर्चा करो ।
उत्तर :
अवर्गीकृत सूचना पर से सतत (अखंडित) आवृत्ति वितरण की रचना करते समय ध्यान में रखने योग्य मुद्दे निम्नलिखित है :
(1) सामान्य रूप से वर्गों की संख्या कम से कम 6 और अधिक से अधिक 15 रखनी चाहिए परंतु विशिष्ट परिस्थितियों में सूचना के आधार से 6 से कम या 15 से अधिक वर्गों की संख्या भी ली जाती है ।
(2) वर्गों की संख्या को K से दर्शायेंगे ।
(3) विस्तार R प्राप्त किया जाता है । विस्तार R = महत्तम अवलोकन – लघुतम अवलोकन
(4) दिए गए अवर्गीकृत सूचना के विस्तार को वर्गों की संख्या से भाग देने पर पूर्णांक संख्या जितनी वर्गलंबाई लेनी चाहिए।
c = \(\frac{\mathrm{R}}{\mathrm{K}}\) जहाँ C.K ≥ R
(5) अवर्गीकृत सूचना का लघुत्तम अवलोकन की किमत का समाविष्ट हो उसी तरह प्रथम वर्ग की वर्ग सीमाओं प्राप्त करो _और उसके बाद वर्ग लंबाई के आधार से शेष वर्गों की वर्गसीमाओं प्राप्त करो। अंतिम वर्ग की सीमाओं महत्तम अवलोकन का समावेश हो उसी तरह बनाया जाता है । सामान्यतः वर्ग में वर्गलंबाई समान रखी जाती है। लेकिन सूचना का विस्तार बड़ा हो तब असमान वर्गलंबाई रखी जाती है।
(6) जब आवृत्ति वितरण के वर्ग की मध्यकिंमत और वर्गलंबाई दी गई हो तब वर्ग सीमाबिंदु निम्न सूत्र से प्राप्त किया जाता है ।
वर्गलंबाई वर्ग का अधः सीमाबिंदु = मध्यकिंमत – 
वर्गलंबाई वर्ग का उर्ध्व सीमाबिंदु = मध्यकिंमत + 
(7) सतत सूचना के लिए सामान्यतः निवारक वर्गों की रचना की जाती है । जब असतत सूचना का विस्तार विशाल हो तब अनिवारक वर्गों की रचना करने की प्रणाली है ।
(8) अनिवारक सतत आवृत्ति वितरण पर से संचयी आवृत्ति वितरण की रचना करते समय अनिवारक वर्गों को निवारक वर्गों में परिवर्तित किया जाता है ।
(9) दी गई सतत (अखंडित) आवृत्ति वितरण पर से ‘से कम’ प्रकार का संचयी आवृत्ति प्राप्त करने के लिए प्रथम वर्ग की अधः सीमाबिंदु को उसके पहले के वर्ग उर्ध्व सीमाबिंदु के रूप में लेकर आवृत्ति शून्य दर्शाई जाती है, जबकि ‘से अधिक’ प्रकार के संचयी आवृत्ति में अंतिम वर्ग की उर्ध्व सीमाबिंदु को उसके बाद के वर्ग की अधः सीमाबिंदु के रूप में लेकर उसकी आवृत्ति शून्य दर्शाई जाती है ।
प्रश्न 6.
सारणीयन (कोष्टक) अर्थात् क्या ? उसके उपयोग लिखिए ।
उत्तर :
सूचना के अवलोकनों को वर्गीकरण हेतु निर्देशित स्तरानुसार वर्गीकृत करके उन्हें स्तंभों (Vertical) और पंक्तियों (Rows) में व्यवस्थित रूप से गठित करने की क्रिया को सारणीयन कहते है ।
सारणीयन के उपयोग निम्नलिखित है । (Use of Tabulation) :
- सारणी द्वारा विस्तृत सूचना को संक्षिप्त में, व्यवस्थित रूप से, सरलता व सघनता से प्रस्तुत किया जाता है ।
- समय, शक्ति और धन की बचत होती है ।
- सूचनाओं की तुलना करनी हो तो उन्हें पास पास रखने से तुलना – कार्य सरल बनता है।
- सारणी में स्तंभ – पंक्ति का योग करना होता है । इसलिए यदि कभी भूल से भूल रह गई हो तो उसे ज्ञात करके भूल का सुधार किया जा सकता है ।
- सारणी की सहायता से विश्लेषण, अर्थघटन, निष्कर्ष का कार्य सरल बनता है ।
- सारणीयन से अनावश्यक सूचना को हटाया जा सकता है ।
- सारणीयन द्वारा सूचना को सरलता से लम्बे समय तक याद रख सकते है ।
प्रश्न 7.
सारणी (कोष्टक) (Rule of Tabulation) रचना के मार्गदर्शक सिद्धांतों को समझाइए ।
उत्तर :
सारणी पर से दी गई सूचनाओं का अधिक अर्थपूर्ण रीति से प्रस्तुत करके आवश्यक निर्णय सरलता से विश्लेषण किया जा सके इसलिए कुछ सामान्य नियम निम्नानुसार है :
- सारणी का शीर्षक अध्ययन के अनुकूल होना चाहिए ।
- सारणी में आनेवाला स्तंभ और पंक्ति का शीर्षक स्पष्ट और सरल होना चाहिए ।
- यदि संख्याएँ वड़ी हो तो उसे सो, हजार, लाख या करोड़ में लिखना चाहिए ।
- तुलना करने के लिए संबंधित सूचना का कोलम पास-पास रखना चाहिए ।
- मख्य विभागों तथा उपविभागों की संख्या आवश्यकतानुसार लेनी चाहिए ।
- मुख्य गुणधर्मों अलग दर्शाने के लिए योग्य रेखांकन करना चाहिए ।
- मुख्य और गौण गुणधर्मों को दर्शाते हुए कोलम में योग का कोलम रखना चाहिए ।
- सारणी के अंत में सूचना का स्रोत का उल्लेख करना चाहिए ।
- पक्की सारणी तैयार करने से पूर्व कच्ची सारणी तैयार करना अनुकूल रहता है ।
- सारणी की रचना पश्चात् एक बार उसकी उलट जाच कर लेना चाहिए ।
- प्रत्येक सारणी के खाने के शीर्षक पर सूचना की इकाईयों का निर्देश करना चाहिए ।
- एक ही सारणी में अनेक प्रकार की जानकारी को समाविष्ट नहीं करना चाहिए । यदि आवश्यक हो तो अधिक जानकारी के लिए अलग अलग सारणी बनाना चाहिए ।
![]()
प्रश्न 8.
निम्न आवृत्ति वितरण पर से मूल आवृत्ति वितरण तैयार करो :

उत्तर :
यहाँ मध्यकिंमत के बीच अंतर समान है इसलिए प्रत्येक वर्ग की वर्गलंबाई 100 प्राप्त होगा। अब मध्यकिंमत और वर्ग लंबाई . का उपयोग करके सीमा ज्ञात करेंगे ।
प्रथम वर्ग की अधःसीमा बिंदु = मध्यकिंमत –  = 250 – \(\frac{100}{2}\) = 250 – 50 = 200
= 250 – \(\frac{100}{2}\) = 250 – 50 = 200
प्रथम वर्ग की उर्ध्वसीमा बिंदु = मध्यकिंमत +  = 250 + \(\frac{100}{2}\) = 250 + 50 = 300
= 250 + \(\frac{100}{2}\) = 250 + 50 = 300
∴ प्रथम वर्ग 200 – 300 प्राप्त होगा । उस पर से शेष वर्ग प्राप्त करने के लिए वर्गलंबाई 100 जोड़कर प्राप्त करेंगे ।

प्रश्न 9.
एक ओफिस में कार्यरत 40 कर्मचारियों में 60% स्त्रियाँ थी और शेष 40% पुरुष थे । 50% पुरुष विवाहित थे जब कि विवाहित और अविवाहित स्त्रियों का अनुपात 5:3 था । उपर्युक्त सूचना को योग्य सारणी में प्रस्तुत करो ।
उत्तर :
यहाँ दो गुणधर्म (1) लिंग : पुरुष, स्त्री ( 2 ) वैवाहित स्तर : विवाहित, अविवाहित
कल कर्मचारी 40 के 60% स्त्रियाँ \(\frac{40 \times 60}{100}\) = 24 स्त्रियाँ और 40% पुरुष \(\frac{40 \times 40}{100}\) = 16 पुरुष । 50% पुरुष विवाहित है अर्थात्
16 का 50% = 8 पुरुष विवाहित ∴ अविवाहित पुरुष = 16 – 8 = 8
विवाहित और अविवाहित स्त्रियों का अनुपात 5:3 था ।
∴ विवाहित स्त्रियाँ = \(\frac{24 \times 5}{8}\) = 15 और विवाहित स्त्रियाँ = \(\frac{24 \times 3}{8}\) = 9 उसे सारणी में दर्शायेंगे ।
एक ओफिस में कार्यरत 40 कर्मचारियों का लिंग, विवाहित स्तर के अनुसार सारणी

प्रश्न 10.
100 कर्मचारियों के मासिक आय की निम्न सूचना पर से मूल आवृत्ति वितरण तैयार करो ।

उत्तर :
‘से कम’ प्रकार का आवृत्ति वितरण दिया है। प्रथम वर्ग की संचयी आवृत्ति 0 है, इसलिए प्रथम वर्ग की अधःसीमा 2400 होगी और वर्गलंबाई 500 समान है । उसके लिए मूल आवृत्ति वितरण निम्न प्राप्त होगा ।
| मासिक आय | आवृत्ति (f) |
| 2400 – 2900 | 3 – 0 = 3 |
| 2900 – 3400 | 12 – 3 = 9 |
| 3400 – 3900 | 30 – 12 = 18 |
| 3900 – 4400 | 55 – 30 = 25 |
| 4400 – 4900 | 78 – 55 = 23 |
| 4900 – 5400 | 88 – 78 = 10 |
| 5400 – 5900 | 95 – 88 = 07 |
| 5900 – 6400 | 100 – 95 = 05 |
| कुल | 100 |
प्रश्न 11.
किसी एक परीक्षा में 200 विद्यार्थियों के नंबर की निम्न सूचना पर से मूल आवृत्ति वितरण तैयार करो ।

उत्तर :
यहाँ उर्ध्वसीमा 100 की बनी है, इसलिए से अधिक प्रकार आवृत्ति वितरण है और वर्ग लंबाई समान 10 है, इसलिए प्रथम वर्ग 10-20 और शेष के लिए 10 वर्ग लंबाई लेकर निम्नानुसार मूल आवृत्ति वितरण प्राप्त होगा ।
200 विद्यार्थियों के गुण (नंबर) का निवारक सतत आवृत्ति वितरण
| गुण | आवृत्ति (f) |
| 10 – 20 | 200 – 180 = 20 |
| 20 – 30 | 180 – 140 = 40 |
| 30 – 40 | 140 – 90 = 50 |
| 40 – 50 | 90 – 55 = 35 |
| 50 – 60 | 55 – 30 = 25 |
| 60 – 70 | 30 – 08 = 22 |
| 70 – 80 | 08 – 02 = 06 |
| 80 – 90 | 02 – 01 = 01 |
| 90 – 100 | 1 = 01 |
| कुल | 200 |
प्रश्न 12.
निम्न आवृत्ति वितरण पर से मूल आवृत्ति वितरण तैयार करो ।

उत्तर :
यहा मध्यकिंमत के बीच अंतर समान है इसलिए प्रत्येक वर्ग की वर्गलंबाई 5 होगी। अब वर्गलंबाई और मध्यकिंमत का उपयोग करके समीबिंदु ज्ञात करेंगे ।
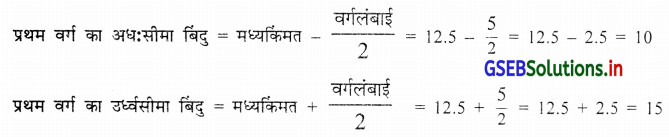
∴ प्रथम वर्ग 10-15 प्राप्त होगा । उस पर से शेष वर्ग प्राप्त करने के लिए वर्गलंबाई 5 जोड़कर प्राप्त करेंगे ।

![]()
प्रश्न 13.
अहमदाबाद शहर में जनसंख्या के परिवहन के लिए कुल 1000 बस है । उसमें से 350 बस BRTS और शेष AMTS के बस के रूप में उपयोग में लिया जाता है । कुल 400 एरकन्डीशन बस में से 250 BRTS बस है, तो उपर्युक्त सूचना को योग्य सारणी में प्रस्तुत करो ।
उत्तर :
अहमदाबाद शहर में जनसंख्या के परिवहन के उपयोग में लीए जानेवाली BRTS, AMTS की बस का प्रकार दर्शाती सारणी
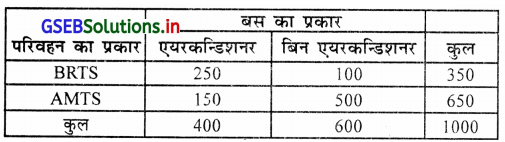
प्रश्न 14.
एक कोलेज के कुल 1500 विद्यार्थियों में से 900 लड़के थे, उसमें से 250 लड़के विज्ञान प्रवाह में थे जबकि 250 लड़कियाँ वाणिज्य प्रवाह में थी । उपर्युक्त सूचना को योग्य सारणी में प्रस्तुत करो ।
उत्तर :
यहाँ दो गुणधर्म
(1) लिंग : लड़के, लड़कियाँ
(2) प्रवाह : विज्ञानप्रवाह, वाणिज्य प्रवाह
एक कोलेज के विद्यार्थियों की लिंग प्रवाह दर्शाती हई सारणी
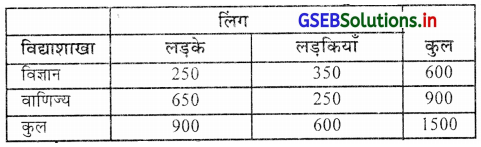
प्रश्न 15.
सांख्यिकी के अभ्यास में आकृति का महत्त्व समझाइए ।
उत्तर :
आकृत्ति का महत्त्व निम्नलिखित है :
- संख्यात्मक सूचनाओं को आकृति द्वारा प्रस्तुत करने से दर्शक को आकर्षक लगता है।
- सूचनाओं की विशेषताओं को दीर्घकाल तक याद रखा जा सकता है ।
- चित्रों द्वारा सूचना को सुगमता से समझाया जा सकता है ।
- दो या अधिक समूह के प्रमाण में आकृतियाँ खींची जाए तो उस पर से सरलता से तुलनात्मक अभ्यास किया जा सकता है।
- आकृति द्वारा प्रस्तुतीकरण करने से अशिक्षित या कम पढ़े-लिखे एवं बालकों की सूचना का हार्द सरलता से समझाया जा सकता है ।
- सूचना को दर्शनीय आकृति द्वारा प्रस्तुत किया हो तो उसके अभ्यास में समय की बचत होती है ।
- उत्पादक और व्यापारी सुयोग्य व आकर्षक ढंग से आकृति का उपयोग करके विज्ञापन का कार्य सरल बनाया जा सकता है ।
- सामाजिक सुधार के अभियान में लोक मानस पर अपेक्षित प्रभाव डालने या उसका विकास करने के लिए चित्र एक प्रभावशाली साधन है।
- आकृति को समझने में भाषा का बंधन नहीं है ।
- समाजशास्त्र, अर्थशास्त्र, मनोविज्ञान जैसे विषयों में कुछ महत्त्व की पुष्टि के लिए, विषय स्पष्टीकरण हेतु चित्रों का सघन उपयोग किया जाता है ।
प्रश्न 16.
एकायामी आकृति पर टिप्पणी लिखिए ।
उत्तर :
जब दी गई सूचना के किसी एक ही परिमाण को लक्ष में लेकर चित्र बनाया जाए तो उस चित्र को एकायामी चित्र कहते है।
एकायामी आकृति में निम्नलिखित आकृति का अध्ययन किया जाता है ।
- दण्डचित्र
- बहुगुणी दण्डचित्र (पास पास के स्तंभ दर्शाती आकृति)
- सरल अन्तर्विभक्त दण्डचित्र (सरल विभाजित दण्डचित्र)
- प्रतिशत अन्तविभक्त दण्डचित्र (प्रतिशत विभाजित दण्डचित्र)
प्रश्न 17.
द्वि-मापी आकृति पर टिप्पणी लिखिए ।
उत्तर :
दी गई सूचना की मात्रा संख्यात्मक रुप से बड़ी या विस्तृत हो तो एकायामी चित्र काम में नहीं आ सकता । इस कठिनाई को दूर करने के लिए द्वि-आयामी आकृति का उपयोग प्रस्तुतीकरण की दृष्टि के अधिक उपयोगी हो सकता है । ऐसे चित्रों में लम्बाई और चौड़ाई दोनों माप ध्यान में लिए जाते है । यहाँ कुल मात्रा को आकृति के क्षेत्रफल जितना गिनकर आकृति को रेखांकित किया जाता है, परिणामस्वरूप इन में वर्गाकार, आयात, वृतांश आकृति का समावेश किया है ।
प्रश्न 18.
चित्राकृति उदाहरण सहित समझाइए।
उत्तर :
इसमें सूचना को तस्वीरो के रूप में प्रस्तुत करते है । इसलिए चित्राकृति कहा जाता है । चित्रों द्वारा सूचना रसप्रद और आकर्षक बनती है । निरक्षर व्यक्ति और बालक को सरलता से चित्राकृति द्वारा समझाया जा सकता है । चित्र लेखक को आइसोटाइप (ISOTYPE) भी कहा जाता है । विश्व में अलग अलग भागों में लिखने-पढ़ने की भाषा अलग अलग है। जिससे किसी एक भाषा में लिखी गई जानकारी उस भाषा को नहीं जाननेवाले व्यक्ति पढ़ नहीं सकते है। यदि उस सूचना को चित्र द्वारा प्रस्तुत किया जाए जैसे कि गाय का चित्र, फल, फूल, दूध की बोतल का चित्र बनाया जाए तो सभी लोग आसानी से समझ सकते है । चित्रों को भाषा के बंधन नहीं होते ।
![]()
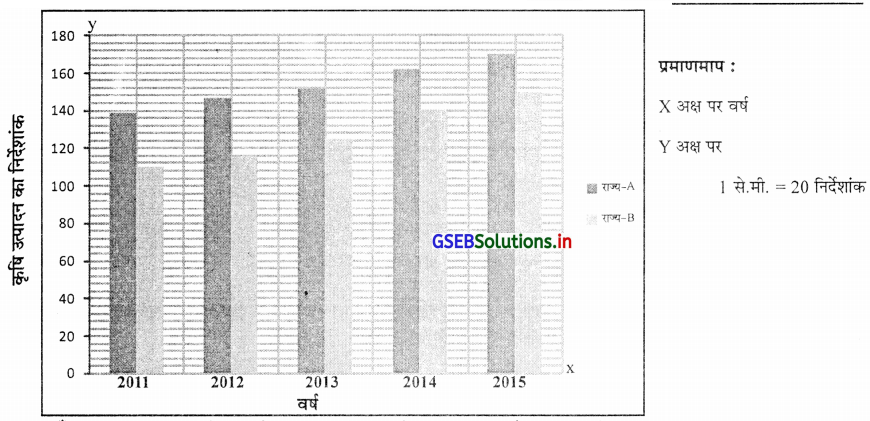
प्रश्न 19.
दो भिन्न भिन्न राज्य के कृषि उत्पादन का निर्देशांक निम्नानुसार है, उसे योग्य आकृति में प्रस्तुत करो ।

उत्तर :
सूचना वर्ष (समय) अनुसार दी गई है इसलिए सूचना उतरते क्रम में गठित नहीं होगी। वर्ष के अनुसार ही दण्ड चित्रों की रचना करेंगे । दो राज्य की सूचना के लिए पासपास की (बहुगुणी) दण्डचित्र की रचना करेंगे । इस के लिए X अक्ष पर वर्ष और Y अक्ष पर योग्य प्रमाणमाप लेकर कृषि उत्पादन दर्शायेंगे ।
प्रश्न 20.
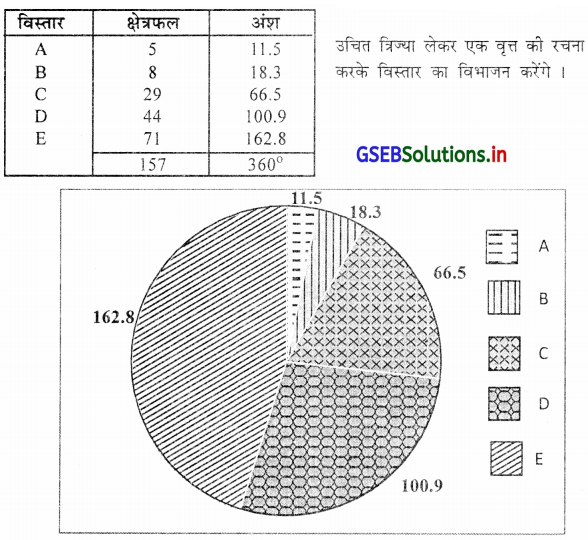
पाँच भिन्न भिन्न विस्तारों का क्षेत्रफल (वर्ग मी. में) निम्नानुसार है, उस पर से वतांश आकति की रचना कीजिए ।

उत्तर :
भिन्न भिन्न विस्तारों के लिए अंश निकाल कर वृत्तांश आकृति की रचना निम्नानुसार करेंगे ।
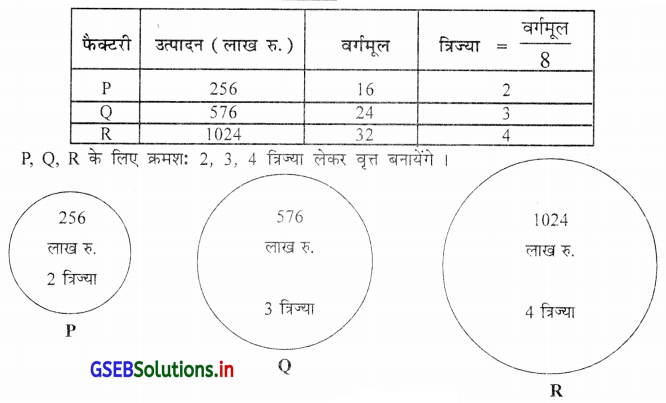
प्रश्न 21.
भिन्न भिन्न फैक्टरी में उत्पादन का विवरण निम्नानुसार है, उसे उचित आकृति में प्रस्तुत करो ।

उत्तर :
सूचना का विस्तार बड़ा है इसलिए वर्गमूल प्राप्त करके उचित त्रिज्या लेकर वृत्त चित्राकृति में प्रस्तुत करेंगे ।
विभाग – E
निम्न के हल प्राप्त कीजिए ।
प्रश्न 1.
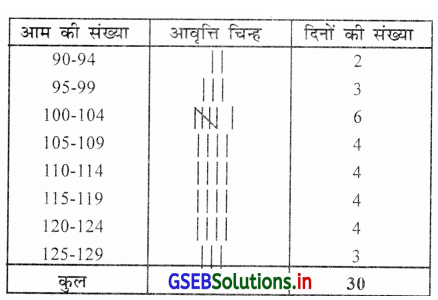
मौसम के दौरान एक आम के खेत में भिन्न भिन्न आम के पेड़ पर 30 दिन के दौरान प्राप्त आम की संख्या निम्नानुसार है, तो वर्गान्तर 5 लेकर आवृत्ति वितरण तैयार करो ।

उत्तर :
आम के पेड़ पर आम की संख्या यह असतत (खंडित) चल है ।
सूचना का विस्तार R = 128 – 92 = 36
सूचना का विस्तार बड़ा है और चल असतत (खंडित) है इसलिए अनिवारक सतत आवृत्ति वितरण तैयार करेंगे ।
आम के खेत में 30 दिन के दौरान आम के पेड़ पर आम का अनिवारक सतत आवृत्ति वितरण
प्रश्न 2.
किसी एक दिन दौरान एक शहर के 40 रिक्षा ड्राइवर द्वारा की गई आमदानी (रु.) में निम्नानुसार है । उस पर से एक वर्ग 220-239 हो ऐसा 20 वर्गलंबाई हो ऐसा आवृत्ति वितरण तैयार करो ।
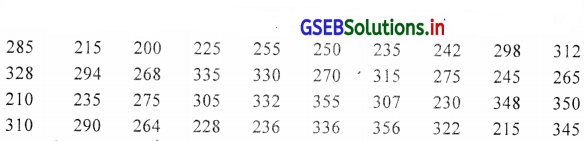
उत्तर :
एक वर्ग 220-239 और वर्गलंबाई 20 हो ऐसा अनिवारक सतत वर्ग प्राप्त करेंगे ।
सूचना का विस्तार R = 356 – 200 = 156
प्रथम वर्ग 200-219 का होगा ।
एक शहर के 40 रिक्षा ड्राईवर की दैनिक आय का अनिवारक सतत आवृत्ति वितरण
![]()
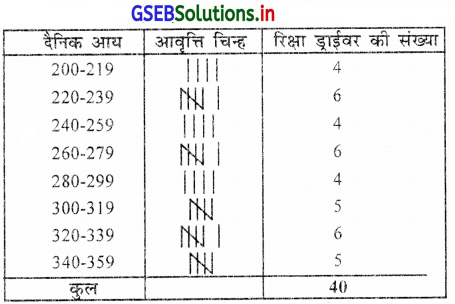
प्रश्न 3.
शहर के एक विस्तार में 50 मकान में एक महिना दौरान पानी उपयोग की इकाई की निम्नानुसार सूचना पर से एक वर्ग 25-30 हो ऐसा निवारक सतत आवृत्ति वितरण तैयार करो ।

उत्तर :
यहाँ सबसे बड़ा अवलोकन = 57 और सबसे छोटा अवलोकन मूल्य = 24 है ।
∴ विस्तार R = 57 – 24 = 33 होगा । एक वर्ग 25-30 हो एसा निवारक वर्ग बनाना है ।
∴ वर्ग 20-25, 25-30 ….. बनेंगे ।
शहर के एक विस्तार में 50 मकान में एक महिना दौरान पानी का उपयोग दर्शाता हुआ निवारक सतत आवृत्ति वितरण
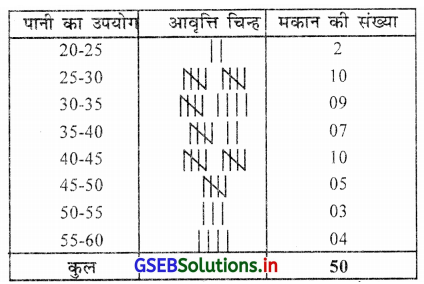
प्रश्न 4.
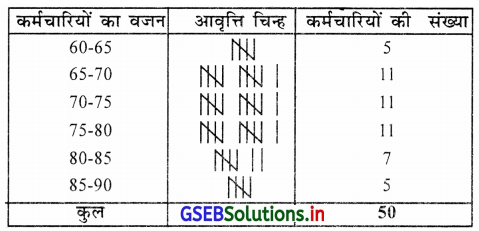
किसी एक कंपनी में कार्यरत 50 कर्मचारियों का वजन (किग्रा) में निम्नानुसार है। अंतिम वर्ग 85-90 हो ऐसा निवारक सतत आवृत्ति वितरण तैयार करो ।
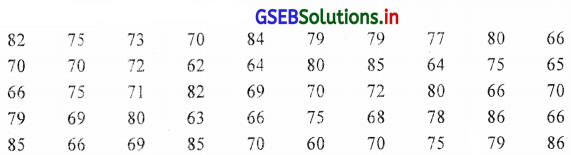
उत्तर :
यहाँ अंतिम वर्ग 85-90 का दिया है।
∴ वर्गलंबाई 5 लेकर अनिवारक वर्ग प्राप्त करेंगे महत्तम अवलोकन = 86, न्यूनतम अवलोकन = 60
∴ विस्तार R = 86 – 60 = 26
50 कर्मचारियों का वजन (किग्रा.) में दर्शाता हुआ निवारक सतत आवृत्ति वितरण
प्रश्न 5.
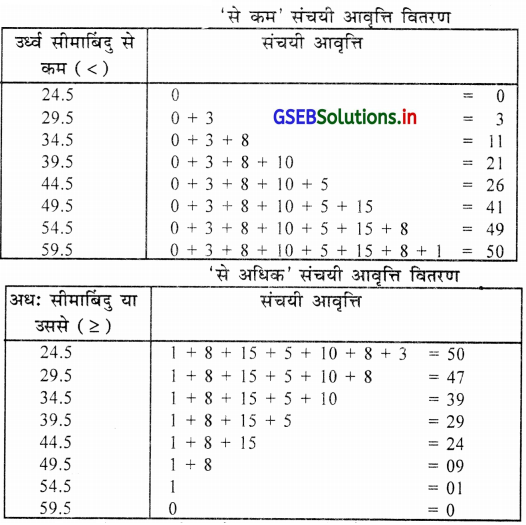
निम्न आवृत्ति वितरण पर से ‘से कम’ और ‘से अधिक’ प्रकार का संचयी आवृत्ति वितरण ज्ञात करो ।

उत्तर :
उपयुक्त आवृत्ति वितरण अनिवारक (Inclusive) होने से सर्व प्रथम अधःसीमाबिन्दु और उर्ध्वसीमा बिन्दु ज्ञात करके पुनः आवृत्ति
वितरण लिखेंगे । और उस पर से ‘से कम’ और ‘से अधिक’ प्रकार का आवृत्ति वितरण प्राप्त करेंगे । अधःसीमा में से 0.5 घटाकर और उर्ध्वसीमा में 0.5 जोड़कर निम्नानुसार वर्ग प्राप्त करेंगे ।
| वर्ग | आवृत्ति |
| 24.5 – 29.5 | 3 |
| 29.5 – 34.5 | 8 |
| 34.5 – 39.5 | 10 |
| 39.5 – 44.5 | 5 |
| 44.5 – 49.5 | 15 |
| 49.5 – 54.5 | 8 |
| 54.5 – 59.5 | 1 |
| कुल | 50 |
प्रश्न 6.
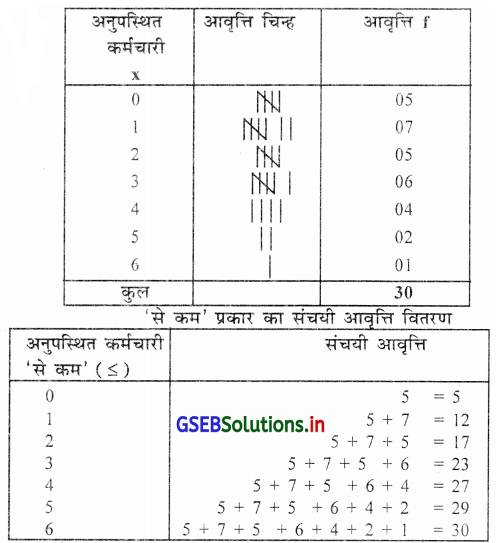
एक कारखाना में कार्यरत 30 कर्मचारियों की 30 दिन के दौरान अनुपस्थिति की संख्या निम्नानुसार है, तो उचित आवृत्ति
वितरण तैयार करो । उस पर से ‘से कम’ प्रकार का संचयी आवृत्ति वितरण तैयार करो ।

उत्तर :
महत्तम अवलोकन = 6 और लघुतम अवलोकन = 0 है । सूचना असतत (खंडित) है । इसलिए निम्नानुसार असतत आवृत्ति वितरण प्राप्त करेंगे।
कारखाना में 30 दिन दौरान अनुपस्थित कर्मचारियों की संख्या प्रदर्शित करती असतत (खंडित ) आवृत्ति वितरण
प्रश्न 7.
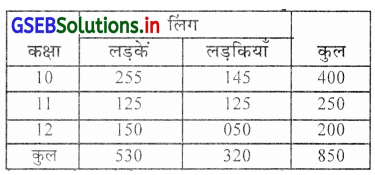
एक विद्यालय में कुल 850 विद्यार्थी थे । जिसमें कक्षा 10, 11, 12 में विद्यार्थियों का अनुपात 8 : 5 : 4 था । कक्षा 10वीं में विद्यालय में कल विद्यार्थियों के 30% लड़के थे । कक्षा 11 वीं में लड़के और लड़कियों की संख्या समान थी। जब कि कक्षा 12वीं में लड़कों की संख्या लड़कियों की अपेक्षा तीन गुना थी । उपर्युक्त सूचना को सारणी में प्रस्तुत करो ।
उत्तर :
कुल विद्यार्थी 850 है । कक्षा 10, 11, 12 में विद्यार्थियों का अनुपात 8 : 5 : 4 था ।
∴ कक्षा 10वी में विद्यार्थियों की संख्या = \(\frac{850 \times 8}{17}\) = 400
∴ कक्षा 11वी में विद्यार्थियों की संख्या = \(\frac{850 \times 5}{17}\) = 250
∴ कक्षा 12वी में विद्यार्थियों की संख्या = \(\frac{850 \times 4}{17}\) = 200
10वीं में लड़कों की संख्या 30% है, ∴ 10वी में लड़के = \(\frac{850 \times 30}{100}\) = 255
कक्षा 11 वीमें लड़के और लड़कियाँ समान थी अर्थात् 125 लड़के और 125 लड़कियाँ होंगी ।
कक्षा 12वी में लड़के और लड़कियाँ का अनुपात 3 : 1 बनेगा ।
∴ लड़कों की संख्या = \(\frac{200 \times 3}{4}\) = 150 और लडकियाँ \(\frac{200 \times 1}{4}\) = 50
उपर्युक्त सूचना को निम्न सारणी में प्रस्तुत करेंगे ।
विद्यालय के 850 विद्यार्थियों का कक्षा, लिंग के अनुसार सारणी
![]()
प्रश्न 8.
एक विद्यालय में 2013 के वर्ष में कुल 1200 विद्यार्थी अभ्यास करते थे । उसमें कुल 400 लड़कियाँ थी और उसमें से 50 लड़कियाँ होस्टेल में नहीं रहती थी । विद्यालय के कुल 600 लड़के होस्टेल में रहते थे । 2014 के वर्ष में विद्यालय में लड़कों की संख्या में 20% और लड़कियों की संख्या में 30% (प्रतिशत) की वृद्धि हुई । उसी वर्ष 260 लड़कें और 100 लड़कियाँ होस्टेल में रहते नहीं थे । वर्ष 2015 में विद्यालय में 140 लड़के और 100 लड़कियों की वृद्धि हुई और वह सभी होस्टेल में रहते थे । उपर्युक्त सूचना को योग्य सारणी में प्रस्तुत करो ।
उत्तर :
यहाँ तीन गुणधर्म :
(1) वर्ष : 2013, 2014, 2015
(2) लिंग : लड़के, लड़कियाँ
(3) होस्टेल का निवासी : निवासी, बिननिवासी
तीनों गुणधर्म का उपयोग करके निम्नानुसार सारणी में प्रस्तुत करेंगे ।
वर्ष 2013 से 2015 के दौरान विद्यार्थियों की लिंग के अनुसार होस्टेल रहनेवाले और नहि रहनेवाले विद्यार्थियों दर्शाती सारंणी
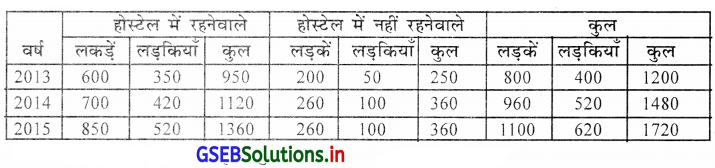
नोंध : वर्ष 2014 में 20% वृद्धि हुई ∴ 800 के 20%
लडकें \(\frac{800 \times 20}{100}\) = 160 की वृद्धि कुल लड़के = 800 + 160 = 960
लड़कियों की संख्या में 30% वृद्धि अर्थात् \(\frac{400 \times 30}{100}\) = 120
∴ कुल लड़कियाँ 400 + 120 = 520
प्रश्न 9.
निम्न सूचना को उचित सारणी में प्रस्तुत करो ।
किसी एक बैंक में नौकरी के विज्ञापन के प्रत्युतर में कुल 2000 आवेदन मिलें, उस में से 50 प्रतिशत उम्मीदवार स्नातक थे, 40% उम्मीदवार अनुस्नातक थे। जबकि 10 प्रतिशत उम्मीदवार अन्य व्यावसायिक योग्यता प्राप्त थे । स्नातक उम्मीदवारों में से 60 प्रतिशत पुरुष थे और उसमें से 25 प्रतिशत विवाहित थे, 40 प्रतिशत स्नातक स्त्री उम्मीदवार विवाहित थी । अनुस्नातक उम्मीदवारों में से 60 प्रतिशत पुरुष थे । उसमें से 40 प्रतिशत विवाहित थे जबकि अनुस्नातक स्त्रियों में से 50 प्रतिशत स्त्रियाँ विवाहित थी । व्यावसायिक योग्यतावाली 30 प्रतिशत स्त्रियों में से 60 प्रतिशत स्त्रियाँ विवाहित थी। जबकि उस में विवाहित और अविवाहित पुरुषों की संख्या समान थी ।
उत्तर :
कुल 2000 आवेदन प्राप्त हुए है । उसमें से स्नातक उम्मीदवार \(\frac{2000 \times 50}{100}\) = 1000 स्नातक
अनुस्नातक उम्मीदवार = \(\frac{2000 \times 40}{100}\) = 800
अन्य व्यावसायिक योग्यतावाले \(\frac{2000 \times 10}{100}\) = 200
स्नातक उम्मीदवारों के 60% पुरुष थे, अर्थात् \(\frac{1000 \times 60}{100}\) = 600
∴ पुरुष स्नातक = 600
∴ स्त्री स्नातक = 400 (1000 – 600 पुरुष)
विवाहित स्नातक पुरुष = \(\frac{600 \times 25}{100}\) = 150
∴ अविवाहित स्नातक पुरुष = 600 – 150 = 450
⇒ विवाहित स्नातक स्त्रियाँ = \(\frac{400 \times 40}{100}\) = 160
∴ अविवाहित स्नातक स्त्रियाँ = 400 – 160 = 240
अनुस्नातक कुल उम्मीदवार 800 में 60% पुरुष अर्थात् का \(\frac{800 \times 60}{100}\) = 480 पुरुष थे ।
∴ अनुस्नातक स्त्रियाँ = 800 – 480 = 320
अनुस्नातक विवाहित पुरुष = \(\frac{480 \times 40}{100}\) = 192
अनुस्नातक अविवाहित पुरुष = 480 – 192 = 288
∴ अनुस्नातक विवाहित स्त्रियाँ = \(\frac{320 \times 50}{100}\) = 160
अनुस्नातक अविवाहित स्त्रियाँ = 320 – 160 = 160
व्यावसायिक योग्यतावाली स्त्रियाँ = \(\frac{200 \times 30}{100}\) = 60
∴ व्यावसायिक विवाहित स्त्रियाँ = \(\frac{60 \times 60}{100}\) = 36
∴ व्यावसायिक अविवाहित स्त्रियाँ = 60 – 36 = 24
∴ व्यावसायिक पुरुष = 200 – 60 = 140
∴ विवाहित व्यावसायिक पुरुष = 70
∴ अविवाहित व्यावसायिक पुरुष = 70
∴ उपर्युक्त सूचना को सारणी में प्रस्तुत करने पर
एक बैंक में 2000 उम्मीदवारों के आवेदन का अभ्यास, लिंग, वैवाहित स्तर के अनुसार सारणी
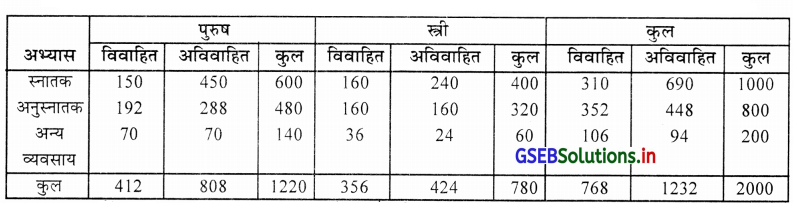
प्रश्न 10.
एक कारखाना में कार्यरत कर्मचारियों का वर्ष, लिंग और निवासस्थान अनुसार संख्या दर्शाती सारणी निम्नानुसार है ।

उपर्युक्त सारणी से आधारित निम्नलिखित प्रश्नों के उत्तर दीजिए ।
(1) 5 वर्ष के काल में कारीगरों की कुल संख्या में कितने प्रतिशत वृद्धि हुई ?
(2) वर्ष 2015 के वर्ष में अस्थानिक कारीगरों की संख्या में कितने प्रतिशत की कमी आई ?
(3) 5 वर्ष के समय काल में पुरुष तथा स्त्रियों की संख्या में कितने प्रतिशत वृद्धि हुई ?
उत्तर :
(1) 5 वर्ष के काल में कारीगरों की कुल संख्या में वृद्धि = 3000 – 2000 = 1000
∴ प्रतिशत = \(\frac{1000 \times 100}{200}\) = 50%
इसलिए 5 वर्ष के काल में कारीगरों की संख्या में 50% वृद्धि हुई है ।
(2) वर्ष 2015 के वर्ष में अस्थानिक कारीगरों की संख्या में कमी = 500 – 400 = 100
∴ प्रतिशत कमी = \(\frac{100 \times 100}{500}\) = 20%
इसलिए वर्ष 2015 के वर्ष में अस्थानिक कारीगरों की संख्या में 20% कमी हुई है ।
(3) 5 वर्ष में समय काल में पुरुषों की संख्या में हुई वृद्धि = 2300 – 1500 = 800
∴ प्रतिशत वृद्धि = \(\frac{800 \times 100}{1500}\) = 53.33%
स्त्रियों की संख्या में वृद्धि = 700 – 500 = 200
∴ प्रतिशत वद्धि = \(\frac{200 \times 100}{500}\) = 40%
इसलिए 5 वर्ष के समय-काल मे पुरुषों की संख्या में 53.33% वृद्धि और स्त्रियों की संख्या में 40% की वृद्धि हुई है।
प्रश्न 11.
एक मोबाइल कंपनी दो प्रकार के मोबाइल का उत्पादन और बिक्री करती है। उसकी निम्न सूचना पर से उचित आकृति में प्रस्तुत कीजिए।
| विवरण | मोबाइल A | मोबाइल B |
| कच्चा माल का खर्च | 5000 | 6000 |
| स्पेरपार्ट जोड़ने का खर्च | 3000 | 3000 |
| अन्य खर्च | 4000 | 4500 |
| कुल खर्च | 12000 | 13500 |
| बिक्री मूल्य | 13,000 | 15,000 |
उत्तर :
मोबाइल A तथा मोबाइल B की सूचना पर से सरल अन्तविभक्त (सरल विभाजित) दण्डचित्र में प्रस्तुत करेंगे । इसके लिए दोनों के लाभ को ध्यान में लेंगे । मोबाइल A में 13000 – 12000 = 1000 लाभ प्राप्त होता है । मोबाईल B में 15,000 – 13,500 = 1,500 का लाभ प्राप्त होता है । मोबाइल A में 13000 बिक्रीमूल्य है।
∴ 1 सेमी = 1000 लेकर 13 सेमी ऊँचाई का स्तंभ बनाकर विभाजन करेंगे, उसी प्रकार मोबाइल B में 15000 बिक्रीमल्य है ।
∴ 1 सेमी = 1000 लेकर 15 सेमी ऊँचाई का स्तंभ बनाकर विभाजन करेंगे,
X अक्ष पर मोबाइल A और B Y अक्ष पर 1 सेमी = 1000 बिक्री
विवरण का विभाजन करनेवाली रेखा की गणना निम्नानुसार करके आलेख में दर्शायेंगे ।
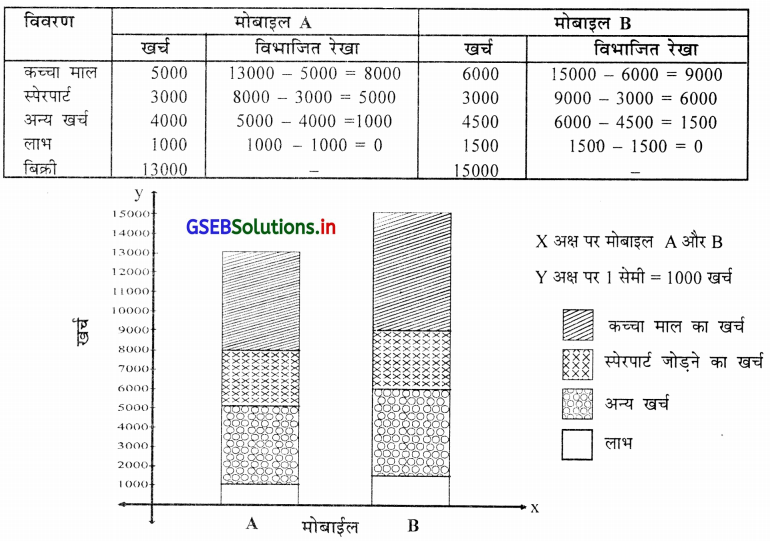
![]()
प्रश्न 12.
दो परिवारों के मासिक खर्च का विवरण निम्नलिखित है । उसे वृत्तांश-आकृति द्वारा प्रस्तुत कीजिए ।
| विवरण | परिवार – A | परिवार – B |
| भोजन | 20000 | 16000 |
| ईधन | 5000 | 4000 |
| परिवहन | 10000 | 8800 |
| मकान भाड़ा | 15000 | 18000 |
| अन्य | 22000 | 18000 |
उत्तर :
वृत्तांश आकृति के लिए परिवार A और परिवार B के खर्च का विवरण के अनुरूप ज्ञात करेंगे ।
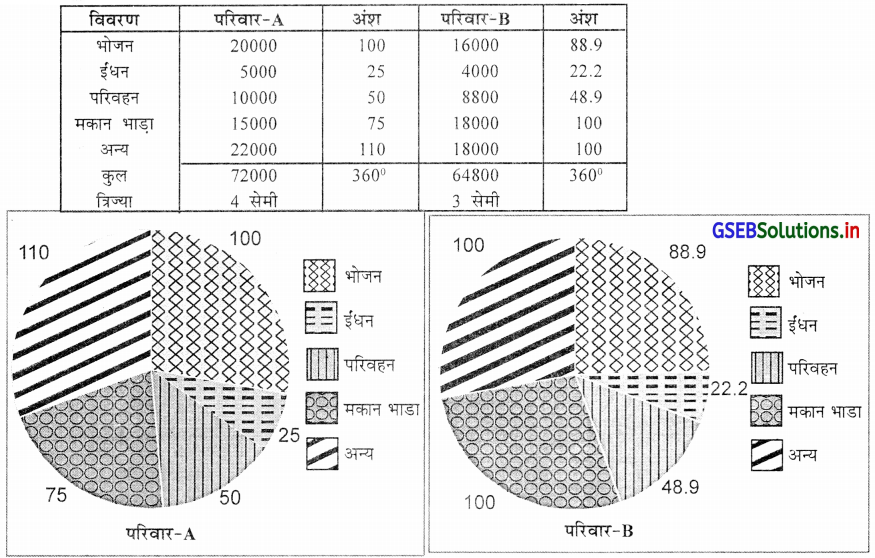
विभाग – F
निम्न प्रश्नों के हल प्राप्त करो ।
प्रश्न 1.
आँख के लिए लेन्स बनानेवाली एक इकाई में एक दिन के दौरान उत्पादन हुए थोक में से 25 लेन्स का एक निदर्श में
लेन्स की मोटाई मि.मि. में निम्नानुसार प्राप्त हुई है । उस पर से समान वर्गलंबाईवाले पाँच वर्गों में विभाजित करो ।

यदि उत्पादन इकाई के अधिकारी ऐसा निश्चित करें कि 1.510 मि.मि. से कम और 1.525 मि.मि. या उससे अधिक मोटाईवाले लेन्स को दोषयुक्त माना जाए तो उस परसे आपने किये वर्गीकरण में कितने प्रतिशत इकाईयाँ दोषयुक्त होगी वह बताइए ।
उत्तर :
यहाँ महत्तम अवलोकन = 1.528 और लघुत्तम अवलोकन = 1.505
∴ विस्तार R = 1.528 – 1.505 = 0.023
वर्गों की संख्या K = 5 दिए गए है ।
∴ वर्गलंबाई = \(\frac{\mathrm{R}}{\mathrm{K}}\) = \(\frac{0.023}{5}\) = 0.0046
नजदिक के पूर्णांक 0.005 वर्गलंबाई (c) रखेंगे ।
आँखों के लेन्स की मोटाई दर्शाता हआ निवारक सतत आवृत्ति वितरण
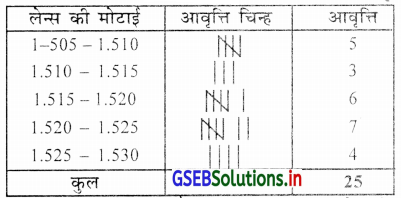
अब 1.510 मि.मि. से कम और 1.525 मिमि या उससे अधिक मोटाईवाले लेन्स को दोषयुक्त मानना है ।
∴ 1.510 मिमि से कम = 05 लेन्स
∴ 1.525 मिमि से अधिक = 04 लेन्स
कुल = 09 लेन्स
कुल 25 लेन्स में से 09 लेख दोषयुक्त होंगे
∴ दोषयुक्त लेन्स के प्रतिशत = \(\frac{100 \times 9}{25}\) = 36%
दोषयुक्त लेन्स की प्रतिशतता = 36 होगी ।
प्रश्न 2.
शेयर बाजार में एक शेयर के मूल्य 30 दिन के दौरान निम्न थे । उस पर से एक वर्ग की वर्गसीमा 18.5 – 20.5 हो ऐसा निवारक सतत (अखंडित) आवृत्ति वितरण तैयार करो ।

निम्न प्रश्नों के उत्तर दीजिए ।
(1) चौथे वर्ग की मध्यकिंमत लिखो ।
(2) शेयर का बंधमूल्य अधिक से अधिक रु. 16.50 हो ऐसे दिन की संख्या कितनी ?
(3) शेयर का बंध मूल्य कम से कम रु. 19.50 हो ऐसे दिन की संख्या कितनी ?
उत्तर :
एक वर्ग 18.5 – 20.5 दिया है इसलिए वर्गलंबाई 2 लेकर निवारक सतत (अखंडित) आवृत्ति वितरण तैयार करेंगे । महत्तम अवलोकन = 20.80 और न्यूनतम अवलोकन = 10.50 का समावेश के लिए प्रथम वर्ग 10.50 – 12.50 और अंतिम वर्ग 20.50 – 22.50 का रखेंगे ।
30 दिन दौरान शेयर का बंधमूल्य में परिवर्तन प्रस्तुत करता निवारक सतत आवृत्ति वितरण
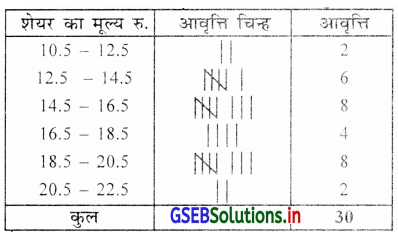
(1) चौथे वर्ग की मध्यकिंमत :

(2) शेयर का बंध मूल्य अधिक से अधिक रु. 16.50 हो ऐसे दिन की संख्या = 2 + 6 + 8 = 16 दिन
(3) शेयर का बंध मूल्य कम से कम रु. 19.50 हो ऐसे दिन की संख्या
18.50 – 20.5 में आवृत्ति 8 है ।
∴ 19.50 से अधिक (19.50 – 20.5 में 4) 4 + 20.5-22.5 के वर्ग की आवृत्ति 2 है ।
∴ 19.50 से अधिक दिन की संख्या = 4 + 2 = 6 दिन
![]()
प्रश्न 3.
एक कारखाना के मालिक द्वारा प्रतिदिन गृहउपयोग में उपयोगी हो ऐसा 50 मिक्क्षर का उत्पादन करने का निश्चित किया था, लेकिन कारीगरों की संख्या में परिवर्तन होने से प्रतिदिन भिन्न भिन्न संख्या में मिक्क्षर का उत्पादन होता था । 40 दिन के दौरान उत्पादन में परिवर्तन निश्चित संख्या 100 के सापेक्ष में निम्नानुसार दर्ज किया गया । उस पर से किसी एक वर्ग की मध्यकिंमत 3 और वर्गलंबाई 6 हो ऐसा निवारक सतत आवृत्ति वितरण तैयार कीजिए ।
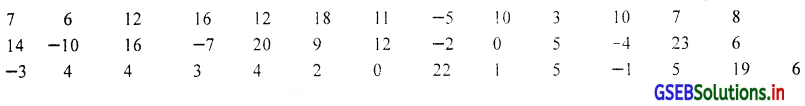
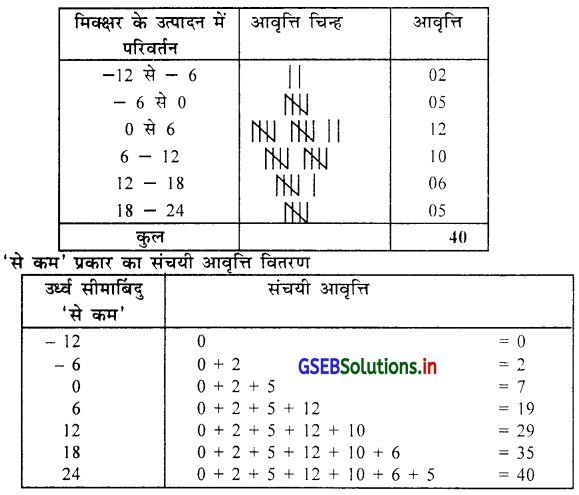
उस पर से ‘से कम’ और ‘से अधिक’ प्रकार का संचयी आवृत्ति वितरण तैयार करो ।
उत्तर :
एक वर्ग की मध्यकिंमत 3 और वर्गलंबाई 6 है इसलिए उस वर्ग की अधःसीमाबिंदु और उर्ध्व सीमाबिंदु निम्नसूत्र से प्राप्त करेंगे ।

मध्यकिंमत हो ऐसा वर्ग 0 से 6 होगा । उस पर से शेष वर्ग बनाकर निवारक सतत (अखंडित) आवृत्ति वितरण निम्नानुसार प्राप्त करेंगे जिससे लघुतम मूल्य = – 10 और महत्तम मूल्य = 23 का समावेश हो ।
40 दिन के दौरान मिक्क्षर के उत्पादन की संख्या में परिवर्तन दर्शाता निवारक सतत ( अखंडित) आवृत्ति वितरण

प्रश्न 4.
एक विद्यालय के 30 विद्यार्थियों की ऊँचाई (सेमी में.) संबित निम्नलिखित सूचना पर से 6 वर्गों में विभाजित करके अनिवारक आवृत्ति वितरण तैयार कीजिए और उस पर ‘से कम’ और ‘से अधिक’ प्रकार का संचयी आवृत्ति वितरण तैयार कीजिए ।

आवृत्ति वितरण पर से निम्न प्रश्नों के उत्तर दीजिए ।
(1) यदि N.C.C. की प्रवृत्ति में हिस्सा लेने हेतु 160 सेमी ऊँचाई आवश्यक हो तो कितने विद्यार्थियों का इस प्रवृत्ति में चयन होगा ?
(2) विद्यार्थियों की ऊँचाई 153 से.मी. से 163 से.मी. के बीच हो ऐसे विद्यार्थियों की संख्या ज्ञात कीजिए।
(3) सब से कम ऊँचाईवाले तीसरे हिस्से के विद्यार्थियों की महत्तम ऊँचाई ज्ञात कीजिए ।
उत्तर :
यहाँ सबसे छोटा अवलोकन मूल्य 141 और सबसे महत्तम अवलोकन 168 मूल्य है ।
∴ विस्तार R = 168 – 141 = 27 होगा । K = 6 है
∴ वर्ग लंबाई (c) = \(\frac{\mathrm{R}}{\mathrm{K}}\)
= \(\frac{27}{6}\) = 4.5 = 5 का रखेंगे ।
आवृत्ति वितरण का प्रथम वर्ग 140 – 144 और अंतिम वर्ग 165 – 169 लेंगे ।
30 विद्यार्थियों की ऊँचाई (से.मी.में) दर्शाता अनिवारक आवृत्ति वितरण
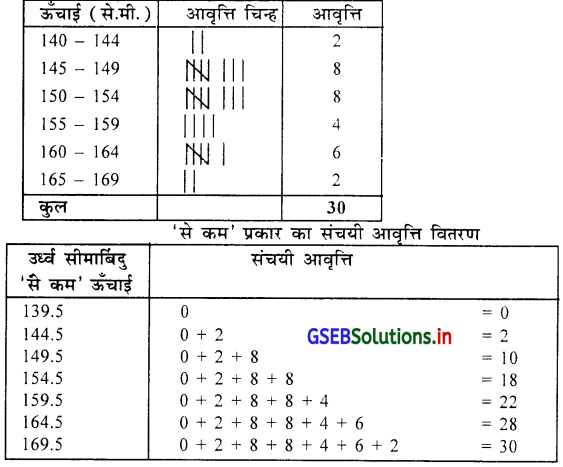
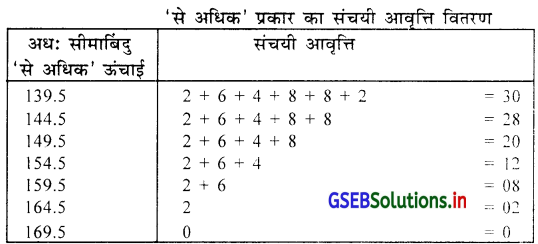
आवृत्ति वितरण पर से प्रश्नों के उत्तर :
(1) यदि N.C.C. की प्रवृत्ति के लिए 160 सेमी से अधिक ऊँचाईवाला विद्यार्थी हिस्सा ले सकते है ।
∴ ≥ 159.5 = 8 विद्यार्थी हिस्सा ले सकते है ।
(2) विद्यार्थियों की ऊँचाई 153 से 163 सेमी के बीच हो ऐले विद्यार्थी
∴ 153 150 से 154 के वर्ग में आता है और उस वर्ग की आवृत्ति 8 है। ∴ 5 = 8
∴ \(\frac{2 \times 8}{F}\) = 3.2 ∴ 2 = ?
155 – 159 की आवृत्ति 4 है ।
∴ 163 160 – 164 के वर्ग में आता है ।
∴ 5 = 6 आवृत्ति
2 = ?
\(\frac{2 \times 6}{5}\) = 2.4 × 2 = 4.8
∴ 153 से 163 के बीच ऊँचाईवाले विद्यार्थियों की संख्या – 3.2 + 4 + 4.8 :- 12 विद्यार्थी
(3) सबसे कम ऊँचाईवाले तीसरे हिस्से के विद्यार्थियों की महत्तम ऊँचाई 149 से.मी. होगी ।
प्रथम और दूसरा वर्ग की आवृत्ति 2 + 8 = 10 30 का तीसरा हिस्सा है ।
∴ 149 से.मी.
![]()
प्रश्न 5.
एक युनिवर्सिटी के विद्यार्थियों के विद्याशाखा और लिंग अनुसार वर्गीकरण से निम्नलिखित सूचना पर से योग्य सारणी की रचना कीजिए ।
कुल 40000 विद्यार्थियों में से 60% लड़के थे । एन्जिनियरींग शाखा में लड़कियों की संख्या वाणिज्य विद्याशाखा की लड़कियों की अपेक्षा तीन गुनी थी । मेडिकल शाखा में युनिवर्सिटी के कुल संख्या का 10% लड़कियाँ और 15% लड़के थे। विज्ञान शाखा में युनिवर्सिटी की कुल संख्या के 20% विद्यार्थी थे जिस में से लड़कियाँ लड़कों के सातवे जितनी था । जबकि विनयन शाखा में कुल संख्या का 7% लड़के और 17% लड़कियाँ थी । वाणिज्य शाखा में विद्यार्थियों की संख्या युनिवर्सिटी की कुल संख्या का 3.75% था जिसमें लड़के और लड़कियों का अनुपात 3:7 था ।
उत्तर :
यहाँ दो गुणधर्म दिए है ।
(1) विद्याशाखा : एन्जिनियरींग, मेडिकल, विज्ञान, विनयन, वाणिज्य
(2) लिंग : लड़के, लड़कियाँ
एक युनिवर्सिटी में विद्यार्थियों का विद्याशाखा और लिंग के अनुसार सारणी
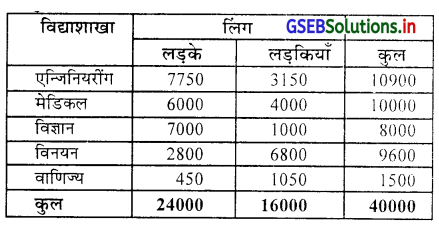
हल :
∴ युनिवर्सिटी में कुल 40000 विद्यार्थी हैं ।
∴ लड़कों की संख्या = \(\frac{40000 \times 60}{100}\) = 24000
∴ लड़कियों की संख्या = 40000 – 24000 = 16000
* मेडिकल विद्याशाखा में लड़कों की संख्या = \(\frac{40000 \times 15}{100}\) = 6000
लड़कियों की संख्या = \(\frac{40000 \times 10}{100}\) = 4000
∴ मेडिकल में कुल विद्यार्थिओं = 6000 + 4000 = 10000
* विज्ञानशाखा में कुल विद्यार्थिओं = \(\frac{40000 \times 20}{100}\) = 8000
लड़कों की संख्या से लड़कियाँ सातवे हिस्से की है ।
∴ लड़कों और लड़कियाँ का अनुपात = 7:1
∴ लड़के = \(\frac{8000 \times 7}{8}\) = 7000
∴ लडकियाँ = \(\frac{8000 \times 1}{8}\) = 1000
* विनयन शाखा में लड़कों की संख्या = \(\frac{40000 \times 7}{100}\) = 2800
∴ लड़कियों की संख्या = \(\frac{40000 \times 17}{100}\) = 6800
* वाणिज्य शाखा में कुल विद्यार्थियों = \(\frac{40000 \times 3.75}{100}\) = 1500
∴ वाणिज्य शाखा में लड़कों की संख्या = \(\frac{1500 \times 3}{100}\) = 450
∴ लड़कियों की संख्या = \(\frac{1500 \times 7}{100}\) = 1050
एन्जिनियरींग शाखा में लड़कियों की संख्या = 16000 – (4000 + 1000 + 6800 + 1050) = 16000 – 12850 = 3150