GSEB Solutions Class 11 Statistics Chapter 3 केन्द्रीय स्थिति के माप Ex 3.2

Gujarat Board Statistics Class 11 GSEB Solutions Chapter 3 केन्द्रीय स्थिति के माप Ex 3.2 Textbook Exercise Questions and Answers.

Gujarat Board Textbook Solutions Class 11 Statistics Chapter 3 केन्द्रीय स्थिति के माप Ex 3.2

प्रश्न 1.
एक फैक्टरी के 75 प्रतिशत कारीगरों को दिया जाता दैनिक वेतन का माध्य रु. 280 है, जबकि 125 अप्रशिक्षित कारीगरों का दैनिक वेतन का माध्य रु. 150 है । सभी कारीगरों के वेतन का माध्य ज्ञात करो ।
उत्तर :
यहाँ प्रशिक्षित = n₁ = 75 उसका माध्य = \(\bar{X}_1\) = 280
अप्रशिक्षित = n₂ = 125 उसका माध्य = \(\bar{X}_2\) = 150
सभी कारीगरों का वेतन का माध्य अर्थात् मिश्र माध्य
मिश्र माध्य \(\bar{X}_C=\frac{n_1 \bar{x}_1 \times n_2 \bar{x}_2}{n_1+n_2}\)
= \(\frac{75 \times 280+125 \times 150}{75+125}\) = \(\frac{21000+18750}{200}\) = \(\frac{39750}{200}\)
∴ \(\overline{\mathrm{X}}_c\) = 198.75 (रु.)
सभी कारीगरों के वेतन का माघ्य \(\overline{\mathrm{X}}_c\) = 198.75 रु. है ।

प्रश्न 2.
निम्न सूचना पर से मूल्य आधारित प्रतिशत परिवर्तन का माध्य ज्ञात करो ।

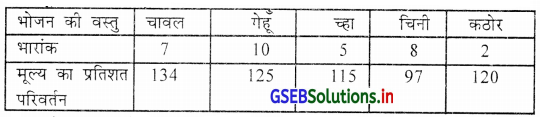
उत्तर :
यहाँ भारांक = w_i और मूल्य का प्रतिशत परिवर्तन x_i दिया है । दोनों का गुणाकार करके w_ix_i प्राप्त करेंगे ।

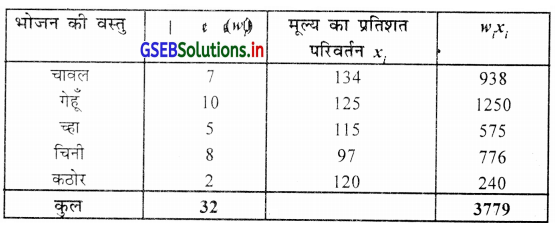
भोजन की वस्तु का मूल्य का भारांक और गुणाकार
भारित माध्य \(\bar{X}_w=\frac{\sum w_i x_j}{\sum w_i}=\frac{3779}{32}\) = 118.09 प्रतिशत परिवर्तन
वस्तु का मूल्य का प्रतिशत परिवर्तन = 118.09 है ।

प्रश्न 3.
एक ओफिस में कार्यरत 2 ओफिसर, 10 क्लर्क और 3 चपराशी स्टाफ पिकनिक के लिए हिस्सा देते है। प्रत्येक व्यक्ति का हिस्सा निम्नानुसार सारणी में है । उस पर से भारित माध्य ज्ञात करो ।

ओफिसर	क्लर्क	चपराशी
रु. 1000	रु. 500	रु. 200

उत्तर :
यहाँ भारांक w_i = 2, 10, 3 और चल x_i = 1000, 500, 200 है ।

भारित माध्य \(\bar{X}_w=\frac{\sum w_i x_i}{n}=\frac{7600}{15}\)
∴ भारित माध्य \(\bar{X}_w\) = 506.67
∴ भारित माध्य \(\bar{X}_w\) = 506.67 रु. है ।

प्रश्न 4.
एक विद्यार्थी को 7 थियरी पेपर में प्राप्त नंबर (गुण) का माध्य 62 है । 3 प्रेक्टिकल परीक्षा में उसके नंबर (गुण) का माध्य कितना होना चाहिए कि जिससे संपूर्ण परीक्षा का माध्य 68 होगा ? (प्रत्येक थियरी और प्रेक्टिकल परीक्षा के गुण समान है । )
उत्तर :
थियरी की 7 परीक्षा है । ∴ n₁ = 7
थियरी में प्राप्त नंबर (गुण) का माध्य 62 है । ∴ \(\bar{X}_1\) = 62
प्रेक्टिकल की 3 परीक्षा है । ∴ n₂ = 3
प्रेक्टिकल के नंबर (गुण) का माध्य ∴ \(\bar{X}_2\) = ?
संपूर्ण परीक्षा का माध्य अर्थात् मिश्र माध्य \(\bar{X}_c\) = 68

मिश्र माध्य \(\bar{X}_c\) – के सूत्र में उपर्युक्त किंमत रखने से \(\bar{X}_c\) प्राप्त होगा ।
∴ \(\bar{X}_c\) = \(\frac{n_1 \bar{x}_1+n_2 \bar{x}_2}{n_1+n_2}\)
68 = \(\frac{7 \times 62+3 \bar{X}_2}{7+3}\)
68 × 10 = 434 + 3\(\bar{X}_2\)
680 – 434 = 3\(\bar{X}_2\)
∴ \(\bar{X}_2\) = \(\frac{246}{3}\)
\(\bar{X}_2\) = 82 गुण (नंबर)
प्रेक्टिकल की परीक्षा में प्राप्त नंबर माध्य = 82 गुण (नंबर) है ।