GSEB Solutions Class 11 Statistics Chapter 3 केन्द्रीय स्थिति के माप Ex 3

Gujarat Board Statistics Class 11 GSEB Solutions Chapter 3 केन्द्रीय स्थिति के माप Ex 3 Textbook Exercise Questions and Answers.

Gujarat Board Textbook Solutions Class 11 Statistics Chapter 3 केन्द्रीय स्थिति के माप Ex 3

विभाग – A

1. निम्न दिये विकल्पों में से सही विकल्प पसंद करके लिखिए ।

प्रश्न 1.
कौन-सी औसत पर सबसे बड़ा और सबसे छोटा अवलोकन मूल्य का सबसे अधिक प्रभाव होता है ?
(A) समांतर माध्य
(B) मध्यका
(C) बहुलक
(D) गुणोत्तर माध्य
उत्तर :
(A) समांतर माध्य

प्रश्न 2.
निम्न में सो कौन-सा मूल्य हमे मध्यका देगा ?
(A) D₇
(B) Q₃
(C) P₄₅
(D) P₅₀
उत्तर :
(D) P₅₀

प्रश्न 3.
निम्न में से कौन से संयोगों में माध्य ज्ञात किया नहीं जा सकता ?
(A) वर्ग लंबाई असमान हो
(B) खुले शिरेवाला वर्ग हो
(C) वर्गों की संख्या 5 से अधिक हो
(D) अनिवारक प्रकार के वर्ग हो
उत्तर :
(B) खुले शिरेवाला वर्ग हो

प्रश्न 4.
किसी भी सूचना के लिए निम्न में से सही संबंध कौन-सा है ?
(A) \(\overline{\mathrm{x}}\) ≤ G
(B)\(\overline{\mathrm{x}}\) = G
(C) \(\overline{\mathrm{x}}\) ≥ G
(D) \(\overline{\mathrm{x}}\) > G
उत्तर :
(C) \(\overline{\mathrm{x}}\) ≥ G

प्रश्न 5.
औसत के आसपास समान रीति से विभाजित हुई सूचना के लिए निम्न में से कौन-सा परिणाम सत्य है ?
(A) \(\overline{\mathrm{x}}\) = M = M_O
(B) \(\overline{\mathrm{x}}\) > M > M_O
(C) \(\overline{\mathrm{x}}\) < M < M_O
(D) \(\overline{\mathrm{x}}\) < M > M_O
उत्तर :
(A) \(\overline{\mathrm{x}}\) = M = M_O

प्रश्न 6.
यदि 10 अवलोकनों का माध्य 15 हो, तो अवलोकन का योग कितना होगा ?
(A) 25
(B) 150
(C) 5
(D) 1.5
उत्तर :
(B) 150

प्रश्न 7.
अवलोकनों की सूचना के लिए Σ (x – 9) = 0 हो, तो माध्य की कीमत कितनी होगी ?
(A) \(\overline{\mathrm{x}}\) = 0
(B) \(\overline{\mathrm{x}}\) = 5
(C) \(\overline{\mathrm{x}}\) = 9
(D) \(\overline{\mathrm{x}}\) = 45
उत्तर :
(C) \(\overline{\mathrm{x}}\) = 9

प्रश्न 8.
अवलोकनों 7, 9, 9, 1, 7, 9, 4, 9, 1 का बहुलक क्या होगा ? ।
(A) 1
(B) 4
(C) 7
(D) 9
उत्तर :
(D) 9

प्रश्न 9.
अवलोकनो के समूह में मध्यका अर्थात् क्या ?
(A) 25 वाँ अवलोकन का मूल्य
(B) 26 वाँ अवलोकन का मूल्य
(C) 25.5 वाँ अवलोकन का मूल्य
(D) 26.5 वा अवलोकन का मूल्य
उत्तर :
(C) 25.5 वाँ अवलोकन का मूल्य

प्रश्न 10.
4 और 9 का गुणोत्तर माध्य कितना होगा ?
(A) 4
(B) 6
(C) 6.5
(D) 36
उत्तर :
(B) 6

प्रश्न 11.
एक चल का माध्य 15 और मध्यका 20 हो तो आच्छादित सूत्र से बहुलक कितना होगा ?
(A) 30
(B) 5
(C) 35
(D) 17.5
उत्तर :
(A) 30

प्रश्न 12.
10 अवलोकनों की मध्यका 14 है, यदि प्रत्येक अवलोकन दो गुना किया जाए तो प्राप्त अवलोकनों की मध्यका कितनी होगी?
(A) 10
(B) 28
(C) 7
(D) 1.4
उत्तर :
(B) 28

प्रश्न 13.
एक सूचना के सभी अवलोकन का समान मूल्य 16 है तो भूयिष्ठक कितना होगा ?
(A) 8
(B) 2
(C) 16
(D) 4
उत्तर :
(C) 16

प्रश्न 14.
निम्न में से कौन-सा विधान असत्य है ?
(A) चतुर्थकों द्वारा सूचना के अवलोकन 4 हिस्सों में विभाजित है ।
(B) माध्य दी गई सूचना के अवलोकनों का दो हिस्सा करता है ।
(C) शतमक दी गई सूचना के अवलोकनों का 100 हिस्सा करता है ।
(D) दशमक दी गई सूचना के अवलोकनों का 10 हिस्सा करता है।
उत्तर :
(B) माध्य दी गई सूचना के अवलोकनों का दो हिस्सा करता है ।

प्रश्न 15.
स्टील की पाइप बनानेवाली एक कंपनी के 6 पाइपों के लंबाई (मीटर) निम्नानुसार है ।
1.05, 1.15, 0.98, 1.12, 0.89, 0.95
निम्न में से कौन-सा विधान सत्य है ?
(A) भूयिष्ठक = 1 मीटर
(B) भूयिष्ठक = 1.15 मीटर
(C) भूयिष्ठक = 0.98 मीटर
(D) भूयिष्ठक प्राप्त नहीं हैं
उत्तर :
(D) भूयिष्ठक प्राप्त नहीं हैं

विभाग – B

निम्न प्रश्नों के एक वाक्य में उत्तर दीजिए ।

प्रश्न 1.
माध्य का कोई भी एक लाभ बताइए ।
उत्तर :

1. माध्य की परिभाषा स्पष्ट व निश्चित है ।
2. इसकी गणना में सभी अवलोकनों का उपयोग होता है ।

प्रश्न 2.
यदि अवलोकनों का महत्त्व भिन्न-भिन्न हो तो कौन-सी औसत का उपयोग करना चाहिए ?
उत्तर :
यदि अवलोकनों का महत्त्व भिन्न भिन्न हो तो भारित माध्य का उपयोग करना चाहिए ।

प्रश्न 3.
कोई भी दो स्थानीय औसत के नाम दीजिए ।
उत्तर :
मध्यका, प्रथम चतुर्थक, तृतीय चतुर्थक, दशमक तथा शतमक सह स्थानीय माप है ।

प्रश्न 4.
माध्य, मध्यका और भूयिष्ठक के बीच का अनुमानितता युक्त (आच्छादित) सूत्र लिखिए ।
उत्तर :
\(\overline{\mathrm{x}}\), M का उपयोग करके भूयिष्ठक का अनुमानितता युक्त M_O = 3M – 2\(\overline{\mathrm{x}}\)

प्रश्न 5.
कौन-सी परिस्थिति में गुणोत्तर माध्य ज्ञात नहीं हो सकता ?
उत्तर :
यदि सूचना का एकाध अवलोकन शून्य अथवा ऋण हो तो गुणोत्तर माध्य ज्ञात नहीं हो सकता ।

प्रश्न 6.
भूयिष्ठक की परिभाषा दीजिए ।
उत्तर :
सूचना के अवलकनों की श्रृंखला में जिस अवलोकन का मूल्य सबसे अधिक बार पुनरावर्तित होता है, उस मूल्य को सूचना का भूयिष्ठक कहते है ।

प्रश्न 7.
माध्य, मध्यका, भूयिष्ठक के बीच का अनुमानितता युक्त (आच्छादित) सूत्र देनेवाले आंकडाशास्त्री का नाम दीजिए ।
उत्तर :
माध्य, मध्यका, बहुलक के बीच का अनुमानितता युक्त सूत्र देनेवाले आंकडाशास्त्री कार्लपियर्सन है ।

प्रश्न 8.
10 अवलोकनों का मध्यका (M) 55 है । यदि महत्तम अवलोकन का मूल्य 100 से बढ़कर 110 हो, तो मध्यका (M) का नया मूल्य ज्ञात करो।
उत्तर :
मध्यका M = 55 होगा क्योंकि मध्यका (M) पर अंतिम अवलोकन का प्रभाव होता नहीं है ।

प्रश्न 9.
एक चल x का माध्य \(\overline{\mathrm{x}}\) = 17 है । चल y = x – 4 का माध्य कितना होगा ?
उत्तर :
y = x – 4 का माध्य \(\overline{\mathrm{x}}\) = 17 – 4 = 13
∴ y = x – 4 का माध्य 13 होगा ।

प्रश्न 10.
निम्न आवृत्ति वितरण का भूयिष्ठक ज्ञात करो ।

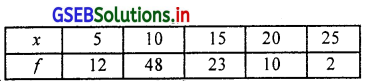
उत्तर :
यहाँ असतत (खंडित) आवृत्ति वितरण है। इसलिए भूयिष्ठक महत्तम आवृत्ति 48 के अनुरूप अवलोकन 10 है ।
∴ भूयिष्ठक M_O = 10

प्रश्न 11.
दो संख्याओं का माध्य 5 है । यदि एक संख्या 6 हो तो दूसरी संख्या ज्ञात कीजिए ।
उत्तर :
यहा n = 2 \(\overline{\mathrm{x}}\) = 5
∴ \(\overline{\mathrm{x}}\) = \(\frac{\sum x}{n}\), 5 = \(\frac{\sum x}{2}\)
∴ Σx = 10
एक संख्या 6 है ∴ x = 6
∴ दूसरी संख्या y = 10 – 6 = 4

दूसरी विधि :
मानाकि एक संख्या x = 6 है तो दूसरी संख्या y = ?
5 = \(\frac{x+y}{02}\) ∴ 5 × 2 = 6 + y, 10 – 6 = y ∴ y = 4

प्रश्न 12.
अवलोकन 15, 4, 7, 20, 2, 7, 13 के लिए प्रथम चतुर्थक (Q₁) ज्ञात कीजिए ।
उत्तर :
प्रथम चतुर्थक (Q₁) ज्ञात करने के लिए सर्वप्रथम अवलोकनों को चढ़ते क्रम में गठित करने पर चढ़ते क्रम 2, 4, 7, 7, 13, 15, 20
Q₁ = \(\frac{n+1}{4}\) वाँ अवलोकन मूल्य
Q₁ = \(\frac{7+1}{4}=\frac{8}{4}\) = 2 वा अवलोकन मूल्य चढ़ते क्रम में 4 है ।
∴ Q₁ = 4

प्रश्न 13.
खुल्ला शिरावाले वर्गों हो तो सतत आवृत्ति वितरण के लिए केन्द्रिय स्थिति के लिए कौन-सी औसत ज्ञात की जा सकती है ?
उत्तर :
खुल्ला शिरावाला आवृत्ति वितरण हो तो केन्द्रिय स्थिति का योग्य माप मध्यका है ।

प्रश्न 14.
एक चल के लिए Q₃ = 25.75 हो तो P₇₅ ज्ञात कीजिए ।
उत्तर :
Q₃ आवृत्ति वितरण के या चल मूल्यों के 75 प्रतिशत अवलोकन से कम है इसलिए P₇₅ = Q₃ होता है। ∴ P₇₅ = 25.75 होगा ।

प्रश्न 15.
एक फेरिवाले की प्रतिदिन माँग की मध्यका 15 प्राप्त है । यदि वह प्रत्येक वस्तु रु. 10 के मूल्य से बेचे तो उसकी आय की माध्यिका (M) कितनी होगी ?
उत्तर :
मार्ग की मध्यका M = 15 है इसलिए प्रत्येक वस्तु 10 रु. के मूल्य से बेचे तो उसकी आय की मध्यका M = 15 × 10 = 150 होगा । ∴ M = 150 बिक्री की मध्यका

विभाग – C

निम्न प्रश्नों के उत्तर दीजिए ।

प्रश्न 1.
भारित माध्य की परिभाषा दीजिए।
उत्तर :
अलग अलग अवलोकन का महत्त्व अलग – अलग होता है। जिससे गणना करते समय उसके महत्त्व को ध्यान में लेना चाहिए । अवलोकन के महत्त्व को भार कहा जाता है । इस प्रकार भार को ध्यान में लेकर माध्य ज्ञात किया जाए तो उसे भारित माध्य (Weighted Mean) कहा जाता है ।

प्रश्न 2.
केन्द्रिय स्थिति के माप का अर्थ समझाइए ।
उत्तर :
भिन्न भिन्न आवृत्ति वितरण के लिए खिचा गया आलेखो में ज्यादातर आलेखो में हम एक सामान्य रीति से देख सकते हैं. कि चल का मूल्य किसी विशिष्ट केन्द्रिय मूल्य के आसपास संकलित है। सूचना के ऐसे लक्षण को केन्द्रिय स्थिति (Central Tendency) कहते है । जो केन्द्रीय मूल्य के आसपास चल का मूल्य संकलित हो उस मूल्य को केन्द्रीय स्थिति का माप (Measure of Central Tendency) कहते है।

प्रश्न 3.
भूयिष्ठक के गुण (लाभ) बताइए ।
उत्तर :
भूयिष्ठक के गुण निम्नलिखित है :

1. इसकी परिभाषा व अर्थ समझने में सरल है ।
2. केवल निरीक्षण से ही बहुलक का मूल्य ज्ञात हो जाता है।
3. इसका मूल्य आलेख द्वारा निर्धारित किया जा सकता है ।
4. इस पर सीमान्त अवलोकनों का प्रभाव कम पड़ता है।
5. अवर्गीकृत सूचना व खंडित (असतत) श्रृंखला में इसको मूल्य सूचना के किसी एक अवलोकन के मूल्य के बराबर होता है।

प्रश्न 4.
मिश्र माध्य समझाइए ।
उत्तर :
अलग अलग समूहों के माध्य पर से समग्र समूहों का एक माध्य निकाला जाता है उसे मिश्र माध्य कहते है । दो या उससे अधिक समूहों को एकत्रित करके संयुक्त माध्य निकाला जाता है, जिसे मिश्र माध्य कहते हैं, उसे संकेत में \(\bar{X}_c\) द्वारा दर्शाया जाता है ।

यदि K समूहों के भिन्न भिन्न माध्य क्रमशः \(\overline{\mathrm{X}}_1, \overline{\mathrm{X}}_2\) ……. \(\bar{X}_k\) हो और संख्या क्रमशः n₁ n₂,……n_k हो तो समग्र समूह का मिश्र माध्य \(\bar{X}_c\) निम्नलिखित सूत्र से मिलता है ।
मिश्र माध्य \(\overline{\mathrm{X}}_c=\frac{n_1 \bar{x}_1+n_2 \bar{x}_2+\ldots .+n_k \bar{x}_k}{n_1+n_2+\ldots \ldots+n_k}\)

प्रश्न 5.
कौन से प्रकार की सूचना में माध्य से मध्यका का माप अधिक योग्य माप है ?
उत्तर :
यदि अवलोकन औसत के आसपास समान रीति से विभाजित हो और उसमें अत्यंत बडे या अत्यंत छोटे अवलोकन न हो तो माध्य श्रेष्ठ माना जाता है । यदि इस शरतों का समाधान न होता हो तो माध्य सूचना का योग्य प्रतिनिधित्व नहि कर सकता है । ऐसी परिस्थिति में योग्य माप मध्यका है ।

प्रश्न 6.
योग्य औसत का चयन करते समय कोन से मुद्दे ध्यान में रखना चाहिए ?
उत्तर :
योग्य औसत का चयन करते समय निम्न मुद्दों को ध्यान में रखना चाहिए :

1. सूचना का अवलोकन का स्वरूप को ध्यान में रखकर औसत का चयन करना चाहिए ।
2. सूचना के चल मूल्य पर से अभ्यास के अंतर्गत चल लक्षण के मूल्य को ध्यान में रखना चाहिए ।
3. अभ्यास का उद्देश्य क्या है उसे ध्यान में रखकर योग्य औसत का चयन किया जाता है ।
4. सूचना के वर्गीकरण का प्रकार को ध्यान में रखकर औसत का चयन किया जाता है ।
5. उच्चत्तर अभ्यास में कौन-सी औसत की आवश्यकता है उसे ध्यान में रखकर औसत का चयन किया जाता है ।

प्रश्न 7.
एक चल का माध्य और भूयिष्ठक क्रमशः 5.5 और 6.4 है । मध्यका का मूल्य ज्ञात करो ।
उत्तर :
यहाँ \(\bar{X}\) = 5.5 और M_O = 6.4 है ।
अनुमानितायुक्त सूत्र M_O = 3M – 2\(\bar{X}\) में \(\bar{X}\) = 5.5, Mo = 6.4 रखने पर
6.4 = 3M – 2 (5.5)
6.4 = 3M – 11
6.4 + 11 = 3M
∴ 3M = 17.4
∴ M = \(\frac{17.4}{3}\)
∴ मध्यका M = 5.8

प्रश्न 8.
दो संख्या का गुणोत्तर माध्य 8 है । यदि प्रथम संख्या 4 हो तो दूसरी संख्या ज्ञात कीजिए ।
उत्तर :
यहाँ G = 8 है मानाकि दो संख्या x₁ और x₂ है ।
प्रथम संख्या 4 है ∴ x₁ = 4 दूसरी संख्या ज्ञात करने के लिए G = \(\sqrt{x_1 x_2}\) में मान रखने पर
8 = \(\sqrt{4 \times x_2}\) (दोनों ओर वर्ग करने पर)
64 = 4 × x₂
∴ x₂ = \(\frac{64}{4}\) ∴ दूसरी संख्या 16 होगी ।
x₂ = 16

प्रश्न 9.
एक कारखाना के साप्ताहिक उत्पादन (x) का माध्य = 81 इकाई है । यदि उत्पादन खर्च y = 3x + 50 हो तो खर्च का माध्य ज्ञात कीजिए।
उत्तर :
साप्ताहिक उत्पादन का माध्य 81 है । ∴ x = 81
उत्पादन खर्च y = 3x + 50 में x = 81 रखने पर
y = 3 (81) + 50
y = 243 + 50
∴ y = 293
खर्च का माध्य 293 होगा ।

प्रश्न 10.
अवलोकन a – 5, a + 1, a + 2, a – 3 और a की मध्यका 10 है । a का मूल्य ज्ञात करो ।
उत्तर :
अवलोकन को चढ़ते क्रम में गठित करने पर
a – 5, a – 3, a, a + 1, a + 2
मध्यका M = \(\frac{n+1}{2}\) (सूचना अवर्गीकृत है ।)
= \(\frac{5+1}{2}\) वा अवलोकन मूल्य
= \(\frac{6}{2}\) = 3 वा अवलोकन
मूल्य तीसरा अवलोकन मूल्य a है ∴ M = a, 10 = a, ∴ a = 10
a का मूल्य 10 है ।

प्रश्न 11.
एक कक्षा के 40 विद्यार्थिओं के गणित विषय में प्राप्त गुण (नंबर ) का माध्य 76 है, जबकि दूसरी कक्षा के 50 विद्यार्थियों का नंबर का माध्य 85 है। दोनों कक्षा के विद्यार्थियों गणित विषय के नंबर (गुण) का माध्य ज्ञात करो ।
उत्तर :
प्रथम कक्षा की संख्या को n₁ ∴ n₁ = 40
प्रथम कक्षा का माध्य को \(\overline{\mathrm{X}}_1\) ∴\(\overline{\mathrm{X}}_1\) = 76
दूसरी कक्षा की संख्या को n₂ ∴ n₂ = 50
दूसरी कक्षा का माध्य को \(\overline{\mathrm{X}}_2\) ∴ \(\overline{\mathrm{X}}_2\) = 85
तो मिश्र माध्य \(\overline{\mathrm{X}}_c\) के सूत्र में रखने पर
मिश्र माध्य \(\overline{\mathrm{X}}_c\) = \(\frac{n_1 \bar{X}_1+n_2 \bar{X}_2}{n_1+n_2}\) = \(\frac{40 \times 76+50 \times 85}{40+50}\)
= \(\frac{3040+4250}{90}=\frac{7290}{90}\) = 81 गुण
दोनों कक्षा के गणित विषय का मिश्र माध्य = 81 गुण है ।

प्रश्न 12.
एक विस्तार के परिवारों में प्रति परिवार परिवहन की संख्या निम्न सारणी में दी है। परिवहन की संख्या का मध्यका ज्ञात कीजिए ।

उत्तर :
मध्यका M ज्ञात करने के लिए संचयी आवृत्ति वितरण प्राप्त करेंगे ।

परिवहनों की संख्या x	परिवारों की संख्या (f)	संचयी आवृत्ति
0	2	2
1	4	6
2	9	15
3	7	22
4	3	25
	25

मध्यका M = \(\frac{n+1}{2}\) वाँ अवलोकन मूल्य
= \(\frac{25+1}{2}\)
= \(\frac{26}{2}\) = 13 वाँ अवलोकन मूल्य संचयी आवृत्ति वितरण में देखने पर 13 के समक्ष का अवलोकन 2 है ।
∴ M = 2
प्रतिपरिवार परिवहन की संख्या का मध्यका M = 2 होगा ।

प्रश्न 13.
निम्न सूचना पर से चल x का भारित माध्य ज्ञात करो ।

चल x	1500	800	200
भारांक w	5	4	1

उत्तर :
भारित माध्य ज्ञात करने के लिए निम्न सारणी बनायेंगे ।

चल xi	भारांक wi	wi xi
1500	5	7500
800	4	3200
200	1	200
कुल	10	10900

भारित माध्य \(\bar{X}_w\) = \(\frac{\sum w_i x_i}{\sum w_i}=\frac{10900}{10}\)
∴ भारित माध्य \(\bar{X}_w\) = 1090

विभाग – D

निम्न प्रश्नों के उत्तर दीजिए ।

प्रश्न 1.
आदर्श औसत के लक्षण बताइए ।
उत्तर :
आदर्श औसत के लक्षण निम्नलिखित है :

1. औसत की परिभाषा स्पष्ट और स्थिर होनी चाहिए ।
2. वह माप समझने में सरल होना चाहिए ।
3. उसकी गणना सरल होनी चाहिए ।
4. उसकी गणना में सूचना के सभी अवलोकनों का उपयोग होना चाहिए ।
5. यह माप अन्य गणितीय व बीज गणितीय क्रियाओं के लिए अनुकूल होना चाहिए ।
6. आंकडाशास्त्र के उच्च अभ्यास में इस माप की उपयोगिता होनी चाहिए ।
7. यह माप स्थायी होना चाहिए अर्थात् एक ही समष्टि में से एक ही आकार के अलग-अलग न्यादर्श लिए जाय तो उनमें से प्राप्त औसत का मूल्य लगभग एकसमान होना चाहिए ।
8. यह माप दी गई सूचना का योग्य प्रतिनिधित्व करे ऐसा होना चाहिए ।
9. उसकी किंमत वास्तविक होनी चाहिए ।
10. कुछ बड़े मूल्य या छोटे मूल्य के अवलोकनों का अधिक प्रभाव नहीं होना चाहिए ।

प्रश्न 2.
गुणोत्तर माध्य की परिभाषा दीजिए और उसके लाभ (गुण) तथा अवगुण बताइए ।
उत्तर :
यदि n धन संख्याओं की श्रृंखला x₁, x₂….x_n दी गई हो तो शृंखला की n संख्याओं के गुणाकार का n वाँ मूल्य शृंखला का गुणोत्तर माध्य (Geometric Mean) कहलाता है । इसे संकेत में G द्वारा प्रदर्शित करते है ।

गुणोत्तर माध्य के गुण – अवगुण :
गुण :

1. इसकी परिभाषा स्पष्ट और सटीक है ।
2. इसकी गणना में सभी अवलोकनों का उपयोग होता है ।
3. बीजगणितीय विवेचन के लिए यह माप अनुकूल है ।
4. यह स्थिर माप है।
5. निर्देशांक जैसे प्रश्नों के लिए बहुत उपयोगी माप है ।
6. इसकी गणना में सीमान्त अवलोकन मूल्यों का प्रभाव नहीं पड़ता है ।

अवगुण :

1. गुणोत्तर माध्य की गणना कठिन व जटिल है।
2. गुणोत्तर माध्य को आलेख द्वारा ज्ञात नहीं कर सकते है ।
3. निर्वतमुखी (खुले शिरावाला) आवृत्ति वितरण पर से गुणोत्तर माध्य ज्ञात नहीं हो सकता है ।
4. दी गई सूचना का एकाध अवलोकन का मूल्य शून्य या ऋण हो तो गुणोत्तर माध्य की गणना नहीं की जा सकती है ।

प्रश्न 3.
केन्द्रीय स्थिति के माप के रूप में भूयिष्ठक का अर्थ उदाहरण सहित समझाइए ।
उत्तर :
सूचना के अवलोकनों की श्रृंखला में जिस अवलोकन का मूल्य सबसे अधिक बार पुनरावर्तित होता है, उस मूल्य को उस सूचना का भूयिष्ठक कहते है । उसे संकेत में M_O द्वारा प्रदर्शित किया जाता है ।

उदा. :

1. विद्यालय के विद्यार्थियों को औसत 4 भाषाएँ आती है ।
2. अपने देश में स्त्रियों की औसत ऊँचाई 1.4 मीटर है।
3. जूते बनानेवाली कंपनी का प्रतिदिन उत्पादन 500 जूतों का है ।
4. विद्यार्थियों की औसत ऊँचाई 140 से.मी. है।
   यहाँ औसत के रूप में भूयिष्ठक का उपयोग होता है ऐसा कहा जाता है ।

प्रश्न 4.
स्थानीय औसत को समझाइए ।
उत्तर :
यदि अवलोकन औसत के आसपास समान रीति से विभाजित हो और उसमें बड़े और छोटे अवलोकन न हो तो माध्य योग्य माना जाता है । लेकिन यह शर्त का पालन न होता हो तो माध्य योग्य प्रतिनिधित्व नहीं कर सकता है। ऐसी परिस्थिति में एक अन्य माप औसत का मध्यका है उसे स्थानीय माप कहते हैं । मध्यका के अलावा चतुर्थक, दशमक और शतमक भी एक स्थानीय माप है ।

दी गई सूचना का मूल्यों को चढ़ते क्रम में गठित करने पर किसी एक निश्चित स्थान पर आनेवाले अवलोकनों का उपयोग करके मध्यका, चतुर्थकों, दशमक और शतमक के मुल्य ज्ञात किए जाते है । उस औसत को स्थानीय औसत कहते है ।

प्रश्न 5.
केन्द्रीय स्थिति के माप के रूप में मध्यका और मध्यक की तुलना कीजिए ।
उत्तर :
मध्यका M सूचना को चढ़ते या उतरते क्रम में गठित करने पर ठीक मध्य में आता अवलोकन को ध्यान में लिया जाता है। अर्थात् सूचना के 50% अवलोकन मध्यका से कम मूल्य और 50% अवलोकन सूचना के मध्यका से मूल्यवाले होते है । उस पर अंतिम अवलोकनों का प्रभाव नहीं होता है ।

माध्य की गणना में सभी अवलोकनों का उपयोग होता है इसलिए केन्द्रीय स्थिति का योग्य माप है । लेकिन आवृत्ति वितरण निर्वतमुखी (खुल्ले शीरावाला) हो तब मध्यका योग्य माप माना जाता है । उस पर से माध्य ज्ञात नहीं हो सकता ।

प्रश्न 6.
कौन-सी औसत को श्रेष्ठ औसत कहते है ? क्यों ?
उत्तर : माध्य को केन्द्रीय स्थिति के मापों में श्रेष्ठ औसत कहते है क्योंकि माध्य में सभी अवलोकनों का और सभी वर्गों का उपयोग करके प्राप्त की जाती है । प्रथम और अंतिम सभी अवलोकनों का उपयोग होने से औसत के रूप में माध्य श्रेष्ठ है ।

औसतें दूसरे माप मध्यका, चतुर्थकों, दशांशकों, शतमकों की गणना में सूचना के सभी अवलोकनों का उपयोग नहीं होता है इसलिए समग्र सूचना का प्रतिनिधित्व नहीं कर सकता है।
जब आवृत्ति वितरण निर्वतमुखी हो तब मध्यका औसत के लिए योग्य माप है ।

प्रश्न 7.
एक राज्य के चार वर्षों का आर्थिक विकास दर क्रमशः 2%, 2.5%, 4%, 3% है। योग्य औसत का उपयोग करके औसत विकासदर ज्ञात कीजिए ।
उत्तर :
यहाँ चार राज्यों का विकासदर प्रतिशत में दिया है इसलिए औसत के लिए गुणोत्तर माध्य का उपयोग करेंगे ।
विकासदर के प्रतिशत को ध्यान में लेने पर अवलोकन निम्नानुसार प्राप्त होंगे ।
x₁ = 100 + 2 = 102 x₂ = 100 + 2.5 = 102.5
x₃ = 100 + 4 = 104 x₄ = 100 + 3 = 103
G = \(\sqrt[4]{x_1 \times x_2 \times x_3 \times x_4}\)
= \(\sqrt[4]{102 \times 104 \times 102.5 \times 103}=\sqrt[4]{111993960}\)
= \(\sqrt{1058271989}\) = 102.87
∴ चार राज्यों का विकासदर 2.87% गुणोत्तर माध्य

प्रश्न 8.
मोबाइल की दुकान के प्रतिदिन बिक्री की निम्न सूचना पर से D₇ और P₁₅ ज्ञात करो और उसका अर्थघटन करो ।

उत्तर :
D₇ और P₁₅ ज्ञात करने के लिए संचयी आवृत्ति प्राप्त करेंगे । उसे निम्न सारणी में दर्शायेंगे ।

मोबाइल फोन की संख्या x	दिनों की संख्या f	संचयी आवृत्ति cf
4	3	3
6	9	12
7	15	27
8	23	50
10	8	58
12	2	60

D₇ = \(\frac{j(n+1)}{10}\) वाँ अवलोकन मूल्य = \(\frac{7(60+1)}{10}\)
= \(\frac{7 \times 61}{10}\) = 42.7 वाँ अवलोकन मूल्य cf की सारणी. में देखने पर 42.7 के समक्ष का अवलोकन 8 है ।
∴ D₇ = 8 मोबाइल फोन
अर्थघटन : 70% दिनों का विक्रय 8 या उससे कम मोबाइल फोन का होगा ।
⇒ P₁₅ = \(\frac{j(n+1)}{100}\) वाँ अवलोकन मूल्य
= \(\frac{15(60+1)}{100}=\frac{15 \times 61}{100}\)
= 9.15 वाँ अवलोकन मूल्य cf की सारणी में देखने पर 9.15 के समक्ष का चरमूल्य 6 है ।
∴ P₁₅ = 6 मोबाइल फोन
अर्थघटन : 15% दिनों का विक्रय 6 या उससे कम मोबाइल फोन का होगा ।

प्रश्न 9.
एक परफ्युम उत्पादक के मशीन से भरी गई बोटलों में परफ्युम का मात्रा की माध्य 29.6 मिलि और 30.4 मिलि के बीच होना चाहिए । जाँच के लिए 7 बोटलों में परफ्युम की मात्रा (मिलि में) निम्नानुसार है ।
30.2, 28.9, 29.2, 30.1, 29.4, 31.3, 31.4
क्या मशीन उचित रीति से कार्य करता है ?
उत्तर :
7 बोटलों का माध्य ज्ञात करेंगे । सूचना अवर्गीकृत है । यहाँ n = 7
इसलिए माध्य \(\overline{\mathrm{X}}=\frac{\sum x}{n}\) सूत्र का उपयोग करेंगे ।

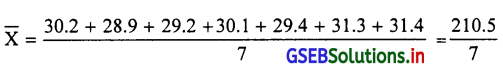
\(\bar{X}\) = 30.07 मि.लि.
मशीन योग्य रीति से कार्य करता है क्योंकि माध्य 29.6 मिलि और 30.4 मिलि के बीच प्राप्त होता है ।

प्रश्न 10.
एक कक्षा के 34 लड़कों का नंबर का माध्य 57 है । उसी वर्ग के सभी 60 विद्यार्थियों का नंबर का माध्य 59 है, तो लड़कियों के नंबर का माध्य ज्ञात करो ।
उत्तर :
लड़कों को प्रथम समूह मानने पर उसकी संख्या 34 को n₁ ∴ n₁ = 34
लड़कों का नंबर का माध्य 57 है । ∴ \(\bar{X}_1\) = 57
लड़कियों को दूसरा समूह मानने पर उसकी संख्या (60 – 34) = 26 को n₂ ∴ n₂ = 26
लड़कियों के माध्य को \(\bar{X}_2\) कहे तो ∴ \(\bar{X}_2\) = ?
सभी 60 विद्यार्थियों का माध्य दिया है अर्थात् मिश्रमाध्य \(\bar{X}_c\) = 59 है ।
∴ मिश्रमाध्य के सूत्र का उपयोग करेंगे ।

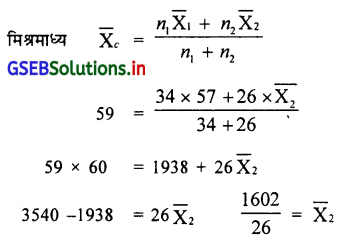
\(\bar{X}_2\) = 61.62 गुण (नंबर)
लड़कियों के नंबर का माध्य 61.62 होगा ।

प्रश्न 11.
एक सूचना में 50 अवलोकन का माध्य का मूल्य 35 था। बाद में मालूम हुआ कि एक अवलोकन का मूल्य 50 लिया गया था जो गलत था । तो यह अवलोकन को घटाया जाए तो शेष अवलोकनों का माध्य ज्ञात कीजिए ।
उत्तर :
यहाँ.n = 50, \(\overline{\mathrm{X}}\) = 35 है, गलत अवलोकन 50 है
∴ \(\bar{X}=\frac{\sum x}{n}\)
35 = \(\frac{\sum x}{50}\)
Σx = 35 × 50 ∴ Σx = 1750
एक अवलोकन गलत 50 लिया गया है । उसे Σx = 1750 में घटाने पर
Σx = 1750 – 50 = 1700
अब एक अवलोकन घटाने पर n = 50 – 1 = 49
∴ 49 अवलोकनों का माध्य \(\overline{\mathrm{X}}\) = \(\frac{1700}{49}\) = 34.69
∴ 49 अवलोकनों का नया माध्य = 34.69

प्रश्न 12.
अर्थशास्त्र विषय की परीक्षा में एक समूह के 18 विद्यार्थियों में से 3 विद्यार्थी अनुत्तीर्ण हुए । उत्तीर्ण हुए 15 विद्यार्थियों के गुण (नंबर) निम्नानुसार है । उस पर से सभी 18 विद्यार्थियों के गुण (नंबर) की मध्यका ज्ञात करो ।
42, 65, 53, 75, 43, 50, 68, 57, 79, 48, 51, 61, 55, 70, 64
उत्तर :
3 विद्यार्थी अनुतीर्ण है, इसलिए तीन विद्यार्थियों के नंबर चढ़ते क्रम में गठन करने पर प्रथम लिखेंगे । चढ़ते क्रम के गठन करने पर प्रथम तीन विद्यार्थियों के नंबर 42, 43, 48, 50, 51, 53, 55, 57, 61, 64, 65, 68, 70, 75, 79
M = \(\frac{n+1}{2}\) वाँ अवलोकन मूल्य
= \(\frac{81+1}{2}=\frac{19}{2}\) = 9.5 वाँ अवलोकन मूल्य
∴ M =
= \(\frac{53+55}{2}=\frac{108}{2}\)
∴ M = 54 गुण (नंबर)
सभी 18 विद्यार्थियों की मध्यका 54 गुण (नंबर) है ।

प्रश्न 13.
एक कंपनी के प्रतिदिन बिक्री का माध्य 126.2 है । एक नई विज्ञापन नीति का स्वीकार करने पर 10 दिनों के बिक्री की निम्न सूचना है ।
156, 125, 162, 153, 130, 124, 127, 142, 149, 121
क्या नई विज्ञापन नीति से बिक्री के माध्य में वृद्धि हुई है ऐसा कह सकते है ?
उत्तर :
पुराना माध्य = 126.2 है अब नई विज्ञापन नीति से 10 दिनों की बिक्री का माध्य के लिए
\(\overline{\mathrm{X}}=\frac{\sum \mathrm{x}}{\mathrm{n}}\) सूत्र का उपयोग करेंगे ।
यहाँ n = 10
Σx = 156 + 125 + 162 + 153 + 130 + 124 + 127 + 142 + 149 + 121
Σx = 1389
∴ \(\bar{X}=\frac{1389}{10}\) = 138.9 इकाई
पुराना माध्य 126.2 था । विज्ञापन नीति के बाद बिक्री के माध्य 138.9 मिला जिससे विज्ञापन नीति से बिक्री के माध्य में वृद्धि हुई है ।

विभाग – E

निम्न प्रश्नों के हल प्राप्त करो ।

प्रश्न 1.
भिन्न भिन्न परिवारों में बिजली के उपयोग की युनिट की संख्या निम्न सारणी में है । उस पर से उपयोग के युनिटों की संख्या का मध्यका ज्ञात कीजिए ।

उत्तर :
आवृत्ति वितरण खुल्ले शिरावाला है । आवृत्ति वितरण पर से संचयी आवृत्ति वितरण प्राप्त करेंगे ।

युनिट की संख्या	परिवारों की संख्या (f)	संचयी आवृत्ति cf
200 से कम	7	7
200 – 300	13	20
300 – 400	24	44
400 – 500	16	60
500 या उससे अधिक	10	70

M = \(\frac{n}{2}\) वाँ अवलोकन मूल्य = \(\frac{70}{2}\)
= 35 वाँ अवलोकन मूल्य ef की सारणी में देखने पर 35 के समक्ष M वर्ग 300-400 है ।
∴ M = L + \(\frac{n / 2-c f}{f}\) × c जहाँ L = 300, \(\frac{n}{2}\) = 35, cf = 20, f = 24, c = 100
= 300 + \(\frac{35-20}{24}\) × 100 = 300 + \(\frac{15 \times 100}{24}\) = 300 + \(\frac{1500}{24}\) = 300 + 62.5
∴ M = 362.5 युनिट
परिवार में उपयोग में लिए गए बिजली के युनिट की मध्यका 362.5 युनिट है ।

प्रश्न 2.
एक व्यापारी का सप्ताह के दौरान लाभ-हानि की निम्न सूचना पर से लाभ का बहुलक ज्ञात करो।

उत्तर :
वर्ग 2 – 4 के लिए महत्तम आवृत्ति 14 है इसलिए बहुलक वर्ग 2 – 4 है ।
अब L = 2, fm = 14, f₁ = 8, f₂ = 6, c = 2

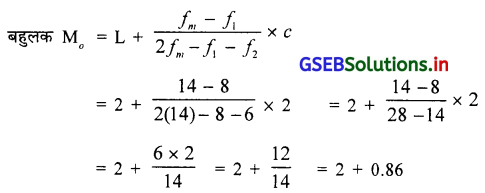
∴ M_O = 2.86 हजार रु. लाभ

प्रश्न 3.
एक करियाणा की दुकान में से प्रतिदिन बिक्री हुए गेहूँ की बोरी की संख्या निम्नानुसार है ।

बिक्री हुए बोरीओं की संख्या का Q₁ और D₄ ज्ञात करो ।
उत्तर :
आवृत्ति वितरण अनिवारक सतत है इसलिए सीमाबिंदु ज्ञात करके आवृत्ति वितरण निम्नानुसार लिखकर Q₁ और D₄ ज्ञात करेंगे ।

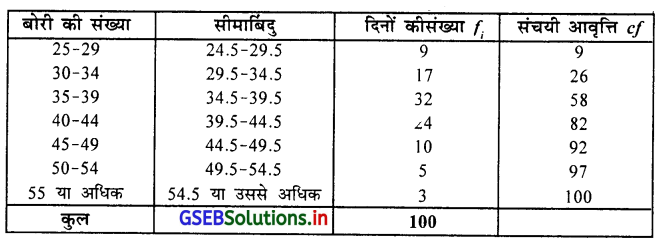
Q₁ = \(\frac{n}{4}\) वाँ अवलोकन मूल्य
= \(\frac{100}{4}\) = 25 वाँ अवलोकन मूल्य cf में देखने पर Q वर्ग 29.5 – 34.5
जहाँ L = 29.5, \(\frac{n}{4}\) = 25, cf = 9, f = 17, c = 5
Q₁ = L + \(\frac{\frac{n}{4}-c f}{f}\) × C = 29.5 + \(\frac{25-9}{17}\) × 5
= 29.5 + \(\frac{16 \times 5}{17}\) = 29.5 + \(\frac{80}{17}\) = 29.5 + 4.71
∴ Q₁ = 34.21 बोरी

⇒ D₄ = \(\frac{j n}{10}\) वाँ अवलोकन मूल्य
\(\frac{4 \times 100}{10}\) = 40 वाँ अवलोकन मूल्य को cf में देखने पर D₄ वर्ग = 34.5 – 39.5
जहाँ L = 34.5, \(\frac{j n}{10}\) = 40, cf = 26, f = 32, c = 5
∴ D₄ = L + \(\frac{\frac{j n}{10}-c f}{f}\) × c = 34.5 + \(\frac{40-26}{32}\) × 5
= 34.5 + \(\frac{70}{32}\) = 34.5 + 2.19 ∴ D₄ = 36.69 बोरी

प्रश्न 4.
एक कोलेज के विद्यार्थियों की ऊँचाई निम्न सारणी में प्रदर्शित है । विद्यार्थियों की ऊँचाई का माध्य ज्ञात कीजिए ।

उत्तर :
वर्ग की मध्यकिंमत ज्ञात करेंगे । उसके लिए सूत्र

का उपयोग करके प्राप्त करके वर्गलंबाई समान है, इसलिए d = \(\frac{\mathrm{X}-\mathrm{A}}{\mathrm{C}}\) d₁ = \(\frac{x-167.5}{5}\) लेकर निम्न सारणी बनेगी ।

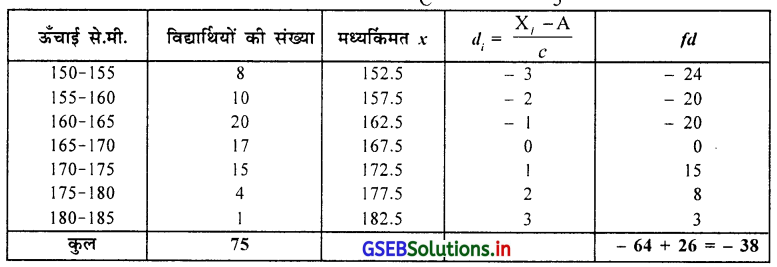
माध्य \(\bar{X}\) = A + \(\frac{\sum f d}{n}\) × c
= 167.5 + \(\frac{-38}{75}\) × 5
= 167.5 – \(\frac{190}{75}\) = 167.5 – 2.53
∴ \(\bar{X}\) = 164.97
कोलेज के विद्यार्थियों की ऊँचाई का माध्य 164.97 से.मी.

प्रश्न 5.
एक विस्तार के 130 व्यक्तियों की मासिक आय (हजार रु. में) निम्नानुसार है । आय की मध्यका ज्ञात कीजिए ।

उत्तर :
मध्यका (M) की गणना के लिए संचयी आवृत्ति की सारणी बनायेंगे ।

आय (हजार रु. में)	व्यक्तियों की संख्या f	संचयी आवृत्ति cf
4 से कम	6	6
4 – 8	14	20
8 – 12	31	51
12 – 20	35	86
20 – 28	28	114
28 – 36	16	130
कुल	130

M = \(\frac{n}{2}\) वाँ अवलोकन मूल्य
= \(\frac{130}{2}\) = 65 वाँ अवलोकन मूल्य cf की सारणी में देखने पर M वर्ग = 12 – 20 है ।
∴ M = L + \(\frac{n / 2-c f}{f}\) × c जहाँ L = 12, \(\frac{n}{2}\) = 65, cf = 51, f = 35, c = 8
= 12 + \(\frac{n}{2}\) × 8 = 12 + \(\frac{14 \times 8}{35}\)
= 12 + \(\frac{112}{35}\) = 12 + 3.2
∴ M = 15.2 हजार रु. आय

प्रश्न 6.
एक जिल्ला के 70 गाँव की जनसंख्या (हजार में) निम्नानुसार सारणी में है । उस पर से आलेख की विधि से जनसंख्या का भूयिष्ठक ज्ञात करो ।

उत्तर :

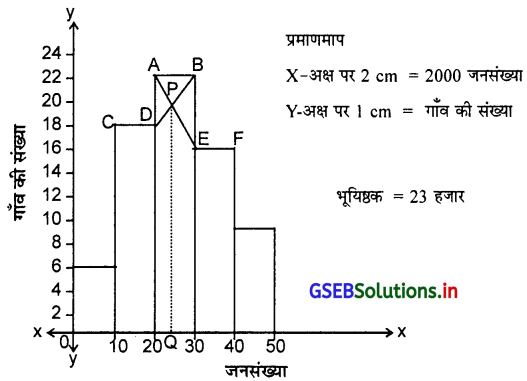
प्रश्न 7.
एक परीक्षा में 60 विद्यार्थियों के द्वारा प्राप्त नंबर का आवृत्ति वितरण निम्नानुसार है । विद्यार्थियों के गुण (नंबर) का माध्य ज्ञात करो ।

उत्तर :
आवृत्ति वितरण में वर्गलंबाई असमान है इसलिए प्रत्यक्ष विधि से माध्य ज्ञात करने के लिए निम्नानुसार सारणी बनेगी ।

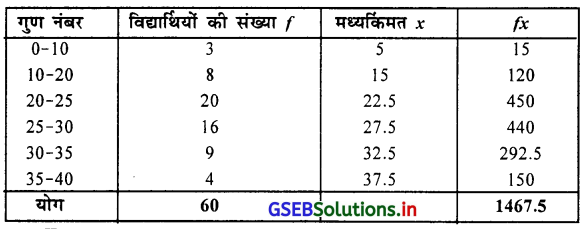
माध्य \(\overline{\mathrm{X}}=\frac{\sum f x}{n}=\frac{1467.5}{60}\) = 24.46 गुण (नंबर)
60 विद्यार्थियों द्वारा प्राप्त नंबर (गुण) का माध्य 24.46 गुण है ।

प्रश्न 8.
एक ओफिस के 50 कर्मचारियों द्वारा कम्प्यूटर के उपयोग के समय की जाँच की गई । उस सूचना पर से कम्प्यूटर के उपयोग का समय का चतुर्थक Q₁ और Q₃ ज्ञात कीजिए ।

उत्तर :
आवृत्ति वितरण निवारक सतत आवृत्ति वितरण है, वर्गलंबाई 0.5 है, संचयी आवृत्ति की सारणी निम्नानुसार प्राप्त करेंगे ।

समय (घण्टे)	कर्मचारियों की संख्या (f)	संचयी आवृत्ति cf
5 – 5.5	1	1
5.5 – 6	3	4
6 – 6.5	5	9
6.5 – 7	11	20
7 – 7.5	15	35
7.5 – 8	9	44
8 – 8.5	4	48
8.5 – 9	2	50
कुल	50

⇒ Q₁ = \(\frac{n}{4}\) वाँ अवलोकन मूल्य
= \(\frac{50}{4}\) = 12.5 वाँ अवलोकन मूल्य cf में देखने पर Q₁ वर्ग = 6.5 – 7
जहाँ L = 6.5 \(\frac{n}{4}\) = 12.5. cf = 9 , f = 11, c = 0.5

= 7.5 + \(\frac{1.25}{9}\) = 7.5 + 0.14
∴ Q₃ = 7.64 घण्टे
50 कर्मचारियों द्वारा उपयोग में लिए कम्प्यूटर का उपयोग का समय का Q₁ = 6.66 घण्टे और Q₃ = 7.64 घण्टे है ।

विभाग – F

निम्न के हल प्राप्त कीजिए ।

प्रश्न 1.
एक विद्यालय के 55 विद्यार्थियों के गुण (नंबर) की सूचना निम्नानुसार है ।

(1) यदि 30% विद्यार्थियों अनुत्तीर्ण हुए हो तो उत्तीर्ण होने के लिए आवश्यक गुण प्राप्त करो ।
(2) सबसे अधिक गुण (नंबर) प्राप्त करनेवाले 5% विद्यार्थियों को शिष्यवृत्ति देना हो तो उसमें न्यूनतम नंबर कितने होंगे?
उत्तर :
(1) यदि 30% विद्यार्थी अनुत्तीर्ण हो अर्थात् D₃ ज्ञात करेंगे ।
(2) सबसे अधिक गुण (नंबर) प्राप्त करनेवाले 5% विद्यार्थियों को शिष्यवृत्ति देना है अर्थात् P₉₅ ज्ञात करेंगे । संचयी आवृत्ति की सारणी निम्नानुसार प्राप्त करेंगे ।

गुण	विद्यार्थियों की संख्या (f)	संचयी आवृत्ति cf
0 – 10	4	4
10 – 20	7	11
20 – 30	11	22
30 – 40	14	36
40 – 50	9	45
50 – 60	7	52
60 – 70	3	55
कुल	55

(1) D₃ = \(\frac{j n}{10}\) वाँ अवलोकन मूल्य = \(\frac{3 \times 55}{10}\)
= \(\frac{165}{10}\) = 16.5 वाँ अवलोकन मूल्य cf की सारणी में देखने पर D₃ वर्ग = 20-30 है ।
जहाँ L = 20, \(\frac{j n}{10}\) = 16.5, cf = 11, f = 11, c = 10

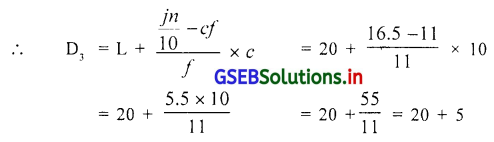
∴ D₃ = 25
अनुत्तीर्ण विद्यार्थियों के महत्तम गुण 25 होंगे इसलिए उत्तीर्ण होने के लिए 26 गुण आवश्यक है ।

(2) सबसे अधिक नंबर प्राप्त करनेवाले 5% विद्यार्थियों को शिष्यवृत्ति देना हो तो P₉₅ प्राप्त करेंगे ।
P₉₅ = \(\frac{j n}{10}\) वाँ अवलोकन मूल्य
\(\frac{95 \times 55}{100}\) = 52.25 वाँ अवलोकन मूल्य cf की सारणी में देखने पर P₉₅ वर्ग = 60-70 है ।

∴ P₉₅ = 60.83
सबसे अधिक नंबर प्राप्त करनेवाले 5% विद्यार्थियों के न्यूनतम नंबर (गुण) 60.83 = 61 गुण होंगे ।

प्रश्न 2.
दो ब्रान्ड के टायरों की उसके उम्र की तुलना करनी है । निम्न सूचना पर से माध्य के आधार पर कौन-सी ब्रान्ड का टायर अधिक श्रेष्ठ है ?

उत्तर :

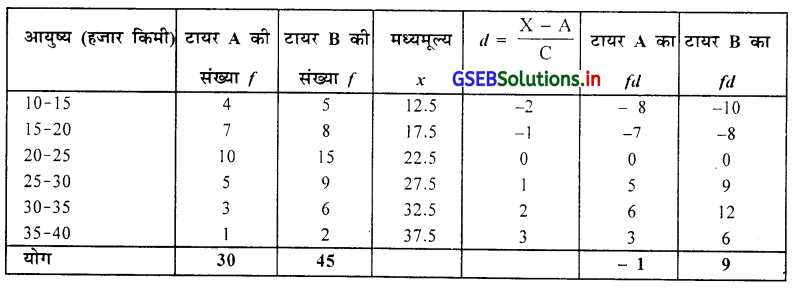
टायर A का माध्य
\(\bar{X}\) = A + \(\frac{\sum f d}{n}\) × C
= 22.5 + \(\frac{-1}{30}\) × 5
= 22.5 – \(\frac{5}{30}\)
= 22.5 – 0.17
∴ \(\bar{X}\) = 22.33 हजार कि.मी.

टायर B का माध्य
\(\bar{X}\) = A + \(\frac{\sum f d}{n}\) × C
= 22.5 + \(\frac{9}{45}\) × 5
= 22.5 + \(\frac{45}{45}\)
= 22.5 + 1
\(\bar{X}\) = 23.5 हजार कि.मी.
∴ टायर B का माध्य अधिक है इसलिए टायर B ब्रान्ड के टायर अच्छे है ।

प्रश्न 3.
एक कंपनी के भिन्न भिन्न दिन बिक्री मोटर की संख्या का आवृत्ति वितरण निम्नानुसार है । उस पर से बिक्री हुई मोटरों का भूयिष्ठक योग्य सूत्र से ज्ञात कीजिए ।

उत्तर :
आवृत्ति वितरण अनियमित प्रकार का है अर्थात् मिश्र प्रकार का है। इसलिए बहुलक ज्ञात करने के लिए अनुमानितता युक्त सूत्र M_O = 3M – 2\(\bar{X}\) का उपयोग करेंगे । इसके लिए माध्य (\(\bar{X}\)) और मध्यका M ज्ञात करेंगे । उसके लिए निम्नानुसार सारणी बनायेंगे ।

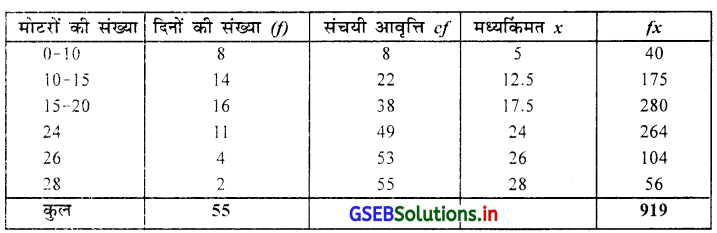
मध्य \(\bar{X}\) = \(\frac{\sum f x}{n}=\frac{919}{55}\)
∴ \(\bar{X}\) = 16.71 मोटर
भूयिष्ठक M_O
= 3M – 2\(\bar{X}\)
= 3 × 16.72 – 2 × 16.71
= 50.16 – 33.42 = 16.74 मोटर

मध्यका M = \(\frac{n}{2}\) वाँ अवलोकन मूल्य
= \(\frac{55}{2}\)
= 27.5 वाँ अवलोकन मूल्य of की सारणी में देखने
पर M वर्ग = 15 – 20
जहाँ L = 15, \(\frac{n}{2}\) = 27.5, cf = 22, f = 16, c = 5
M = L + \(\frac{n / 2-c f}{f}\) × c = 15 + \(\frac{27.5-22}{16}\) × 5
= 15 + \(\frac{5.5 \times 5}{16}\) = 15 + \(\frac{27.5}{16}\) = 15 + 1.72
∴ M = 16.72 माध्यिका M = 16.72 मोटर

प्रश्न 4.
एक राज्य के भिन्न भिन्न विस्तार में किसानों द्वारा प्राप्त गेहूँ का उत्पादन प्रति एकड़ निम्नानुसार है । उस पर से गेहूँ का प्रति एकड़ फसल का माध्य और मध्यका ज्ञात करो ।

उत्तर :
निवारक सतत आवृत्ति वितरण पर से माध्य और मध्यका प्राप्त करने के लिए निम्नानुसार सारणी बनायेंगे ।

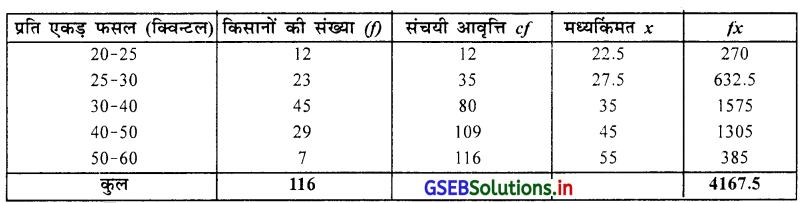
माध्य \(\overline{\mathrm{X}}=\frac{\sum f x}{n}=\frac{4167.5}{116}\)
∴ \(\overline{\mathrm{X}}\) = 35.93 क्विन्टल
मध्यका M = \(\frac{n}{2}\) वाँ अवलोकन मूल्य
= \(\frac{116}{2}\) = 58 वाँ अवलोकन मूल्य cf की सारणी में देखने पर M वर्ग = 30-40
जहाँ
L = 30, \(\frac{n}{2}\) = 58, cf = 35, f = 45, c = 10
M = L + \(\frac{n / 2-c f}{f}\) × c
= 30 + \(\frac{58-35}{45}\) × 10 = 30+ \(\frac{23 \times 10}{45}\) = 30 + \(\frac{230}{45}\) = 30 + 5.11
∴ M = 35.11 क्विन्टल
किसानों द्वारा प्राप्त गेहूँ का उत्पादन का माध्य (\(\bar{X}\)) = 35.93 क्विन्टल और मध्यका M = 35.11 क्विन्टल है ।

प्रश्न 5.
एक नाट्यगृह के 150 प्रेक्षकों की उम्र का आवृत्ति वितरण पर से प्रेक्षकों की उम्र का भूयिष्ठक आलेख की रीति से ज्ञात करो ।

उत्तर :

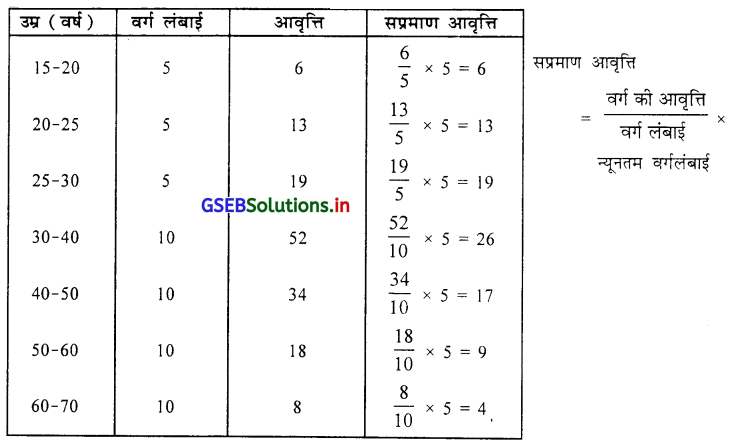
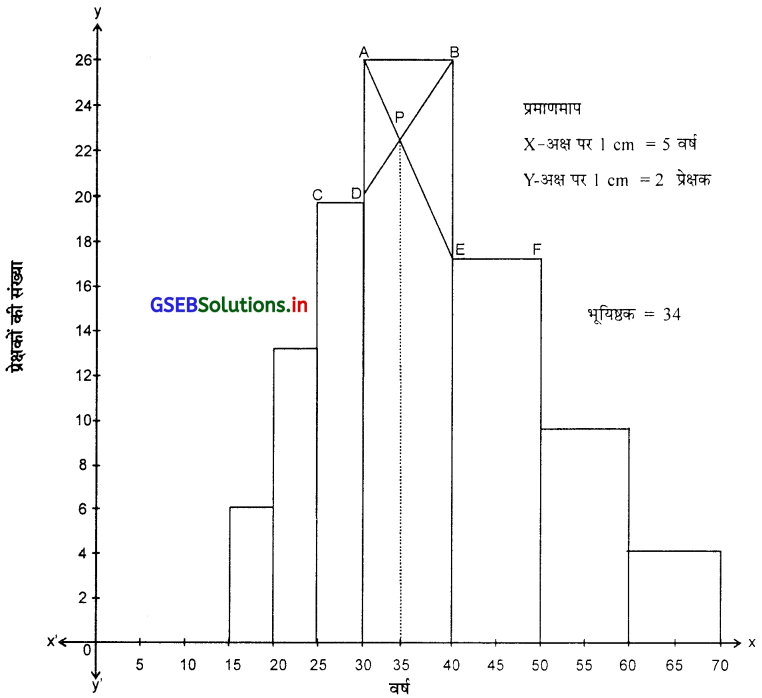
प्रश्न 6.
एक उत्पादक का प्रतिदिन उत्पादन का भूयिष्ठक 70 है । उत्पादक इकाई की डिजाईन में कुछ परिवर्तन करने के बाद लिए गए न्यादर्श की सूचना पर से उत्पादन का आवृत्ति वितरण निम्नानुसार प्राप्त हुआ है ।

उत्तर :
क्या उसके उत्पादन की संख्या के भूयिष्ठक में परिवर्तन हुआ है ?
वर्ग 70-74 की महत्तम आवृत्ति 10 है । इसलिए भूयिष्ठक वर्ग 70-74 है । वर्ग अनिवारक होने से वर्गसीमाबिंदु प्राप्त करेंगे। वर्ग के सीमाबिंदु 69.5 -74.5 लेंगे ।

बहुलक M_O = L + \(\frac{f_m-f_1}{2 f_m-f_1-f_2}\) × c
जहाँ L = 69.5, fm = 10, f₁ = 7, f₂ = 8, c = 5
M_O = 69.5 + \(\frac{10-7}{2(10)-7-8}\) × 5 = 69.5 + \(\frac{3 \times 5}{20-15}\)
= 69.5 + \(\frac{15}{5}\) = 69.5 + 3
∴ M_O = 72.5
इकाई डिझाईन में परिवर्तन करने से भूयिष्ठक के मूल्य में परिवर्तन हुआ है ।

प्रश्न 7.
एक दुकान में से प्रतिदिन बिक्री होते दो कंपनीओं के तेल के डिब्बे की बिक्री की निम्न सूचना है, 40 दिनों की बिक्री प्रदर्शित करता है ।

बिक्री की तुलना करने के लिए मध्यका का उपयोग किया जाए तो कौन-सी कंपनी की बिक्री अधिक है ऐसा कह सकते है ?
उत्तर :
दो कंपनी की तुलना करने के लिए मध्यका का उपयोग करना है । दोनों कंपनी के अनिवारक सतत आवृत्ति वितरण दिया है। सीमाबिंदु प्राप्त करके वर्ग निम्नानुसार लिखेंगे ।

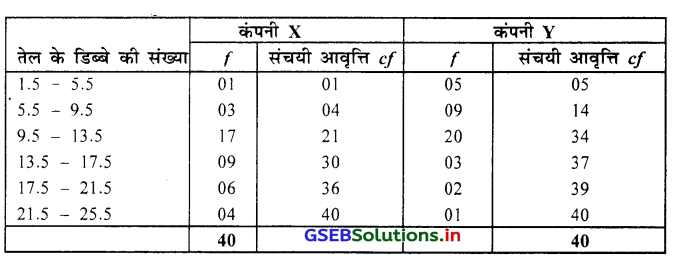
⇒ कंपनी X की मध्यका
M = \(\frac{n}{2}\) वाँ अवलोकन मूल्य
= \(\frac{40}{2}\) = 20 वाँ अवलोकन मूल्य cf की सारणी में देखने पर M वर्ग = 9.5 – 13.5 होगा ।
जहाँ L = 9.5, \(\frac{n}{2}\) = 20, cf = 4, f = 17, c = 4
∴ M = L + \(\frac{n / 2-c f}{f}\) × c
= 9.5 + \(\frac{20-4}{17}\) × 4 = 9.5 + \(\frac{64}{17}\) + 9.5 + 3.76
∴ M = 13.26 डिब्बे
⇒ कंपनी Y की मध्यका
M = \(\frac{n}{2}\) वाँ अवलोकन मूल्य
= \(\frac{40}{2}\) = 20 वाँ अवलोकन मूल्य cf की सारणी में देखने पर M वर्ग = 9.5 – 13.5 है ।
जहाँ L = 9.5, \(\frac{n}{2}\) = 20, cf = 14, f = 20, c = 4
∴ M = L + \(\frac{n / 2-c f}{f}\) × c
= 9.5 + \(\frac{20-14}{20}\) × 4 = 9.5 + \(\frac{24}{20}\) = 9.5 + 1.2
∴ M = 10.7 डिब्बे
कंपनी X का उत्पादन 13.26 डिब्बे और कंपनी Y का उत्पादन 10.7 डिब्बे का है ।
∴ कंपनी X का उत्पादन अधिक है ।

प्रश्न 8.
50 विवाहित पुरुषों की उसके विवाह के समय की उम्र का (पूरा वर्ष में) वितरण निम्नानुसार है । आलेख की विधि से उसकी विवाह के समय की उम्र का भूयिष्ठक ज्ञात करो ।

उत्तर :