GSEB Solutions Class 11 Statistics Chapter 8 फलन Ex 8

Gujarat Board Statistics Class 11 GSEB Solutions Chapter 8 फलन Ex 8 Textbook Exercise Questions and Answers.

Gujarat Board Textbook Solutions Class 11 Statistics Chapter 8 फलन Ex 8

विभाग – A

निम्न दिये विकल्प के लिए सहि विकल्प का चयन करो ।

प्रश्न 1.
निम्न दिये विधान में से कौन-सा विधान सत्य है ?
(A) f : {1, 2, 3, 4} → {3, 4, 5}, ‘प्रदेश समूच्य के मूल्य में 2 की वृद्धि करो’ यह नियम फलन नहि है ।
(B) f : A → B, A = {-2, -1, 0, 1, 2}, B = {0, 1, 2, 3, 4} के लिए f(x) = x² फलन नहि है ।
(C) g : P → Q; P = {-1, 0, 1} Q = {-\(\frac{1}{3}\), -1, 3}, g(x) = \(\frac{x+2}{x-2}\) है तो g को फलन कह सकते है ।
(D) g : {2, 3, 4, 5} → {-1, 0, 1} के लिए g(x) = 4x – 3 फलन है ।
उत्तर :
(A) f : {1, 2, 3, 4} → {3, 4, 5}, ‘प्रदेश समूच्य के मूल्य में 2 की वृद्धि करो’ यह नियम फलन नहि है ।

प्रश्न 2.
विधेय f : A → B के लिए विस्तार के लिए निम्न में से कौन-सा विधान सत्य है ?
(A) f(A) = {f(x) / x ∈ A
(B) सहप्रदेश गण का उपगण या सहप्रदेश स्वयं न हो ।
(C) प्रदेश उसका विस्तार होता है ।
(D) f(A) = {f(x) / x ∈ B}
उत्तर :
(A) f(A) = {f(x) / x ∈ A

प्रश्न 3.
g : x → y, x = {-1, 0} y = {2, 4}, g (x) = 4 – 2x इस पर से बताइए कि निम्न में से कौन-सा विधान सत्य है ?
(A) g को फलन कहा जाता है ।
(B) g को फलन नहि कह सकते ।
(C) x को फलन नहि कह सकते ।
(D) y को फलन कह सकते है ।
उत्तर :
(B) g को फलन नहि कह सकते ।

प्रश्न 4.
f : A → B के लिए प्रदेश गण A की कोई दो भिन्न किंमत के लिए विधेयात्मक किंमत समान मिले तो उस संबंध को क्या कहते है ?
(A) एक-एक फलन
(B) अनेक-एक फलन
(C) एक-अनेक फलन
(D) अनेक-अनेक फलन
उत्तर :
(B) अनेक-एक फलन

प्रश्न 5.
f : A → B के लिए समूच्य A की प्रत्येक किमत के लिए समूच्य B में सिर्फ एक ही प्रतिबिंब मिलता हो उसे कौन से प्रकार का फलन कहते है ?
(A) फलन नहि कहा जाता
(B) एक-एक फलन
(C) अचल फलन कहते है
(D) अनेक-एक फलन
उत्तर :
(C) अचल फलन कहते है

प्रश्न 6.
एक-एक विधेय के लिए निम्न में से कौन-सा विधान सत्य है ?
(A) प्रदेश की सिर्फ दो किंमत के लिए प्रतिबिंब भिन्न होना चाहिए ।
(B) प्रदेश की कोई दो किंमतों के लिए प्रतिबिंब समान होना चाहिए ।
(C) प्रदेश की कोई दो भिन्न किंमतों के लिए प्रतिबिंब भिन्न होना चाहिए ।
(D) प्रदेश की प्रत्येक किंमतों के लिए प्रतिबिंब समान होना चाहिए ।
उत्तर :
(C) प्रदेश की कोई दो भिन्न किंमतों के लिए प्रतिबिंब भिन्न होना चाहिए ।

प्रश्न 7.
f : z – {0} → N और f (x) = x², x ∈ z – {0} यह कौन से प्रकार का फलन है ?
(A) एक-एक फलन है।
(B) अनेक-एक फलन है ।
(C) अचल फलन है।
(D) f(x) यह फलन नहि है।
उत्तर :
(B) अनेक-एक फलन है ।

प्रश्न 8.
दो भिन्न फलन समान हो उसके लिए निम्न में से कौन-सी शर्त पर्याप्त है ?
(A) दोनों फलनों का प्रदेश समान होना चाहिए ।
(B) दोनों फलनों का विस्तार समान होना चाहिए ।
(C) (A) और (B)
(D) (A) अथवा (B)
उत्तर :
(C) (A) और (B)

विभाग – B

निम्न प्रश्नों के उत्तर एक वाक्य में लिखिए ।

प्रश्न 1.
फलन पारिभाषिक होने के लिए आवश्यक शर्त बताइए ।
उत्तर :
दो अरिक्त समूच्य के घटकों के बीच के अनन्य संबंध को विधेय कहते है । अर्थात् A और B के घटक अरिक्त नहि होना चाहिए ।

प्रश्न 2.
f: A → B, A = {-3, -1, 1, 3}, B = {1, 0, 9}, f(x) = x² विधेय है ।
उत्तर :
गण A = {-3, -1, 1, 3} के प्रत्येक घटक के लिए B का घटक अनन्य रीति से प्राप्त होता है अर्थात् A का प्रत्येक घटक
गण B के अनन्य घटक के साथ नियम x2 से जुड़ा है इसलिए f(x) = x² फलन है।

प्रश्न 3.
g : N → N प्रदेश गण के प्रत्येक घटक में से 2 घटाया जाय तो यह नियम को फलन कह सकते है ?
उत्तर :
प्रदेश गण के प्रत्येक घटक में से 2 घटाया जाय तो g : N → N दिया है इसलिए प्राकृतिक समूच्य बताता नहि है इसलिए फलन नहि है ।

प्रश्न 4.
एक-एक फलन की सांकेतिक परिभाषा दीजिए ।
उत्तर :
विधेय f : A → B प्रदेश गण A के कोई भी दो भिन्न घटकों के लिए सहप्रदेश के गण में प्राप्त प्रतिबिंबों के विधेयात्मक किंमत भिन्न हो तो उस विधेय f को एक-एक विधेय कहते है ।
f : A → B के लिए यदि a₁ ≠ a₂ तथा a₁, a₂ ∈ A के लिए यदि f(a₁) ≠ f(a₂) होता हो तो विधेय f को एक-एक विधेय कहते है ।

प्रश्न 5.
अनेक-एक फलन की सांकेतिक परिभाषा दीजिए ।
उत्तर :
मानाकि f : A → B, प्रदेश गण A के कोई भी दो घटक के लिए सहप्रदेश गण में प्राप्त प्रतिबिंबों या विधेयात्मक किंमत समान हो तो उस विधेय f को अनेक-एक विधेय कहते है ।
f : A → B के लिए यदि a₁ ≠ a₂, a₁, a₂, ∈ A के लिए यदि f(a₁) = f(a₂) बनता हो तो विधेय f को अनेक-एक विधेय कहते है ।

प्रश्न 6.
अचल फलन की सांकेतिक परिभाषा दीजिए।
उत्तर :
मानाकि f : A → B है यदि प्रदेश गण A के प्रत्येक घटक के लिए सहप्रदेश गण B में सिर्फ एक ही प्रतिबिंब प्राप्त होता हो तो फलन f को अचल फलन कहते है ।

प्रश्न 7.
f : {1, 2, 3} → N, g : {2, 3, 4} → N, f(x) = 2x + 1 और g(x) = x – 1 f और g समान फलन है ? क्यों ?
उत्तर :
f(x) = 2x + 1
फलन f का प्रतिबिंब f(1) = 2(1) + 1
= 2 + 1
= 3

f(2) = 2(2) + 1
= 4 + 1
= 5

f(3) = 2(3) + 1
= 6 + 1
= 7

फलन g(x) = x – 1 के प्रतिबिंब

g(2) = 2 – 1
= 1

g(3) = 3 – 1
= 2

g(4) = 4 – 1
= 3

यहाँ f(x) ≠ g(x) है इसलिए समान फलन नहि है । क्योंकि दोनों फलन के प्रदेश समूच्य भिन्न है ।

प्रश्न 8.
विधेय f : z → N f(t) = t² + 1 t ∈ z है, तो f का प्रकार निश्चित करो ।
उत्तर :
प्रदेश गण D_f = Z = {….-2, -1, 0, 1, 2}
सहप्रदेश B = N = {1, 2, 3…..}
f(t) = t² + 1
f(-2) = (-2)² + 1
= 4 + 1 = 5

f(-1) = (-1)² + 1
= 1 + 1 = 2

f(0) = 0 + 1
= 1

f(1) = 1 + 1
= 2

f(2) = 2² + 1
= 5
दो भिन्न किंमत (-2, 2) और (-1, 1) के प्रतिबिंब समान मिलते है इसलिए f अनेक-एक फलन है ।

प्रश्न 9.
फलन f : N → Nf(t) = t²+ 1 t ∈ N है, तो f का प्रकार निश्चित करो ।
उत्तर :
प्रदेश गण D_f = N = {1, 2, 3….}
सह प्रदेश B = N = {1, 2, 3….}
f(t) = t² + 1 में t = 1, 2, 3 रखने पर
f(1) = 1² + 1
= 2

f(2) = 2² + 1
= 5

f(3) = 3² + 1
= 10

t = 1, 2, 3 के प्रतिबिंब 2, 5, 10 प्राप्त होते है। प्रदेश की दो भिन्न किंमत के लिए सहप्रदेश के भिन्न प्रतिबिंब प्राप्त होते है। इस लिए f एक-एक फलन है ।

प्रश्न 10.
वास्तविक चल का फलन को पारिभाषित करो ।
उत्तर :
यदि फलन का प्रदेश और उसका विस्तार वास्तविक संख्या R पर पारिभाषित हो तो उसे वास्तविक फलन कहते है ।

विभाग – C

निम्न प्रश्नों के उत्तर दीजिए ।

प्रश्न 1.
फलन की परिभाषा दीजिए ।
उत्तर :
यदि समूच्य A और B रिक्त न हो ऐसे दो भिन्न समूच्य हो और समुच्य A.का प्रत्येक घटक समूच्य B के किसी एक अनन्य घटक के साथ किसी नियम, संबंध या संगतता से जुड़ा हुआ हो तो ऐसे नियम, संबंध या संगतता को गण A से समूच्य B पर का फलन (Function) कहते है । उसे संकेत में f.g.h.k इत्यादि से दर्शाया जाता है ।

प्रश्न 2.
फलन के प्रदेश और सहप्रदेश की परिभाषा दीजिए।
उत्तर :
फलन दो भिन्न अरिक्त समूच्यों के घटकों विचल अनन्य संबंध है । समूच्य A के घटक के लिए समूच्य B में अनन्य घटक के प्रतिबिंब प्राप्त किया जाता है यहाँ समूच्य A को प्रदेश और समूच्य B को सहप्रदेश कहते है ।

प्रश्न 3.
फलन के विस्तार पारिभाषित करो।
उत्तर :
प्रदेश समूच्य के घटक के लिए फलन की प्रतिबिंब किंमत या विधेयात्मक किंमत प्राप्त की जाती है । उस किंमत के समूच्यों को फलन का विस्तार कहते है । उसे R_f से दर्शाया जाता है ।

प्रश्न 4.
विधेय g : A → N, A = {x /x ∈ N, 1 < x ≤ 4} g(x) = x + 1 का विस्तार लिखिए। . . .
उत्तर :
प्रदेश A = D_f = {2, 3, 4}
g(x) = x + 1 के लिए
R_f प्राप्त करेंगे ।
x = 2 के लिए g(2) = 2 + 1 = 3
x = 3 के लिए g(3) = 3 + 1 = 4
x = 4 के लिए 8(4) = 4 + 1 = 5
विस्तार R_f = {3, 4, 5}

प्रश्न 5.
K: x → Y के लिए x = {t ∈ Z; – 3 ≤ t ≤ 3}, y = {a / a ∈ N, 1 ≤ a ≤ 20}, k(t) = t² + 2 हो, तो k का प्रकार बताइए ।
उत्तर :
यहा x = { t ∈ z} है इसलिए
प्रदेश गण D_f = x = t = {-3, -2, -1, 0, 1, 2, 3}
सहप्रदेश y = {a / a ∈ N 1 ≤ a ≤ 20}
K(t) = t² + 2 के लिए t = -3, -2, -1, 0, 1, 2, 3 रखने पर

K(-3) = (-3)² + 2
= 9 + 1
= 11

K(3) = (3)² + 2
= 9 + 2
= 11

K(-2) = (-2)² + 2
= 4 + 2
= 6

K(2) = (2)² + 2
= 4 + 2
= 6

K(-1) = (-1)² + 2
= 1 + 2
= 3

K(1) = (1)² + 2
= 1 + 2
= 3

K(0) = 0² + 2
= 2

t = -3, -2, -1, 0, 1, 2, 3 के लिए विधेय का मूल्य 11, 6, 3, 0, 3, 6, 11 प्राप्त होते है ।
इसलिए प्रदेश समूच्य की दो भिन्न किंमत {-3, 3}, {-2, 2} और (-1, 1) के लिए प्रतिबिंब समान प्राप्त है इसलिए अनेक एक फलन है ।

प्रश्न 6.
h : A → B के लिए A = {1, 2, 3}, B = {3, 4, 5, 6, 7, 8}, h(x) = x + 5 के लिए विधेय h का प्रकार बताइए ।
उत्तर :
प्रदेश समूच्य D_f = A = {1, 2, 3}
सहप्रदेश समूच्य B = {3, 4, 5, 6, 7, 8}
h(x) = x + 5 में x = 1, 2, 3 रखने पर
h(1) = 1 + 5 = 6 h(2) = 2 + 5 = 7 f(3) = 3 + 5 = 8
उसके प्रतिबिंब 6, 7, 8 प्राप्त होता है ।
प्रदेश की दो भिन्न किंमत के लिए सहप्रदेश में भिन्न प्रतिबिंब प्राप्त होता है इसलिए दिया विधेय h एक-एक फलन है ।

प्रश्न 7.
यदि P : A → B, P(x) = 2x – 3 और R_f = {-2, -1, 0} हो तो फलन का प्रदेश समुच्य प्राप्त करो ।
उत्तर :
प्रदेश समूच्य A P(x) = 2x – 3 और विस्तार R_f = {-2, -1, 0} दिया है ।
∴ -2 = 2(x) – 3
-2 = 2x – 3
– 2 + 3 = 2x
\(\frac{1}{2}\) = x
∴ x = \(\frac{1}{2}\)

– 1 = 2(x) (-3)
– 1 = 2x – 3
-1 + 3 = 2x
\(\frac{2}{2}\) = x
x = 1

0 = 2x – 3
0 + 3 = 2x
\(\frac{3}{2}\) = x
∴ x = \(\frac{3}{2}\)

प्रदेश समूच्य A = {\(\frac{1}{2}\), 1, \(\frac{3}{2}\)}

प्रश्न 8.
यदि f : R→ R – {-1, 1}, f(x) = 1 – \(\frac{1}{1-\mathrm{x}^2}\), x ∈ R – {-1, 1} हो, तो f(2) – (-2) का मूल्य ज्ञात करो।
उत्तर :
वास्तविक समूच्य दिया है और x ∈ R – {-1, 1} हो, तो f(x) = 1 – \(\frac{1}{1-\mathrm{x}^2}\) में f(2) रखने पर

f(2) = 1 – \(\frac{1}{1-(2)^2}\) = 1 – \(\frac{1}{1-4}\) = 1 – \(\frac{1}{-3}\)
= \(\frac{3+1}{3}=\frac{4}{3}\)

f(-2)
= 1 – \(\frac{1}{1-(-2)^2}\) = 1 – \(\frac{1}{1-4}\) = 1 – \(\frac{1}{-3}=\frac{3+1}{3}=\frac{4}{3}\)

∴ f(2) – f(-2)
\(\frac{4}{3}\) – \(\frac{4}{3}\)
∴ = 0

प्रश्न 9.
यदि f : N → N, f(x) = \(\frac{x-3}{x+4}\) का प्रदेश समूच्य (0, 3, 6) हो, तो उसका विस्तार ज्ञात करो ।
उत्तर :
N → N है इसलिए प्रदेश समूच्य A = {1, 2, 3 …..} सहप्रदेश B = {1, 2, 3….} होना चाहिए ।
∴ R_f ज्ञात करने के लिए प्रदेश समूच्य 0, 3, 6 के लिए विस्तार ज्ञात करने हेतु
f(x) = \(\frac{x-3}{x+4}\) में x = 0, 3, 6 रखने पर
f(0) = \(\frac{0-3}{0+4}\)
= \(\frac{-3}{4}\)
f(0) = \(\frac{-3}{4}\)

f(3) = \(\frac{3-3}{3+4}\)
= \(\frac{0}{7}\)
f(3) = 0

f(6) = \(\frac{6-3}{6+4}\)
\(\frac{3}{10}\)
f(6) = \(\frac{3}{10}\)
R_{f =} {\(\frac{-3}{4}\), 0, \(\frac{3}{10}\)}

प्रश्न 10.
यदि वास्तविक फलन f(x) = \(\frac{\mathrm{x}^2(\mathrm{x}+1)^2}{4}\) हो, तो f(3) – f(2) का मूल्य ज्ञात करो ।
उत्तर :
f(3) – f(2) ज्ञात करने के लिए x = 3 रखने पर

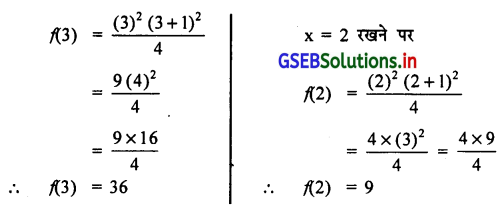
∴ f(3) – f(2)
36 – 9
∴ 27

प्रश्न 11.
यदि f : R → R और (x) = x² + 2x – 1 हो, तो फलन का प्रकार बताइए ।
उत्तर :
यहाँ f : R → R दिया है इसलिए प्रदेश समूच्य A = {…-3, -2, -1, 0, 1, 2, 3} रखने पर
f(-3) = (-3)² + 2 (-3) -1
= 9 – 6 – 1
= 2

f(-2) = (-2)² + 2(-2) -1
= 4 – 4 – 1
= -1

f(-1) = (-1)² + 2(-1) – 1
= 1 – 2 – 1
= -2

f(0) = (0)² + 2(0) – 1
= -1

f(1) = (1)² + 2(1) – 1
= 1 + 2 – 1
= 2

f(2) = (2)² + 2(2) – 1
= 4 + 4 – 1
= 7

f(3) = (3)² + 2 (3) – 1
= 9 + 6 – 1
= 14

(-3, 1), (-2, 0) का विस्तार 2 और (-1) प्राप्त होता है इसलिए अनेक-एक फलन है ।

प्रश्न 12.
वास्तविक विधेय f(x) = \(\frac{2 x-4}{x+7}\) के लिए x की कौन-सी किंमत के लिए प्रतिबिंब शून्य होगा ?
उत्तर :
f(x) = \(\frac{2 x-4}{x+7}\) में x = 2 रखने पर
f(2) = \(\frac{2(2)-4}{2+7}\)
∴ \(\frac{4-4}{9}=\frac{0}{9}\) = 9
∴ x = 2 के लिए प्रतिबिंब शून्य होगा ।

प्रश्न 13.
f : z – {2} → z, f(x) = \(\frac{x^2+x-6}{x-2}\) हो, तो फलन का प्रकार बताइए ।
उत्तर :
f : z – [2] → z दिया है इसलिए वास्तविक फलन है जिस में 2 के अलावा वास्तविक संख्या प्रदेश समूच्य A = {-3,
-2, -1, 0, 1, 3} का उपयोग करके प्रकार की जाँच करेंगे ।
f(x) = \(\frac{x^2+x-6}{x-2}\) में x = – 3, – 2, – 1, 0, 1, 3 रखने पर


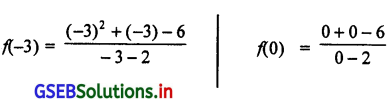
यहाँ प्रदेश समूच्य के दो भिन्न किंमतों के लिए सहप्रदेश के प्रतिबिंब भिन्न प्राप्त होते है इसलिए दिया गया विधेय एक-एक फलन है ।

प्रश्न 14.
वास्तविक विधेय f(x) = 6x³ – 5^x + 15 के लिए f(0) का मूल्य ज्ञात करो ।
उत्तर :
विधेय वास्तविक है इसलिए f(0) का मूल्य f(x) = 6x³ – 5^x + 15 में x = 0 रखने पर
∴ f(o) = 6(0)³ – 5⁰ + 15
= 6 × 0 – 1 + 15
= 0 – 1 + 15
∴ f(o) = 14

प्रश्न 15.
वास्तविक विधेय f(x) = x³ – 2x + \(\frac{1}{\mathrm{x}}\) के लिए f(3) + f(-3) की किंमत ज्ञात करो ।
उत्तर :
वास्तविक विधेय है । f(3) + f(-3) ज्ञात करने के लिए
f(x) = x³ – 2x + \(\frac{1}{\mathrm{x}}\) में x = 3 रखने पर

f(3) = (3)³ – 2(3) + \(\frac{1}{3}\)
= 27 – 6 + \(\frac{1}{3}\)
= 21 + \(\frac{1}{3}\)
= \(\frac{63+1}{3}\)
∴ f(3) = \(\frac{64}{3}\)

f(x) = x³ – 2x + \(\frac{1}{\mathrm{x}}\) में x = -3 रखने पर
f(-3) = (-3)³ – 2 (-3) + \(\frac{1}{-3}\)
= -27 + 6 + \(\frac{1}{-3}\)
= -21 + \(\frac{1}{-3}\)
= \(\frac{-21(-3)-1}{+3}\)
∴ f(-3) = \(\frac{-64}{3}\)
अब f(3) + f(-3) में f(3) = \(\frac{64}{3}\) और f(-3) = \(\frac{-64}{3}\) रखने पर
∴= \(\frac{64}{3}+\frac{-64}{3}\)
= \(\frac{64}{3}-\frac{64}{3}\)
∴ = 0

विभाग – D

निम्न के हल प्राप्त करो ।

प्रश्न 1.
f : A → B, A = {10, 20, 30}, B = {18, 48, 98, 128, 148}, f(x) = 5x – 2 के लिए प्रदेश, सहप्रदेश और विस्तार
प्राप्त करो ।
उत्तर :
प्रदेश A = D_f = {10, 20, 30}
सहप्रदेश B = {18, 48, 98, 128, 148}
f(x) = 5x – 2 है इसलिए प्रत्येक x ∈ A के लिए f(x) प्राप्त करेंगे ।
x = 10 के लिए f(10) = 5(10) – 2 = 50 – 2 = 48
x = 20 के लिए f(20) = 5(20)- 2 = 100 – 2 = 98
x = 30 के लिए f(30) = 5(30) – 2 = 150 – 2 = 148
∴ विस्तार R_f = {f(10), (20), f(30)} = {48, 98, 148}

प्रश्न 2.
f : P → Q, P = {-\(\frac{1}{2}\), 1, \(\frac{1}{2}\), \(\frac{3}{2}\)}, Q = {-\(\frac{1}{5}\), 1, \(\frac{1}{3}\), 3}, f(x) = \(\frac{x}{2-x}\) के लिए प्रदेश, सहप्रदेश और विस्तार प्राप्त करो ।
उत्तर :
प्रदेश P = D_f = {-\(\frac{1}{2}\), 1, \(\frac{1}{2}\), \(\frac{3}{2}\)}
सहप्रदेश Q = {-\(\frac{1}{5}\), 1, \(\frac{1}{3}\), 3}
f(x) = \(\frac{x}{2-x}\) के लिए x ∈ p f(x) प्राप्त करेंगे ।

प्रश्न 3.
यदि R → R, f(x) = \(\frac{1}{x}\)(1 + \(\frac{1}{x}\)) – 1 हो, तो f(-1), (-2) और f(\(\frac{1}{2}\)) की किंमत प्राप्त करो ।
उत्तर :
R → R वास्तविक समूच्य है ।

प्रश्न  4.
यदि विधेय f : A → B, f(x) = 4x – 3 के लिए R_f = {9, 13, 17, 25} हो, तो D, प्राप्त करो ।
उत्तर :
यहाँ f : A → B दिया है और उसका विस्तार R_f = {9, 13, 17, 25} दिया है । उस पर से प्रदेश A प्राप्त करने के लिए f(x) = 4x – 3 में विस्तार मूल्य 9, 13, 17, 25 रखने पर

f(x) = 4x – 3
∴ 9 = 4x – 3
∴ 9 + 3 = 4x
∴ = \(\frac{12}{4}\) = x
∴ x = 3

f(x) = 13
∴ 13 = 4x – 3
13 + 3 = 4x
∴ 16 = 4x
∴ x = 4

f(x) = 17 रखने पर
17 = 4x – 3
17 + 3 = 4x
∴ 4x = 20
∴ x = \(\frac{20}{4}\)
∴ x = 5

f(x) = 25 रखने पर
25 = 4x – 3
∴ 25 + 3 = 4x
∴ 4x = 28
∴ x = \(\frac{28}{4}\)
∴ x = 7
R_f = {9, 13, 17, 25} के लिए प्रदेश D_f = {3, 4, 5, 7} प्राप्त होगा ।

प्रश्न 5.
यदि वास्तविक फलन f(x) = 2x² – 5x + 4 हो, तो x की कौन-सी किंमत के लिए f(3x) – 3f(x) + 5 = 0 होगा?
उत्तर :
f(x) = 2x² – 5x + 4
∴ f(3x) = 2(3x)² – 5(3x) + 4
= 2 × 9x² – 15x + 4
∴ f(3x) = 18x² – 15x + 4

3f(x) = 3(2x)² – 5(3x) + 4 × 3
∴ = 6x² – 15x + 12
∴ 3f(x) = 6x² – 15x + 12

f(3x) – 3f(x) + 5 = 0 में (3x) और 3f(x) के मान रखने पर
∴ 18x² – 15x + 4 – (6x² – 15x + 12) + 5 = 0
∴ 18x² – 15x + 4 – 6x² + 15x – 12 + 5 = 0
∴ 12x² – 3 = 0
∴ 3(4x² – 1) = 0
∴ 4x² – 1
∴ x² = \(\frac{1}{4}\)
∴ x = ± \(\frac{1}{2}\)

प्रश्न 6.
यदि f : A → M, A = {x/x ∈ N; 1 ≤ x < 5} और M = {x/x ∈ N; 1 ≤ x ≤ 20} और f(x) = x² + 1 हो, तो फलन f का विस्तार ज्ञात करो ।
उत्तर :
f : A → M, A = {x/x ∈ N, 1 ≤ x < 5} और M = {x/x ∈ N, 1 ≤ x ≤ 20} दिया है ।
∴ प्रदेश A = D_f = {x/x ∈ N, 1 ≤ x ≤ 5} |
∴ सहप्रदेश M = {x/x ∈ N, 1 ≤ x ≤ 20}
f(x) = x² + 1 है इसलिए f(x) प्राप्त करेंगे ।
x = 1, 2, 3, 4 रखने पर
x = 1 के लिए f(1) = (1)² + 1 = 1 + 1 = 2
x = 2 के लिए f(2) = (2)² + 1 = 4 + 1 = 5
x = 3 के लिए f(3) = (3)² + 1 = 9 + 1 = 10
x = 4 के लिए f(4) = (4)² + 1 = 16 + 1 = 17
∴ विस्तार D_f = {(1), f(2), f(3), f(4)} = {2, 5, 10, 17} प्राप्त होगा ।

प्रश्न 7.
यदि f(x) = \(\frac{x^2-4}{x-2}\) जहाँ x ∈ z – {2} हो, तो f(0) + f(1) – f(-2) का मूल्य ज्ञात करो ।
उत्तर :
यहाँ x ∈ z – {2} दिया है जो वास्तविक समूच्य है ।
∴ f(x) = \(\frac{x^2-4}{x-2}\) के लिए f(0), f(1), f(-2) का मूल्य प्राप्त करेंगे ।
x = 0 के लिए f(0) = \(\frac{(0)^2-4}{0-2}=\frac{-4}{-2}\) = 2
x = 1 लिए f(1) = \(\frac{(1)^2-4}{1-2}=\frac{1-4}{-1}=\frac{-3}{-1}\) = 3
x = (-2) के लिए f(-2) = \(\frac{(-2)^2-4}{-2-2}=\frac{4-4}{-4}=\frac{0}{-4}\) = 0
अब f(0) + f(1) – f(-2) में f(0) = 2, f(1) = 3, f(-2) = 0 रखने पर
∴ = 2 + 3 – 0 = 5 – 0
∴ = 5

प्रश्न 8.
विधेय f(x) = \(\sqrt{x^2-16}\) का प्रदेश {4, 5} हो, तो उसका विस्तार ज्ञात करो ।
उत्तर :
यहाँ प्रदेश A = {4, 5} दिया है । D_f ज्ञात करने के लिए x = 4 और x = 5 रखने पर
x = 4 रखने पर f(4) = \(\sqrt{(4)^2-16}\)
∴ f(4) = \(\sqrt{16-16}=\sqrt{0}\)
f(4) = 0

x = 5 रखने पर f(5) = \(\sqrt{(5)^2-16}\)
∴ f(5) = \(\sqrt{25-16}=\sqrt{9}\)
∴ f(5) = 3
∴ विस्तार D_f = {f(4), f(5)} = {0, 3} प्राप्त होगा ।

प्रश्न 9.
यदि f(x) = x² और g(x) = 5x – 6 जहाँ x ∈ {2, 3, 4} है तो दोनों फलनों की समानता की जाँच करो।
उत्तर :
यहाँ दोनों विधेय के प्रदेश समूच्य समान है । A = {2, 3, 4} f(x) = x² और g(x)= 5x – 6 में x = 2, 3, 4 रखने पर x = 2 के लिए f(2) = (2)² = 4 और g(2) = 5 x 2 – 6 = 10 – 6 = 4
x = 3 के लिए f(3) = (3)² = 9 और g(3) = 5 × 3 – 6 = 15 – 6 = 9
x = 4 के लिए f(4) = (4)² = 16 और g(4) = 5 × 4 – 6 = 20 – 6 = 14
यहाँ f(4) g(4) है इसलिए f(x) और g(x) समान विधेय नहि है ।

प्रश्न 10.
यदि k : R → R और k(x) = x² + 3x – 12 हो, तो फलन k का प्रकार बताइए ।
उत्तर :
यहा k : R → R दिया है इसलिए प्रदेश गण
A = {… – 3, -2, -1, 0, 1, 2, 3…} और सहप्रदेश गण
B = {…. -3, -2, -1, 0, 1, 2, 3…} होगा
k(x) = x² + 3x – 12 के लिए x = -3, -2, -1, 0, 1, 2, 3 रखने पर

x = -3 के लिए f-3) = (-3)² + 3(-3) – 12 = 9 – 9 – 12 = – 12
x = -2 के लिए f(-2) = (-2)² + 3(-2) – 12 = 4 – 6 – 12 = – 14
x = -1 के लिए f(-1) = (-1)² + 3 (-1) – 12 = 1 – 3 – 12 = – 14
x = 0 के लिए f(0) = (0)² + 3 (0) – 12 = 0 + 0 – 12 = – 12
x = 1 के लिए f(1) = (1)² + 3 (1) – 12 = 1 + 3 – 12 = – 8
x = 2 के लिए f(2) = (2)² + 3 (2) – 12 = 4 + 6 – 12 = – 2
x = 3 के लिए f(3) = (3)² + 3 (2) – 12 = 9 + 6 – 12 = 3
k(-3, 0) और k(-2 और -1) के प्रतिबिंब (-12 और -14) समान प्राप्त होता है इसलिए फलन K अनेक-एक प्रकार का फलन है ।

प्रश्न 11.
यदि f(x) = x(3x – 2) और g(x) = x³ और x ∈ {0, 1, 2} हो, तो सिद्ध करो कि । और g समान विधेय है।
उत्तर :
यहा x ∈ {0, 1, 2} दिया है इसलिए f(x) और g(x) दोनों का प्रदेश समूच्य 0, 1, 2 समान होगा ।
अब f(x) = x(3x – 2) और g(x) = x³ में x = 0, 1, 2 रखने पर

x = 0 के लिए f(0) = 0(3(0) – 2)
= 0 (0 – 2)
∴ f(0) = (0)

x = 0 के लिए g(0) = (0)³
∴ g(0) = 0

x = 1 के लिए f(1) = 1(3(1) – 2) और g(1) = (1)³
= 1 (3 – 2) ∴ g(1) = 1
= 1 (1)
∴ f(1) = 1

x = 2 के लिए f(2) = 2(3(2) – 2) और g(2) = (2)³
= 2 (6 – 2) ∴ g(2) = 8
= 2 × 4
∴ f(2) = 8

यहाँ f(0), f(1), f(2) के लिए g(0), g(1), g(2) का मूल्य समान प्राप्त होता है । समान फलन है ।
∴ f और g समान फलन है ।

प्रश्न 12.
यदि f(x) = \(\frac{2 x+3}{5 x+2}\), x ∈ R हो, तो f(2) f(\(\frac {1}{2}\)) का मूल्य ज्ञात करो ।
उत्तर :
x ∈ R दिया है इसलिए वास्तविक समूच्य है ।
f (x) = \(\) में f(2) और f(\(\frac {1}{2}\)) का मूल्य ज्ञात करेंगे ।
x = 2 के लिए f(2) = \(\)
x = \(\frac {1}{2}\) अब f(\(\frac {1}{2}\)) =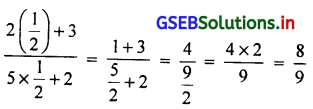
अब f(2). f (\(\frac {1}{2}\)) ज्ञात करने के लिए f(2) = \(\frac {7}{12}\) और f(\(\frac {1}{2}\)) – \(\frac {8}{9}\) रखने पर f(2). f(\(\frac {1}{2}\))
\(\frac {7}{12}\) × \(\frac {8}{9}\)
= \(\frac {506}{108}\) ∴ = \(\frac {14}{27}\)

प्रश्न 13.
यदि f(x) = 2x² + \(\frac{1}{x}\), x ∈ R हो, तो f(3) + f (-3) का मूल्य ज्ञात करो ।
उत्तर :
f(x) = 2x² + \(\frac{1}{x}\) में f(3) और f(-3) ज्ञात करने के लिए x = 3 और x = – 3 रखने पर

f(3) = 2(3)² + \(\frac {1}{3}\)
= 2 × 9 + \(\frac {1}{3}\)
= 18 + 0.33
∴ f(3) = 18.33

f(-3) = 2(-3)² + \(\frac{1}{-3}\)
= 2 × 9 + \(\frac{1}{-3}\)
= 18 – 0.33
∴ f(-3) = 17.67

अब f(3) + f(-3) में f(3) = 18.33 और f(-3) = 17.67 रखने पर
f(3) + f(-3) = 18.33 + 17.67
∴ = 36

प्रश्न 14.
यदि f(x) = 15x³ – 4x² + x + 10, x ∈ R हो, तो \(\) का मूल्य ज्ञात करो ।
उत्तर :
f(x) = 15x³– 4x² + x + 10 में x = 2 और 1 रखने पर

f(2) = 15 (2)³ – 4(2)² + 2 + 10
= 15 × 8 – 4 × 4 + 2 + 10
= 120 – 16 + 2 + 10
= 132 – 16
∴ f(2) = 116

f(1) = 15(1)³ – 4(1) + 1 + 10
= 15 × 1 – 4 + 1 + 10
= 15 – 4 + 1 + 10
= 26 – 4
∴ f(1) = 22
अब \(\frac{f(2)}{f(1)}=\frac{116}{22}=\frac{58}{11}\)
∴ \(\frac{f(2)}{f(1)}\) का मूल्य \(\frac{58}{11}\) होगा ।

प्रश्न 15.
यदि f(x) = \(\sqrt{5600-4 x}\), x ∈ R है । x = 1000 हो, तो f(x) ज्ञात करो और x की कौन-सी किंमत के लिए f(x) = 20
होगा?
उत्तर :
f(x) = \(\sqrt{5600-4 x}\) में x = 1000 रखने पर
∴ f(1000) = \(\sqrt{5600-4(1000)}=\sqrt{5600-4000}=\sqrt{1600}\)
∴ f(1000) = 40
f(x) = 20 दिया है ।
∴ 20 = \(\sqrt{5600-4 x}\) (दो और वर्ग करने पर)
∴ 400 = 5600 – 4x
∴ 4x = 5600 – 400
∴ 4x = 5200
∴ x = \(\frac{5200}{4}\)
∴ x = 1300
f(x) = 40 और x = 1300 होगा ।