GSEB Solutions Class 12 Statistics Part 2 Chapter 1 संभावना Ex 1.4

Gujarat Board Statistics Class 12 GSEB Solutions Part 2 Chapter 1 संभावना Ex 1.4 Textbook Exercise Questions and Answers.

Gujarat Board Textbook Solutions Class 12 Statistics Part 2 Chapter 1 संभावना Ex 1.4

प्रश्न 1.
एक परिवार में 2 शिशु है । यदि प्रथम शिशु लड़की हो, तो उस परिवार के दोनों शिशु लड़कियाँ हो, उसकी संभावना ज्ञात कीजिए।
उत्तर :
यहाँ लड़के को B और लड़की को G संकेत में दर्शाएंगे। एक परिवार में 2 शिशु है इसके कुल परिणाम
∴ U = n = {BB, BG GB, GG} = 4 n = 4
A = प्रथम शिशु लड़की हो वह घटना
∴ A के सानुकूल परिणाम m = {GB. GG} = 2 m = 2
P(A) = \(\frac{m}{n}=\frac{2}{4}=\frac{1}{2}\)
B = दोनों शिशु लड़कियाँ हो ऐसी घटना
∴ B के सानुकूल परिणाम m = {GG} = 1 m = 1
P(B) = \(\frac{m}{n}=\frac{1}{4}\)
A∩B = प्रथम शिशु लड़की हो और दोनों शिशु लड़कियाँ हो A∩B के लिए सानुकूल परिणाम m = (GG) = 1 m = 1
P(A∩B) = \(\frac{m}{n}=\frac{1}{4}\)
प्रथम शिशु लड़की हो ऐसी शर्त पर दोनों शिशु लड़कियाँ हो अर्थात् घटना A बन चुकी है उसी शर्ताधीन घटना B बने उसे संकेत में B/A से दर्शाएंगे।

मांगी गई संभावना = \(\frac {1}{2}\)

प्रश्न 2.
दो संतुलित पासा को एकसाथ उछाला जाता है। यदि दोनों पासा पर के अंकों का योग 7 से अधिक हो, तो दोनों पासों पर समान अंक मिले उसकी संभावना का मान ज्ञात कीजिए।
उत्तर :
दो संतुलित पासों को एकसाथ उछाला जाता है । इस प्रयोग के कुल प्राथमिक परिणाम n = 36,
∴ U = {(i, j) = i, j = 1, 2, 3, 4, 5, 6}
A = दोनों पासों पर के अंकों का योग 7 से अधिक हो तो घटना A के सानुकूल परिणाम
∴ P(A) = \(\frac{m}{n}=\frac{15}{36}=\frac{5}{12}\)
B = दोनों पासों पर समान अंक हो उसे घटना B के सानुकूल परिणाम
B = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)} m = 6
∴ P(B) = \(\frac{m}{n}=\frac{15}{36}=\frac{5}{12}\)
A∩B = दोनों पासों पर का योग 7 से अधिक हो और दोनों पासों पर समान अंक आये ऐसी घटना A∩B के सानुकूल परिणाम {(4,4), (5,5), (6,6)} m = 3
P(A∩B) = \(\frac{m}{n}=\frac{3}{36}=\frac{1}{12}\)
B/A = यदि दोनों पासों पर का योग 7 से अधिक हो, तो दोनों पासों पर समान अंक हो ऐसी घटना

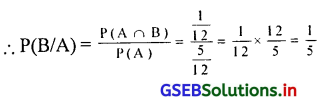
मांगी गई संभावना = \(\frac{1}{5}\)

प्रश्न 3.
पेट्रोल पंप पर आनेवाले परिवहन में से 80% परिवहन चालक अपने परिवहन के साधन में पेट्रोल डलवाने आते है और 60% परिवहन चालक अपने व्हिकल में हवा डलवाने आते है, 50% परिवहन चालक पेट्रोल और हवा दोनों डलवाने आते है, निम्न घटनाओं की संभावना ज्ञात कीजिए।
(1) कोई परिवहन चालक अपने परिवहन में पेट्रोल डलवाने आया हो तो वह चालक अपने परिवहन में हवा डलवाये
(2) कोई परिवहन चालक अपने परिवहन में हवा डलवाने आते है तो वह अपने परिवहन में पेट्रोल डलवाये।
उत्तर :
पेट्रोल पंप पर आनेवाला परिवहन चालक अपने परिवहन में पेट्रोल डलवाये उसे घटना A कहे तो
∴ P(A) = \(\frac{80}{100}=\frac{4}{5}\) अथवा 0.8
पेट्रोल पंप पर आनेवाला परिवहन चालक अपने परिवहन में हवा डलवाये उसे घटना B कहे तो
∴ P(B) = \(\frac{60}{100}=\frac{3}{5}\) अथवा 0.6
पेट्रोल पंप पर आनेवाला परिवहन चालक पेट्रोल और हवा दोनों डलवाये उसे A∩Bकहेंगे।
∴ P(A∩B)= \(\frac{50}{100}=\frac{1}{2}\) = 10.5

(1) कोई परिवहन चालक अपने परिवहन में पेट्रोल डलवाने आते है तो वह चालक अपने परिवहन में हवा डलवाये अर्थात् A बन चुकी है उसी शाधीन B बने उसे B/A कहे तो
∴ P(B/A) = \(\frac{\mathrm{P}(\mathrm{A} \cap \mathrm{B})}{\mathrm{P}(\mathrm{A})}=\frac{0.5}{0.8}=\frac{5}{8}\)
मांगी गई संभावना = \(\frac{5}{8}\)

(2) कोई परिवहन चालक अपने परिवहन में हवा डलवाने आते है तो वह अपने परिवहन में पेट्रोल डलवाये अर्थात् B बन चुकी है उसी शर्ताधीन A
बने उसे A/B कहे तो
∴ P(B/A) = \(\frac{P(A \cap B)}{P(B)}=\frac{0.5}{0.6}=\frac{5}{6}\)
मांगी गई संभावना = \(\frac{5}{6}\)

प्रश्न 4.
एक राष्ट्रीयकृत बैंक में 80% ग्राहक बचत खाता धारक है और 50% ग्राहक चालु खाता धारक है। 90% ग्राहक बचत खाता और चालु (करन्ट) खाता में से कम से कम एक खाता के धारक है। इस बैंक के खाता-धारक में से यादृच्छिक रीति से चयन किया गया ग्राहक चालु (करन्ट ) खाता-धारक हो, तो वह बचत खाता धारक हो उसकी संभावना ज्ञात कीजिए।
उत्तर :
राष्ट्रीयकृत बैंक में ग्राहक बचत खाता धारक हो उसे घटना A कहे तो
∴ P(A) = \(\frac{80}{100}=\frac{4}{5}\) अथवा 0.8
राष्ट्रीयकृत बैंक में ग्राहक चालु (करन्ट) खाता धारक हो उसे घटना B कहे तो
∴ P(B) = \(\frac{50}{100}=\frac{1}{2}\) अथवा 0.5
ग्राहक बचत या चालु (करन्ट) दोनों में से कम से कम एक खाता धारक हो अर्थात् A∪B बने
∴ P(A∪B) = \(\frac{90}{100}=\frac{9}{10}\) अथवा 0.9
अब संभावना के योग के नियम पर से
P(A∪B) = P(A) + P(B)- P(A∩B)
0.9 = 0.8 + 0.5- P(A∩B)
∴ P(A∩B)= 1.3 – 0.9 = 0.4
A/B = ग्राहक चालु (करन्ट) खाता धारक हो, तो वह बचत खाता धारक हो वह घटना अर्थात् घटना B बन चुकी है उसी शर्ताधीन A बने
∴ P(A/B) = \(\frac{\mathrm{P}(A \cap B)}{\mathrm{P}(\mathrm{B})}=\frac{0.4}{0.5}=\frac{4}{5}\)
मांगी गई संभावना = \(\frac{4}{5}\)

प्रश्न 5.
एक यादृच्छिक प्रयोग के निदर्श अवकाश की कोई दो घटनाएँ के लिए P(A) = \(\frac {2}{3}\), P(B) = \(\frac {3}{5}\) और P(B/A) = \(\frac {3}{4}\) हो, तो P(A/B) ज्ञात कीजिए।
उत्तर :
यहाँ P(A) = \(\frac {2}{3}\) P(B) = \(\frac {3}{5}\) और P(B/A) = \(\frac {3}{4}\) दिया है।
P(B/A) सूत्र पर से प्राप्त P(A∩B) प्राप्त करेंगे।

प्रश्न 6.
यदि घटनाएँ A, M और F के लिए P(M) = P(F) = \(\frac {1}{2}\) हो तथा P{A/M) = \(\frac {1}{10}\) और P(A/F} = \(\frac {1}{2}\) हो, तो P (A∩M)और P(A∩F) ज्ञात कीजिए।
उत्तर :
P(M) = P(F) = \(\frac {1}{2}\)
∴ P(M) = \(\frac {1}{2}\) और P(F) = \(\frac {1}{2}\) P(A/M) = \(\frac {1}{10}\) P(A/F) = P(A/F) = \(\frac {1}{2}\)
P(A/M) = \(\frac{P(A \cap M)}{P(M)}\)
∴ P(A∩M) = P(A/M) × P(M)= \(\frac{1}{10} \times \frac{1}{2}=\frac{1}{20}\)
P(A/F) = \(\frac{P(A \cap F)}{P(F)}\)
∴ P(A∩F) = P(A/F) × P(F) = \(\frac{1}{2} \times \frac{1}{2}\)
∴ P(A∩F) = \(\frac {1}{4}\)
मांगी गई संभावना = P(A∩M) = \(\frac {1}{20}\) अथवा 0.05 और P(A∩F) = \(\frac {1}{4}\) अथवा 0.25

प्रश्न 7.
एक संदूक में 2 सोने और 4 चांदी के सिक्के है । जब कि दूसरी संदूक में 3 सोने और 5 चांदी के सिक्के हैं। प्रत्येक संदूक में से यादृच्छिक रीति से एक-एक सिक्का चयन किया जाता है। चयन हुए दो सिक्कों में एक सिक्का सोने और एक सिक्का चांदी का होने की संभावना ज्ञात कीजिए।
उत्तर :
एक सिक्का सोने और एक सिक्का चांदी हो यह घटना दो प्रकार से बन सकती है। (1) प्रथम संदूक में सोना (G₁) और दूसरी संदूक में चांदी (S₂) सिक्के अथवा (2) प्रथम संदूक में चांदी (S₁) और दूसरी संदूक में सोना (G₂) सिक्के हो उसे घटना A कहे तो
P = (G₁∩S₂)∪P(S₁∩₂) दोनों घटनाएँ परस्पर निवारक है।
∴ P(A) = P(G₁∩S₂) + P(S₁∩G₂)
लेकिन दोनों संदूक से चुनी गई घटनाएँ निरपेक्ष है इसलिए
P(A) = P(G₁) × P(S₂) + P(S₁) × P(G₂)
प्रत्येक की संभावना प्राप्त करे तो
P(G₁) = प्रथम संदूक में चुना गया सिक्का सोने का हो = \(\frac {2}{6}\)
P(S₂) = दूसरी संदूक में चुना गया सिक्का चांदी का हो = \(\frac {5}{8}\)
P(S₁) = प्रथम संदूक में चुना गया सिक्का चांदी का हो = \(\frac {4}{6}\)
P(G₂) = दूसरी संदूक में चुना गया सिक्का चांदी का हो = \(\frac {3}{8}\)
उपर्युक्त मान को सूत्र में रखने पर ∴ P(A) = \(\frac{2}{8} \times \frac{5}{5}+\frac{4}{6} \times \frac{3}{8}\)
∴ P(A) = \(\frac{10}{48}+\frac{12}{48}=\frac{22}{48}\)
∴ P(A) = \(\frac{11}{24}\)
मांगी गई संभावना = \(\frac{11}{24}\)

प्रश्न 8.
एक संयुक्त परिवार में 3 लड़के और 2 लड़कियाँ है। जबकि दूसरे संयुक्त परिवार में 2 लड़के और 4 लड़कियाँ है। इन दो संयुक्त परिवार में से एक संयुक्त परिवार चयन करके इसमें से यादृच्छिक रीति से एक शिशु चयन किया जाय तो, वह लड़की होने की संभावना ज्ञात कीजिए।
उत्तर :
दो संयुक्त परिवार में से एक परिवार का चयन किया जाता है।
A = प्रथम परिवार चयन हो ऐसी घटना ∴ P(A) = \(\frac {1}{2}\)
B = दूसरा परिवार चयन हो ऐसो घटना ∴ P(B) = \(\frac {1}{2}\)
प्रथम परिवार में 3 लड़के और 2 लड़कियाँ है । कुल 5 शिशु में से एक शिशु चयन करने के कुल परिणाम n = ₅C₁ = 5
G₁ = प्रथम परिवार में लड़की चयन हो वह घटना G₁ के लिए सानुकूल परिणाम m = ₂C₁ = 2
∴ P(G₁) = \(\frac{m}{n}=\frac{2}{5}\)
दूसरा परिवार में 2 लड़के 4 लड़कियाँ है। कुल 6 शिशु में से एक शिशु चयन करने के कुल परिणाम ₆C₁ = 6 n = 6
G₂ = दूसरा परिवार में लड़की का चयन हो वह घटना G₂ के लिए सानुकूल परिणाम m = ₄C₁ 4 m = 4
∴ P(G₂) = \(\frac{m}{n}=\frac{4}{6}=\frac{2}{3}\)

A∩G₁ = प्रथम परिवार का चयन हो और उसमें से लड़की का चयन हो वह घटना
∴ P(A∩G₁) = P(A) × P(G₁) = \(\frac{1}{2} \times \frac{2}{5}=\frac{1}{5}\)
B∩G₂ = दूसरा परिवार का चयन हो और उसमें से लड़की का चयन हो वह घटना
∴ P(B∩G₂) = P(B) × P(G₂) = \(\frac{1}{2} \times \frac{2}{3}=\frac{1}{3}\)
चुना गया शिशु लड़की हो उसकी संभावना
∴ P(A∩G₁) (B∩G₂) = P(A∩G₁)+P(B∩G₂) = \(\frac{1}{5}+\frac{1}{3}=\frac{3+5}{15}=\frac{3}{15}\)
मांगी गई संभावना = \(\frac{8}{15}\)

प्रश्न 9.
एक बॉक्स में 10 आइसक्रीम कोन है जिसमें से 3 कोन का वजन नियत किया गया वजन से कम है और शेष 7 कोन का वजन नियत किया वजन जितना है। इस बॉक्स में से एक के बाद एक ऐसे दो कोन पुरवणी सहित यादृच्छिक रीति से पसंद किया जाता है। चयन किया गया दोनों कोन नियत वजन से जनताले होने की संभावना ज्ञात कीजिए।
उत्तर :
10 आईस्क्रीम कोन में से यादृच्छिक रूप से पूर्ति सहित एक के पश्चात् एक ऐसे दो कोन का चुनाव के प्रकार कुल
₁₀C₁ × ₁₀C₁ = 10 × 10 = 100
इन समग्र चुनाव के प्रकार परस्पर निवारक एवं समसंभावी कहेंगे इसलिए निदर्श अवकाश के घटक के परिणाम n = 100
प्रथम चयन में कोन नियत वजन से कम हो उस घटना को A कहे तो A के सानुकूल परिणाम ₃C₁ = 3 m = 3
∴ P(A) = \(\frac{3}{10}\)
दूसरा चयन में कोन नियत वजन से कम हो उस घटना को B कहे तो चयन पूर्ति सहित है।
∴ B के सानुकूल परिणाम m = ₃C₁ = 3 m = 3
∴ P(B) = \(\frac{m}{n}=\frac{3}{10}\)
दोनों कोन नियत वजन से कम वजनवाले हो उसे घटना A∩B कहे तो दोनों घटनाएँ निरपेक्ष है।
∴ निरपेक्ष घटना की परिभषा के अनुसार
∴ P(A∩B) = P(A) × P(B) = \(\frac{3}{10} \times \frac{3}{10}=\frac{9}{100}\)
मांगी गई संभावना = \(\frac{9}{100}\)

प्रश्न 10.
फिल्म सीडी रखने के एक रेंक में कुल 10 सी.डी. है। जिसमें 6 सी.डी. एकसन फिल्म की और 4 सीडी ड्रामा फिल्म की है। इस रेंक में से एक के पश्चात एक ऐसे दो सी.डी. पूर्ति रहित पद्धति से याद्दच्छिक रीति से चयन की जाती है। चयन हुई दो सी.डी. में प्रथम सी.डी. एकसन फिल्म की और दूसरी सी.डी. ड्रामा फिल्म की हो उसकी संभावना ज्ञात कीजिए।
उत्तर :
10 सी.डी. में से याद्दच्छिक रूप से पूर्ति रहित एक के पश्चात एक ऐसे दो सी.डी. चयन की जाती है। चुनाव के कुल प्रकार
₁₀C₁ × ₉C₁ = 10 × 9 = 90 होगा।
प्रथम चयन में सी.डी. एक्शन फिल्म की हो उसे घटना A कहे तो A के लिए सानुकूल परिणाम m = ₆C₁ = 6 m = 6
∴ P(A) = \(\frac{6}{10}\)
दूसरा चयन में सी.डी. ड्रामा फिल्म की हो उसे घटना B कहे तो B के लिए सानुकूल परिणाम M = ₄C₁ = 4 m = 4
दूसरा चयन करते समय रेंक में 9 सी.डी. होगी (प्रथम चुनाव की गई एक्शन फिल्म की सी.डी. वापस नहि रखा जायेगा) इसलिए कुल परिणाम n = ₉C₁ = 9 n = 9
∴ P(B) = \(\frac{4}{9}\)
दोनों घटनाएँ निरपेक्ष है।
∴ P(A∩B) = P(A) × P(B) = \(\frac{6}{10} \times \frac{4}{9}=\frac{24}{90}=\frac{4}{15}\)
मांगी गई संभावना = \(\frac{4}{15}\)

प्रश्न 11.
दो संतुलित पासा एकसाथ उछाला जाय तो,
(1) कम से कम एक पासा पर अंक 5 मिले उसकी संभावना
(2) प्रथम पासा पर अंक 5 या 6 मिले और दूसरा पासा पर युग्म पूर्णांक मिले उसकी संभावना ज्ञात करो।
उत्तर :
(1) कम से कम एक पासा पर अंक 5 मिले उसकी संभावना प्रथम पासा पर अंक 5 मिले उसे घटना = A
दूसरा पासा पर अंक 5 मिले उसे घटना = B, कम से कम एक पासा पर अंक 5 मिले उसे घटना = A∪B
घटना A के सानुकूल परिणाम m = 1 घटना A की संभावना P(A) = \(\frac{\mathrm{m}}{\mathrm{n}}=\frac{1}{6}\)
घटना B के सानुकूल परिणाम m = 1 घटना B की संभावना P(B) = \(\frac{\mathrm{m}}{\mathrm{n}}=\frac{1}{6}\)

मांगी गई संभावना = \(\frac {11}{36}\)

(2) प्रथम पासा पर अंक 5 या 6 मिले और दूसरा पासा पर पूर्णांक मिले उसकी संभावना
A₁ = प्रथम पासा पर अंक 5 या 6 मिले वह घटना
B₁ = दूसरा पासा पर अंक पूर्णांक मिले वह घटना
प्रथम पासा पर अंक 5 या 6 मिले और दूसरा पासा पर पूर्णांक मिले उसे (A₁∩B₁) कहे तो घटना A₁ के सानुकूल परिणाम m = 2
∴ P(A₁) = \(\frac{m}{n}=\frac{2}{6}\)
घटना B₁ के सानुकूल परिणाम m = 3 पूर्णांक अंक (2, 4, 6)
∴ P(B₁) = \(\frac{m}{n}=\frac{3}{6}\)
अब A₁ और B₁ निरपेक्ष घटनाएँ है।
∴ P(A₁∩B₁) = P(A₁) × P(B₁) = \(\)
मांगी गई संभावना = \(\frac{2}{6} \times \frac{3}{6}=\frac{6}{36}=\frac{1}{6}\)

प्रश्न 12.
संभावना का सवाल तानिया, कथन और कीर्ति को हल करने के लिए दिया जाता है। वह सवाल सही हल कर सके उसकी
संभावना क्रमश: \(\frac {2}{3}\), \(\frac {3}{4}\) और \(\frac {1}{2}\)
सवाल सही गिना जाय उसकी संभावना ज्ञात कीजिए।
उत्तर :
तानिया सवाल सही हल कर सके उसे घटना A कहे तो ∴ P(A) = \(\frac {2}{3}\)
कथन सवाल सही हल कर सके उसे घटना B कहे तो ∴ P(B) = \(\frac {3}{4}\)
कीर्ति सवाल सही हल कर सके उसे घटना C कहे तो ∴ P(C) = \(\frac {1}{2}\)
घटना A की पूरक घटना P(A’) = 1 – \(\frac{2}{3}=\frac{1}{3}\)
B की पूरक घटना P(B’)= 1 – \(\frac{3}{4}=\frac{1}{4}\)
C की पूरक घटना P(C)= 1 – \(\frac{1}{2}=\frac{1}{2}\)

सवाल सही हल हो सके अर्थात् A, B, C में से कम से कम एक घटना घटे अर्थात् P(A∪B∪C) बने । तीनों सवाल हल न कर सके अर्थात् P(A’∩B’∩C’) बने.
अब P(A∪B∪C) + P(A’∩B’∩C’) = 1
∴ P(A∪B∪C)= 1- P(A’∩B’∩C’) = 1- [P(A’) x P(B’) x P(C’)]
1 – \(\frac{1}{3} \times \frac{1}{4} \times \frac{1}{2}\) = 1 – \(\)
मांगी गई संभावना = \(\frac{1}{24}=\frac{24-1}{24}=\frac{23}{24}\)

प्रश्न 13.
एक व्यक्ति A यह 5 में से 3 प्रयत्नों में निशाना लगा सकता है जबकि व्यक्ति B यह 6 में से 5 प्रयत्नों में निशाना लगा सकता है। यदि दोनों व्यक्ति एकसाथ निशाना लगाये तो निशाना लग जाय उसकी संभावना ज्ञात कीजिए।
उत्तर :
A व्यक्ति 5 में से 3 प्रयत्नों मे निशाना लगा सके उसे घटना A₁ कहे तो A₁ की संभावना ∴ P(A₁) = \(\frac {3}{5}\)
B व्यक्ति 6 में से 5 में निशाना लगा सके उसे घटना B, कहे तो B, की संभावना ∴P(B₁) = \(\frac {5}{6}\)

प्रश्न 14.
व्यक्ति A यह 90% किस्से में सत्य बोलता है जबकि व्यक्ति B यह 80% किस्से में सत्य बोलता है। व्यक्तियों A और B एक ही विधान प्रस्तुत करने में भिन्न हो जाय उसकी संभावना ज्ञात कीजिए।
उत्तर :
व्यक्ति A 90% किस्से में सत्य बोलता है। ∴ उसकी संभावना = \(\frac{90}{100}\) = 0.9 ∴ P(A)= 0.9
व्यक्ति B 80% किस्से में सत्य बोलता है। ∴ उसकी संभावना = \(\frac{80}{100}\) = 0.8 ∴ P(B) = 0.8
व्यक्ति A असत्य बोले अर्थात् A की पूरक घटना A’ बने PKA’) = 1 – 0.9 = 0.1 ∴ P(A’) = 0.1
व्यक्ति B असत्य बोले अर्थात् B की पूरक घटना B’ बने P(B’) = 1 – 0.8 – 0.2 ∴ P(B’)= 0.2
A और B एक ही विधान प्रस्तुत करने में भिन्न हो अर्थात् A सत्य बोले और B असत्य बोले अर्थात् P(A)∩P(B’) B
सत्य बोले और A असत्य बोले अर्थात् P(B)∩P(A’), P(A∩B’) + P(B∩A’) बने
∴ P(A∩B’) + P(B∩A’) = P(A) × P(B’) + P(B) × P(A’)
= 0.9 × 0.2 + 0.8 × 0.1 = 0.18 + 0.08 = 0.26
मांगी गई संभावना = 0.26

प्रश्न 15.
यदि यादृच्छिक प्रयोग की तीन घटनाएं A और B और C निरपेक्ष घटनाएं हो और P(A) = 0.2, P(B) = 0.3 एवं P(C) = 0.5 हो, तो P(A∪B∪C) ज्ञात कीजिए।
उत्तर :
A, B, C तीन घटनाएं निरपेक्ष है इसलिए P(A∩B) = P(A) × P(B) P(B∩C) = P(B) × P(C) P(A∩C) = P(A) × P(C) और
P(A∩B∩C) = P(A) × P(B) × P(C)
अब योग का नियम अनुसार P(A∪B∪C) = P(A) + P(B) + P(C) – P(A∩B) – P(A∩C) – P(B∩C) + P(A∩B∩C)
तीनों घटनाएं निरपेक्ष है इसलिए योग के नियम को निम्नानुसार लिखेंगे।
P(A∪B∪C) = P(A) + P(B) + P(C) – P(A) × P(B) – P(A) × P(C) – P(B) × P(C) + P(A) × P(B) × P(C)
= 0.2 + 0.3 + 0.5-(0.2 × 0.3)-(0.2 × 0.5)-(0.3 × 0.5) + (0.2 × 0.3 × 0.5)
= 1.0 – 0.06 – 0.10 – 0.15 + 0.03
∴ P(A∪B∪C) = 0.72
मांगी गई संभावना = 0.72