GSEB Solutions Class 12 Statistics Part 2 Chapter 4 लक्ष Ex 4

Gujarat Board Statistics Class 12 GSEB Solutions Part 2 Chapter 4 लक्ष Ex 4 Textbook Exercise Questions and Answers.

Gujarat Board Textbook Solutions Class 12 Statistics Part 2 Chapter 4 लक्ष Ex 4

विभाग – A

निम्न दिये गए विकल्पों में से सहि विकल्प चयन करके लिखिए ।

प्रश्न 1.
3 का 0.3 सामीप्य का मानांक स्वरूप कौन-सा है ?
(a) |x – 0.3| < 3
(b) |x – 3| < 0.3
(c) |x + 3| < 0.3 (d) |x- 3| > 0.3
उत्तर :
(b) |x – 3| < 0.3

प्रश्न 2.
-2 का 0.02 सामीप्य का अंतराल स्वरूप कौन-सा है ?
(a) (1.98, 2.02)
(b) (-1.98, 2.02)
(c) (-2.02, -1.98)
(d) (-2.02, 1.98)
उत्तर :
(c) (-2.02, -1.98)

प्रश्न 3.
|x – 5| < 0.25 का अंतराल स्वरूप कौन-सा है ?
(a) (4.75, 5.25)
(b) (-4.75, 5.25)
(c) (-5.25, -4.75)
(d) (-5.25, 4.75)
उत्तर :
(a) (4.75, 5.25)

प्रश्न 4.
|2x + 1| < \(\frac {1}{5}\) का अंतराल स्वरूप कौन-सा है ?
(a) (\(\frac {-6}{5}\), \(\frac {-4}{5}\) )
(b) (\(\frac {-6}{10}\), \(\frac {-4}{10}\))
(c) (\(\frac {4}{10}\), \(\frac {6}{10}\))
(d) (\(\frac {-6}{10}\), \(\frac {4}{10}\))
उत्तर :
(b) (\(\frac {-6}{10}\), \(\frac {-4}{10}\))

प्रश्न 5.
N(5, 0.02) का मानांक स्वरूप कौन-सा है?
(a) |x + 5| < 0.02
(b) |x – 0.02| < 5 (c) |x – 5| > 0.02
(d) |x – 5| < 0.02
उत्तर :
(d) |x – 5| < 0.02

प्रश्न 6.
यदि N(a, 0.07) का मानांक स्वरूप |x – 10| < k हो, तो k का मूल्य कितना होगा?
(a) a
(b) 0.7
(c) 0.07
(d) 9.93
उत्तर :
(c) 0.07

प्रश्न 7.
\(\lim _{x \rightarrow 3} 3 x-1\)का मूल्य कितना होगा?
(a) 9
(b) 10
(c) \(\frac {4}{3}\)
(d) 8
उत्तर :
(d) 8

प्रश्न 8.
\(\lim _{x \rightarrow 4} \sqrt{4 x+9}\) का मूल्य क्या होगा?
(a) 5
(b) 25
(c) \(\frac {7}{4}\)
(d) 7
उत्तर :
(a) 5

प्रश्न 9.
\({Lim}_{x \rightarrow-2} 10\) का मूल्य क्या होगा?
(a) 10
(b) -2
(c) 8
(d) अनियत
उत्तर :
(a) 10

प्रश्न 10.
\(\lim _{x \rightarrow 3} \frac{x^4-81}{x-3}\) का मूल्य क्या होगा?
(a) 192
(b) 324
(c) 36
(d) 108
उत्तर :
(d) 108

प्रश्न 11.
\(\lim _{x \rightarrow-1} \frac{x^5+1}{x+1}\) का मूल्य क्या होगा?
(a) -5
(b) 5
(c) 4
(d) -4
उत्तर :
(b) 5

प्रश्न 12.
यदि y = 10 – 3x हो और x → -3 हो, तोy के कौन से मूल्य को अनुलक्षित है?
(a) 1
(b) 9
(c) 19
(d) 7
उत्तर :
(c) 19

विभाग – B

निम्न प्रश्नों के एक वाक्य में उत्तर दीजिए ।

प्रश्न 1.
0 का 0.09 सामीप्य को अंतराल स्वरूप में प्रदर्शित कीजिए।
उत्तर :
0 का 0.09 सामीप्य को a का δ सामीप्य के साथ तुलना करने पर a = 0 और δ = 0.09 प्राप्त होगा।
अंतराल स्वरूप : (a – δ, a + δ), a = 0 और δ = 0.09 रखने पर (0-0.09,0 + 0.09) = (-0.09,0.09)

प्रश्न 2.
-5 का 0.001 सामीप्य को मानांक स्वरूप में प्रदर्शित कीजिए।
उत्तर :
-5 का 0.001 सामीप्य को a का δ सामीप्य के साथ तुलना करने पर a = -5 और δ = 0.001 प्राप्त होगा।
मानांक स्वरूप में : |x – a| < δ, a = -5 और δ = 0.001 रखने पर -5 का 0.001 सामीप्य = |x + 5| < 0.001

प्रश्न 3.
|x – 10|< \(\frac{1}{10}\) को सामीप्य स्वरूप में प्रदर्शित कीजिए।
उत्तर :
|x – 10| < \(\frac{1}{10}\) को |x – a| < δ के साथ तुलना करने पर हमें a = +10, δ = \(\frac{1}{10}\)प्राप्त होता है।
सामीप्य स्वरूप : N (a, δ ), a = + 10, δ = \(\frac{1}{10}\) रखने पर |x – 10 < \(\frac{1}{10}\) = N(1o, \(\frac{1}{10}\) )

प्रश्न 4.
|2x| < \(\frac{1}{2}\) को अंतराल स्वरूप में प्रदर्शित कीजिए।
उत्तर :
|2x| < \(\frac{1}{2}\) को |x – a| < δ के साथ तुलना करने पर हमें a = \(\frac{1}{4}\) और δ = \(\frac{1}{2}\) प्राप्त होगा।
अंतराल स्वरूप में : (a – δ, a + δ ), a = \(\frac{1}{4}\) और δ = \(\frac{1}{2}\) रखने पर |2x| <
\(\frac{1}{2}\) = (\(\frac{1}{4}-\frac{1}{2}, \frac{1}{4}+\frac{1}{2}\)) = (\(-\frac{1}{4}, \frac{3}{4}\))

प्रश्न 5.
N(50, 0.8) को मानांक स्वरूप में प्रदर्शित कीजिए।
उत्तर :
N(a, δ) के साथ तुलना करने पर a = 50 और δ = 0.8 प्राप्त होगा।
मानांक स्वरूप में : |x – a| < δ, a = 50 का δ = 0.8 रखने पर 50 का 0.8 सामीप्य = |x – 50| < 0.8

प्रश्न 6.
यदि N(a, 0.2) = |x – 7| < b हो, तो a का मूल्य ज्ञात कीजिए।
उत्तर :
N(a, δ) = |x – a| < b के साथ तुलना करने पर N(a, 0.2) है ∴ δ = 0.2,
|x – 7| < b हो, तो a = +7 प्राप्त होगा । अर्थात् a = 7 और b = 0.2

प्रश्न 7.
यदि |x + 4 | < 0.04 = (k – 3.96) हो, तो k का मूल्य ज्ञात कीजिए।
उत्तर :
|x – a| < δ को |x + 4|< 0.04 के साथ तुलना करने पर a = -4 और δ = 0.04 प्राप्त होगा। अब अंतराल स्वरूप (a – δ, a + δ में
a – δ = k में a = -4 और 0.04 रखने पर -4 – 0.04 = k
∴ k = -4.04

प्रश्न 8.
\(\lim _{x \rightarrow 5^{(}}(3 x+5)\) का मूल्य ज्ञात कीजिए।
उत्तर :
x = 5 रखने पर \(\lim _{x \rightarrow 5}(3 x+5)=3(5)+5=15+5=20\)
\(\lim _{x \rightarrow 5}(3 x+5)=20\)

प्रश्न 9.
\(\lim _{x \rightarrow-3} \sqrt[3]{2-2 x}\) का मूल्य ज्ञात कीजिए।
उत्तर :
\(\lim _{x \rightarrow-3} \sqrt[3]{2-2 x}\) में x = -3रखने पर = \(\sqrt[3]{2-2(-3)}=\sqrt[3]{2+6}=\sqrt[3]{8}\) घनमूल करने पर = 2
∴ \(\lim _{x \rightarrow-3} \sqrt[1]{2-2 x}=2\)

प्रश्न 10.
\(\lim _{x \rightarrow 0}\left(\frac{3 x^2-4 x+10}{2 x+5}\right)\) का मूल्यज्ञात काजिए।
उत्तर :

प्रश्न 11.
\(\lim _{x \rightarrow 2} \frac{x^5-32}{x-2}\) का मूल्य ज्ञात कीजिए।
उत्तर :
यदि x = 2 रखने से फलन का मूल्य \(\frac{0}{0}\) प्राप्त होता है, जो अनियत है।

प्रश्न 12.
\(\lim _{x \rightarrow-a} \frac{x^n+a^m}{x+a}\) (जहाँ m विषम संख्या है) का मूल्य ज्ञात कीजिए।
उत्तर :
x → -a रखने से फलन का मूल्य में \(\frac{0}{0}\) प्राप्त होता है जो अनियत है।

प्रश्न 13.
\(\lim _{x \rightarrow-1} 4 x+k=6\) हो, तोk का मूल्य ज्ञात कीजिए।
उत्तर :
\(\lim _{x \rightarrow-1} 4 x+k=6\) में x = -1 रखने पर
4(-1) + k = 6
-4 + k = 6
∴ k = 6 + 4
∴ k = 10

प्रश्न 14.
\(\lim _{x \rightarrow 3} \frac{2}{3 x+k}=\frac{1}{7}\) हो, तो k का मूल्य ज्ञात कीजिए।
उत्तर:
\(\lim _{x \rightarrow 3} \frac{2}{3 x+k}=\frac{1}{7}\) में x = 3 रखने पर
\(\frac{2}{3(3)+\mathrm{k}}=\frac{1}{7}\)
\(\frac{2}{9+k}=\frac{1}{7}\)
9 + k = 14
∴ k = 14 – 9
∴ k = 5

विभाग – C

निम्न प्रश्नों के उत्तर दीजिए ।

प्रश्न 1.
विवृत्त अंतराल की परिभाषा दीजिए।
उत्तर :
यदि a ∈ R, b ∈ R और a < b तो a और b को समाविष्ट नहि करती लेकिन a और b के बीच की सभी वास्तविक संख्याओं के समुच्चय
को विवृत्त अंतराल कहते है। विवृत्त अंतराल को (a, b) से दर्शाया जाता है। (a, b) = {x/a < x < b, x ∈ R}

प्रश्न 2.
a का δ सामीप्य की परिभाषा दीजिए।
उत्तर :
यदि a ∈ R और δ यह अऋण वास्तविक संख्या हो, तो विवृत्त अंतराल (a – δ, a + δ) को a का δ सामीप्य कहते है। उसे N(a, δ) से दर्शाया जाता है।

प्रश्न 3.
a का δ छिद्रित सामीप्य की परिभाषा दीजिए।
उत्तरः
यदि a ∈ R और δ यह अऋण वास्तविक संख्या हो, तो विवृत्त अंतराल (a – δ, a + δ)- {a} को a का छिद्रित δ सामीप्य कहते है। उसे N*(a, δ) से दर्शाया जाता है।

प्रश्न 4.
अंतराल स्वरूप(-0.5, 0.5) को मानांक स्वरूप में दर्शाइए।
उत्तर :
अंतराल स्वरूप : (a – δ, a + δ): a – δ = -0.5 और a + δ = 0.5 दोनों का योग करने पर
a – δ = -0.5
\(\frac{a+\delta=0.5}{2 a=0}\)
∴ a = 0
अब a + δ = 0.5 में a = 0 रखने पर 0 + δ = 0.5
∴ δ = 0.5
मानांक स्वरूप : |x – a| < δ में a = 0 और δ = 0.5 रखने पर
∴ |x – 0 | < 0.5 ∴ |x| < 0.5

प्रश्न 5.
अंतराल स्वरूप (-8.75, -7.25) को सामीप्य स्वरूप मे दर्शाइए।
उत्तरः
अंतराल स्वरूप : (a – δ, a + δ) के साथ तुलना करने पर a – δ = -8.75 और a + δ = -7.25 का योग करने पर
a – δ = -8.75
\(\frac{\mathrm{a}+\delta=-7.25}{2 \mathrm{a}=-16}\)
∴ a = -8
a + δ = -7.25 में a = -8 रखने पर
-8 + δ = -7.25
δ = -7.25 + 8
δ = 0.75
अब सामीप्य स्वरूप में : N(a, δ) में a =- 8 और δ = 0.75 रखने पर
∴ N(-8, 0.75)

प्रश्न 6.
यदि N(k, 0.5) = (19.5k₂) हो, तो k₁ और k₂ का मूल्य ज्ञात कीजिए।
उत्तरः
सामीप्य स्वरूप :N(a – δ) के साथ तुलना करने पर a = k₁ और δ = 0.5 प्राप्त होगा।
अंतराल स्वरूप : (a – δ, a + δ) के साथ तुलना करने पर a – δ = 19.5 और a + δ = k₂
a – δ = 19.5 में δ = 0.5 रखने पर a – 0.5 = 19.5
∴ a = 19.5 + 0.5
∴ a = 20
∴ a = k₁ = 20
∴ k₁ = 20
अब a + δ = k₂ में a = 20 और δ = 0.05 रखने पर 20 + 0.5 = k₂
∴ k₂ = 20.5

प्रश्न 7.
|3x + 1| < 2 को सामीप्य और अंतराल स्वरूप में दर्शाइए।
उत्तर :
|x – a| < δ
सामीप्य स्वरूप = N(a – δ) = N (\(\frac{-1}{3}\), \(\frac{2}{3}\))
मानांक स्वरूप के साथ तुलना करने पर |x + \(\frac{1}{3}\)| < \(\frac{2}{3}\) उसे भाग देने पर
|x – \(\frac{-1}{3}\)| < \(\frac{2}{3}\) = a = \(\frac{-1}{3}\) δ = \(\frac{2}{3}\)
|3x + 1| < 2
अंतराल स्वरूप = (a – δ.a + δ) = (\(\frac{-1}{3}\), \(\frac{-2}{3}\)), (\(\frac{-1}{3}\) + \(\frac{2}{3}\) ) = (-1, \(\frac{1}{3}\))

प्रश्न 8.
यदि |x – A₁| < 0.09 = (A₂, 4.09) हो, तो A₁ और A₂ का मूल्य ज्ञात कीजिए।
उत्तर :
|x – A₁|< 0.09 को मानांक स्वरूप |x – a| < δ के साथ तुलना करने पर a = A₁ और δ = 0.09
अंतराल स्वरूप : (a – δ, a + δ) के साथ तुलना करने पर a – δ = A₂ a + δ = 4.09 में δ = 0.09 रखने पर
a + 0.09 = 4.09
∴ a = 4.09 – 0.09
∴ a = 4
अब a – δ = A₂ में a = 4, δ = 0.09 रखने पर
4 – 0.09 = A₂
∴ A₂ = 3.91
a = A₁
∴ a = A₁ = 4
∴ A₁ = 4 और A₂ = 3.91

प्रश्न 9.
x → a का अर्थ समझाइए।
उत्तर :
यदि किसी चल x का मूल्य, कम करने या बढ़ाने पर किसी एक निश्चित संख्या ‘a’ के अधिक नजदीक लाया जाय तो x, a को अनुलक्षित है ऐसा कहा जाता है। उसे संकेत में x → a से दर्शाया जाता है।

प्रश्न 10.
x → 0 का अर्थ समझाइए।
उत्तर :
यदि किसी चल x का धन किंमतें कम करने पर या x की ऋण किंमत में वृद्धि करने पर ‘0’ के अधिक नजदीक लाया जाय तो x, 0 को अनुलक्षित है ऐसा कहा जाता है, उसे संकेत में x → 0 से दर्शाया जाता है।

प्रश्न 11.
फलन के लक्ष की परिभाषा दीजिए।
उत्तर :
यदि कितनी ही छोटी दी गई पूर्व निर्धारित संख्या Σ > 0 के लिए हम ऐसी एक धन संख्या δ ज्ञात कर सके कि जिससे जब |x → a| < हो तब x की प्रत्येक किंमत के लिए |f(x) – 1| < Σ हो, तो जब x, a को अनुलक्षित हो तब फलन f(x) लक्ष 1 को धारण करता है।

प्रश्न 12.
लक्ष का गुणाकार का कार्य नियम लिखिए।
उत्तर :
\(\lim _{x \rightarrow a}[f(x) \times g(x)]=L \times m\) दो फलन का गुणाकार का लक्ष उस दो फलन के लक्ष के गुणाकार बराबर होता है।

प्रश्न 13.
लक्ष का भागाकार का कार्य नियम लिखिए।
उत्तर :
\(\lim _{x \rightarrow a}\left[\frac{f(x)}{9(x)}\right]=\frac{L}{m}\)
m ≠ 0 दो फलनों का भागाकार का लक्ष उसके लक्ष के भागाकार बराबर होता है। यहाँ हर का फलन का लक्ष शून्य (0) होना नहि चाहिए।

प्रश्न 14.
बहुपदी के लक्ष का प्रामाणित रूप बताइए।
उत्तर :
माना कि f(x) = a₀ + a₁x + a₂x² +……….+ a_nxⁿ हो, तो लक्ष के कार्ल नियमों का उपयोग करके
(1) \(\lim _{x \rightarrow a} f(x)\) = a₀ + a₁b + a₂b² +……….+ a_nbⁿ
(2) \(\lim _{x \rightarrow a}\left[\frac{x^n-a^n}{x-a}\right]\) na^{n – 1} n ∈ Q

विभाग – D

निम्न के मूल्य ज्ञात कीजिए ।

प्रश्न 1.
\(\lim _{x \rightarrow 1} \frac{3 x^2-4 x+1}{x-1}\)
उत्तर :
यदि x = 1 रखने पर फलन f(x) का मूल्य \(\frac{0}{0}\) प्राप्त होगा जो अनियत है। इसलिए अंश और हर के अवयव करके x → 1 है इसलिए
(x – 1) अंश औ दूर का सामान्य अवयव है।
अंश = 3x² – 4x + 1
= 3x² – 3x – x + 1
= 3x (x – 1) -1 (x – 1)
= (x – 1) (3x – 1) हर = x – 1

प्रश्न 2.
\(\lim _{x \rightarrow 3} \frac{x-3}{2 x^2-3 x-9}\)
उत्तर :
यदि x = 3 रखने पर फलन f(x) का मूल्य \(\frac{0}{0}\) प्राप्त होगा जो अनियत है इसलिए अंश और हर के अवयव करके x → 3 है इसलिए (x – 3) अंश और हर का सामान्य अवयव है।
अंश = x – 3 हर = 2x² – 3x – 9
=2x² – 6x + 3x -9
= 2x (x – 3) + 3(x – 3)
= (x – 3) (2x + 3)

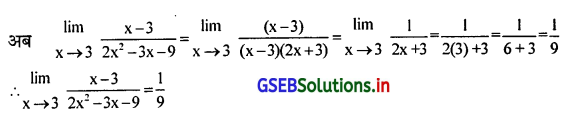
प्रश्न 3.
\(\lim _{x \rightarrow-1} \frac{3 x^2-2 x-5}{x+1}\)
उत्तर :
यदि x → -1 रखने पर फलन f(x) का मूल्य 0 प्राप्त होता है जो अनियत है इसलिए अंश का अवयव का सामान्य x + 1 और हर में x + 1 है।
अंश = 3x² – 2x -5
= 3x² + 3x – 5x – 5
= 3x(x + 1) – 5(x + 1)
= (x + 1) (3x – 5) हर x + 1
अब
\(\lim _{x \rightarrow-1} \frac{3 x^2-2 x-5}{x+1}\) = \(\lim _{x \rightarrow-1} \frac{(x+1)(3 x-5)}{x+1}\)
= \(\lim _{x \rightarrow-1}(3 x-5)\)
= 3(1) – 5
= -3 -5
= -8
∴ \(\lim _{x \rightarrow-1} \frac{3 x^2-2 x-5}{x+1}=-8\)

प्रश्न 4.
\(\lim _{x \rightarrow 1} \frac{x^2+2 x-3}{x^2-1}\)
उत्तर :
यदि x = 1 रखने पर फलन f(x) का मूल्य \(\frac{0}{0}\) प्राप्त होगा जो अनियत है। इसलिए अंश और हर के अवयव करके x → 1 है। इसलिए
(x – 1) अंश और हर का सामान्य अवयव है।
अंश = x² + 2x – 3 = x² + 3x – x – 3 = x(x + 3) -1(x + 3) = (x – 1) (x + 3)
हर x² – 1 = (x – 1) (x + 1)

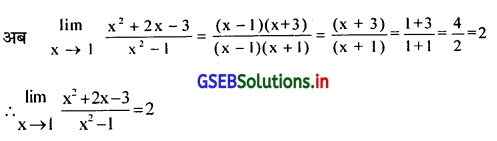
प्रश्न 5.
\(\lim _{x \rightarrow \frac{1}{2}} \frac{2 x^2+5 x-3}{4 x^2-1}\)
उत्तर :
यदि x → \(\frac{1}{2}\) रखने पर फलन f(x) का मूल्य \(\frac{0}{0}\) प्राप्त होगा जो अनियत है। इसलिए अंश और हर के अवयव करके x → \(\frac{1}{2}\) है। इसलिए (x – 1) अंश और हर का सामान्य अवयव है।
अंश = 2x² + 5x – 3 = 2x² + 6x – x – 3 = 2x (x + 3) – 1(x + 3) = (2x – 1) (x + 3)
हर 4x² – 1 = (2x – 1) (2x + 1)

प्रश्न 6.
\(\lim _{x \rightarrow-3} \frac{2 x^2+9 x+9}{2 x^2+7 x+3}\)
उत्तर :
यदि x = -3 फलन f(x) में रखने से फलन का मूल्य \(\frac{0}{0}\) प्राप्त होगा जो अनियत है। इसलिए अंश और हर का सामान्य अवयव (x + 3) है।
अंश = 2x² + 9x + 9 = 2x² + 6x +3x + 9 = 2x(x + 3) + 3 (x + 3) = (x + 3) (2x + 3)
हर = 2x² + 7x + 3 = 2x² + 6x + x + 3 = 2x(x + 3) + 1(x + 3) =(2x + 1) (x + 3)

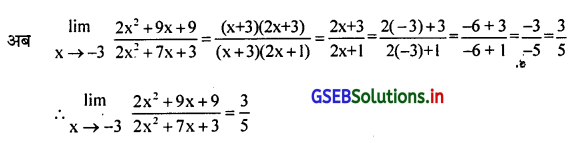
प्रश्न 7.
\(\lim _{x \rightarrow-\frac{1}{2}} \frac{2 x^2+3 x+1}{2 x^2-x-1}\)
उत्तर :
यदि x = –\(\frac {1}{2}\) फलन f(x) में रखने पर फलन का मूल्य \(\frac {0}{0}\) प्राप्त होता है। जो अनियत है इसलिए अंश और हर का सामान्य अवयव 2x + 1 है।
अंश = 2x² + 3x + 1 = 2x² + 2x + x + 1 = 2x(x + 1) + 1 (x + 1) = (2x + 1) (x + 1)
हर = 2x² – x – 1 = 2x² – 2x + x – 1 = 2x(x – 1) + (x – 1) (2x + 1) (x – 1)

प्रश्न 8.
\(\lim _{x \rightarrow-2} \frac{9 x^2+5 x-26}{5 x^2+17 x+14}\)
उत्तर :
यदि x = -2 फलन f(x) में रखने पर फलन का मूल्य \(\frac {0}{0}\) प्राप्त होता है जो अनियत है। इसलिए अंश और हर का सामान्य अवयव x + 2 है।
अंश = 9x² + 5x – 26 = 9x² + 18x – 13x – 26 = 9x (x + 2) – 13 (x + 2) = (9x -13) (x + 2)
हर = 5x² + 17x + 14 = 5x² + 10x + 7x + 14 = 5x(x + 2) + 7(x + 2)= (5x + 7) (x + 2)

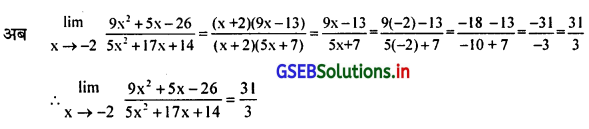
प्रश्न 9.
\(\lim _{x \rightarrow 0} \frac{1}{x}\left[\frac{5 x+14}{3 x+7}-2\right]\)
उत्तर :
यदि x = 0 फलन f(x) में रखने पर फलन का मूल्य \(\frac {0}{0}\) प्राप्त होता है जो अनियत है। इसलिए

प्रश्न 10.
\(\lim _{x \rightarrow 2}\left[\frac{2}{x-2}-\frac{4}{x^2-2 x}\right]\)
उत्तर :
यदि x = 2 फलन f(x) में रखने पर फलन का मूल्य \(\frac {0}{0}\) प्राप्त होता है। इसलिए अवयव लेकर

प्रश्न 11.
\(\lim _{x \rightarrow 0} 1+\frac{2}{3+\frac{4}{x}}\)
उत्तर :
\(\lim _{x \rightarrow 0} 1+\frac{2}{3+\frac{4}{x}}\)

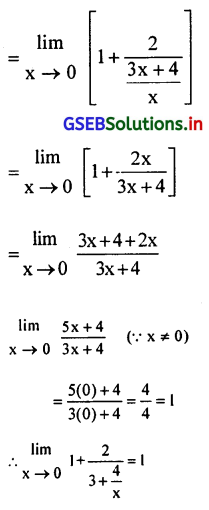
प्रश्न 12.
\(\lim _{x \rightarrow-P} \frac{x^4-p^4}{x^3+p^3}\)
उत्तर :

प्रश्न 13.
\(\lim _{x \rightarrow 3} \frac{x^6-729}{x^4-81}\)
उत्तरः

प्रश्न 14.
\(\lim _{x \rightarrow-2} \frac{x^{11}-1024}{x^5+32}\)
उत्तर :

प्रश्न 15.
\(\lim _{x \rightarrow-1} \frac{x^{2017}+1}{x^{2018}-1}\)
उत्तर :

अंश और हर को x-1 से गुणाकार करने पर

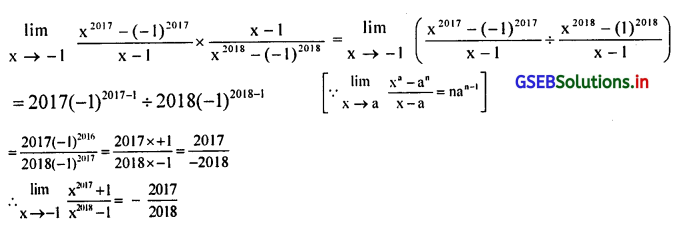
प्रश्न 16.
\(\lim _{x \rightarrow 1} \frac{x^{\frac{7}{2}}-1}{x^{\frac{3}{2}}-1}\)
उत्तर :

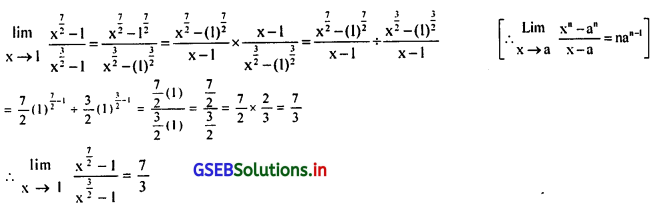
प्रश्न 17.
\(\lim _{x \rightarrow 1} \frac{\sqrt[3]{x}-1}{\sqrt{x}-1}\)
उत्तर :

विभाग – E

I. मागे अनुसार उत्तर दीजिए ।

प्रश्न 1.
यदि y = 5x + 7 हो, तो सारणी की विधि से सिद्ध कीजिए कि जब x → 2 हो तब y → 17 होगा।
उत्तर :
अब हम 2 के नजदीक की x की किंमत को लेकर निम्नानुसार सारणी बनायेंगे।

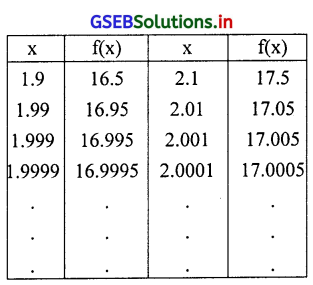
सारणी पर से स्पष्ट होता है कि जब x के मूल्यों में कमी वृद्धि करने से 2 के नजदीक लाया जाय तो f(x) का मूल्य किसी निश्चित संख्या की
ओर जाता है, लक्ष का मूल्य 17 के पास जाता है। अर्थात् x → 2 हो तब f(x) = 17 इसलिए x → 2 हो तब x → 17 होगा।

प्रश्न 2.
यदि y = \(\frac{3 x^2+16 x+16}{x+4}\) हो, तो सारणी की विधि से सिद्ध कीजिए कि जब x → -4 हो तबy → -8 होगा।
उत्तर :
f(x) = \(\frac{3 x^2+16 x+16}{x+4}\) को गणना की सरलता के लिए फलन f(x) के अंश और हर के सामान्य अवयव x + 4 को दूर करने के बाद लक्ष का
मूल्य प्राप्त कर सकते है।

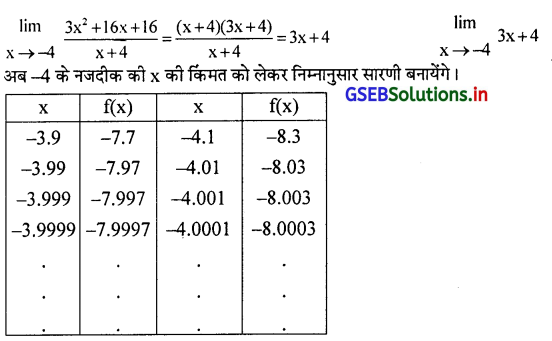
सारणी पर से स्पष्ट होता है कि जब x के मूल्यों में कमी वृद्धि करने से -4 के नजदीक लाया जाय तो f(x) का मूल्य किसी निश्चित संख्या की
ओर जाता है। लक्ष का मूल्य -8 के पास जाता है। अर्थात् x → -4 हो तब f(x) = -8 इसलिए x → -4 हो तब y → -8 होगा।

प्रश्न 3.
सारणी की विधि से सिद्ध कीजिए कि \(\lim _{x \rightarrow-1} \frac{3}{x+1}\) अस्तित्व में नहि है।
उत्तर :
यहाँ f(x) = \(\frac{3}{x+1}\) है। हम x – 1 के नजदीक की x की किंमत लेकर सारणी बनायेंगे।

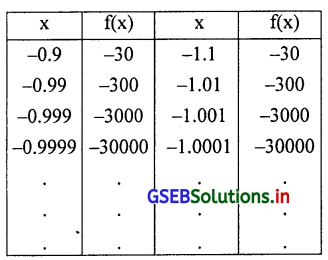
सारणी पर से स्पष्ट होता है कि जब x के मूल्य में कमी वृद्धि करके -1 के अधिक पास में लाया जाता है तब f(x) का मूल्य किसी निश्चित मूल्य की संख्या की ओर जाती नहि है; अर्थात् x → -1 हो तब f(x) किसी एक निश्चित मूल्य की अनुलक्षित नहि है। फलन अस्तित्व रखता नहि है।
∴ \(\lim _{x \rightarrow-1} \frac{3}{x+1}\) अस्तित्व रखता नहि है।

II. निम्न की सारणी की विधि से मूल्य ज्ञात कीजिए ।

प्रश्न 1.
\(\lim _{x \rightarrow 5} \frac{x^2-3 x-10}{x-5}\)
उत्तर :
f(x) = \(\frac{x^2-3 x-10}{x-5}\) को गणना की सरलता के लिए फलन f(x) के अंश और हर के सामान्य अवयव x – 5 को दूर करने पर लक्ष का मूल्य प्राप्त कर सकते है।

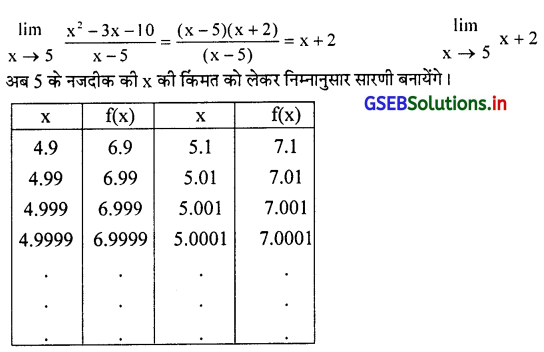
सारणी पर से स्पष्ट होता है कि जबx का मूल्य में कमी वृद्धि करके 5 के पास लाया जाता है तब f(x) का मूल्य किसी निश्चित मूल्य की ओर जाती है अर्थात् x → 5 हो तब f(x) = 7 होगा।

प्रश्न 2.
\(\lim _{x \rightarrow 1} \frac{2 x^2+3 x-5}{x-1}\)
उत्तर :
f(x) = \(\frac{2 x^2+3 x-5}{x-1}\) को गणना की सरलता के लिए फलन f(x) के अंश और हर के सामान्य अवयव x – 1 को दूर करने के बाद लक्ष का मूल्य प्राप्त कर सकते है।

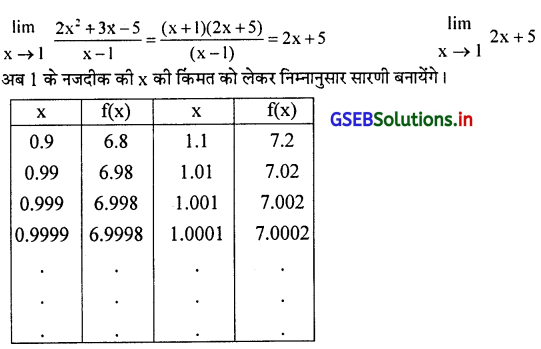
सारणी पर से स्पष्ट होता है कि जब x के मूल्य में कमी वृद्धि करके 1 के नजदीक लाया जाता है तो f(x) का मूल्य किसी निश्चित संख्या की ओर जाता है। लक्ष का मूल्य 7 के पास जाता है। अर्थात् x → 1 हो तब f(x) = 7 होगा।

प्रश्न 3.
\(\lim _{x \rightarrow-1} \frac{4 x^2+5 x+1}{x+1}\)
उत्तर :
f(x) = \(\frac{4 x^2+5 x+1}{x+1}\) को गणना की सरलता के लिए फलन f(x) के अंश और हर के सामान्य अवयव x + 1 को दूर करने के बाद लक्ष का
मूल्य प्राप्त कर सकते है।

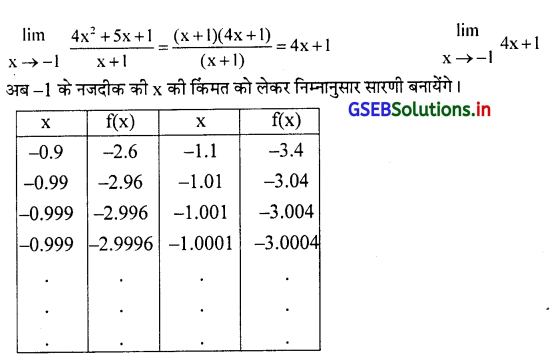
सारणी पर से स्पष्ट होता है कि जब x के मूल्यों में कमी वृद्धि करने से -1 के नदजीक लाया जाता है तो f(x) का मूल्य किसी निश्चित संख्या की ओर जाता है। लक्ष का मूल्य -3 के पास जाता है। अर्थात् x → -1 हो तब f(x) = -3 होगा।

प्रश्न 4.
\(\lim _{x \rightarrow 0} 3 x-1\)
उत्तर :
f(x) = 3x – 1 है। हम 0 के नजदीक के x के मूल्यों को लेकर निम्नानुसार सारणी बनायेंगे।

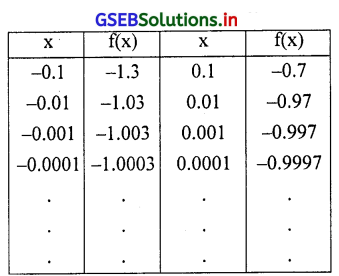
सारणी पर से स्पष्ट होता है कि जब x के मूल्य में कमी वृद्धि करके 0 के अधिक नजदीक लाया जाय तब f(x) = -1 के अधिक नजदीक जाता
है अर्थात् x → 0 हो तब f(x) = -1 होगा।

III. निम्न के मूल्य प्राप्त कीजिए ।

प्रश्न 1.
\(\lim _{h \rightarrow 0} \frac{(x+h)^7-x^7}{h}\)
उत्तर :
\(\lim _{h \rightarrow 0} \frac{(x+h)^7-x^7}{h}\)
(x + h) = t लेने पर जब h → 0 तब t → x होगा।

प्रश्न 2.
\(\lim _{x \rightarrow 0} \frac{\sqrt[10]{1+x}-1}{x}\)
उत्तर :

प्रश्न 3.
\(\lim _{x \rightarrow 0} \frac{(1+x)^n-1}{x}\)
उत्तर :

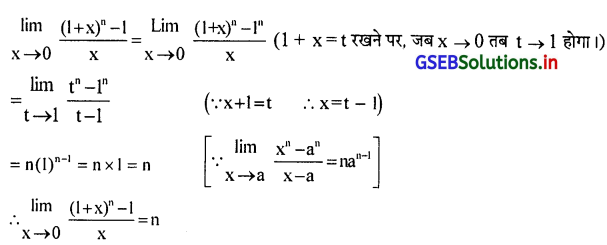
प्रश्न 4.
\(\lim _{x \rightarrow \frac{1}{2}} \frac{f(x)-f\left(\frac{1}{2}\right)}{2 x-1}\) f(x) = जहाँ x² + x – 1
उत्तर :

प्रश्न 5.
\(\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\) जहाँ f(x) = x³
उत्तर :
जहाँ f(x) = x³ ∴ f(x + h) = (x + h)³

प्रश्न 6.
\(\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\) जहाँ f(x) = x⁷
उत्तर :
f(x) = x⁷ ∴ f(x + h) = (x + h)⁷

प्रश्न 7.
\(\lim _{x \rightarrow 2} \frac{f(x)-f(2)}{x-2}\) जहाँ f(x) = \(\sqrt{x+7}\)
उत्तर :

प्रश्न 8.
\(\lim _{h \rightarrow 0} \frac{f(2+h)-f(2)}{h}\) जहाँ f(x) = 2x² + 3
उत्तर :
f(x) = 2x² + 3
f(2) = 2(2)² + 3 = 8 + 3
f(2) = 11
f(2 + h)² = 2(2 + h)² + 3
= 2(4 + 4h + h²) + 3
= 8 + 8h + 2h² + 3
= 2h² + 8h + 11

प्रश्न 9.
\(\lim _{x \rightarrow 0} \frac{f(2+x)-f(2-x)}{2 x}\) जहाँ f(x) = x²
उत्तर :
f(x) = x² ∴ f(2 + x)² – f(2 – x)²

प्रश्न 10.
\(\lim _{x \rightarrow 2} \frac{f(x)-f(2)}{x-2}\) जहाँ f(x) = x² + x
उत्तर :
f(x) = x² + x ∴ f(2)= 2² + 2 = 4 + 2 = 6