Gujarat Board Statistics Class 12 GSEB Solutions Part 1 Chapter 2 रैखिक सह-सम्बन्ध Ex 2.3 Textbook Exercise Questions and Answers.
Gujarat Board Textbook Solutions Class 12 Statistics Part 1 Chapter 2 रैखिक सह-सम्बन्ध Ex 2.3
प्रश्न 1.
दो बाजार विश्लेषक, अंतिम कुछ समय में किया गया विकास के आधार से छ कंपनीयों को निम्नानुसार क्रम दिया है ।

उत्तर :
यहाँ n = 6 और कोटि दी हुई है इसलिए कोटि सहसंबंधांक ज्ञात करने के लिए निम्नानुसार सारणी बनायेंगे ।
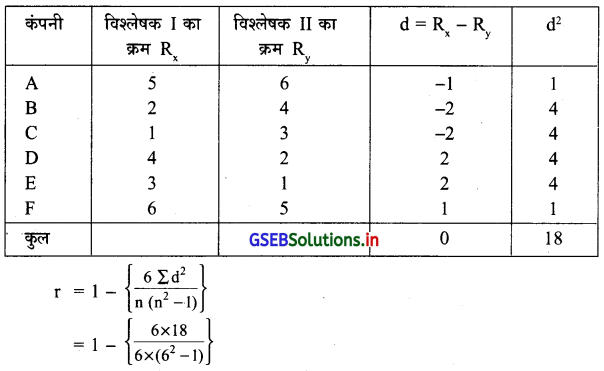
= 1 – \(\left\{\frac{108}{6 \times 35}\right\}\)
= 1 – \(\frac{108}{210}\)
= 1 – 0.51
∴ r = 0.49
प्रश्न 2.
एक न्यादर्श में दिये गये भिन्न भिन्न नौ गांव को ‘स्वच्छता अभियान’ और ‘बेटी बचाओ अभियान’ के लिए किए गए कार्यों के आधार से एक अधिकारी उसे निम्नानुसार क्रमांक देते है ।

उपयुक्त सूचना से सहसंबंध गुणांक ज्ञात कीजिए ।
उत्तर :
यहाँ n = 9 और कोटियाँ दी हुई है इसलिए कोटि सहसम्बन्ध गुणांक ज्ञात करने के लिए निम्नानुसार सारणी बनायेंगे ।
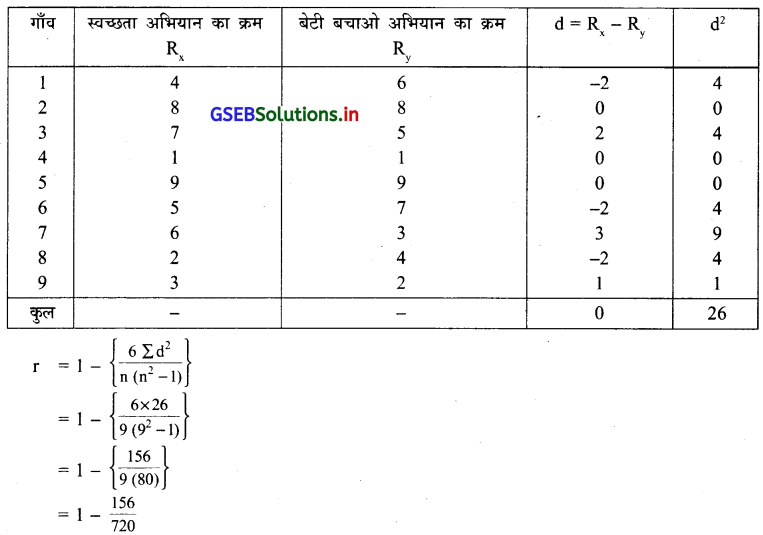
= 1 – 0.216
= 1 – 0.22
∴ r = 0.78
![]()
प्रश्न 3.
एक राज्य की टाउन प्लानिंग समिति द्वारा किया गया सर्वे पर से निम्नानुसार सूचना प्राप्त होती है ।

उपयुक्त सूचना पर से शहर की जनसंख्या और जनसंख्या वृद्धि का दर के बीच क्रमांक सहसम्बन्धाक ज्ञात कीजिए ।
उत्तर :
यहाँ n = 5 और संख्यात्मक चर दिया है इसलिए सर्वप्रथम क्रम देंगे । सबसे बड़ी संख्या से शुरूआत करके निम्नानुसार क्रम देंगे ।
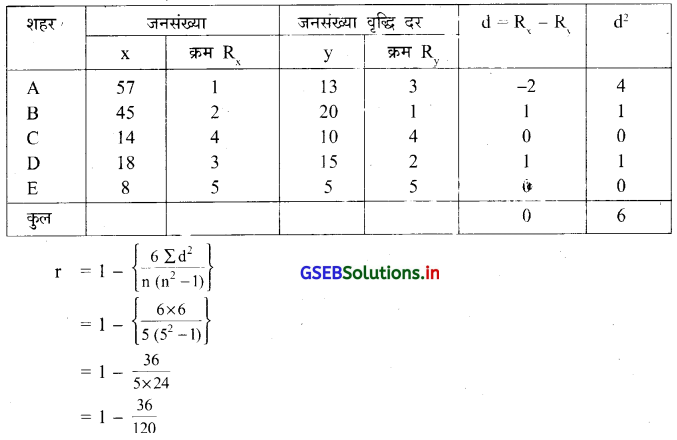
= 1 – 0.3
∴ r = 0.7
प्रश्न 4.
एक सायन्स कोलेज के विद्यार्थियों में से लिए गए दस विद्यार्थियों को एक न्यादर्श पर से निम्नानुसार सूचना प्राप्त हुई है ।

उपयुक्त सूचना पर से विद्यार्थियों द्वारा प्राप्त गणित में अंक और सांख्यिकी के बीच क्रमांक सहसंबंध गुणांक ज्ञात कीजिए ।
उत्तर :
यहाँ n = 10 और संख्यात्मक चर दिया है, इसलिए सर्वप्रथम क्रमांक देंगे । सब से बड़ी संख्या से शुरुआत करके निम्नानुसार क्रमांक प्राप्त करेंगे ।
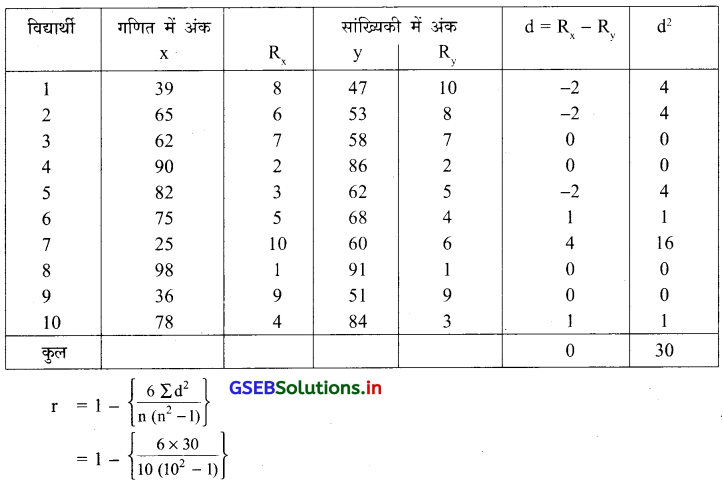
= 1 – \(\left\{\frac{180}{10 \times 99}\right\}\)
= 1 – \(\left\{\frac{180}{990}\right\}\)
= 1 – 0.18
= 0.82
∴ r = 0.82
प्रश्न 5.
निम्न दिये पति और पत्नी की ऊँचाई की सूचना पर से उसकी ऊँचाई के बीच का क्रमांक सहसम्बन्ध गुणांक ज्ञात करो ।

उत्तर :
n = 7 पत्नी की ऊँचाई के अवलोकन 154 और 162 दोनों दो बार पुनरावर्तित होती है । दोनों चर को क्रम देकर निम्नानुसार सारणी बनायेंगे ।
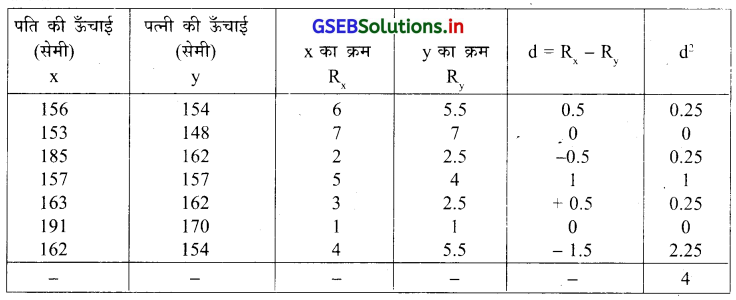
‘CF’ प्राप्त करने की गणना निम्नानुसार है ।
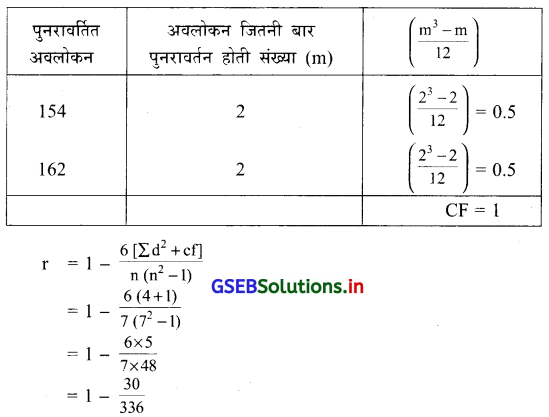
= 1 – 0.09
= 0.91
∴ r = 0.91
यहाँ r का मूल्य 1 के समीप है । इसलिए कहा जाता है के पति की उम्र और पत्नी की उम्र के बीच की क्रमांक के बीच गहेरा धन सहसंबंध है।
![]()
प्रश्न 6.
एक साक्षात्कार में उम्मीदवारों का परफोरमन्स (performance) के आधार से दो साक्षात्कार लेनेवाले व्यक्तियों द्वारा उसे निम्नानुसार अंक दिये है । दोनों व्यक्ति के मूल्यांकन पर से क्रमांक सहसंबंध गुणांक ज्ञात कीजिए ।

उत्तर :
n = 8 प्रथम व्यक्ति द्वारा दिया गया अंक 28 दो बार पुनरावर्तित होता है जबकि द्वितीय व्यक्ति द्वारा दिया गया अंक 32 तीन बार पुनरावर्तित होता है । दोनों चरों को क्रमांक देकर निम्नानुसार सारणी बनायेंगे ।
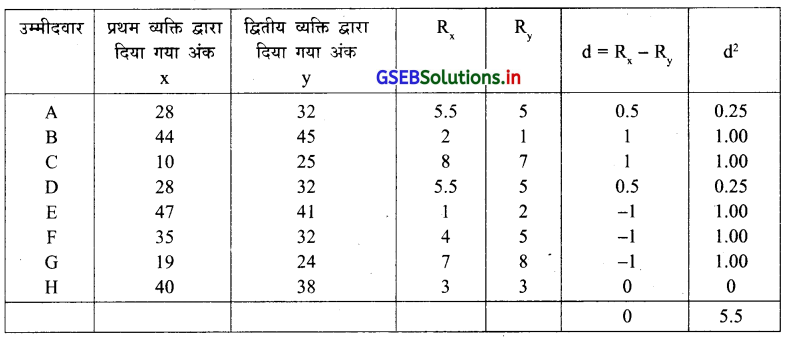
‘CF’ की गणना निम्नानुसार करेंगे ।
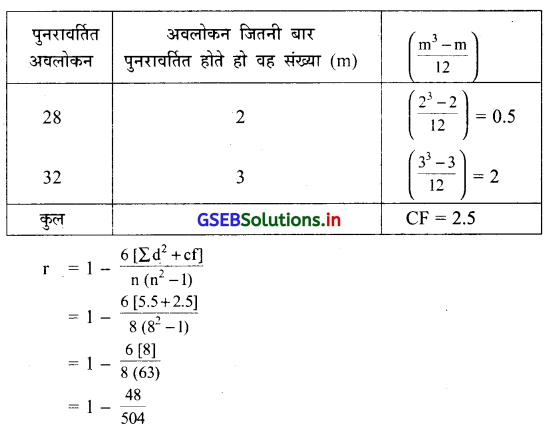
= 1 – 0.095
= 0.905
∴ r = 0.90 अथवा 0.91
दोनों व्यक्ति के मूल्यांकन के बीच गहरा धन सहसम्बन्ध है ।
प्रश्न 7.
दो निर्णायक दस स्पर्धकों को एक सौंदर्य स्पर्धा में क्रमांक देते है और उस पर से दोनों के क्रमांक के अंतर के वर्गों का योग 214 मिलता है । उस पर से क्रमांक सहसंबंध गुणांक ज्ञात कीजिए ।
उत्तर :
यहाँ n = 10 और क्रमांक के अंतर के वर्गों का योग 214 है अर्थात् Σd2 = 214 है ।

= 1 – 1.296
= 1 – 1.30
∴ r = -0.30
![]()
प्रश्न 8.
दस विद्यार्थियों द्वारा दो विषय में प्राप्त अंक पर से क्रमांक सहसंबंध गुणांक 0.5 प्राप्त हुआ है । बाद में पता चला कि । एक विद्यार्थी के क्रम का अंतर 7 होना चाहिए था । लेकिन गलती से 3 लिया गया था तो कोटि सहसंबंध की सही किंमत ज्ञात करो।
उत्तर :
यहाँ n = 10
d का गलत मान = 3
d का सही मान = 7
अब r = 1 – \(\frac{6 \sum d^2}{n\left(n^2-1\right)}\)
0.5 = 1 – \(\frac{6 \sum d^2}{10(100-1)}\)
∴ \(\frac{6 \sum d^2}{990}\) = 1 – 0.5
∴ Σd2 \(\frac{0.5 \times 990}{6}\)
∴ Σd2 = 82.5
क्रमांक का अंतर 7 के स्थान पर 3 लिया गया था इसलिए Σd2 की सही किमत निम्नानुसार प्राप्त होगी । Σd2 = 82.5 – गलत d2 + सही d2
= 82.5 – 32 + 72
= 82.5 – 9 + 49
= 82.5 + 40
= 122.5
∴ क्रमांक सहसंबंध गुणांक का मूल्य
r = 1 – \(\frac{6 \sum \mathrm{d}^2}{\mathrm{n}\left(\mathrm{n}^2-1\right)}\)
= 1 – \(\frac{6 \times 122.5}{10\left(10^2-1\right)}\)
= 1 – \(\frac{735}{10 \times 99}\)
= 1 – \(\frac{735}{990}\)
= 1 – 0.74
= 0.26
∴ r = 0.26