GSEB Solutions Class 12 Physics Chapter 1 Electric Charges and Fields

Gujarat Board GSEB Textbook Solutions Class 12 Physics Chapter 1 Electric Charges and Fields Textbook Questions and Answers, Additional Important Questions, Notes Pdf.

Gujarat Board Textbook Solutions Class 12 Physics Chapter 1 Electric Charges and Fields

GSEB Class 12 Physics Electric Charges and Fields Text Book Questions and Answers

Question 1.
What is the force between two small charged spheres having charges of 2 x 10^-7C and 3 x 10^-7C placed 30 cm apart in the air?
Solution:
q₁ = 2 x 10^-7 C, q₂ = 3 x 10^-7 C, r = 30 cm = 30 x 10^-2 m
F = 9 x 10⁹ = 9 x 10⁹ x \(\frac{2 \times 10^{-7} \times 3 \times 10^{-7}}{\left(30 \times 10^{-2}\right)^{2}}\)
= 0.06 x 10^-1 N
= 6 x 10^-3 N (repulsive)

Question 2.
The electrostatic force on a small sphere of charge 0.4 pC due to another small sphere of charge – 0.8 μC in air is 0.2 N.
(a) What is the distance between the two spheres?
(b) What is the force on the second sphere due to the first?
Solution:
q₁ = 0.4 μC = 0.4 x 10^-6 C, q₂ = – 0.8μC = – 0 .8 x 10^-6 C, F = 0.2 N

(a) F = 9 x 10⁹
r² = 9 x 10⁹ x \(\frac{\mathrm{q}_{1} \mathrm{q}_{2}}{\mathrm{~F}}\)
= \(\frac{9 \times 10^{9} \times 0.4 \times 10^{-6} \times 0.8 \times 10^{-6}}{0.2}\)
= 14.4 x 10^-3
= 144 x 10^-4m²
r = 12 x 10^-2m

(b) 0.2 N, attractive.

Question 3.
(a) Explain the meaning of the statement ‘electric charge of a body is quantised’.
(b) Why can one ignore quantisation of electric charge when dealing with macroscopic (i) e., large-scale charges?
Solution:
(a) The magnitude of charge on a proton or an electron (e = 1.6 x 10¹⁹c) is called elementary charge. Since protons and electrons are only basic charged particles in a matter, the charge on an object must be an integral multiple of ±e(1.6×10¹⁹c),
i.e. the charge possessed by an object cannot be a fraction of +e. Mathematically, the charge on any matter must be equal to q = ±ne, where n is an integer.

(b) In practice, the charge on any charged body is very large. On the other hand, the charge on an electron is very small. When electrons are added to a body (negatively charged body) or removed from a body (positively charged body), the change taking place in the total charge on the body is so small that the charge seems to be varying in a continuous manner. Therefore quantisation of electric charge can be ignored, when dealing with a large scale charged body.

Question 4.
When a glass rod is rubbed with a silk cloth, charges appear on both. A similar phenomenon is observed with many other pairs of bodies. Explain how this observation is consistent with the law of conservation of charge.
Solution:
Charge is not created or destroyed. It is merely transferred from one body to another.

Question 5.
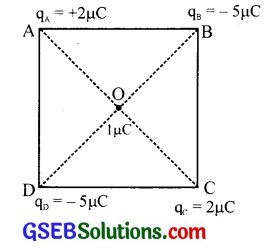
Four-point charges q_A = 2μC, q_B= – 5μC , q_C= 2μC and q_D= – 5μC are located at the corners of a square ABCD of side 10cm. What is the force on a charge of μ pC placed at the centre of the square?
Solution:
Forces on the charge 1 μC at O due to the charges – 5 μC and – 5 μC are equal and opposite. So they cancel each other. Similarly the forces due to + 2μC and + 2μC on lμC at O, also cancel each other.
So the force on a charge of 1 μC placed at the centre of the square is zero.

Question 6.
(a) An electrostatic field line is a continuous curve. That is, a field line cannot have sudden breaks. Why not?
(b) Explain why two field lines never cross each other at any point?
Solution:
(a) The tangent at a point on the electric line of force tells the direction of electric field changes from point to point. Therefore the line of force is generally, curved lines. Further, they are continuous curves and cannot have sudden breaks. For if it is so, it will indicate the absence of an electric field at the breakpoints.

(b) The tangents at a point on the line of force give the direction of the electric field at that point. If two lines of forces intersect each other at a point, then the electric field at that point will have two directions. As the same cannot be true, two lines of force will never intersect each other.

Question 7.
Two point charges q_A = 3 μC and q₃ = -3 μC are located 20 cm apart in vacuum.
(a) What is the electric field at the midpoint O of the line AB joining the two charges?
(b) If a negative test charge of magnitude 1.5 x 10^-9 C is placed at this point, what is the force experienced by the test charge?
Solution:

Question 8.
A system has two charges q_A = 2.5 x 10^-7 C and q_B = – 2.5 x 10^-7 C located at point A: (0, 0, -15 cm) and B: (0, 0, +15 cm), respectively. What are the total charge and electric dipole moment of the system?
Solution:
Total charge = Zero
p = q(2l) = 2.5 x 10^-7 x 30 x 10^-2 = 7.5 x 10^-8 Cm along z axis.

Question 9.
An electric dipole with dipole moment 4 x 10^-9 Cm is aligned at 30° with the direction of a uniform electric field of magnitude 5 x 10⁴ NC^-1 Calculate the magnitude of the torque acting on the dipole.
Solution:
p = 4 x 10^-9 Cm, θ = 30°, E = 5 x 10⁴ NC^-1
τ = pE sin θ = 4 x 10^-9 x 5 x 10⁴ x sin 30°
= 4 x 10^-9 x 5 x 10⁴ x \(\frac { 1 }{ 2 }\)
= 10 x 10^-5 Nm = 10^-4 Nm

Question 10.
A polythene piece rubbed with wool is found to have a negative charge of 3 x 10^-7C.
(a) Estimate the number of electrons transferred (from which to which?)
(b) Is there a transfer of mass from wool to polythene?
Solution:
q = 3 x 10^-7 C
(a) q = ne, n = \(\frac { q }{ e }\) = \(\frac{3 \times 10^{-7}}{1.6 \times 10^{-19}}\) ≈ 2 x 10¹² (Since polythene has negative charge, electrons are transferred from wool to polythene.)

(b) Yes. Mass transferred = n x m_e = 9.1 x 10^-3 x 2 x 10¹²
= 1.82 x 10^-18 kg

Question 11.
(a) Two insulated charged copper spheres A and B have their centres separated by a distance of 50 cm. What is the mutual force of electrostatic repulsion if the charge on each is 6.5 x 10^-7 C? The radii of A and B are negligible compared to the distance of separation.
(b) What is the force of repulsion if each sphere is charged double the above amount and the distance between them is halved?
Solution:
q₁ = q₂ = 6.5 x 10^-7C, r = 50cm = 0.5 m

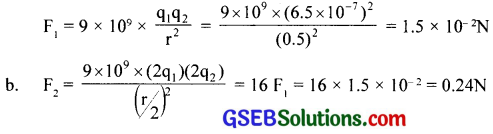
Question 12.
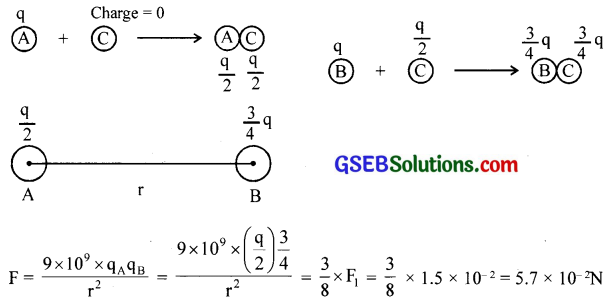
Suppose the spheres A and B in Exercise. 12 have identical sizes. A third sphere of the same size but uncharged is brought in contact with the first, then brought in contact with the second, and finally removed from both. What is the new force of repulsion between A and B?
Solution:
Charge on each of the spheres A and B is q = 6.5 x 10^-7C
When a similar but uncharged sphere C is placed in contact with sphere A, each sphere shares a charge \(\frac { q }{ 2 }\) equally.
Now when the sphere C (with charge \(\frac { q }{ 2 }\) ) is placed in contact with sphere B (with charge q), the charge is redistributed equally, so that charge on sphere B or C = \(\frac { 1 }{ 2 }\)(q + \(\frac { q }{ 2 }\)) = \(\frac { 3 }{ 4 }\)q

Question 13.
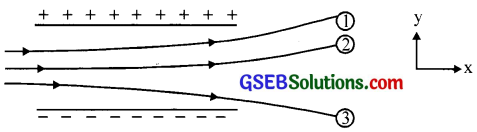
Figure below shows tracks of three charged particles in a uniform electrostatic field. Give the signs of the three charges. Which particle has the highest charge to mass ratio?

Solution:
Charges 1 and 2 are negative, charge 3 is positive.
Particle 3 has the highest charge to mass ratio.

Question 14.
Consider a uniform electric field E = 3 x 10³\(\hat { i } \) N/C.
(a) What is the flux of this field through a square of 10cm on a side whose plane is parallel to the yz plane?
(b) What is the flux through the same square if the normal to its plane makes a 60° angle with the x – axis?
Solution:
(a) E = 3 x 10³ NC^-1, r = 10 x 10^-2m
Φ = E x Area = 3 x 10³ x (10 x 10^-2)²
= 30 Nm²C^-1

(b) Φ = E x Area x cos 60° = 30 x \(\frac { 1 }{ 2 }\) = 15 Nm²C-1

Question 15.
What is the net flux of the uniform electric field of Exercise.15 through a cube of side 20 cm oriented so that its faces are parallel to the coordinate planes?
Solution:
Zero. The number of lines entering the cube is the same as the number of lines leaving the cube.

Question 16.
Careful measurement of the electric field at the surface of a black box indicates that the net outward flux through the surface of the box is 8.0 x 10³ Nm²/C.
(a) What is the net charge inside the box?
(b) If the net outward flux through the surface of the box were zero, could you conclude that there were no charges inside the box? Why or why not?
(a) Φ = \(\frac{\mathrm{q}}{\varepsilon_{0}}\)
q = Φ x \(\varepsilon_{0}\)
= 8 x 10³ x 8.85 x 10^-12
= 0.07 μC

(b) If the net outward flux through the surface of the box is zero, it cannot be concluded that there is no charge inside the box. There may be an equal amount of positive and negative charges inside the box. Therefore, if the net outward flux is zero, we cannot conclude that the charge inside the box is zero. One can only say that the net charge inside the box is zero.

Question 17.
A point charge +10 μC is at a distance 5 cm directly above the centre of a square of side 10 cm, as shown in figure. What is the magnitude of the electric flux through the square? (Hint: Think of the square as one face of a cube with edge 10cm)

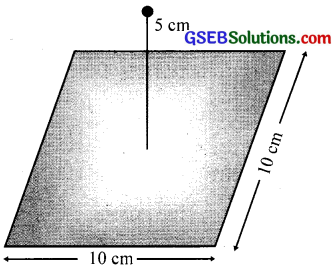
Solution:

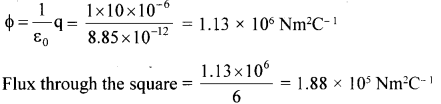
Question 18.
A point charge of 2.0 pC is at the centre of a cubic Gaussian surface 9.0 cm on edge. What is the net electric flux through the surface?
Solution:
\(\frac{2.0 \times 10^{-6}}{\varepsilon_{0}}\) = \(\frac{2.0 \times 10^{-6}}{8.85 \times 10^{-12}}\) = 2.26 x 10^-5Nm^-1

Question 19.
A point charge causes an electric flux of -1.0 x 10³ Nm²/C to pass through a spherical Gaussian surface of 10.0 cm radius centered on the charge.
(a) If the radius of the Gaussian surface were doubled, how much flux would pass through the surface?
(b) What is the value of the point charge?
Solution:
(a) If the radius of the gaussian surface is doubled, the electric flux through the new surface will still remain the same i.e. -1 x 10³Nm²C^-1 This is because the same charge is enclosed by the gaussian surface in the two cases.

(b) Φ = \(\frac{\mathrm{q}}{\varepsilon_{0}}\), q = \(\varepsilon_{0}\) Φ = 8.85 x 10^-12 x – 1 x 10³ = – 8.85 x 10^-9C

Question 20.
A conducting sphere of radius 10 cm has an unknown charge. If the electric field 20 cm from the centre of the sphere is 1.5 x 10³N/C and points radially inward, what is the net charge on the sphere?
Solution:

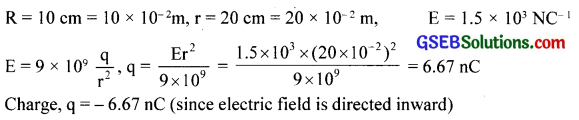
Question 21.
A uniformly charged conducting sphere of 2.4 m diameter has a surface charge density of 80.0 μC /m².
(a) Find the charge on the sphere.
(b) What is the total electric flux leaving the surface of the sphere?
Solution:
r = \(\frac { 2.4 }{ 2 }\) = 1.2m, σ = 80µCm^-2 = 80 x 10^-6

Question 22.
An infinite line charge produces a field of 9 x 10⁴ N/C at a distance of 2cm. Calculate the linear charge density.
Solution:
E = 9 x 10⁴ NC^-1, r = 2 cm = 2 x 10^-2m
E = 9 x 10⁹ x \(\frac { 2λ }{ 2 }\)
λ = \(\frac{\mathrm{Er}}{9 \times 10^{9} \times 2}\) = \(\frac{9 \times 10^{4} \times 2 \times 10^{-2}}{9 \times 10^{9} \times 2}\) = 0.1µC/m

Question 23.
Two large, thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite sign and of magnitude 17.0 x 10^-11 C/m². What is E
(a) in the outer region of the first plate, (b) in the outer region of the second plate, and (c) between the plates?
Solution:

Question 24.
An oil drop of 12 excess electrons is held stationary under a constant electric field of 2.55 x 10^-4 NC^-1 in Millikan’s oil drop experiment. The density of the oil is 1.26g cm^-3. Estimate the radius of the drop, (g = 9.81 ms^-2; e = 1.60 x 10^-19 C).
Solution:
n= 12, e= 1.6 x 10^-19C, r = ?. E = 2.55 x 10⁴NC^-1
d = 1.26 g cm^-3 = 1.26 x 10³ kgm^-3
Weight of the drop = Force due to electric field

Question 25.
Which among the curves shown in figure cannot possibly represent electrostatic field lines?
Solution:

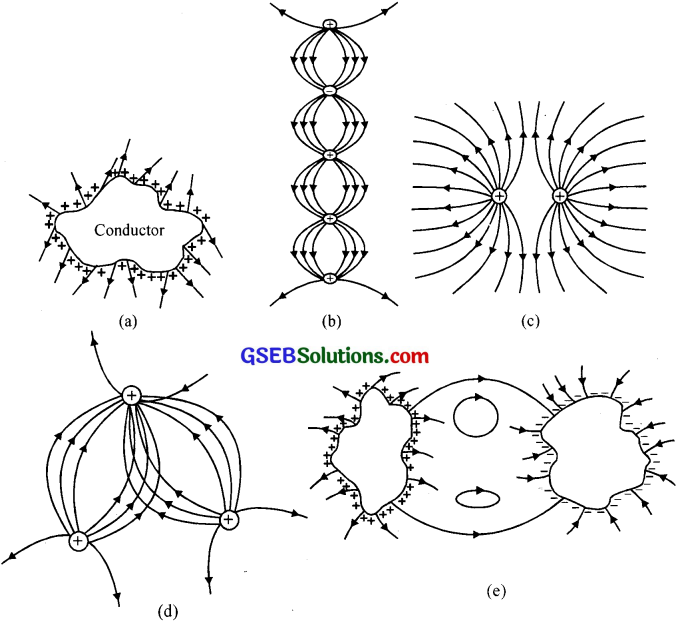
Only (c) is right; the rest cannot represent electrostatic field lines, (a) is wrong because field lines must be normal to a conductor, (b) is wrong because field lines cannot start from a negative charge, (d) is wrong because field lines cannot intersect each other, (e) is wrong because electrostatic field lines cannot form closed loops.

Question 26.
In a certain region of space, the electric field is along the z-direction throughout. The magnitude of the electric field is, however, not constant but increases uniformly along the positive z-direction, at the rate of 10⁵NC^-1 per metre. What are the force and torque experienced by a system having a total dipole moment equal to 10^-7Cm in the negative z-direction?
Solution:

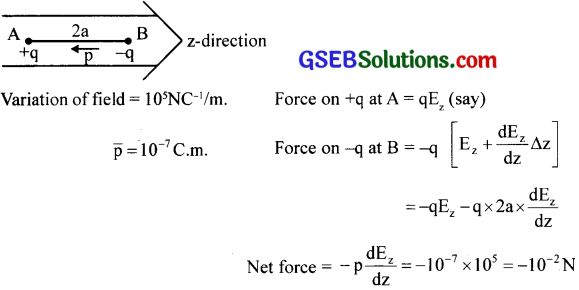
Negative sign shows that the force is against the field.
Torque, τ = \(\bar { P } \) x \(\bar { E } \) = PEsinθ \(\bar { n } \) , since θ = π , sin π = 0, hence torque is zero.

Question 27.
(a) A conductor A with a cavity as shown in the figure is given a charge Q. Show that the entire charge must appear on the outer surface of the conductor.
(b) Another conductor B with charge q is inserted into the cavity keeping B insulated from (a) Show that the total charge on the outside surface of A is Q + q [figure (b)].
(c) A sensitive instrument is to be shielded from the strong electrostatic fields in its environment. Suggest a possible way.

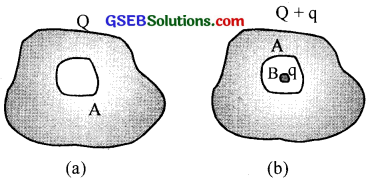
(a) Imagine a Gaussian surface within the conductor and enclosing the cavity. If some charge is present within, the corresponding electric field should be present. But the field inside a conductor is zero. Hence there cannot be charged inside the Gaussian surface. The same argument can be extended just upto the surface. Therefore the whole charge Q will be shifted to the surface.

(b) The source charge, q inside produces induced -ve charge on the inner wall of the cavity leaving that much +ve charge to the surface. Hence total surface charge is (Q + q).

(c) The instrument should be kept within a metal case.

Question 28.
Obtain the formula for the electric field due to a long thin wire of uniform linear charge density λ without using Gauss’s law. [Hint: Use Coulomb’s law directly and evaluate the necessary integral]
Solution:

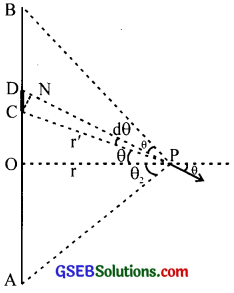
AB is the straight line of uniform charge density λ.

Question 29.
It is now believed that protons and neutrons (which constitute nuclei of ordinary matter) are themselves built out of more elementary units called quarks. A proton and a neutron consist of three quarks each. Two types of quarks, the so-called ‘up quark (denoted by u) of charge + \(\frac { 2 }{ 3 }\)e, and the ‘down’ quark (denoted by d) of charge \(\frac { -1 }{ 3 }\) have also been found which give rise to different unusual varieties of matter.) Suggest a possible quark composition of a proton and neutron.
Solution:
p; uud, n; udd

GSEB Class 12 Physics Electric Charges and Fields Additional Important Questions and Answers

Question 1.
A glass rod rubbed with silk is brought close to tw>o uncharged spheres in contact with each other inducing charges on them as shown in the figure. What happens when
(a) the spheres are slightly separated.
(b) the glass rod is subsequently removed.
(c) the spheres are separated far apart.

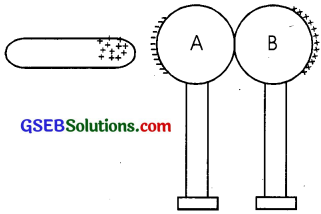
Answer:
(a) Charges remain as such, with little displacement on their spheres.
(b) The charges are displaced so as to face each other on the nearer side.
(c) Uniform distribution takes place.

Question 2.
Although ordinary rubber is an insulator, the special rubber tyres of aircraft are made slightly conducting. Explain why.
Answer:
The aircraft while in motion gets charged due to atmospheric air friction. The continuous charging may raise the sharp conducting metal parts to discharge state which will cause spark and even explosion. If the tyres are made conducting, charge will be collected to the tyres and at the time of launching it may safely get discharged to the ground.

Question 3.
Vehicles carrying inflammable material usually have metallic ropes touching the ground during motion. Why?
Answer:
Moving vehicles get charged due to friction. This will produce sparking and the inflammable material may catch fire. To avoid these metallic chains are used. Through these chains the charges are transferred to the earth.

Question 4.
Is coulomb a very big unit of charge?
Answer:
Yes. The force of repulsion between two one coulomb charges placed one metre apart in air or vacuum is 9 x 10⁹ N, which is enormous.

Question 5.
The electric field can be studied in terms of electric field intensity.
(a) What is an electric field?
(b) Define electric field strength. Give its unit and dimensional formula
(c) Who introduced the concept of electric field?
(d) Is the electric field a scalar quantity or a vector quantity?
Answer:
(a) Electric field refers to the region surrounding a charge where its influence is felt. Space where charges or charged bodies electrically interact is called an electric field.

(b) Intensity of electric field or electric field strength at any point is defined as the electric force per unit positive charge placed at that point.
Unit: NC^-1; Dimension : [M’L’T^-3A^-1]

(c) Micheal Faraday

(d) A vector quantity

Question 6.
Show mathematically that the electric field strength due to a short electric dipole at a distance ‘r’ along its axis is twice that at the same distance along its equatorial axis.
Answer:

Question 7.
What is the total force acting on the dipole?
Answer:
Zero

Question 8.
What is the effect of keeping the dipole in the field?
Answer:
If the dipole is placed parallel to the field, it is in stable equilibrium, and if placed antiparallel, it is in the unstable equilibrium. If it is inclined, it is subjected to torque and hence rotation.

Question 9.
What happens if the field is not uniform?
Answer:
There will be both translational and rotational motions.

Question 10.
The following four insulating spheres contain magnet, dipole, proton, and neutron. Pick the odd one out of the following based on the net flux.

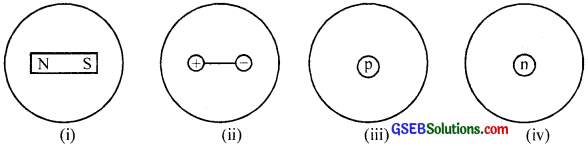
In case (iii), the net flux is not zero

Question 11.
How does the electric field (E) vary with distance (r) in the following cases?
(i) Uniformly charged spherical shell
(ii) Uniformly charged solid sphere.
(iii) Uniformly charged plane sheet of large size.
Also, plot a graph between E and r in each case.
Answer:
(i) Outside ∝\(\frac { 1 }{ { r }^{ 2 } }\), on surface = \(\frac { 1 }{ { r }^{ 2 } }\), inside = zero
(ii) On the surface = \(\frac { 1 }{ { r }^{ 2 } }\), inside ∝ r
(iii) Constant, E =\(\frac{\sigma}{2 \varepsilon_{0}}\), independent of r

Question 12.
Give the expression for the time period of oscillation of an electric dipole in a uniform electric field.
Answer:
Time period, T = 2π\(\sqrt{\frac{1}{\mathrm{pE}}}\)
where, I – moment of inertia of the dipole
p – dipole moment
E – Electric field strength

Question 13.
A pendulum bob of mass 40 mg and carrying a charge of 2 x 10^-5C is at rest in a horizontal uniform electric field of 2 x 10⁴NC^-1. Find the tension in the string of the pendulum and the angle it makes with the vertical.
Answer:
The various forces acting on the bob are

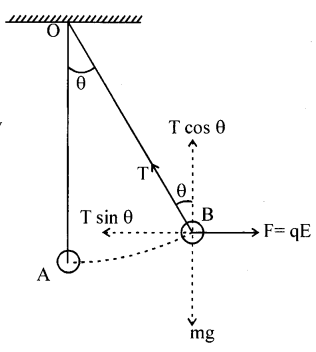
(i) Weight (mg) of the bob acting vertically down
(i) Tension (T) developed in the string and
(iii) Electrostatic force (F=qE) acting horizontally
for the bob to be in equilibrium.
For the bob to be in equilibrium, T cos G = mg
and T sinθ = qE

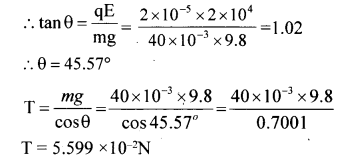
Question 14.
A charge Q is fixed at each of two opposite corners of a square. A charge q is placed at each of the other two corners. If the net electrostatic force on each Q is zero, what is Q in terms of q?
Answer:

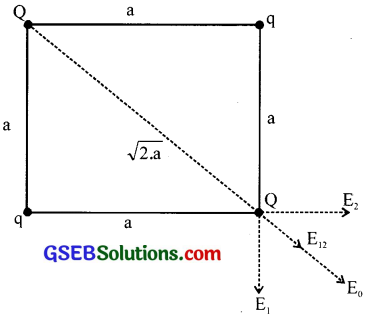
Let ‘a’ be the length of the side of the square. Force on Q due to the other charge

Question 15.
It is safe to sit inside a vehicle, whenever there is lightning and thunder. Why?
Answer:
Electrostatic screening of conducting surface.

Question 16.
Equipment very sensitive to electric field is to be transferred from one point to another. What precautions you will do?
Answer:
It should be kept in a metal cage.

Question 17.
An electric flux of – 6 x 10³ Nm²/C passes normally through a spherical Gaussian surface of a radius of 10 cm, due to a point of charge placed at the centre.
(i) What is the charge enclosed by the Gaussian surface?
(ii) If the radius of the Gaussian surface is doubled, how much flux will pass through the surface?
Answer:
(i) φ = – 6 x 10³Nm²C^-1
By Gauss’s theorem, φ = \(\frac{\mathrm{q}}{\varepsilon_{0}}\)
q= \(\varepsilon_{0}\) x φ = 8.85 x 1o^-12 x – 6 x 10³ = – 5.31 x 10^-8C

(ii) Same (- 6 x 10³ Nm²C^-1)