GSEB Class 10 Maths Notes Chapter 12 વર્તુળ સંબંધિત ક્ષેત્રફળ

This GSEB Class 10 Maths Notes Chapter 12 વર્તુળ સંબંધિત ક્ષેત્રફળ covers all the important topics and concepts as mentioned in the chapter.

વર્તુળ સંબંધિત ક્ષેત્રફળ Class 10 GSEB Notes

→ પ્રાસ્તાવિક આપણા દૈનિક જીવનમાં આપણે એક અથવા બીજી રીતે વર્તુળના આકારને સંબંધિત ઘણી વસ્તુઓના પરિચયમાં આવીએ છીએ. જેવી કે, સાઇકલનું પૈડું, ગોળાકાર કેક, ગટરનું ઢાંકણું વગેરે. ઘણી વખત આપણે તે વસ્તુઓની પરિમિતિ તથા ક્ષેત્રફળ શોધવું પડે છે. આ પ્રકરણમાં આપણે આ પ્રકારના પ્રશ્નોના ઉકેલ શોધવાનું શીખીશું.

→ વર્તુળની પરિમિતિ અને ક્ષેત્રફળ (Circumference and area of a circle) : વર્તુળની પરિમિતિને વર્તુળનો પરિઘ કહે છે. આપણે જાણીએ છીએ કે, વર્તુળના પરિઘ અને વ્યાસનો ગુણોત્તર અચળ છે. જેને ગ્રીક અક્ષર ૪ (વંચાય પાઈ) દ્વારા દર્શાવાય છે.

→ π એક અસંમેય સંખ્યા છે. સામાન્યતઃ πની આશરે કિંમત (આસન મૂલ્ય) તરીકે \(\frac{22}{7}\) અથવા 3.14નો ઉપયોગ થાય છે. જો કોઈ અન્ય ઉલ્લેખ ન કર્યો હોય, તો સમગ્ર પ્રકરણમાં
આપણે π = \(\frac{22}{7}\) નો ઉપયોગ કરીશું.

→ વર્તુળનો પરિઘ = πd, જ્યાં d એ વર્તુળનો વ્યાસ છે.

→ વર્તુળનો પરિઘ = 2πr, જ્યાં એ વર્તુળની ત્રિજ્યા છે.

→ વર્તુળનું ક્ષેત્રફળ = \(\frac{\pi d^{2}}{4}\) જ્યાં એ વર્તુળનો વ્યાસ છે.

→ વર્તુળનું ક્ષેત્રફળ = πr², જ્યાં એ વર્તુળની ત્રિજ્યા છે.

→ અર્ધવર્તુળ (semicircle): વર્તુળનો કોઈ પણ વ્યાસ વર્તુળનું બે સમાન ભાગમાં વિભાજન કરે છે. આ દરેક ભાગને અર્ધવર્તુળ કહે છે.

→ r ત્રિજ્યાવાળા અર્ધવર્તુળ માટે, અર્ધવર્તુળની પરિમિતિ = \(\frac{1}{2}\)(2πr) + 2r
= πr + 2r.

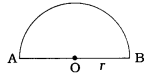
અર્ધવર્તુળનું ક્ષેત્રફળ = \(\frac{1}{2}\) πr²

→ વર્તુળનું ચતુર્ભાશ (ઉuadrant of a circle) : વર્તુળના બે પરસ્પર લંબ હોય તેવા વ્યાસ દ્વારા વર્તુળનું ચાર સમાન ભાગમાં વિભાજન થાય છે. આ દરેક ભાગને વર્તુળનું ચતુર્થાંશ કહેવાય છે.

r ત્રિજ્યા ધરાવતાં વર્તુળના ચતુર્ભાશ માટે,
વર્તુળના ચતુર્થાશની પરિમિતિ = \(\frac{1}{2}\)(2πr) + 2r
= \(\frac{πr}{2}\)(2πr) + 2r

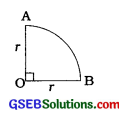
વર્તુળના ચતુર્થાશનું ક્ષેત્રફળ = \(\frac{1}{4}\)πr²

→ કંકણાકાર(Circular ring)નું ક્ષેત્રફળ : બે સમકેન્દ્રી વર્તુળો – C₁ અને C₂ વચ્ચે ઘેરાયેલા ભાગને કંકણાકાર કહે છે.

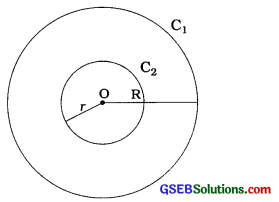
ધારો કે, O કેન્દ્રવાળાં બે સમકેન્દ્રી વર્તુળો C₁ અને C₂ની ત્રિજ્યા અનુક્રમે R અને r (R > r) છે.
કંકણાકારનું ક્ષેત્રફળ = વર્તુળ C₁ નું ક્ષેત્રફળ -વર્તુળ C₂ નું ક્ષેત્રફળ
= πR² – πr²
= πR(R² – r²).
= 1 (R + r)(R – r)

અહીં, R – r એ કંકણાકારની પહોળાઈ દર્શાવે છે.

→ વર્તુળાકાર પૈડાંએ એક પરિભ્રમણમાં કાપેલ અંતર
= પૈડાંનો પરિઘ
= 2πr, જ્યાં એ પૈડાંની ત્રિજ્યા છે.

→ ઝડપના એકમનું રૂપાંતરણઃ

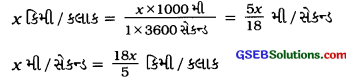
→ વર્તુળના વૃત્તાંશ અને વૃત્તખંડનું ક્ષેત્રફળ ક વર્તુળનું ચાપ (Arc of a circle) : વર્તુળ પરનાં બે બિંદુઓ વચ્ચેના વર્તુળના ભાગને વર્તુળનું ચાપ કહે છે. ચાપની લંબાઈને l દ્વારા દર્શાવાય છે.

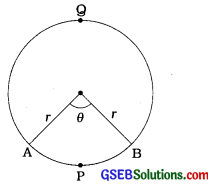
→ લઘુચાપ (Minor arc) : વર્તુળના જે ચાપની લંબાઈ વર્તુળના પરિઘના અડધાથી ઓછી હોય તેને લઘુચાપ કહે છે. આપેલ આકૃતિમાં APB લઘુચાપ છે.

→ ગુરુચાપ (Major arc) : વર્તુળના જે ચાપની લંબાઈ વર્તુળના પરિઘના અડધાથી વધારે હોય તેને ગુરુચાપ કહે છે. આપેલ આકૃતિમાં AQB ગુરુચાપ છે.

→ અર્ધવર્તુળ ચાપ (Semicircular arc) : વર્તુળના જે ચાપની લંબાઈ વર્તુળના પરિઘના અડધા જેટલી હોય તેને અર્ધવર્તુળ ચાપ કહે છે.

→ સૂત્રઃ જો લઘુચાપ APBનાં અંત્યબિંદુઓ A અને Bમાંથી દોરેલ ત્રિજ્યાઓ વચ્ચેના ખૂણાનું માપ 9 હોય અને વર્તુળની ત્રિજ્યા r હોય, તો લઘુચાપ APBની લંબાઈ = \(\frac{\theta}{360}\) × 2πr અને ગુરુચાપ AGBની લંબાઈ = પરિઘ – લઘુચાપની લંબાઈ
= 2πr – \(\frac{\theta}{360}\) × 2πr

→ લઘુચાપની લંબાઈ + ગુરુચાપની લંબાઈ = વર્તુળનો પરિઘ

→ વૃત્તાંશ (Sector): ત્રિજ્યા અને વર્તુળના ચાપ વચ્ચે ઘેરાયેલા પ્રદેશ(અથવા ભાગ)ને વર્તુળનો વૃત્તાંશ કહે છે.

→ લઘુવૃત્તાંશ (Minor sector): જે વૃત્તાંશને સંગત ચાપ લઘુચાપ હોય તે વૃત્તાંશને લઘુવૃત્તાંશ કહે છે. આપેલ આકૃતિમાં છાયાંતિ પ્રદેશ OAPB લઘુવૃત્તાંશ દર્શાવે છે.

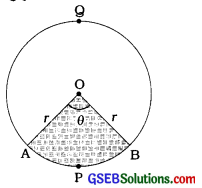
→ ગુરુવૃત્તાંશ (Major sectory): જે વૃત્તાંશને સંગત ચાપ ગુરુચાપ હોય તે વૃત્તાંશને ગુરુવૃત્તાંશ કહે છે. આપેલ આકૃતિમાં બિનછાયાંકિત પ્રદેશ OBBA ગુરુવૃત્તાંશ દર્શાવે છે.

→ વૃત્તાંશનો ખૂણો (Angle of a sector): કોઈ પણ વૃત્તાંશને સંગત ચાપ વર્તુળના કેન્દ્ર આગળ જે ખૂણો આંતરે તે ખૂણાને વૃત્તાંશનો ખૂણો કહે છે. આપેલ આકૃતિમાં લઘુવૃત્તાંશ OAPBનો ખૂણો θ છે અને ગુરુવૃત્તાંશ OBQAનો ખૂણો 360° – θ છે. સ્વાભાવિક છે કે લઘુવૃત્તાંશનો ખૂણો 180° કરતાં ઓછો હોય અને ગુરુવૃત્તાંશનો ખૂણો 180° કરતાં અધિક હોય.

→ સૂત્રઃ જો r ત્રિજ્યાવાળા વર્તુળના કોઈ લઘુવૃત્તાંશના ખૂણાનું અંશમાપ 9 હોય, તો લઘુવૃત્તાંશનું ક્ષેત્રફળ = \(\frac{\theta}{360}\) × πr² અને ગુરુવૃત્તાંશનું ક્ષેત્રફળ
= વર્તુળનું ક્ષેત્રફળ – સંગત લઘુવૃત્તાંશનું ક્ષેત્રફળ
= πr² – \(\frac{\theta}{360}\) × πr²

→ ગુરુવૃત્તાંશનું ક્ષેત્રફળ \(\frac{360-\theta}{360}\) × πr² દ્વારા પણ મેળવી શકાય.

→ લઘુવૃત્તાંશ OAPBની પરિમિતિ
= OA + OB + ચાપ ABની લંખાઈ
= r + l + l
= 2r + \(\frac{\theta}{360}\) ×2πr

→ વર્તુળનો વૃત્તખંડ (Segment of a circle): જીવા અને તેના બંનેમાંથી કોઈ પણ ચાપ વચ્ચેના પ્રદેશને વર્તુળાકાર પ્રદેશનો વૃત્તખંડ અથવા સરળ રીતે વર્તુળનો વૃત્તખંડ કહે છે. બીજા શબ્દોમાં, વર્તુળની કોઈ પણ ચાપ અને તેનાં અંત્યબિંદુઓને જોડતી જીવાથી ઘેરાયેલા પ્રદેશને વર્તુળનું વૃત્તખંડ કહે છે.

→ લઘુવૃત્તખંડ (Minor segment) : જે વૃત્તખંડને સંગત ચાપ લઘુચાપ હોય, તે વૃત્તખંડને લઘુવૃત્તખંડ કહે છે. બીજા શબ્દોમાં, અર્ધવર્તુળથી નાના વૃત્તખંડને લઘુવૃત્તખંડ કહે છે. આપેલ આકૃતિમાં છાયાંકિત પ્રદેશ A લઘુવૃત્તખંડ APB દર્શાવે છે.

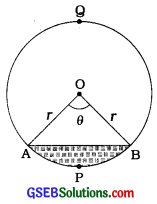
→ ગુરુવૃત્તખંડ (Major segment): જે વૃત્તખંડને સંગત ચાપ ગુરુચાપ હોય, તે વૃત્તખંડને ગુરુવૃત્તખંડ કહે છે. બીજા શબ્દોમાં, અર્ધવર્તુળથી મોટા વૃત્તખંડને ગુરુવૃત્તખંડ કહે છે. આપેલ આકૃતિમાં બિનછાયાંકિત પ્રદેશ ગુરુવૃત્તખંડ BQA દર્શાવે છે.

→ સૂત્રઃ
લઘુવૃત્તખંડનું ક્ષેત્રફળ = લઘુવૃત્તાંશનું ક્ષેત્રફળ – સંગત ત્રિજ્યા અને જીવા દ્વારા બનતા ત્રિકોણનું ક્ષેત્રફળ

આપેલ આકૃતિમાં,
લઘુવૃત્તખંડ APBનું ક્ષેત્રફળ
= લઘુવૃત્તાંશ OAPBનું ક્ષેત્રફળ – ΔGABનું ક્ષેત્રફળ ગુરુવૃત્તખંડનું ક્ષેત્રફળ
= વર્તુળનું ક્ષેત્રફળ – સંગત લઘુવૃત્તખંડનું ક્ષેત્રફળ

અહીં, ΔDABનું ક્ષેત્રફળ (sin\(\frac{\theta}{2}\) cos\(\frac{\theta}{2}\)r²) દ્વારા પણ મેળવી શકાય.
આથી લધુત્તખંડનું ક્ષેત્રફળ = \(\frac{\theta}{360}\)πr² – sin\(\frac{\theta}{2}\) cos\(\frac{\theta}{2}\)r²
= {\(\frac{\pi \theta}{360}\) – sin\(\frac{\theta}{2}\) cos\(\frac{\theta}{2}\)}r²

→ લઘુવૃત્તાંશનું ક્ષેત્રફળ

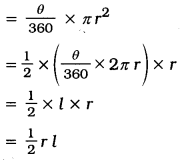
જ્યાં, I એ સંગત ચાપની લંબાઈ છે.

નોંધઃ જો સ્પષ્ટતા ન કરી હોય, તો આપણે વૃત્તખંડ અને વૃત્તાંશના અર્થ અનુક્રમે “લઘુવૃત્તખંડ’ અને લઘુવૃત્તાંશ’ કરીશું.

→ સંયોજિત સમતલીય આકૃતિઓનું ક્ષેત્રફળ : અત્યાર સુધી આપણે ભિન્ન ભિન્ન આકૃતિઓના ક્ષેત્રફળની અલગ અલગ રીતે ગણતરી કરી છે. હવે આપણે ચોરસ, લંબચોરસ, વર્તુળ, અર્ધવર્તુળ, વૃત્તાંશ, વૃત્તખંડ, ત્રિકોણ વગેરે દ્વારા બનતી સંયોજિત આકૃતિઓનું ક્ષેત્રફળની ગણતરી કરીશું

→ વર્તુળનો પરિઘ = 2πr

→ વર્તુળનું ક્ષેત્રફળ = πr²

→ બહારની ત્રિજ્યા r₁ અને અંદરની ત્રિજ્યા r₂ હોય તેવા કંકણાકારનું ક્ષેત્રફળ = π(r₁ + r₂) (r₁ – r₂).

→ r ત્રિજ્યાવાળા અને છ માપનો ખૂણો બનાવતા વર્તુળના વૃત્તાંશના ચાપની લંબાઈ 18 \(\frac{\theta}{360}\) × 2πr છે.

→ r ત્રિજ્યાવાળા અને માપનો ખૂણો બનાવતા વર્તુળના વૃત્તાંશનું ક્ષેત્રફળ \(\frac{\theta}{360}\) × πr² છે.

→ r ત્રિજ્યાવાળા વર્તુળની 1 લંબાઈવાળી ચાપ દ્વારા બનતા વૃત્તાંશનું ક્ષેત્રફળ = \(\frac{1}{2}\) rl.

→ વર્તુળના લઘુવૃત્તખંડનું ક્ષેત્રફળ = અનુરૂપ વૃત્તાંશનું ક્ષેત્રફળ – અનુરૂપ ત્રિકોણનું ક્ષેત્રફળ

→ વર્તુળના ગુરુવૃત્તખંડનું ક્ષેત્રફળ = વર્તુળનું ક્ષેત્રફળ – અનુરૂપ લઘુવૃત્તખંડનું ક્ષેત્રફળ