GSEB Class 10 Maths Notes Chapter 13 Surface Areas and Volumes

This GSEB Class 10 Maths Notes Chapter 13 Surface Areas and Volumes covers all the important topics and concepts as mentioned in the chapter.

Surface Areas and Volumes Class 10 GSEB Notes

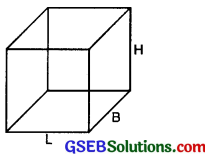
Surface Areas and Volumes Cuboid:
Volume of cuboid = LBH
Total surface area = 2[LB + BH + HL]
Lateral surface area = 2[L + B]H

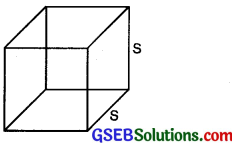
Cube:
Side of each side of cube = x
Volume of cube = (side)³
Lateral surface area = 6 (side)²
Total surface area of cube = 4 (side)²

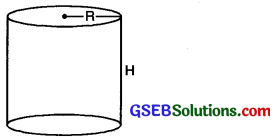
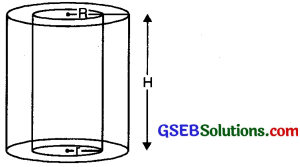
Right circular cylinder:
Volume of cylinder = πR²H
Curved surface area of cylinder =2πRH
Total surface area of cylinder
=2πR[R+H]

Hollow Cylinder:
Volume of material = π [R² – r²] H
Curved surface area = 2πH [R + r]
Area of Base = π [R² + r²]

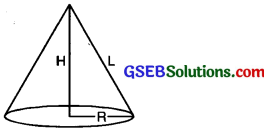
Right Circular cone:
Area of base = πR²
Curved surface area = πRL
Total surface area = πR² + πRL
= πR [R + L]
Volume of Cone = \(\frac{1}{3}\)πRH
L = \(\sqrt{\mathrm{R}^{2}+\mathrm{H}^{2}}\)

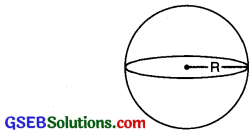
Sphere:
Volume of sphere = \(\frac{4}{3}\)πR³
Formula for finding Surface area of sphere = 4πR².

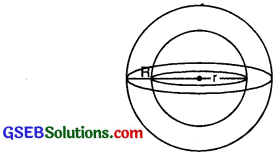
Hollow sphere:
Volume of hollow sphere = \(\frac{4}{3}\)π [R -r ]

Hemi-sphere:
Volume of hemi sphere = \(\frac{2}{3}\)πR
Curved surface area of hemi-sphere
= 2πr²
Total surface of a hemi-sphere = 3πr².

Surface Area of a Combination of Solids
In our daily life, we saw various interesting designs, where two or more standard soild figures are combined to form a new solid. In such types of problems, firstly, we divide it into different known solids. So, we find surface area of each solid separately and then adding all these areas, we find area of required combined solid.

Volume of a Combination of Solids
In Our daily life, we saw various interesting designs, where two or more standard solid figures are combined to form a new solid. In such type of problems, firstly, we divide it into different known solids. So, we find volume of each solid separately and then adding all these volumes, we find volume of required combined solid.

Conversion of Solid from One shape to Another
In this section, we discuss the conversion of solid from one shape to another then, volume of both shapes are always same. For example; there is a bottle of a juice and it was divided into some glasses. Find the number of glasses. So in this case,

where n is number of glasses.

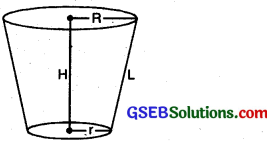
Frustum of a cone:
Frustum of right circular cone
Volume of cone = \(\frac{1}{3}\) π H [R² +r² + Rr]
Curved surface of frustum = πL [R + r]
Total surface area of frustum
= πR² + πr² + πL [R + r].
Slant height of frustum
= \(\sqrt{\mathrm{H}^{2}+(\mathrm{R}-r)^{2}}\)