GSEB Class 10 Maths Notes Chapter 13 પૃષ્ઠફળ અને ઘનફળ

This GSEB Class 10 Maths Notes Chapter 13 પૃષ્ઠફળ અને ઘનફળ covers all the important topics and concepts as mentioned in the chapter.

પૃષ્ઠફળ અને ઘનફળ Class 10 GSEB Notes

→ પ્રાસ્તાવિકઃ ધોરણ 9માં તમે કેટલાક નિયમિત આકારના ઘન પદાર્થો જેવા કે લંબઘન, શંકુ, નળાકાર અને ગોલક તથા અર્ધગોલકથી પરિચિત થયા છો. તમે એ પણ જાણો છો કે આપણે તેમનાં પૃષ્ઠફળ અને ઘનફળ કેવી રીતે શોધી શકીએ. હવે આપણે આ ઘન પદાર્થોનાં સંયોજનથી બનતા ઘન પદાર્થોનો અભ્યાસ કરીશું. વળી, આપણે એક ઘન પદાર્થનું ભિન્ન માપ ધરાવતા તેવા જ ઘન પદાર્થોમાં અથવા અન્ય આકારના ઘન પદાર્થોમાં રૂપાંતરનો પણ અભ્યાસ કરીશું. તદ્ઘપરાંત, શંકુના આડછેદ (Frustum of a cone) તરીકે ઓળખાતા એક ચોક્કસ પ્રકારના ઘન પદાર્થનો પણ અભ્યાસ કરીશું.

→ આ પ્રકરણમાં કુલ પૃષ્ઠફળ (Total Surface Area) માટે TSA પાવપૃષ્ઠોનું પૃષ્ઠફળ (Lateral Surface Area) માટે LSA તથા વક પૃષ્ઠફળ (Curved Surface Area) માટે CSA સંકેતનો ઉપયોગ કરીશું.
કેટલાંક અગત્યનાં સૂત્રોઃ

→ લંબઘન (Cuboid) ધારો કે l, b અને h અનુક્રમે લંબઘનની લંબાઈ, પહોળાઈ અને ઊંચાઈ દર્શાવે છે.

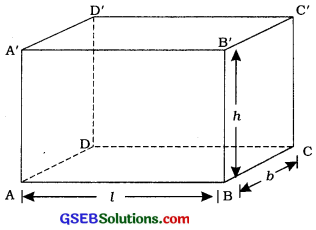
• લંબઘનનું કુલ પૃષ્ઠફળ = 2 (lb + bh + hl)
• લંબઘનના પાર્થપૃષ્ઠોનું પૃષ્ઠફળ = 2h (l + b) = પાયાની પરિમિતિ × ઊંચાઈ
  નોંધઃ ઓરડાની ચાર દીવાલોનું ક્ષેત્રફળ શોધવા લંબઘનના પાર્થપૃષ્ઠોનાં ક્ષેત્રફળના સૂત્રનો ઉપયોગ થાય.
• લંબઘનનું ઘનફળ = lbh
• લંબઘનનો લાંબામાં લાંબો વિકર્ણ = \(\sqrt{l^{2}+b^{2}+h^{2}}\)

→ સમઘન (Cube): ધારો કે, સમઘનની દરેક ધારની લંબાઈ વ છે.

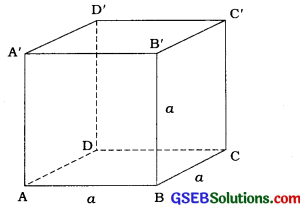
• સમઘનનું TSA = 6a²
• સમઘનનું LSA = 4a²
• સમઘનનું ઘનફળ = a³
• સમઘનનો લાંબામાં લાંબો વિકર્ણ = √3a

→ નળાકાર (Right circular cylinder) ધારો કે, નળાકારની ત્રિજ્યા અને ઊંચાઈ અનુક્રમે r અને છે.

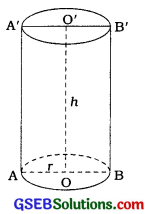
• નળાકારના પાયાનું ક્ષેત્રફળ = πr²
• નળાકારનું CSA
  = 2πrh
  = પાયાનો પરિઘ × ઊંચાઈ
• નળાકારનું TSA = 2πr(n + 1)
• નળાકારનું ઘનફળ = πr²h = પાયાનું ક્ષેત્રફળ × ઊંચાઈ

→ પોલો નળાકાર (Right circular hollow cylinder) ધારો કે, પોલા નળાકારની બહારની (મોટી) ત્રિજ્યા R, અંદરની (નાની) ત્રિજ્યા r અને ઊંચાઈ h છે.

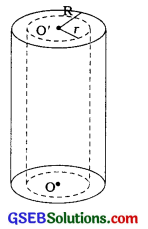
• બે છેડા પૈકી દરેક છેડાનું ક્ષેત્રફળ = π(R² – r²)
• બાહ્ય CSA = 2πRh
• આંતરિક CSA = 2πrh
• કુલ CSA = 2πh(R + r)
• TSA
  = 2πh(R + r) + 2π (R² – r²)
  = 2π(R + r) (h + R- r)
• વપરાયેલ પદાર્થનું ઘનફળ
  = πR²h – πr²h = πh(R² – r²)

→ શંકુ (Right circular cone): ધારો કે, શંકુની ત્રિજ્યા, ઊંચાઈ અને તિર્યક (ત્રાંસી) ઊંચાઈ અનુક્રમે r, h અને l છે.

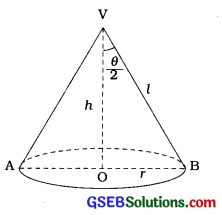
• l² = r² + h²
• CSA = πrl
• TSA = πr (l + r)
• ઘનફળ = \(\frac{1}{2}\) πr²h
  = \(\frac{1}{2}\) × પાયાનું ક્ષેત્રફળ × ઊંચાઈ

→ શંકુનો શિરોકોણ (Vertical angle of a cone) : જ્યારે શંકુના શિરોબિંદુમાંથી પસાર થતું અને પાયાના સમતલને લંબ હોય તેવા સમતલ દ્વારા શંકુના બે ભાગ કરવામાં આવે, તો સમદ્વિભુજ ત્રિકોણ VAB મળે (જુઓ આકૃતિ). Δ VABના ∠AVBને શંકુનો શિરોકોણ કહે છે અને સામાન્ય રીતે તેને θ દ્વારા દર્શાવાય છે. આથી અર્ધશિરોકોણ \(\frac{θ}{2}\)ના ત્રિકોણમિતીય ગુણોત્તર દ્વારા આપણે શંકુના ત્રણ માપ r, h અને l પૈકી એક માપ જાણતા હોઈએ તો બાકીના માપ સહેલાઈથી શોધી શકીએ, કારણ કે sin \(\frac{\theta}{2}=\frac{r}{l}\), cos \(\frac{\theta}{2}=\frac{h}{l}\) અને tan \(\frac{\theta}{2}=\frac{r}{h}\)

→ એક ગોલક (ગોળો – sphere) : ધારો કે, ગોલકની ત્રિજ્યા છે.

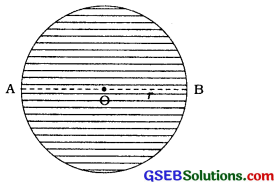
• સપાટીનું ક્ષેત્રફળ = 4πr²
• ઘનફળ = \(\frac{4}{3}\)πr³

→ અર્ધગોલક (અર્ધગોળો – Hemisphere) : ધારો કે અર્ધગોલકની ત્રિજ્યા છે.

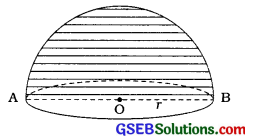
• CSA = 2πr²
• TSA = 3πr²
• ઘનફળ = \(\frac{2}{3}\)πr³ એક

→ પોલો ગોળો (spherical shell): ધારો કે, પોલા ગોળાની બહારની અને અંદરની ત્રિજ્યા અનુક્રમે R અને r છે.

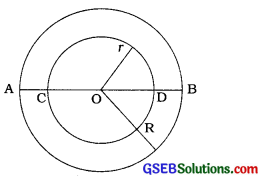
• બાહ્ય સપાટીનું ક્ષેત્રફળ = 4πR²
• આંતરિક સપાટીનું ક્ષેત્રફળ = 4πr²
• વપરાયેલ પદાર્થનું ઘનફળ = \(\frac{4}{3}\)π(R³ – r³)

→ સંયોજિત ઘન પદાર્થોનું કુલ પૃષ્ઠફળ (Surface area of a combination of solids): હવે આપણે ખે અથવા બેથી અધિક મૂળભૂત ઘન પદાર્થો જેવા કે સમઘન, લંબઘન, નળાકાર, શંકુ, ગોલક તથા અર્ધગોલક વગેરેના સંયોજન દ્વારા બનતા પદાર્થોની કુલ સપાટીનું ક્ષેત્રફળ શોધીશું.

→ જ્યારે પણ સંયોજિત ઘન પદાર્થોનું કુલ પૃષ્ઠફળ શોધવાનું થાય, ત્યારે તે સંયોજિત પદાર્થ કયા મૂળભૂત પદાર્થોમાંથી મેળવેલ છે તેનું વિશ્લેષણ કરવું આવશ્યક છે. તે માટે, નિર્દેશ આકૃતિ દોરવી ખૂબ જ મદદરૂપ થઈ પડે છે. વળી, સંયોજિત પદાર્થમાં મૂળ પદાર્થોની અમુક સપાટીઓ ઢંકાઈ જતી હોય, તો તેનું ખાસ ધ્યાન રાખવું જોઈએ.

નોંધઃ સમગ્ર પ્રકરણમાં, જો ની કિંમતનો ઉલ્લેખ ન કર્યો હોય, તો આપણે π = \(\frac{22}{7}\) લઈશું.

→ સંયોજિત ઘન પદાર્થોનું ઘનફળ: પ્રકરણની શરૂઆતમાં આપણે બે જાણીતા ઘન પદાર્થોના સંયોજનથી બનતા ઘન પદાર્થોનું પૃષ્ઠફળ કેવી રીતે મેળવવું તે જોઈ ગયા. અહીં આપણે આવા ઘન પદાર્થોનું ઘનફળ શોધતા શીખીશું. આપણે જોઈશું કે પૃષ્ઠફળની ગણતરીમાં આપણે બે ઘટક પદાર્થોના પૃષ્ઠફળને ઉમેરી શકતા નથી, કારણ કે તેમનો કેટલોક ભાગ બે ઘન પદાર્થોને જોડવાથી દૂર થાય છે. પરંતુ ઘનફળ શોધવામાં સામાન્યતઃ આવું નહિ થાય. બે મૂળભૂત ઘન પદાર્થોને જોડવાથી મળતા ઘન પદાર્થનું ઘનફળ એ સામાન્યતઃ આપેલા બંને ઘન પદાર્થોના ઘનફળના સરવાળા બરાબર થશે. આપણે અહીં “સામાન્યતઃ” શબ્દનો પ્રયોગ ખાસ એટલા માટે કરીએ છીએ કે જો આપેલ પરિસ્થિતિ એવી હોય કે જેમાં એક મૂળભૂત ઘન આકારમાંથી બીજો મૂળભૂત ઘન આકાર કોતરીને દૂર કરવામાં આવેલ હોય, તો આ પરિસ્થિતિમાં મળતા ઘન પદાર્થનું ઘનફળ બંને ઘન પદાર્થોના ઘનફળના તફાવત બરાબર થશે.

→ એક ઘનાકારનું બીજા ઘનાકારમાં રૂપાંતરઃ આપણા રોજિંદા જીવનમાં આપણે એક ઘનાકાર પાત્રમાં રહેલું પ્રવાહી બીજા આકાર કે કદ ધરાવતા ઘનાકાર પાત્રમાં રેડીએ છીએ. વળી, કોઈ ચોક્કસ ઘનાકાર ધરાવતી ધાતુને ઓગાળીને તેને બીજા કોઈ ઘનાકારમાં અથવા તેવા જ પરંતુ જુદા માપ ધરાવતાં ઘનાકારમાં રૂપાંતરિત કરીએ છીએ. આવા રૂપાંતરણ દરમિયાન પ્રવાહી, ધાતુ અથવા બીજા કોઈ પણ પદાર્થનું કદ (ઘનફળ) ફેરવાતું નથી. આપણે ધારી લઈએ છીએ કે રૂપાંતરણ દરમિયાન પદાર્થના કદમાં થતો ઘટાડો ખૂબ જ ઓછી માત્રામાં એટલે કે નગણ્ય હોય છે. જો આવા ઘટાડાની માત્રા વધુ હોય, તો તેનો ઉલ્લેખ આપેલ પ્રશ્નમાં કરવામાં આવે છે.

→ નદી, નહેર અથવા પાઇપમાં પાણીના પ્રવાહનો વેગ અથવા ઝડપ : નળાકાર પાઇપ અથવા લંબઘનાકાર નદી અથવા નહેરમાં વહેતા પાણીની ઝડપ એ અકમ સમયમાં આપેલ બિંદુ આગળથી પસાર થતા પાણીના સ્તંભની ઊંચાઈ દર્શાવે છે.

જો 7 સેમી ત્રિજ્યાવાળી નળાકાર પાઇપમાં વહેતા પાણીની ઝડપ 5 મી સે હોય, તો તે પાઈપ દ્વારા એક સેકન્ડમાં ઠલવાતા પાણીનું ઘનફળ πr²h દ્વારા મળે, જ્યાં n = પાઈપની ત્રિજ્યા = 7 સેમી અને h = પાણીના સ્તંભની ઊંચાઈ = પાણીના પ્રવાહની ઝડપ = 5 મી = 500 સેમી. આમ, એક સેકન્ડમાં પાઇપ દ્વારા ઠલવાતા પાણીનું ઘનફળ
= πr²h
= \(\frac{22}{7}\) × 7 × 7 × 500
= 77000 સેમી
= 77 લિટર

→ પ્રવાહીના ઘનફળના એકમો વચ્ચેના સંબંધઃ

• 1 લિટર = 1000 સેમી³
• 1 મી = 1000000 સેમી = 10⁶ સેમી³
• 1 મી³ = 1000 લિટર
• 1 લિટર = 1000 મિલિ
• 1 સેમી³ = 1 મિલિ

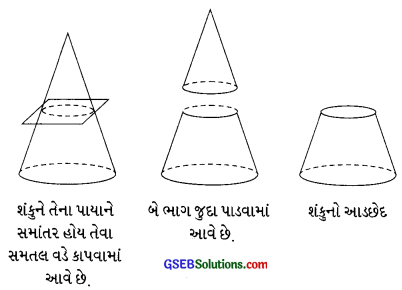
→ શંકુનો આડછેદ (Frustum of a cone) જો કોઈ શંકુ આપેલો હોય અને તેને પાયાને સમાંતર હોય તેવા સમતલ વડે કાપીએ તથા સમતલની એક બાજુ બનતા શંકુને દૂર કરીએ તો સમતલની બીજી બાજુએ શંકુનો આડછેદ કહેવાતો ભાગ બચે છે. શંકુના આડછેદના બે છેડા ભિન્ન ત્રિજ્યાઓવાળા બે વર્તુળ હોય છે.

→ શંકુના આડછેદનાં સૂત્રોઃ

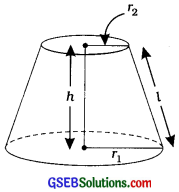
ધારો કે, શંકુના આડછેદની ઊંચાઈ h, તિર્યક ઊંચાઈ l અને ત્રિજ્યા r₁ તથા r₂ (r₁ > r₂) છે, તો શંકુના આડછેદનું ઘનફળ, તેની વક્રસપાટીનું ક્ષેત્રફળ તથા તેની કુલ સપાટીનું ક્ષેત્રફળ નીચેનાં સૂત્રો દ્વારા મળે :
(1) શંકુના આડછેદનું ઘનફળ

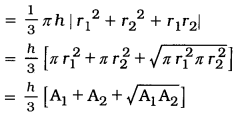
જ્યાં, A₁ અને A₂ એ શંકુના આડછેદના બે છેડાના વર્તુળોના ક્ષેત્રફળ છે.

(2) શંકુના આડછેદની વક્રસપાટીનું ક્ષેત્રફળ
= πl(r₁ + r₂)
= \(\frac{1}{2}\)(2πr₁ + 2πr₂)
= \(\frac{1}{2}\)(C₁ + C₂)
જ્યાં, C₁ અને C₂ એ શંકુના આડછેદના બે છેડાના વર્તુળોના પરિઘ છે અને l = \(\sqrt{h^{2}+\left(r_{1}-r_{2}\right)^{2}}\)

(3) શંકુના આડછેદની કુલ સપાટીનું ક્ષેત્રફળ
= πl(r₁ + r₂) + r₁² + r₂²
જ્યાં, l = \(\sqrt{h^{2}+\left(r_{1}-r_{2}\right)^{2}}\)

→ બે જાણીતા પદાર્થો જેવા કે લંબઘન, શંકુ, નળાકાર, ગોલક અને અર્ધગોલકના સંયોજનથી બનતા પદાર્થનું પૃષ્ઠફળ શોધવું.

→ કોઈ પણ બે પદાથર્યો જેવા કે લંબઘન, શંકુ, નળાકાર, ગોલક અને અર્ધગોલકના સંયોજનથી બનતા પદાર્થનું ઘનફળ શોધવું.

→ જ એક ઘન પદાર્થનું ભિન્ન માપ ધરાવતા તેવા જ ઘન પદાર્થોમાં અથવા અન્ય આકારના ઘન પદાર્થોમાં રૂપાંતર સંબંધી પ્રશ્નોના ઉકેલ શોધવા.

→ આપેલા શંકુના પાયાને સમાંતર સમતલ દ્વારા કાપીએ તથા સમતલની એક બાજુના શંકુને દૂર કરવાથી મળતા ઘનાકારને શંકુનો આડછેદ કહે છે.

→ શંકુના આડછેદસંબંધી સૂત્રો નીચે પ્રમાણે છે:

• શંકુના આડછેદનું ઘનફળ = \(\frac{1}{3}\)πh(r₁² + r₂² + r₁r₂)
• શંકુના આડછેદની વક્રસપાટીનું ક્ષેત્રફળ = πl(r₁ + r₂) જ્યાં, l = \(\sqrt{h^{2}+\left(r_{1}-r_{2}\right)^{2}}\)
• શંકુના આડછેદની કુલ સપાટીનું ક્ષેત્રફળ
  = πl (r₁ + r₂) + π(r₁² + r₂²)

ઉપરનાં સૂત્રોમાં,
h = આડછેદની ઊંચાઈ
l = આડછેદની તિર્ધક ઊંચાઈ
r₁ અને r₂ = શંકુના આડછેદના બંને છેડાની ત્રિજ્યાઓ