GSEB Class 10 Maths Notes Chapter 3 દ્વિચલ સુરેખ સમીકરણયુગ્મ

This GSEB Class 10 Maths Notes Chapter 3 દ્વિચલ સુરેખ સમીકરણયુગ્મ covers all the important topics and concepts as mentioned in the chapter.

દ્વિચલ સુરેખ સમીકરણયુગ્મ Class 10 GSEB Notes

→ તમે દ્વિચલ સુરેખ સમીકરણ અને તેના ઉકેલ વિશે અભ્યાસ કરેલ છે.

→ દ્વિચલ સુરેખ સમીકરણયુગ્મઃ જો a, b અને c એ વાસ્તવિક સંખ્યાઓ હોય અને વ અને b એકસાથે શૂન્ય ન હોય ત્યારે જે સમીકરણને ax + by + c = 0 સ્વરૂપમાં મૂકી શકાય તેને ચલ ૪ અને ચલ પુમાં દ્વિચલ સુરેખ સમીકરણ કહે છે એમ તમે જાણો છો. (a અને b એકસાથે શૂન્ય ન હોઈ શકે
તે શરતને સામાન્ય રીતે a² + b² ≠ 0 વડે પણ દર્શાવાય છે.)

→ ભૌમિતિક રીતે જોતાં, દ્વિચલ સુરેખ સમીકરણનો આલેખ રેખા છે.

→ ax + by + c = 0નો પ્રત્યેક ઉકેલ (x, y)એ સમીકરણને દર્શાવતી રેખા પરના કોઈ બિંદુને સંગત છે અને આનું પ્રતીપ પણ સત્ય છે.

→ જ્યારે માત્ર બે જ ચલ x અને પુનાં બે સુરેખ સમીકરણો એક સાથે લેવામાં આવે ત્યારે તે જોડને દ્વિચલ સુરેખ સમીકરણયુગ્મ કહે છે.

→ ચલ x અને પુમાં દ્વિચલ સુરેખ સમીકરણયુગ્મનું વ્યાપક સ્વરૂપ ax₁ + b₁y + c = 0 અને a₂x + b₂y + c = 0 છે. અહીં a₁, b₁, c₁, a₂, b₂, c₃, બધી વાસ્તવિક સંખ્યાઓ છે અને a₁

a₁² + b₁² = 0, a₂² + b₂² = 0.
દા. ત., 2x + 3y – 13 = 0 અને 3x + 2y – 12 = 0
x – 3y = 0 અને 5x – 3y = 24
x + y = 12 અને 5y = 15.

→ બે ચલ ધરાવતા સુરેખ સમીકરણનો આલેખ દોરવાનો અભ્યાસ ધોરણ IXમાં તમે કરી ચૂક્યા છો. હવે, આપણે બે ચલ ધરાવતા બે સુરેખ સમીકરણોના આલેખ એક જ આલેખપત્ર પર દોરીશું. આ આલેખપત્રમાં, એટલે કે, સમતલમાં ઘેરેલ બે રેખાઓ માટે નીચેની ત્રણ શક્યતાઓમાંથી માત્ર એક હોઈ શકે

• બે રેખાઓ એક બિંદુમાં છેદશે. આ સ્થિતિમાં સમીકરણોની જોડને એક અનન્ય ઉકેલ છે જે તે રેખાઓનાં છેદબિંદુ દ્વારા મળે છે. સમીકરણોની આવી જોડને સુસંગત સમીકરણયુગ્મ કહે છે.
• બે રેખાઓ છેદે નહીં, એટલે કે તેઓ પરસ્પર સમાંતર હોય. આ સ્થિતિમાં સમીકરણોને કોઈ ઉકેલ નથી. આ સંજોગોમાં સમીકરણયુગ્મ અસંગત છે (અથવા તો સુસંગત નથી) તેમ કહેવાય.
• બે રેખાઓ સંપાતી છે, એટલે કે બંને સમીકરણો એક જ રેખા દ્વારા દર્શાવાય છે. આ સ્થિતિમાં સમીકરણયુગ્મને અનંત ઉકેલ છે. આવા સમીકરણયુગ્મને અવલંબી સમીકરણો છે તેમ કહેવાય. સ્પષ્ટ છે કે જે સમીકરણયુગ્મનાં સમીકરણો અવલંબી હોય તે સમીકરણો સુસંગત હોય છે જ.

→ એક દ્વિચલ સુરેખ સમીકરણયુમની રચનાઃ આપણા રોજિંદા જીવનમાં આપણે ઘણી વખત એવા કૂટપ્રશ્નો ઉકેલવાની જરૂર પડે છે કે જે સુરેખ સમીકરણયુગ્મ દ્વારા ઉકેલી શકાય. સામાન્ય રીતે આવા ફૂટપ્રશ્નો બે સંખ્યાઓ, બે અંકની સંખ્યા, કોઈ અપૂર્ણાંક, બે વ્યક્તિઓની ઉંમર, ખૂણાઓ, ઝડપ, લંબાઈ, ટકાવારી વગેરે સંબંધિત હોઈ શકે. આવા કૂટપ્રશ્નોમાં આપેલ બે શરતો પરથી આપણે સુરેખ સમીકરણયુગ્મ રચી શકીએ. તે માટે, જે બે રાશિ આપણે શોધવાની હોય તેમને સામાન્ય રીતે x અને y તરીકે ધારી લેવામાં આવે છે અને ત્યારબાદ પ્રશ્નમાં આપેલ શરતો મુજબ બે સુરેખ સમીકરણો બનાવવામાં આવે છે. ત્યારબાદ એક ભૌમિતિક રીત અને ત્રણ બેજિક રીત પૈકી કોઈ પણ રીતનો ઉપયોગ કરીને આપણે અજ્ઞાત રાશિઓ શોધી શકીએ.

→ દ્વિચલ સુરેખ સમીકરણયુગ્મના ઉકેલની ચકાસણી જવાબમાં મેળવેલ ચલની કિંમતો સમીકરણોમાં મૂકીને સહેલાઈથી થઈ શકે છે. પરંતુ કૂટપ્રશ્ન માટે જ્યારે પણ ચકાસણી કરવી હોય ત્યારે મૂળ પ્રશ્નમાં આપેલ શરતોને આધિન ચકાસણી કરવી જોઈએ, આપણે બનાવેલ સમીકરણો દ્વારા નહીં. યાદ રાખો કે, ચકાસણી કરવી એ પ્રશ્નના ઉકેલનો હિસ્સો નથી, એટલે કે ઉકેલમાં ચકાસણી આવશ્યક નથી.

→ દ્વિચલ સુરેખ સમીકરણયુગ્મના ઉકેલ માટે આલેખની રીતઃ & આલેખાત્મક રજૂઆત : ધોરણ IX માં આપણે ભણી ગયા તે મુજબ કોઈ પણ દ્વિચલ સુરેખ સમીકરણનો આલેખ દોરવા આપણને તેનાં ઓછામાં ઓછા બે ઉકેલની જરૂર પડે. તે ઉકેલો શોધવા માટે આપણે સમીકરણને પુ-સ્વરૂપમાં ફેરવીએ અને ત્યારબાદ ની કોઈ પણ બે અનુકૂળ કિંમતો લઈ પુની કિંમત સરળતાથી શોધી શકાય. ત્યારબાદ ક્રમયુક્ત જોડ (x, U)ને સંગત બિંદુઓ આલેખી તે બિંદુઓમાંથી પસાર થતી રેખા દોરીએ છીએ. આ પ્રમાણે મળેલ રેખા એ આપેલ સમીકરણનો આલેખ અથવા આલેખાત્મક રજૂઆત બને.

→ સુરેખ સમીકરણયુગ્મના પ્રકારઃ

• સુસંગત સમીકરણયુગ્મઃ જે સુરેખ સમીકરણયુગ્મને અનન્ય ઉકેલ હોય અથવા અનંત ઉકેલ હોય તેવા સમીકરણયુગ્મને સુસંગત જોડ કહે છે. જો સમીકરણયુગ્મને અનન્ય ઉકેલ હોય, તો તેમનો આલેખ બે ભિન્ન છેદતી રેખાઓ હોય અને જો સમીકરણયુગ્મને અનંત ઉકેલ હોય, તો તેમનો આલેખ સંપાતી રેખાઓ હોય. સંપાતી રેખાઓ દ્વારા દર્શાવાતા સમીકરણોને અવલંબી સમીકરણો કહે છે.
• અસંગત સમીકરણયુગ્મ: જે સુરેખ સમીકરણયુગ્મને એક પણ ઉકેલ ન હોય તેવા સમીકરણયુગ્મને અસંગત જોડ (સુસંગત ન હોય તેવી જોડ) કહે છે. અસંગત સમીકરણયુગ્મનો આલેખ પરસ્પર સમાંતર રેખાઓ હોય છે.
• અવલંબી સમીકરણયુગ્મ અવલંબી સુરેખ સમીકરણયુગ્મને અનંત ભિન્ન ઉકેલ હોય છે. આવી જોડને અવલંબી સમીકરણયુગ્મ કહે છે. યાદ રાખો કે અવલંબી સમીકરણયુગ્મ હંમેશાં સુસંગત હોય છે. અવલંબી સમીકરણયુગ્મનો આલેખ – સંપાતી રેખાઓ હોય છે.

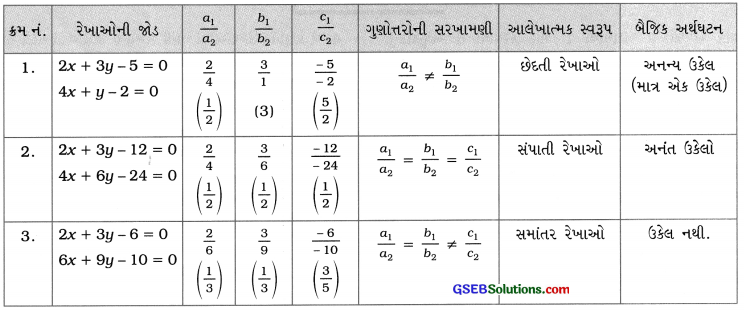
→ સમીકરણયુગ્મનાં સહગુણકો અને તેમનાં પ્રકાર વચ્ચેનો સંબંધ :
ધારો કે, ચલ x અને ઇ ધરાવતાં સમીકરણયુગ્મ a₁x + b₁y + c₁ = 0 અને a₂x + b₂y + c₂ = 0 છે. જ્યાં, a₁² + b₁² ≠ 0 અને a₂² + b₂² ≠ 0.

• જો \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\) તો સમીકરણોની જોડ સુસંગત છે અને તેઓનો આલેખ બે છેદતી રેખાઓ છે.
• જો \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\) તો સમીકરણોની જોડ અસંગત છે અને તેઓનો આલેખ બે સમાંતર રેખાઓ છે.
• જો \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\) તો સમીકરણોની જોડ સુસંગત અને અવલંબી છે તથા તેઓનો આલેખ બે સંપાતી રેખાઓ છે. ઉપર જણાવેલ ત્રણેય શરતોના પ્રતીપ પણ સાચાં છે.

→ ઉપરોક્ત ચર્ચાને આપણે નીચેના કોષ્ટકમાં રજૂ કરી શકીએ :

→ સુરેખ સમીકરણયુગ્મનો ઉકેલ મેળવવાની બૈજિક રીતઃ
સુરેખ સમીકરણયુગ્મનો ઉકેલ મેળવવા માટે ત્રણ બેજિક રીતો છે, જે નીચે મુજબ ઓળખાય છે ?

• આદેશની રીત
• લોપની રીત
• ચોકડી ગુણાકારની રીત

→ આદેશની રીતઃ
સોપાન 1:
અનુકૂળ હોય તે રીતે કોઈ પણ એક સમીકરણમાંથી એક ચલ, ઉદાહરણ તરીકે, અને બીજા ચલ ના સ્વરૂપમાં મેળવો.

સોપાન 2:

• આ સિવાયના સમીકરણમાં પુની કિંમત મૂકતાં, સમીકરણ એક ચલ ના સ્વરૂપમાં મળશે અને આપણે તેને ઉકેલી શકીશું.
• કેટલીક વખત તમે ચલ વિનાનું વિધાન મેળવો તે શક્ય છે. જો આ વિધાન સત્ય હોય, તો તમે અનુમાન કરી શકો કે દ્વિચલ સુરેખ સમીકરણયુગ્મને અનંત ઉકેલો છે. જો આ વિધાન અસત્ય હોય, તો દ્વિચલ સુરેખ સમીકરણયુગ્મ સુસંગત નથી.

સોપાન ૩:
સોપાન 1ની મદદથી બીજા ચલ ની કિંમતને સોપાન 2ના સમીકરણમાં મૂકતાં ચલ ! (અથવા x)ની કિંમત મળશે.

નોંધઃ આપણે એક ચલની કિંમત બીજા ચલના સ્વરૂપમાં મેળવીને સુરેખ સમીકરણયુગ્મનો ઉકેલ મેળવીએ છીએ. તેથી ઉકેલ મેળવવાની આ રીત આદેશની રીત તરીકે ઓળખાય છે.

→ લોપની રીત : દ્વિચલ સુરેખ સમીકરણયુગ્મના ઉકેલ શોધવાની લોપની રીત નીચે મુજબના 4 સોપાનમાં વર્ણવી શકાય:

• સોપાન 1: સૌપ્રથમ બંને સમીકરણોને કોઈ યોગ્ય શૂન્યતર અચળ સંખ્યાઓ વડે ગુણવાથી x અથવા y પૈકી કોઈ એકના સહગુણક) એક ચલના સંહગુણકો સમાન થાય.
• સોપાન 2 ત્યારબાદ એક સમીકરણમાં બીજું સમીકરણ ઉમેરતાં અથવા તેમાંથી બાદ કરતાં એક ચલનો લોપ થશે. જો તમને એક ચલનું સમીકરણ મળે, તો સોપાન 3 પર જાઓ. સોપાન માં આપણને ચલ ન હોય તેવું સત્ય વિધાન મળે, તો સમીકરણયુગ્મને અનંત ઉકેલો મળશે. સોપાન 2માં આપણને ચલ ન હોય તેવું અસત્ય વિધાન મળે, તો સમીકરણયુગ્મને ઉકેલ નથી. એટલે કે તે સુસંગત નથી.
• સોપાન 3: એક ચલ સુરેખ સમીકરણ ઉકેલતાં આપણને (x અથવા y) કોઈ એક ચલની કિંમત મળે.
• સોપાન 4: મૂળ સમીકરણ પૈકીના કોઈ એક સમીકરણમાં x(અથવા પુ)ની કિંમત મૂકતાં આપણને બીજા ચલની કિંમત મળે છે.

→ એક એક વિશિષ્ટ પ્રકારના સુરેખ સમીકરણોઃ જો દ્વિચલ સુરેખ સમીકરણયુગ્મ a₁x + b₁ = c₁ = અને a₂+ b₂y = c₂ માં a₁ = ±b₂ અને a₂ = ±b₁, હોય, તો તેવા સમીકરણોનો સરવાળો અને બાદબાકી લેતાં x + y = d₁ અને x – y = d₂. જેવાં સરળ સમીકરણો મળે અને તે સમીકરણોનો ઉકેલ સહેલાઈથી મેળવી શકાય. ખૂબ મોટા સહગુણકો ધરાવતાં અને ઉપરોક્ત શરતોનું પાલન કરતાં સમીકરણો માટે આ પ્રયુક્તિ ખૂબ જ લાભકારક પુરવાર થાય છે.
દા. ત., 52x+ 48y = 252 અને 48x + 52y = 248નો ઉકેલ શોધો.
52x + 48y = 252 …………(1)
48x + 52y = 248 ………….(2)
સમીકરણ (1) અને (2)નો સરવાળો લેતાં,
100x + 100y = 500 x …………(3)
∴ x + y = 5
સમીકરણ (1) માંથી સમીકરણ (2) બાદ કરતાં,
4x – 4y = 4
∴ x – y = 1 ………(4)
હવે, સમીકરણ 3) અને સમીકરણ (4)નો ઉકેલ x = 3 અને y = 2 સહેલાઈથી મળે.

→ ચોકડી ગુણાકારની રીત : ધારો કે બે ચલ x અને પુનું કોઈ પણ દ્વિચલ સુરેખ સમીકરણયુગ્મ નીચે મુજબ છે:
a₁x+ b₁y + c₁ = 0 ………..(1)
અને a₂x + b₂₁y + c₂ = 0 ……….(2)

ઉપરના સમીકરણોમાંથી x અને પુની કિંમત મેળવવા માટે આપણે નીચે પ્રમાણેનાં સોપાનોને અનુસરીશું:
સોપાન 1:
સમીકરણ (1)ને b₂ વડે અને સમીકરણ (2)ને b₁ વડે ગુણતાં,
b₂a₁x + b₂b₁ + b₂c₁ = 0 ………(3)
b₁a₂x + b₁b₂ + b₁c₂ = 0 ……….(4)

સોપાન 2:
સમીકરણ (3)માંથી સમીકરણ (4) બાદ કરતાં,
(b₂a₁ – b₁a₂) x + (b₂b₂ – b₁b₂)y + (b₂c₁ – b₁c₂) = 0 .
∴ (b₂a₁ – b₁a₂) x = b₁c₂ – b₂c₁
તેથી x = \(\frac{b_{1} c_{2}-b_{2} c_{1}}{a_{1} b_{2}-a_{2} b_{1}}\) જયાં, a₁b₂ – a₂b₁ ≠ 0 ….. (5)

સોપાન 3:
સમીકરણ (1) અથવા (2)માં ની કિંમત મૂકતાં,
આપણને y = \(\frac{c_{1} a_{2}-c_{2} a_{1}}{a_{1} b_{2}-a_{2} b_{1}}\) મળશે ………..(6)
હવે, આપણને બે વિકલ્પો મળશે.
વિકલ્પ 1: a₁b₂ – a₂b₁ ≠ 0.
આ પરિસ્થિતિમાં \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\)
તેથી દ્વિચલ સુરેખ સમીકરણયુગ્મને અનન્ય ઉકેલ મળે.

વિકલ્પ 2: જો a₁b₂ – a₂b₁ = 0, તો આપણે \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}\) k લખીએ, તો a₁ = ka₂, b₁ = kb₂ઝ થશે. સમીકરણ (1)માં a, અને bjની કિંમતો મૂકતાં, આપણને k (a₂x + b₂y) + c = 0 મળશે. …. (7) સમીકરણ () અને (2) બંને સમીકરણોનું સમાધાન માત્ર c₁ = ₂, એટલે કે \(\frac{c_{1}}{c_{2}}\) = k માટે થાય છે તેમ અવલોકન કરી શકાય.

જો c₁ = kc₂, તો સમીકરણ (2)નો કોઈ પણ ઉકેલ સમીકરણ (1)નું સમાધાન કરશે અને તેથી ઊલટું પણ શક્ય છે.
તેથી જો \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\), તો દ્વિચલ સુરેખ સમીકરણ યુગ્મ (1) અને (2)ને અનંત ઉકેલો છે.

જો c₁ ≠ kc₂, તો સમીકરણ (2) માટેનો કોઈ પણ ઉકેલ સમીકરણ (1)નું સમાધાન નહીં કરે અને તેથી ઊલટું પણ શક્ય છે. તેથી સમીકરણયુગ્મને ઉકેલ નથી. આપણે, દ્વિચલ સુરેખ સમીકરણયુગ્મ (1) અને (2)ની ઉપર્યુક્ત ચર્ચાને સંક્ષિપ્તમાં નીચે પ્રમાણે દર્શાવી શકીએ:

• જ્યારે \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\) ત્યારે આપણને અનન્ય ઉકેલ મળે છે.
• જ્યારે \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\). ત્યારે અનંત ઉકેલો મળે છે
• જ્યારે \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}\) તથા \(\frac{a_{1}}{a_{2}} \neq \frac{c_{1}}{c_{2}}\) અને \(\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\) છે. ત્યારે ઉકેલ નથી.

→ ચોકડી ગુણાકારની રીતનો ઉપયોગ ચોકડી ગુણાકારની રીતથી દ્વિચલ સુરેખ સમીકરણયુગ્મનો ઉકેલ શોધવા આપણે નીચેના સોપાનોને અનુસરીએ છીએ:
સોપાન 1:
આપેલ સમીકરણોને પ્રમાણિત સ્વરૂપમાં દર્શાવોઃ
a₁x + b₁y + c₁ = 0 …… (1)
a₁x + b₁y + c₂ = 0 …. (2)

સોપાન 2:

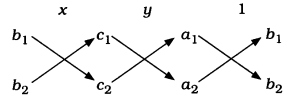
સહગુણકો a₁, a₂, b₁, અને b₂ઝ તથા અચળાંકો c₁ અને c₂ને x, , અને 1ની નીચે ઉપરની આકૃતિમાં બતાવ્યા મુજબ ગોઠવો. ત્યારબાદ ચોકડી દ્વારા દર્શાવેલ સંખ્યાઓના ગુણાકાર કરીને નીચે મુજબનું સમીકરણ લખો:
\(\frac{x}{b_{1} c_{2}-b_{2} c_{1}}=\frac{y}{c_{1} a_{2}-c_{2} a_{1}}=\frac{1}{a_{1} b_{2}-a_{2} b_{1}}\)

સોપાન 3:
જો a₁b₂ – a₂b₁ ≠ 0 હોય, તો સોપાન 2માં મેળવેલ સમીકરણમાંથી x અને પુની કિંમતો શોધો.

નોંધઃ જો નો છેદ એટલે કે b₁c₂ – b₂c₁ = 0 હોય, તો xની કિંમત શૂન્ય થાય અને જો પુનો છેદ એટલે કે c₁a₂ – c₂a₁ = 0 હોય, તો જુની કિંમત શૂન્ય થાય.

→ દ્વિચલ સુરેખ સમીકરણના સ્વરૂપમાં પરિવર્તિત કરી શકાય તેવાં સમીકરણો હવે, આપણે સુરેખ ન હોય, પરંતુ યોગ્ય આદેશ વડે સુરેખ સમીકરણોમાં રૂપાંતરિત કરી શકાય એવાં સમીકરણયુગ્મનો અભ્યાસ કરીશું. જેમ કે, \(\frac{4}{x}+\frac{9}{y}\) = 5 એ સુરેખ સમીકરણ નથી, પરંતુ \(\frac{1}{x}\) = a અને \(\frac{1}{y}\) = b, આદેશ લેવાથી તે 4a + 9b = 5માં પરિવર્તિત થાય છે જે સુરેખ સમીકરણ છે. તે જ રીતે \(\frac{10}{x+y}+\frac{9}{x-y}\) = 5 એ સુરેખ સમીકરણ નથી, પરંતુ \(\frac{1}{x+y}\) = 2 અને \(\frac{1}{x-y}\) = b આદેશ લેવાથી તે 10a + 9b = 5માં પરિવર્તિત થાય છે જે સુરેખ સમીકરણ છે. સમીકરણ \(\frac{14}{2 x+3 y}+\frac{3}{2 x-3 y}\) = 5 પણ સુરેખ સમીકરણ નથી, પરંતુ \(\frac{1}{2 x+3 y}\) = a અને \(\frac{1}{2 x-3 y}\)= b આદેશ લેતાં તેને પણ સુરેખ સમીકરણ 14a + 3b = 5માં પરિવર્તિત કરી શકાય છે.

→ સમીકરણયુગ્મ 7x – 2y = 5xy અને 8x + 7y = 15xy (x ≠ 0, y ≠ 0) એ સુરેખ સમીકરણયુગ્મ નથી, કારણ કે તેમાં દ્વિઘાતવાળું ને સમાવતું પદ આવેલ છે. આવા સમીકરણોનો
ઉકેલ તેમને સુરેખ સમીકરણોમાં પરિવર્તિત કર્યા વગર પણ નીચે દર્શાવ્યા મુજબ મેળવી શકાય
7x – 2y = 5xy …………(1)
8x+ 7y = 15xy. ….(2) સમીકરણ (1)ને 7 વડે અને સમીકરણ (2)ને 2 વડે
49x – 14y = 35xy …….. (3)
16x + 140y = 30xy ….. (4)

સમીકરણો (3) અને (4)નો સરવાળો લેતાં,
(49x – 140y) + (16x + 14y) = 35xy + 30xy
∴ 65x = 65g.
∴ y = 1 (∵ x ≠ 0).
સમીકરણ (1)માં y = 1 મૂક્તાં,
∴ 7x – 2 (1) = 5x (1)
∴ 2x = 2 .
∴ x = 1
આમ, આપેલ સુરેખ ન હોય તેવા સમીકરણયુગ્મનો ઉકેલ x = 1, y = 1 છે.

→ એકના એક જ બે ચલમાં બે સુરેખ સમીકરણોને આપણે દ્વિચલ સુરેખ સમીકરણયુગ્મ કહીશું.

→ દ્વિચલ સુરેખ સમીકરણયુગ્મનું વ્યાપક સ્વરૂપ a₁x+ b₁y + c₁ = 0, a₂x + b₂y + c₂ = 0
જ્યા, a₁, a₂ b₁, b₂, c₁, c₂, વાસ્તવિક સંખ્યાઓ છે. તથા a₁ ²+ b₁² ≠ 0, a₂ ²+ b₂² ≠ 0.

→ દ્વિચલ સુરેખ સમીકરણયુગ્મનો ઉકેલ મેળવવાની બે રીતો છેઃ

• આલેખની રીત
• બૈજિક રીત

→ આલેખની રીત સુરેખ સમીકરણયુગ્મનો આલેખ એક જ આલેખપત્ર પર બે રેખાઓ દર્શાવે છે.

• જો ઉપરોક્ત બંને રેખાઓ પરસ્પર છેદે, તો સમીકરણયુગ્મને અનન્ય ઉકેલ હોય અને બે રેખાઓના અનન્ય છેદબિંદુના યામ એ સમીકરણયુગ્મનો ઉકેલ દર્શાવે. આ પરિસ્થિતિમાં આપેલ સમીકરણયુગ્મ સુસંગત છે તેમ કહેવાય.
• જો બંને રેખાઓ સંપાતી હોય, તો રેખા પરના અનંત બિંદુઓનાં યામ સમીકરણનો ઉકેલ દર્શાવે છે. તેથી સમીકરણયુગ્મને અનંત ઉકેલ છે તેમ કહેવાય. બંને સમીકરણો સુરેખ અવલંબી છે તેમ કહેવાય.
• જો બંને રેખાઓ સમાંતર હોય, તો તેમનું સામાન્ય બિંદુ ન મળે. આ પરિસ્થિતિમાં સમીકરણયુગ્મને કોઈ વાસ્તવિક ઉકેલ નથી. સમીકરણો સુસંગત નથી તેમ કહેવાય.

→ સુરેખ સમીકરણયુગ્મના ઉકેલ માટે ત્રણ બેજિક રીતો છે:

• આદેશની રીત
• લોપની રીત
• ચોકડી ગુણાકારની રીત

→ સુરેખ સમીકરણયુગ્મ a₁x + b₁y + c₁ = 0 અને a₂x + b₂y + c₂ = 0 માટે નીચે આપેલા વિકલ્પો ઉદ્ભવે છેઃ

• \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\) આ સ્થિતિમાં સુરેખ સમીકરણયુગ્મ સુસંગત છે.
• \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} ; \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\) તથા \(\frac{a_{1}}{a_{2}} \neq \frac{c_{1}}{c_{2}}\) આ સ્થિતિમાં સુરેખ સમીકરણયુગ્મ સુસંગત નથી.
• \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\) આ સ્થિતિમાં સુરેખ સમીકરણયુગ્મ સુસંગત છે અને અવલંબી છે.

→ સુરેખ ન હોય તેવાં કેટલાંક સમીકરણોને યોગ્ય આદેશ પસંદ કરી સુરેખ સમીકરણમાં રૂપાંતર કરી શકાય.