GSEB Class 10 Maths Notes Chapter 4 દ્વિઘાત સમીકરણ

This GSEB Class 10 Maths Notes Chapter 4 દ્વિઘાત સમીકરણ covers all the important topics and concepts as mentioned in the chapter.

દ્વિઘાત સમીકરણ Class 10 GSEB Notes

→ પ્રકરણ 2માં ભણ્યા તેમ ax + bx + c, a ≠ 0 એ દ્વિઘાત બહુપદી છે. જો આ દ્વિઘાત બહુપદીનું મૂલ્ય શૂન્ય લેવામાં આવે, તો આપણને દ્વિઘાત સમીકરણ ax² + bx + c = 0, a ≠ 0 મળે. વાસ્તવિક જીવનસંબંધી ઘણા બધા પ્રશ્નોમાં દ્વિઘાત સમીકરણનો ઉપયોગ થાય છે.

→ ઘણા લોકો માને છે કે સૌપ્રથમ બૅબિલોનવાસીઓએ દ્વિઘાત સમીકરણનો ઉકેલ મેળવ્યો. ગ્રીક ગણિતશાસ્ત્રી યુક્લિડે દ્વિઘાત સમીકરણનો ઉકેલ શોધવાની રીત વિકસાવી. સામાન્ય રીતે, દ્વિઘાત સમીકરણ ઉકેલવાનો શ્રેય મોટે ભાગે પ્રાચીન ભારતીય ગણિતશાસ્ત્રીઓને જાય છે. વાસ્તવમાં, બ્રહ્મગુપ્ત (Brahmagupta) (ઈ. સ. 598 – 665) ax² + bx = c દ્વિઘાત સમીકરણના ઉકેલ માટે સ્પષ્ટ સૂત્ર આપ્યું. પછીથી શ્રીધર આચાર્ય (Shridhar Acharya) (ઈ. સ. 1025) દ્વિઘાત સૂત્ર તરીકે ઓળખાતું સૂત્ર પ્રસ્થાપિત કર્યું. (તેનો ઉલ્લેખ ભાસ્કર 1માં કરેલ છે.) તેમાં દ્વિઘાત સમીકરણનો ઉકેલ મેળવવા માટે પૂર્ણવર્ગની રીતનો ઉપયોગ કરાય છે.

→ એક અરબ ગણિતશાસ્ત્રી અલ-બ્લારિઝમીએ (Al-Khwarizmi) (લગભગ ઈ. સ. 800) પણ વિવિધ પ્રકારનાં દ્વિઘાત સમીકરણનો અભ્યાસ કર્યો હતો. અબ્રાહમ બાર હિયા હા-નાસીએ (Abraham bar Hiyya Ha-nast) યુરોપમાં ઈ. સ. 1145માં તેણે લખેલ પુસ્તક Liber Embadorumમાં ભિન્ન ભિન્ન દ્વિઘાત સમીકરણના પૂર્ણ ઉકેલ આપ્યા.

→ દ્વિઘાત સમીકરણઃ a, b, c વાસ્તવિક સંખ્યાઓ છે તથા a ≠ 0 માટે ચલ માં દ્વિઘાત સમીકરણ ax² + bx + c = 0 પ્રકારનું હોય છે.

→ હકીક્તમાં, p (x) = 0 પ્રકારનું કોઈ પણ સમીકરણ, જ્યાં p (x) એ દ્વિઘાત બહુપદી છે, એ દ્વિઘાત સમીકરણ છે. પરંતુ, જ્યારે આપણે p(x)નાં પદોનો ની ઘાતના ઊતરતા ક્રમમાં લખીએ ત્યારે દ્વિઘાત સમીકરણનું પ્રમાણિત સ્વરૂપ મળે છે. આમ, ax² + bx + c = 0, a ≠ 0ને દ્વિઘાત સમીકરણનું પ્રમાણિત સ્વરૂપ કહે છે.

→ આપણી આસપાસની દુનિયામાં અનેક જુદી જુદી સ્થિતિમાં અને ગણિતનાં ભિન્ન ક્ષેત્રોમાં દ્વિઘાત સમીકરણનો ઉદ્ભવ થતો હોય છે. દા. ત., એવી બે ધન સંખ્યાઓ (લંબચોરસની લંબાઈ અને પહોળાઈ) શોધવાની હોય કે જેમનો સરવાળો (લંબચોરસની અર્ધપરિમિતિ) 35 થાય અને ગુણાકાર (લંબચોરસનું ક્ષેત્રફળ) 300 થાય, તો આપણને ax² – 35x + 300 = 0 સમીકરણ મળે.

→ અવયવીકરણ વડે દ્વિઘાત સમીકરણનો ઉકેલ

• જો aα² + bα + c = 0 હોય, તો વાસ્તવિક સંખ્યા α એ દ્વિઘાત સમીકરણ ax² + bx + c = 0, a ≠ 0નું બીજ કહેવાય.
• બીજા શબ્દોમાં, x = α એ દ્વિઘાત સમીકરણનો ઉકેલ છે અથવા a દ્વિઘાત સમીકરણનું સમાધાન કરે છે.
• દ્વિઘાત બહુપદી ax²+ bx + cનાં શૂન્યો તથા દ્વિઘાત સમીકરણ ax² + bx + c = 0નાં બીજ સમાન છે.
• આપણે જાણીએ છીએ કે, દ્વિઘાત બહુપદીને વધુમાં વધુ 2 શૂન્યો હોય. આથી કોઈ પણ દ્વિઘાત સમીકરણને વધુમાં વધુ 2 બીજ હોય. કેટલીક વાર દ્વિઘાત સમીકરણને માત્ર એક જ (સમાન અથવા પુનરાવર્તિત) વાસ્તવિક બીજ હોય છે અને કેટલીક વાર દ્વિઘાત સમીકરણને એક પણ વાસ્તવિક બીજ નથી હોતું.

→ દ્વિઘાત સમીકરણનો અવયવીકરણ દ્વારા ઉકેલઃ જો દ્વિઘાત સમીકરણ ax² + bx + c = 0ને (px + q) (x + 5) = 0, p ≠ 0, r ≠ 0 સ્વરૂપમાં દર્શાવી શકાય, તો દરેક સુરેખ અવયવ px + q અને rx + sને શૂન્ય સાથે સરખાવતાં આપણને દ્વિઘાત સમીકરણ ax² + bx + c = 0 નાં બે બીજ \(-\frac{q}{p}\) અને \(-\frac{s}{r}\) મળે છે.

→ દ્વિઘાત સમીકરણના ઉકેલ અવયવીકરણ દ્વારા મેળવવાની રીતનાં સોપાનઃ

• સમીકરણમાં આવતા કૌંસ અને અપૂર્ણાંકને (જો હોય તો) દૂર કરો.
• સમીકરણનાં બધાં જ પદોને ડાબી બાજુએ લઈને સમીકરણની જમણી બાજુને શૂન્ય (0) બનાવો. જેથી સમીકરણ ax² + bx + c = 0 સ્વરૂપમાં ફેરવાય.
• ડાબી બાજુએ રહેલ પદાવલી ax² + bx + cનાં બે સુરેખ અવયવો px + q અને rx + s મેળવો; જ્યાં p ≠ 0, r ≠ 0
• દરેક સુરેખ અવયવને શૂન્ય સાથે સરખાવીને તેમના ઉકેલ \(-\frac{q}{p}\) તથા \(-\frac{s}{r}\) મેળવો, જે આપેલ દ્વિઘાત સમીકરણના ઉકેલ થાય.

→ દ્વિઘાત સમીકરણ આધારિત ફૂટપ્રશ્નોઃ દ્વિઘાત સમીકરણનો ઉપયોગ કરવો પડે તેવા કૂટપ્રશ્નો(શાબ્દિક પ્રશ્નો)માં અમુક વખત એક જ રાશિ શોધવાની હોય અને અમુક વખત એક કરતાં વધુ રાશિઓ શોધવાની હોય છે. આવા કૂટપ્રશ્નોનો ઉકેલ શોધવા સૌપ્રથમ તો પ્રશ્નોને ચીવટપૂર્વક વાંચો અને શોધવાની હોય તે રાશિ અથવા રાશિઓ નક્કી કરો. ત્યારબાદ તે પૈકી એક રાશિ માટે x (અથવા અન્ય કોઈ પણ અક્ષર) ધારો. બીજી અજ્ઞાત રાશિ xના સ્વરૂપમાં મેળવો. ત્યારબાદ આપેલ શરત અનુસાર દ્વિઘાત સમીકરણ રચો. તે સમીકરણને દ્વિઘાત સમીકરણના પ્રમાણિત સ્વરૂપ ax² + bx + c = 0ના સ્વરૂપમાં ફેરવો. આ સમીકરણનો ઉકેલ મેળવીને ની કિંમત અથવા કિંમતો મેળવો. જો કોઈ કિંમત એવી મળે કે જે અશક્ય હોય, તો તેને જતી કરો. ૮ની મળેલ કિંમત અનુસાર શોધવાની રાશિ અથવા રાશિઓની કિંમત મેળવો.

બે સંખ્યાઓ પર આધારિત, બે અંકની સંખ્યા પર આધારિત, ક્રમિક સંખ્યાઓ પર આધારિત, ઉંમર આધારિત, ઝડપ-અંતરસમય આધારિત, ભૂમિતિ આધારિત એવા ઘણા પ્રકારના કૂટપ્રશ્નો હોય છે. જેને દ્વિઘાત સમીકરણની મદદથી ઉકેલી શકાય છે.

→ પૂર્ણવર્ગની રીતે દ્વિઘાત સમીકરણનો ઉકેલ કોઈ પણ દ્વિઘાત સમીકરણમાં યોગ્ય અચળ ઉમેરીને અથવા બાદ કરીને આપણે તે સમીકરણને (x ± a)² – b² = 0, એટલે કે, (x ± a)² = b² સ્વરૂપમાં સરળતાથી ફેરવી શકીએ. ત્યારબાદ તેના ઉકેલ સહેલાઈથી મળી શકે. આ પ્રવિધિને પૂર્ણવર્ગની રીત કહેવાય છે. જેની સમજૂતી નીચે આપેલ મુજબનાં સોપાનોથી સ્પષ્ટ થાય છે.

→ પૂર્ણવર્ગની પ્રવિધિઃ
(1) આપેલ દ્વિઘાત સમીકરણને પ્રમાણિત સ્વરૂપ ax² + bx + c = 0, a ≠ 0માં લખો.

(2) જો a ≠ 1, તો સમીકરણના દરેક પદને વ વડે ભાગીને સમીકરણ x² + \(\frac{b}{a}\)x + \(\frac{c}{a}\) = 0 મેળવો.

(3) અચળ પદ \(\frac{c}{a}\)ને જ.બા.માં લઈ જઈને નીચેનું સ્વરૂપ મેળવો:
x² + \(\frac{b}{a}\)x = –\(\frac{c}{a}\)

(4) સમીકરણની બંને બાજુ \(\left(\frac{b}{2 a}\right)^{2}\) એટલે કે,

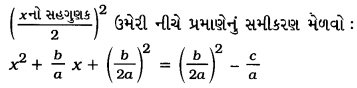
(5) અહીં, ડા.બા. એ x + \(\frac{b}{2a}\) નો વર્ગ છે અને જ.બા.નું – સાદું રૂપ \(\frac{b^{2}-4 a c}{4 a^{2}}\)-વદ થાય. આથી સમીકરણ નીચે મુજબ
\(\left(x+\frac{b}{2 a}\right)^{2}=\frac{b^{2}-4 a c}{4 a^{2}}\)

(6) જો b² – 4ac ≥ 0 હોય, તો બંને બાજુ વર્ગમૂળ લેતાં
\(x+\frac{b}{2 a}=\pm \frac{\sqrt{b^{2}-4 a c}}{2 a}\) મળે.

(7) આ પરથી સમીકરણ ax² + bx + c = 0ના ઉકેલ નીચે મુજબ મળે :
x = \(\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
નોંધઃ જો b² -4ac < 0 હોય, તો સમીકરણના વાસ્તવિક બીજનું અસ્તિત્વ નથી.

→ અપૂર્ણાકનો ઉપયોગ ન આવે તેવી બીજી સરળ રીત:
ax²+ bx + c = 0.
∴ 4a²x² + 4abx + 4ac = 0 (4a ≠ 0 વડે ગુણતા)
∴ 4a²x² + 4abx + b² – b² + 4ac = 0 (b² ઉમેરતાં અને બાદ કરતાં) .
∴ (2ax + b)² – (b² – 4ac) = 0.

→ દ્વિઘાત સૂત્રના ઉપયોગ દ્વારા દ્વિઘાત સમીકરણના ઉકેલ શોધવા ધારો કે, આપેલ દ્વિઘાત સમીકરણ ax² + bx + c = 0 છે. સમીકરણના દરેક પદને a ≠ 0 વડે ભાગતાં,

આમ, દ્વિઘાત સમીકરણ ax² + bx + c = 0ના બીજ x = \(\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\) છે.

નોંધઃ દ્વિઘાત સમીકરણના ઉકેલ શોધવાના આ સૂત્રને દ્વિઘાત સૂત્ર અથવા શ્રીધરાચાર્ય સૂત્ર કહેવાય છે.

→ દ્વિઘાત સૂત્રની રીત એ દ્વિઘાત સમીકરણના ઉકેલ શોધવાની ટૂંકી, સરળ અને સુંદર રીત છે. જેમાં a, b અને c આધારિત થોડી જ ગણતરીઓ કરવાની હોય છે. આથી બીજી કોઈ રીત કરતાં આ રીતને વધુ પસંદ કરવામાં આવે છે.

→ દ્વિઘાત સમીકરણના ઉકેલ માટેની આપણે ત્રણ રીત – અવયવીકરણની રીત, પૂર્ણવર્ગની રીત અને દ્વિઘાત સૂત્રની રીત શીખ્યા. જો પ્રશ્નમાં કોઈ ચોક્કસ રીતનો ઉલ્લેખ કર્યો હોય, તો તે જ રીતને અનુસરવી. પરંતુ, જો પ્રશ્નમાં કોઈ પણ રીતનો ઉલ્લેખ કરેલ ન હોય, તો અનુકૂળ કોઈ પણ રીત પસંદ કરવી.

→ જ પૂર્ણવર્ગની રીત તથા દ્વિઘાત સૂત્રની રીતમાં b² – 4acની કિંમત સમીકરણના ઉકેલોના પ્રકાર નક્કી કરે છે, જેનો અભ્યાસ આપણે આ પ્રકરણમાં આગળના વિભાગમાં કરીશું.

→ અમુક વાર 4 ઘાત ધરાવતા y⁴ – 25y2 + 144 = 0 જેવા સમીકરણને y² = x આદેશ લેવાથી દ્વિઘાત સમીકરણ x² – 25x + 144 = 0 સ્વરૂપમાં ફેરવી શકાય છે.

→ આ જ રીતે \(\frac{x}{x+1}+\frac{x+1}{x}=\frac{61}{30}\) સ્વરૂપના સમીકરણને \(\frac{x}{x+1}\) = આદેશ લેતાં, m + \(\frac{1}{m}\) = એટલે કે, 30m² – 6lm + 30 = 0 સ્વરૂપમાં ફેરવીને સહેલાઈથી ઉકેલી

→ બીજનાં સ્વરૂપ: દ્વિઘાત સમીકરણ ax² + bx + c = 0 માટે, b² – 4acની કિંમતને વિવેચક કહેવામાં આવે છે. b² – 4acની કિંમત (જને સંકેત D દ્વારા પણ અમુક વાર દર્શાવાય છે.) એ આપેલ સમીકરણનાં બીજ વાસ્તવિક છે કે નહીં તે નક્કી કરે છે.

વિવેચકની કિંમત	બીજનો પ્રકાર
ધન	વાસ્તવિક અને ભિન્ન
શૂન્ય	વાસ્તવિક અને સમાન
ઋણ	વાસ્તવિક બીજ ન મળે

નોંધઃ

• જો વ, b અને તે સંમેય સંખ્યાઓ હોય તથા b² – 4acની કિંમત ધન અને પૂર્ણવર્ગ હોય, તો સમીકરણનાં બીજ સંમેય અને ભિન્ન મળે.
• જો a, b અને તે સંમેય સંખ્યાઓ હોય તથા b² – 4acની કિંમત ધન હોય પરંતુ પૂર્ણવર્ગ ન હોય, તો સમીકરણનાં બીજ અસંમેય અને ભિન્ન મળે.
• જો b² – 4ac = 0 હોય, તો સમીકરણનાં બીજ સમાન મળે અને દરેક બીજની કિંમત – થાય.

→ અસમતાના કેટલાક ગુણધર્મો

• ax – b > 0 પરથી, જો a > 0 હોય, તો x > \(\frac{b}{a}\) અને જો a < 0 હોય, તો x < \(\frac{b}{a}\) મળે. (અસમતાને ત્રણ સંખ્યા વડે ગુણવાથી અસમતા ફેરવાય છે.)
• x² – a² ≥ 0 હોય, તો x ≤ – a અથવા x ≥ a.
• x² – a² > 0 હોય, તો x < -a અથવા x ≥ a.
• x² – a² < 0 હોય, તો – a < x< a.
• (x – a) (x – b) > 0 અને a < b હોય, તો x < a અથવા x > b.
• (x – a) (x – b) < 0 અને a < હોય, તો a < x < b.

→ ચલ માં દ્વિઘાત સમીકરણ a, b, c વાસ્તવિક સંખ્યાઓ અને a ≠ 0 માટે ax² + bx + c = 0 પ્રકારનું હોય.

→ જો ax² + bx + c = 0 હોય, તો વાસ્તવિક સંખ્યા a દ્વિઘાત સમીકરણ ax² + bx + c = 0નું એક બીજ કહેવાય. દ્વિઘાત બહુપદી ax² + bx + cનાં શૂન્યો અને દ્વિઘાત સમીકરણ ax² + bx + c = 0નાં બીજ સમાન હોય. જો આપણે ax² + bx + c = 0 અને સુરેખ અવયવના ગુણાકાર સ્વરૂપે દર્શાવી શકીએ,

→ દ્વિઘાત સમીકરણ ax² + bx + c = 0નાં બીજ દરેક અવયવનું મૂલ્ય શૂન્ય લઈ મેળવી શકીએ. પૂર્ણવર્ગ બનાવવાની રીતનો ઉપયોગ કરીને પણ દ્વિઘાત સમીકરણનો ઉકેલ મેળવી શકાય.

→ દ્વિઘાત સૂત્ર :દ્વિઘાત સમીકરણ ax² + bx + c = 0નાં બીજ \(\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)તરીકે મળે, જ્યાં b² -4ac ≥ 0.

→ કવિાત સમીકરણ ax² + bx + c = 0માં

• જો b² – 4ac > 0 તો, બે ભિન્ન વાસ્તવિક બીજ મળે.
• જો b² – 4ac = 0 તો, બે સમાન બીજ મળે.
• જો b² – 4ac < 0 તો, વાસ્તવિક બીજ ના મળે.

→ જો α અને β એ દ્વિઘાત સમીકરણ ax² + bx + c = 0નાં
બીજ હોય, તો α + β = \(\frac{-b}{a}\) અને αβ = \(\frac{c}{a}\)

→ α અને β બીજ ધરાવતું દ્વિઘાત સમીકરણ x² – (α + β)x + αβ = 0 દ્વારા મળે.

→ જો દ્વિઘાત સમીકરણ ax² + bx + c = 0નાં બીજ વિરોધી સંખ્યાઓ હોય, તો b = 0 અને જો તેના બીજ વ્યસ્ત સંખ્યાઓ હોય, તો a = c.