GSEB Class 10 Maths Notes Chapter 5 Arithmetic Progressions

This GSEB Class 10 Maths Notes Chapter 5 Arithmetic Progressions covers all the important topics and concepts as mentioned in the chapter.

Arithmetic Progressions Class 10 GSEB Notes

You must have observed that in nature, many things follow a certain pattern, such as the petals of a sunflower, the holes of a honeycomb, the grains on a maize cob, the spirals on a pineapple and on a pine cone etc.

In this chapter, we shall discuss patterns in which succeeding terms are obtained by adding a fixed number to the preceding terms. We shall also see how to find their nth terms and the sum of n consecutive terms, and use this knowledge in solving some daily life problems.

Arithmetic Progression
An arithmetic progression is a list of numbers in which each term is obtained by adding a fixed number to the preceding term except the first term.

This fixed number is called the common difference of the A.P. Remember that it can be positive, negative or zero.
Let us denote the first term of an A.P. by av second term by a₂,…., nth term by an and the common difference by d. Then the A.P. becomes a₁, a₂, a₃, …………, a_n.

So, a₂ – a₁ = a₃ – a₂ = … = a_n – a_n-1 = d.
a, a + d, a + 2d, a + 3d,… represents an arithmetic progression where a is first term and d the common difference. This is called the general form of an A.P.

nth term of an A.P.
Let a₁, a₂, a₃,…. be an AP whose first term aj is a and the common difference is d.
Then, the second term a₂ = a + d
= a + (2 – 1)d
the third term a₂ = a₂ + d
= (a + d) + d = a + 2d = a + (3 – 1)d
the fourth term a₄ = a₃ + d
= (a + 2d) + d = a + 3d
= a + (4 – 1)d
……………….
……………….

Looking at the pattern, we can say that die nth term an = a + (n – 1) d
So, the nth term an of the AP with first term a and common difference d is given by an = a + (n – 1)d
an or In is also called the general term of the AP. If there are m terms in the AP, then am represents the last term which is sometimes also denoted by l.

Sum of first n Terms of an AP
Let n terms of an A.P. are a, a + d, a + 2d…., a + (n – 1) d
The nth term of this AP is a + (n – 1)d. Let S denote the sum of the first n terms of the A.P. We have,
S = a + (a + d) + (a + 2d) + ……..+ [a + (n – 1) d] ………… (1)

Rewriting the terms in reverse order, we have
S = [a + (n – 1) d] + [a + n – 2) d] +…+ (a + d) + a ………….(2)

On adding (1) and (2) above, we get

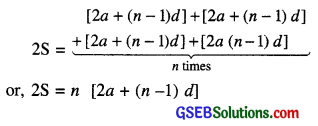
(Since there are n terms)
or, S = \(\frac{n}{2}\) [2a + (n – 1) d]
So, the sum of the first n terms of an AP is given by
S = \(\frac{n}{2}\) [2a + (n – 1) d]

We can also write this as n
S = \(\frac{n}{2}\) [a + a + (n – 1) d]
i. e., S = \(\frac{n}{2}\) (a + a_n) ………..(3)

Now, if there are only n terms in an AP, then an = l, the last term.
From (3), we see that
S = \(\frac{n}{2}\)(a + l) ……..(4)
This form of the result is useful when the first and the last terms of an AP are given and the common difference is not given.