This GSEB Class 10 Maths Notes Chapter 6 ત્રિકોણ covers all the important topics and concepts as mentioned in the chapter.
ત્રિકોણ Class 10 GSEB Notes
→ પ્રાસ્તાવિકઃ જ સમરૂપતાનો પરિચય તમે અગાઉના ધોરણમાં કરેલ અભ્યાસ પરથી ત્રિકોણ અને તેના ઘણા ગુણધર્મોથી પરિચિત થયા છો. ધોરણ IXમાં તમે ત્રિકોણની એકરૂપતા વિશે વિગતવાર અભ્યાસ કર્યો છે. યાદ કરો કે, જ્યારે બે આકૃતિઓના આકાર અને કદ સમાન હોય ત્યારે તે બે આકૃતિઓ એકરૂપ છે તેવું કહેવાય. આ પ્રકરણમાં આપણે જેના આકાર સમાન હોય તેવી આકૃતિઓ વિશે અભ્યાસ કરીશું. પરંતુ તેમના કદ સમાન હોય તે જરૂરી નથી. જે બે આકૃતિઓના આકાર સમાન હોય (કદ સમાન હોય તે જરૂરી નથી) તેમને સમરૂપ આકૃતિઓ કહે છે. ખાસ કરીને, આપણે બે ત્રિકોણની સમરૂપતાની ચર્ચા કરીશું.
→ તમે જાણો છો તેમ એકરૂપ આકૃતિઓ દર્શાવવા માટે સંકેત ≅ વપરાય છે. તે જ રીતે સમરૂપ આકૃતિઓ દર્શાવવા માટે સંકેત ~ વપરાય છે અને તેનો અર્થ “ને સમરૂપ છે’ થાય.
→ બે એકરૂપ આકૃતિઓ એકબીજાને બરાબર બંધબેસતી થાય છે. બીજા શબ્દોમાં, બે એકરૂપ આકૃતિઓ પૈકી કોઈ પણ એક આકૃતિને બીજી આકૃતિ પર મૂકવાથી તેઓ એકબીજાને બરાબર ઢાંકે છે. સમરૂપ આકૃતિઓમાં તેવું થતું નથી. બે સમરૂપ આકૃતિઓના કદ સરખા ન હોવાથી પ્રત્યેક આકૃતિ બીજી આકૃતિને બરાબર ઢાંકે તે શક્ય નથી. પરંતુ સમરૂપ આકૃતિઓમાં પ્રત્યેક આકૃતિનો પડછાયો, મોટો અથવા નાનો, બીજી આકૃતિને બરાબર ઢાંકે છે.
![]()
→ સમરૂપ આકૃતિઓઃ કોઈ પણ બે રેખાખંડ હંમેશાં સમરૂપ હોય છે, પરંતુ તેઓ એકરૂપ હોય તે આવશ્યક નથી. બે રેખાખંડની લંબાઈ સરખી હોય, તો જ તેઓ એકરૂપ થાય.
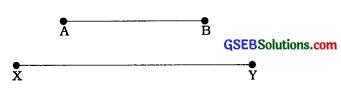
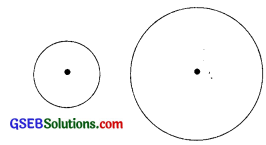
→ કોઈ પણ બે વર્તુળ હંમેશાં સમરૂપ છે.
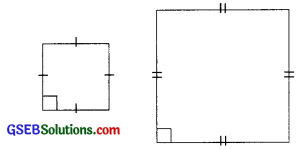
→ કોઈ પણ બે ચોરસ હંમેશાં સમરૂપ છે.
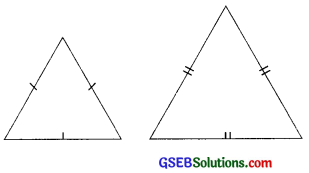
→ ક કોઈ પણ બે સમભુજ ત્રિકોણ હંમેશાં સમરૂપ છે.
→ સમરૂપ બહુકોણ : જો
- સમાન બાજુવાળા બહુકોણના અનુરૂપ ખૂણાઓ સમાન હોય અને
- તેમની અનુરૂપ બાજુઓના ગુણોત્તર સમાન હોય (કે બાજુઓ સમપ્રમાણમાં હોય), તો તે બહુકોણો સમરૂપ છે.
બહુકોણ માટે સંગત બાજુઓના ગુણોત્તરને સ્કેલમાપન (નિર્દેશક અપૂર્ણાક) કહેવામાં આવે છે.
→ બે બહુકોણની સમરૂપતા માટેની ઉપર દર્શાવતી બે શરતો (1) અને (2) પૈકી કોઈ એક જ શરત ત્રણથી વધુ બાજુઓ ધરાવતા બહુકોણોને સમરૂપ બનાવવા માટે પર્યાપ્ત નથી. આમ, ત્રણથી વધુ બાજુઓ ધરાવતા બહુકોણો માટે ઉપરની બે શરતો સ્વતંત્ર નથી. બીજા શબ્દોમાં, જો બે બહુકોણના અનુરૂપ ખૂણાઓ એકરૂપ (સમાન) હોય પરંતુ અનુરૂપ બાજુઓના ગુણોત્તર સમાન ન હોય, તો તે બે બહુકોણ સમરૂપ ન થાય. તે જ રીતે, જો બે બહુકોણની અનુરૂપ બાજુઓના ગુણોત્તર સમાન હોય પરંતુ અનુરૂપ ખૂણાઓ સમાન ન હોય, તો તે બહુકોણ સમરૂપ ન થાય.
→ ત્રણ બાજુઓ ધરાવતા બહુકોણ, એટલે કે, ત્રિકોણ માટે આ બંને શરતો સ્વતંત્ર છે. એટલે કે, એક શરતનું પાલન થાય તો બીજી શરતનું પાલન આપોઆપ થાય છે.
![]()
→ એક ચોરસ અને એક લંબચોરસ માટે તેમના બધા જ અનુરૂપ ખૂણાઓ સમાન હોય છે, પરંતુ અનુરૂપ બાજુઓના ગુણોત્તર સમાન ન હોવાથી એક ચોરસ અને એક લંબચોરસ કદી સમરૂપ ન થાય. તે જ પ્રમાણે એક ચોરસ અને એક સમબાજુ ચતુષ્કોણ માટે તેમની અનુરૂપ બાજુઓના ગુણોત્તર સમાન થાય પરંતુ અનુરૂપ ખૂણાઓ સમાન ન હોવાથી એક ચોરસ અને એક સમબાજુ ચતુષ્કોણ કદી સમરૂપ ન થાય.
→ અગત્યની નોંધ: ભૂમિતિનાં પ્રકરણો, ત્રિકોણમિતિનાં પ્રકરણો તથા પૃષ્ઠફળ અને ઘનફળનાં પ્રકરણોમાં આપેલ બધી જ આકૃતિઓ ફક્ત માર્ગદર્શન માટે જ છે. તે આકૃતિઓ ચોક્કસ માપ મુજબ દોરવામાં આવેલ નથી.
→ ત્રિકોણની સમરૂપતાઃ ક વ્યાખ્યા જો
- બે ત્રિકોણના અનુરૂપ ખૂણાઓ સમાન હોય
- તેમની અનુરૂપ બાજુઓના ગુણોત્તર સમાન હોય (એટલે કે બાજુઓ સમપ્રમાણમાં હોય),
→ તે બે ત્રિકોણો સમરૂપ છે. : બે સમકોણિક ત્રિકોણોમાં બે અનુરૂપ બાજુઓનો ગુણોત્તર સમાન હોય છે. આમ, સમરૂપ ત્રિકોણોની વ્યાખ્યાના બંને ભાગ એકલા પણ પર્યાપ્ત છે.
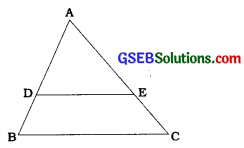
→ (સમપ્રમાણતાનું મૂળભૂત પ્રમેય (BPT) અથવા થેલ્સનું પ્રમેય): જો ત્રિકોણની કોઈ એક બાજુને સમાંતર દોરેલી રેખા બાકીની બે બાજુઓને ભિન્ન બિંદુઓમાં છેદે, તો તે બાજુઓ પર કપાતા રેખાખંડો તે બાજુઓનું સમપ્રમાણમાં વિભાજન કરે છે.
→ ΔABCમાં બાજુ BCને સમાંતર એક રેખા DE એ AB અને ACને અનુક્રમે D અને Eમાં છેદે છે, તો \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)
→ ગુણોત્તર અને પ્રમાણમાં કેટલાંક અગત્યનાં પરિણામ:

→ ગુણોત્તર અને પ્રમાણનાં પરિણામોની મદદથી થેલ્સના પ્રમેય પરથી નીચેનાં પરિણામો સહેલાઈથી સાબિત થાય :
\(\frac{\mathrm{AD}}{\mathrm{AB}}=\frac{\mathrm{AE}}{\mathrm{AC}}\) અને \(\frac{\mathrm{DB}}{\mathrm{AB}}=\frac{\mathrm{EC}}{\mathrm{AC}}\)
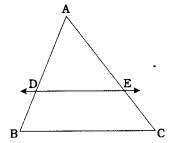
→ થેલ્સનું પ્રમેય એટલે કે BPTનું પ્રતીપ પ્રમેય જો કોઈ રેખા ત્રિકોણની બે બાજુઓનું સમાન ગુણોત્તરમાં વિભાજન કરે, તો તે રેખા ત્રીજી બાજુને સમાંતર હોય છે. જો કોઈ રેખા DE એ AABCની બાજુઓ AB અને ACને અનુક્રમે D અને Eમાં એવી રીતે છેદે કે જેથી \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\) થાય, તો રેખા DE એ બાજુ BCને સમાંતર હોય.
→ ત્રિકોણની સમરૂપતાનો સિદ્ધાંત સમરૂપ ત્રિકોણીની વ્યાખ્યા અનુસાર ΔABC અને ΔDEF એ સંગતતા ABC ↔ DEF માટે સમરૂપ થાય તે માટે નીચેની શરતોનું પાલન થવું જોઈએ:
- ∠A = ∠D, ∠B = ∠E, ∠C = ∠F અને
- \(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{EF}}=\frac{\mathrm{CA}}{\mathrm{FD}}\)
જો આ શરતોનું પાલન થતું હોય, તો આપણે સંકેતમાં લખી શકીએ કે ΔABC ~ ΔDEF અને તેને ત્રિકોણ ABC સમરૂપ ત્રિકોણ DEF એમ વાંચીશું.
→ બે ત્રિકોણની સમરૂપતાને તેનાં શિરોબિંદુઓની સાચી સંગતતાના સંકેતમાં દર્શાવીને અભિવ્યક્ત કરવી જોઈએ. જો ΔABC અને ΔDEFની ફક્ત એક જ સંગતતા ABC ↔ DEF સમરૂપતા હોય, તો તેને ફક્ત ΔABC ~ ΔDER લખી શકાય. ΔABC ~ ΔEDF અથવા ΔABC ~ ΔFDE લખવું ખોટું છે. પરંતુ, જો પહેલા ત્રિકોણનાં શિરોબિંદુઓના ક્રમમાં ફેરફાર કરીએ, તો તે જ પ્રકારનો ફેરફાર બીજા ત્રિકોણનાં શિરોબિંદુઓના ક્રમમાં કરીને લખી શકાય. એટલે કે, ΔABC ~ ΔDEFને ΔBAC ~ ΔEDF અથવા ΔCAB ~ ΔFDE પણ લખી શકાય.
→ ધોરણ IXમાં આપણે ત્રિકોણની એકરૂપતા માટેના કેટલાક સિદ્ધાંતો ભણી ચૂક્યા છીએ, જેમાં બે ત્રિકોણોના અનુરૂપ ભાગોની ફક્ત ત્રણ જોડ સમાયેલી હતી. તેવી જ રીતે, ત્રિકોણની સમરૂપતાના પણ કેટલાક સિદ્ધાંતો હવે આપણે જોઈશું જેમાં બે ત્રિકોણોના ફક્ત અમુક નિશ્ચિત ભાગો દ્વારા સમરૂપતા સાબિત થઈ શકે અને વ્યાખ્યા મુજબ બધાં જ છ અંગો પરની શરતનું પાલન કરવું ન પડે.
→ ખૂખૂણ્ શરત: જો બે ત્રિકોણોમાં અનુરૂપ ખૂણાઓ સમાન હોય, તો તેમની અનુરૂપ બાજુઓની જોડના ગુણોત્તર સમાન હોય (અથવા બાજુઓ સમપ્રમાણમાં હોય) અને તેથી તે બે ત્રિકોણો સમરૂપ છે. આ શરત બે ત્રિકોણની સમરૂપતા માટેની ખૂબૃખ ખૂણો-ખૂણોખૂણો) શરત તરીકે ઓળખાય છે.
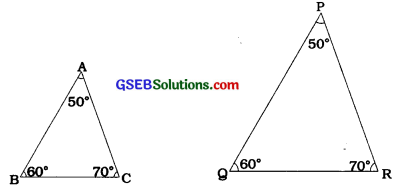
ΔABCમાં, ∠A = 50°, ∠B = 60° અને ∠C = 70°.
ΔPQRમાં, ∠P = 50°, ∠Q = 60° અને ∠R = 70°.
આથી ખૂખૂબૂ શરત મુજબ, ΔABC ~ ΔPOR.
→ ખૂણ્ શરતઃ જો કોઈ એક ત્રિકોણના બે ખૂણાઓ અનુક્રમે બીજા ત્રિકોણના બે ખૂણાઓને સમાન હોય, તો બે ત્રિકોણો સમરૂપ છે. તેને બે ત્રિકોણો માટેની સમરૂપતાની ખૂબૂ શરત તરીકે ઓળખવામાં આવે છે.
→ બાબાબા શરતઃ જો બે ત્રિકોણોમાં, એક ત્રિકોણની બાજુઓ બીજા ત્રિકોણની અનુરૂપ બાજુઓના સમપ્રમાણમાં હોય (એટલે કે ગુણોત્તરો સમાન હોય), તો તેમના અનુરૂપ ખૂણાઓ સમાન હોય અને તેથી બે ત્રિકોણો સમરૂપ હોય.
![]()
→ આ શરત બે ત્રિકોણો માટે બાબાબા (બાજુ-બાજુ-બાજુ) શરત તરીકે ઓળખાય છે.
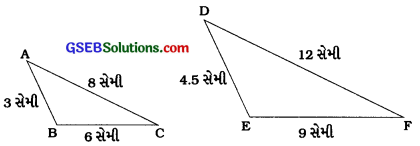
ΔABC અને ΔDEFમાં
\(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{EF}}=\frac{\mathrm{CA}}{\mathrm{FD}}=\frac{2}{3}\)
આથી બાબાબા શરત મુજબ, ΔBC ~ ΔDEF.
→ નોંધઃ તમને યાદ હશે કે બે બહુકોણી સમરૂપ છે તે માટે બે શરતો પૈકી કોઈ એક
- અનુરૂપ ખૂણાઓ સમાન છે.
- અનુરૂપ બાજુઓના ગુણોત્તર સમાન છે તે પર્યાપ્ત નથી. તેમ છતાં આધારે તમે હવે કહી શકશો કે બે ત્રિકોણની સમરૂપતા દર્શાવવા માટે બંને શરતો ચકાસવી જરૂરી નથી. તેમાં એક શરત પરથી બીજી શરત સિદ્ધ થાય.
→ બાખૂબી શરતઃ જો કોઈ ત્રિકોણનો એક ખૂણો બીજા ત્રિકોણના એક ખૂણાને સમાન હોય અને આ ખૂણાઓ જે બાજુઓને અંતર્ગત હોય તે બાજુઓ સમપ્રમાણમાં હોય, તો બે ત્રિકોણો સમરૂપ છે. * આ શરત બે ત્રિકોણની સમરૂપતા માટેના બાખૂબા (બાજુ ખૂણો-બાજુ) શરત (નિયમ) તરીકે ઓળખાય છે.
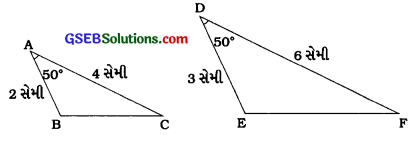
ΔABC અને ΔDEF, \(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{AC}}{\mathrm{DF}}=\frac{2}{3}\)
તથા ∠A = ∠D = 50°.
આથી બાખૂબા શરત મુજબ, ΔABC ~ ΔDEF.
→ બાખૂબ શરતનો એક મહત્ત્વનો પાસો: બે કાટકોણ ત્રિકોણોમાં, જો એક ત્રિકોણનો કર્ણ અને એક બાજુ બીજા ત્રિકોણના કર્ણ અને એક બાજુના ગુણોત્તર સમાન હોય, તો તે બે ત્રિકોણો સમરૂપ થાય. અહીં, સમાન કાટખૂણા એ કર્ણ અને બાજુની અંતર્ગત નથી. આ શરતને કાકબા શરત તરીકે ઓળખવામાં આવે છે.
→ સમરૂપ ત્રિકોણો આધારિત કેટલાક અગત્યના ગુણધર્મો :
(1) જો બે ત્રિકોણ સમરૂપ હોય, તો તેમની પરિમિતિઓનો ગુણોત્તર તેમની અનુરૂપ બાજુઓના ગુણોત્તર જેટલો જ હોય છે.
જો ΔABC ~ ΔDEF, તો

(2) બે સમરૂપ ત્રિકોણોની અનુરૂપ મધ્યગાઓ અનુરૂપ બાજુઓને સમપ્રમાણ હોય છે.
(3) બે સમરૂપ ત્રિકોણોના અનુરૂપ વેધોનો ગુણોત્તર અનુરૂપ બાજુઓના ગુણોત્તર જેટલો જ હોય છે.
(4) કોઈ પણ ત્રિકોણમાં, કોઈ પણ ખૂણાનો દ્વિભાજક તે ખૂણાની સામેની બાજુઓને જે રેખાખંડોમાં વિભાજિત કરે, તે રેખાખંડોનો ગુણોત્તર અને તે ખૂણાને સમાવતી ત્રિકોણની સંલગ્ન બાજુઓનો ગુણોત્તર સમાન હોય છે. ΔABCમાં, ∠Aનો દ્વિભાજક BCને Dમાં છેદે છે, તો \(\frac{\mathrm{BD}}{\mathrm{DC}}=\frac{\mathrm{AB}}{\mathrm{AC}}\)
(5) ΔABCમાં, જો AD મધ્યગા હોય, તો AB2 + AC2 = 2 (AD2 + BD2).
(6) બે સમરૂપ ત્રિકોણોના અનુરૂપ ખૂણાઓના દ્વિભાજકોના ત્રિકોણમાં સમાતા રેખાખંડોનો ગુણોત્તર ત્રિકોણની અનુરૂપ બાજુઓના ગુણોત્તર જેટલો જ હોય છે.
![]()
→ સમરૂપ ત્રિકોણોનાં ક્ષેત્રફળ : બે સમરૂપ ત્રિકોણોના ક્ષેત્રફળનો ગુણોત્તર તેમની અનુરૂપ બાજુઓના ગુણોત્તરના વર્ગ બરાબર હોય છે. બીજા શબ્દોમાં, જો ΔABC ~ ΔPOR હોય, તો
\(\frac{\mathrm{ABC}}{\mathrm{PQR}}=\left(\frac{\mathrm{AB}}{\mathrm{PQ}}\right)^{2}=\left(\frac{\mathrm{BC}}{\mathrm{gR}}\right)^{2}=\left(\frac{\mathrm{CA}}{\mathrm{RP}}\right)^{2}\)
નોંધ: ΔABCના ક્ષેત્રફળ માટે ધોરણ દર્શાવવામાં આવે છે. માં ar(ABC) સંકેત વાપરેલ છે જ. તદ્દુપરાંત, ΔABCના ક્ષેત્રફળને ABC દ્વારા પણ
→ પાયથાગોરસ પ્રમેય : જો કાટકોણ ત્રિકોણમાં કાટખૂણો બનાવતા શિરોબિંદુથી કર્ણ પર વેધ દોરેલ હોય, તો વેધની બંને તરફના ત્રિકોણો મૂળ ત્રિકોણને સમરૂપ હોય છે અને એકબીજાને સમરૂપ હોય છે. ΔABCમાં, ∠B = 90° અને BM વેધ છે,
તો Δ AMB ~ ΔBMC ~ ΔABC
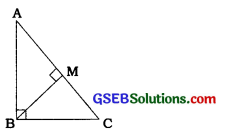
→ પરથી નીચેના અગત્યના પરિણામો મળે છે?
ΔAMB ~ ΔBMC
∴ \(\frac{\mathrm{BM}}{\mathrm{CM}}=\frac{\mathrm{AM}}{\mathrm{BM}}\)
∴ BM2 = AM. CM
ΔAMB ~ ΔABC
∴\(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\mathrm{AM}}{\mathrm{AB}}\)
∴ AB2 = AM. AC
ΔBMC ~ ΔABC
∴ \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{\mathrm{CM}}{\mathrm{BC}}\)
∴ BC2 = CM. AC
AM અને CMને અનુક્રમે AB અને BCના સંલગ્ન રેખાખંડ કહેવામાં આવે છે. તેઓ કર્ણના રેખાખંડ છે.
→ (પાયથાગોરસ પ્રમેય) કાટકોણ ત્રિકોણમાં, કર્ણનો વર્ગ બાકીની બે બાજુઓના વર્ગોના સરવાળા જેટલો હોય છે.
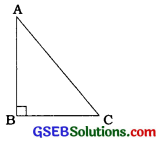
ΔABCમાં, જો AB = 90°, તો AB2 + BC2 = AC2.
→ આમ, જો કાટકોણ ત્રિકોણની કોઈ પણ બે બાજઓ જાણતા હોઈએ, તો ત્રીજી બાજુ સરળતાથી શોધી શકાય છે. જ કાટકોણ ત્રિકોણમાં કર્ણ સૌથી મોટી બાજુ છે.
→ કાટકોણ ત્રિકોણના કેટલાક ગુણધર્મો
- કાટકોણ ત્રિકોણમાં કર્ણ પરની મધ્યગાની લંબાઈ કર્ણની લંબાઈથી અડધી હોય છે.
- સમદ્વિબાજુ કાટકોણ ત્રિકોણમાં કર્ણનું માપ બાકીની દરેક બાજુના માપથી √2 ગણું હોય છે.
- કાટકોણ ત્રિકોણમાં જો કોઈ લઘુકોણનું માપ 30° હોય, તો તેની સામેની બાજુનું માપ કર્ણના માપ કરતાં અડધું હોય છે.
→ પાયથાગોરિયન ત્રિપુટીઓ કાટકોણ ત્રિકોણની બાજુઓનાં માપ દર્શાવતી ત્રિપુટી(ત્રય)ને પાયથાગોરિયન ત્રિપુટી કહે છે. 100થી નાના પૂર્ણાકો દ્વારા મળતી પાયથાગોરિયન ત્રિપુટીઓ નીચે મુજબ છેઃ

→ સામાન્યતઃ ΔABCમાં,
- ∠Aની સામેની બાજુ BCના માપને વ દ્વારા,
- ∠Bની સામેની બાજુ ACના માપને b દ્વારા તથા
- ∠Cની સામેની બાજુ ABના માપને C દ્વારા દર્શાવાય છે.
→ પાયથાગોરસ પ્રમેયનું પ્રતીપ) : ત્રિકોણમાં જો કોઈ એક બાજુનો વર્ગ, બાકીની બે બાજુઓના વર્ગોના સરવાળા બરાબર હોય, તો પહેલી બાજુની સામેનો ખૂણો કાટખૂણો હોય.
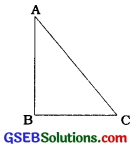
ΔABCમાં, જો AC2 = AB2 + BC2, તો ∠B કાટખૂણો છે.
→ ધારો કે ΔABCમાં AC એ સૌથી મોટી બાજુ છેઃ
- જો AC2 = AB2 + BC2, તો ∠B = 90° અને ABC કાટકોણ ત્રિકોણ છે.
- જો AC2 > AB2 + 2, તો ∠B > 90° અને ABC ગુરુકોણ ત્રિકોણ છે.
- જો AC2 < AB2 + BC2, તો ∠B < 90° અને AABC લઘુકોણ ત્રિકોણ છે.
→ પાયથાગોરસ પ્રમેય પર આધારિત કેટલાંક અગત્યના પરિણામો :
- ΔABCમાં, જો AD મધ્યગા હોય, તો AB2 + AC2 = 2(AD2 + BD2).
- ΔABCમાં, જો AD, BE અને CP મધ્યગાઓ હોય, તો 3(AB2 + BC2 + CA2) = 4 (AD2 + BE2 + CF2).
- ΔABCમાં, જો ∠B ગુરુકોણ હોય તથા AD વેધ હોય, તો AC2 = AB2 + BC2 + 2 BC × BD.
- ΔABCમાં, જો ∠B લઘુકોણ હોય તથા AD વેધ હોય, તો AC2 = AB2 + BC2 – 2 BC × BD.
→ સમાન આકાર ધરાવતી, પરંતુ જેના માટે સમાન કદ હોય તે જરૂરી નથી તેવી બે આકૃતિઓને સમરૂપ આકૃતિઓ કહે છે. જ બધી એકરૂપ આકૃતિઓ સમરૂપ છે, પરંતુ પ્રતીપ સાચું નથી.
- કોઈ બહુકોણના અનુરૂપ ખૂણાઓ સમાન હોય અને
- તેમની અનુરૂપ બાજુઓના ગુણોત્તર સમાન હોય (એટલે કે સમપ્રમાણમાં હોય) તો સમાન સંખ્યામાં બાજુઓવાળા બે બહુકોણ સમરૂપ છે. કે જો કોઈ ત્રિકોણની એક બાજુને સમાંતર દોરેલી રેખા, બાકીની બે બાજુઓને ભિન્ન બિંદુઓમાં છે, તો બાજુઓનું સમાન ગુણોત્તરમાં વિભાજન થાય છે.
![]()
→ જો કોઈ રેખા ત્રિકોણની બે બાજુઓનું સમાન ગુણોત્તરમાં વિભાજન કરે, તો તે રેખા ત્રીજી બાજુને સમાંતર હોય.
→ જો બે ત્રિકોણોમાં અનુરૂપ ખૂણાઓ સમાન હોય, તો અનુરૂપ બાજુઓના ગુણોત્તરો સમાન હોય, તો બે ત્રિકોણો સમરૂપ હોય (ખૂખૂખૂ- સમરૂપતા).
→ જો બે ત્રિકોણોમાં, એક ત્રિકોણના બે ખૂણાઓ અનુક્રમે બીજા ત્રિકોણના બે ખૂણાઓને સમાન હોય, અને તેથી તે બે ત્રિકોણો સમરૂપ છે (ખૂબૃ સમરૂપતા).
→ જો બે ત્રિકોણોમાં અનુરૂપ બાજુઓ સમપ્રમાણમાં હોય તો તેમના અનુરૂપ ખૂણાઓ સમાન હોય અને તેથી ત્રિકોણો સમરૂપ છે (બાબાબા સમરૂપતા).
→ જો કોઈ ત્રિકોણનો એક ખૂણો બીજા ત્રિકોણના એક ખૂણાને સમાન હોય અને આ ખૂણાઓ જે બાજુઓને અંતર્ગત હોય તે સમપ્રમાણમાં હોય, તો બે ત્રિકોણી સમરૂપ છે (બાખૂબા સમરૂપતા).
→ બે સમરૂપ ત્રિકોણોનાં ક્ષેત્રફળોનો ગુણોત્તર તેમની અનુરૂપ બાજુઓના ગુણોત્તરના વર્ગ જેટલો હોય છે.
→ જો કાટકોણ ત્રિકોણના કાટખૂણાના શિરોબિંદુમાંથી કર્ણ પર વેધ દોરવામાં આવે, તો વેધની બંને તરફના ત્રિકોણો મૂળ ત્રિકોણને તેમજ એકબીજાને સમરૂપ હોય છે.
→ કાટકોણ ત્રિકોણમાં, કર્ણનો વર્ગ બાકીની બે બાજુઓના વર્ગોના સરવાળા જેટલો હોય છે. (પાયથાગોરસ પ્રમેય)
→ જો ત્રિકોણમાં કોઈ એક બાજુનો વર્ગ બાકીની બે બાજુઓના વર્ગના સરવાળા જેટલો હોય, તો પહેલી બાજુની સામેનો ખૂણો કાટખૂણો હોય.
→ સમરૂપ ત્રિકોણોમાં અનુરૂપ મધ્યગાઓનો ગુણોત્તર, અનુરૂપ વેધોનો ગુણોત્તર તથા અનુરૂપ ખૂણાઓના દ્વિભાજકોના ત્રિકોણમાં સમાતા રેખાખંડોનો ગુણોત્તર ત્રિકોણની અનુરૂપ બાજુઓના ગુણોત્તર જેટલો જ હોય છે.
→ ΔABCમાં, જો ∠Aનો દ્વિભાજક BCને Dમાં છેદે, તો
\(\frac{\mathrm{BD}}{\mathrm{DC}}=\frac{\mathrm{AB}}{\mathrm{AC}}\)
→ ΔABCમાં, જો AD મધ્યગા હોય, તો AB2 + AC2 = 2 (AD2 + BD2).
→ સમલંબ ચતુષ્કોણના વિકર્ણો પરસ્પરનું સમાન ગુણોત્તરમાં વિભાજન કરે છે.