GSEB Class 10 Maths Notes Chapter 8 ત્રિકોણમિતિનો પરિચય

This GSEB Class 10 Maths Notes Chapter 8 ત્રિકોણમિતિનો પરિચય covers all the important topics and concepts as mentioned in the chapter.

ત્રિકોણમિતિનો પરિચય Class 10 GSEB Notes

→ પ્રાસ્તાવિક : ત્રિકોણમિતિ (Trigonometry) : ત્રિકોણમિતિ એ ગણિતની એક મહત્ત્વની શાખા છે. અંગ્રેજી શબ્દ Trigonometry ત્રણ ગ્રીક શબ્દો “Tri’ (એટલે કે ત્રણ), ‘Gon’ (એટલે કે બાજુ) અને ‘Metron” (એટલે કે માપ)ના સંયોજનથી બનેલ છે. ખરેખર તો ત્રિકોણમિતિ, ત્રિકોણની બાજુઓ તથા ખૂણાઓ વચ્ચેના સંબંધનો અભ્યાસ છે.

→ આ પ્રકરણમાં આપણે કાટકોણ ત્રિકોણના લઘુકોણોની સાપેક્ષમાં રહેલી ત્રિકોણની બાજુઓના ગુણોત્તરો વિશે ચર્ચા કરીશું. આપણે તેને ખૂણાઓ માટેના ત્રિકોણમિતીય ગુણોત્તર કહીશું. આ ગુણોત્તરનો વિસ્તાર બીજા ખૂણાઓ માટે પણ કરી શકાય છે. છતાં પણ આપણે અહીં આપણી ચર્ચા ફક્ત લઘુકોણ સુધી જ સીમિત રાખીશું. આપણે અહીં 0° અને 90° માપના ખૂણાઓના ત્રિકોણમિતીય ગુણોત્તરો પણ વ્યાખ્યાયિત કરીશું તેમજ કેટલાક વિશિષ્ટ ખૂણાઓ માટેના ત્રિકોણમિતીય ગુણોત્તરો મેળવીશું.

→ ત્રિકોણમિતીય ગુણોત્તરો (Trigonometric ratios) :
આપણે કાટકોણ ત્રિકોણ ABC લઈએ, જેમાં ∠B કાટખૂણો છે. અહીં ∠CAB (∠A) અને ∠ACB (∠C) લઘુકોણ છે.

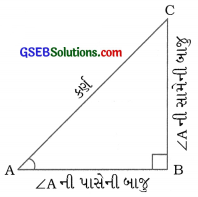
→ Δ ABCHI, AC એ કર્ણ(Hypotenuse) છે, BC એ ∠Aની સામેની બાજુ (Opposite side) છે તથા AB એ ∠ Aની પાસેની બાજુ (Adjacent side) છે.

→ તે જ રીતે, AC એ કર્ણ છે. AB એ ∠C ની સામેની બાજુ છે તથા BC એ ∠Cની પાસેની બાજુ છે.

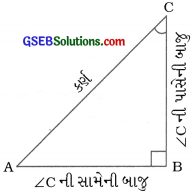
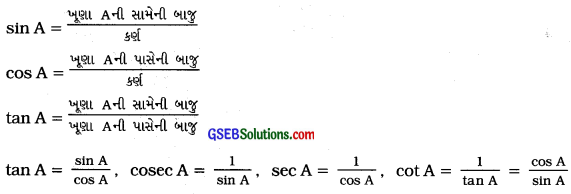
→ કાટકોણ ત્રિકોણ ABCમાં, ∠A માટેના ત્રિકોણમિતીય ગુણોત્તરો નીચે પ્રમાણે વ્યાખ્યાયિત કરાય છે:


ઉપરોક્ત વ્યાખ્યાયિત ગુણોત્તરોને ટૂંકમાં અનુક્રમે sin A, cos A, tan A, cosec A, sec A અને cot A સ્વરૂપે લખાય છે. ધ્યાન આપો, અહીં ગુણોત્તરો cosed A, sec A અને cot A અનુક્રમે sin A, cos A અને tan Aના વ્યસ્ત ગુણોત્તરો છે.

→ અહીં, તમે એ પણ જોઈ શકો છો કે,
tan A = \(\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{\frac{\mathrm{BC}}{\mathrm{AC}}}{\frac{\mathrm{AB}}{\mathrm{AC}}}=\frac{\sin \mathrm{A}}{\cos \mathrm{A}}\) અને cot A = \(\frac{\cos \mathrm{A}}{\sin \mathrm{A}}\).

→ આમ, કાટકોણ ત્રિકોણમાં રહેલા લઘુકોણના ત્રિકોણમિતીય ગુણોત્તરો, ત્રિકોણના ખૂણાઓ તથા બાજુઓની લંબાઈ વચ્ચેનો સંબંધ દર્શાવે છે. ધ્યાન આપો, અહીં sin Aનો ઉપયોગ ‘ખૂણા Aના sin’ના સંક્ષિપ્ત રૂપે કરવામાં આવેલ છે. sin A એ sin અને Aનો ગુણાકાર નથી. sinને Aથી અલગ કરીએ તો તેનો કોઈ જ અર્થ નથી. તે જ પ્રમાણે cos A એ cos અને Aનો ગુણાકાર નથી. તેવી જ રીતે બીજા ગુણોત્તરો માટે પણ આવું જ અર્થઘટન કરી શકાય.

→ દરેક ત્રિકોણમિતીય ગુણોત્તર કોઈ વાસ્તવિક સંખ્યા છે. તેનો કોઈ એકમ નથી.

→ આપણી સુવિધા માટે આપણે (sin A)²ના બદલે sin² A, (cos A)³ના બદલે cos³A, (tan A)⁶ના બદલે tan⁶A વગેરે વાપરીશું.

→ પરંતુ, sec A = \(\frac{1}{\cos \mathrm{A}}\) = (cos A)^-1ના બદલે cos^-1A ન લખી શકાય.

→ ત્રિકોણમિતિમાં આપણે કેટલીક વાર ગ્રીક અક્ષરો છે θ(થીટા), α (આલ્ફા), β (બીટા), γ (ગમા), Φ (ફાઈ) વગેરેનો ઉપયોગ પણ ખૂણો દર્શાવવા માટે કરીએ છીએ.

→ ત્રિકોણમિતીય ગુણોત્તરના સંબંધો (The relations of trigonometric ratids) :

• tan A = \(\frac{\sin A}{\cos A}\)
• cot A = \(\frac{\cosn A}{\sin A}\)
• cosec A = \(\frac{1}{\sin A}\)
• sec A = \(\frac{1}{\cos A}\)
• tan A. cotA = 1
• sec A cos A = 1
• cosec A·sin A = 1

→ ત્રિકોણમિતીય ગુણોત્તરની અવિચલતા (Invariance of trigonometric ratio) : હવે, કાટકોણ ત્રિકોણ ABCના કર્ણ AC પર બિંદુ ? અને લંબાવેલ AC પર બિંદુ Q લો. વળી, PM ⊥ AB તથા QN ⊥ લંબાવેલ AB દોરો. ખૂબૂ શરત અનુસાર, ΔABC ~ ΔAMP ~ ΔANQ થાય.

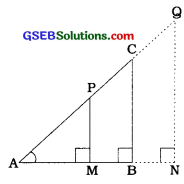
∴ \(\frac{\mathrm{BC}}{\mathrm{MP}}=\frac{\mathrm{AC}}{\mathrm{AP}}\) અને \(\frac{\mathrm{BC}}{\mathrm{NQ}}=\frac{\mathrm{AC}}{\mathrm{AQ}}\)

∴\(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{\mathrm{MP}}{\mathrm{AP}}\) અને \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{\mathrm{NQ}}{\mathrm{AQ}}\)

→ આથી Δ ABCમાં sin A = Δ AMPમાં sin A અને
Δ ABCમાં sin A = Δ ANQમાં sin A.

→ ટૂંકમાં, ત્રિકોણની બાજુઓનાં માપમાં પરિવર્તન થાય તો પણ sin Aના મૂલ્યમાં કોઈ પણ પરિવર્તન થતું નથી.

→ આપણા આ અવલોકનથી સ્પષ્ટ થાય છે કે, જો ખૂણાનું માપ સમાન રહે, તો તે ખૂણા માટેના ત્રિકોણમિતીય ગુણોત્તરોનાં મૂલ્યોમાં ત્રિકોણની બાજુઓની લંબાઈ સાથે કોઈ પરિવર્તન થતું નથી.

→ જો કોઈ ખૂણાનો કોઈ પણ એક ત્રિકોણમિતીય ગુણોત્તર આપેલ
હોય (એટલે કે કાટકોણ ત્રિકોણની કોઈ પણ બે બાજુઓનો ગુણોત્તર આપેલ હોય), તો તે ખૂણાના બીજા બધા જ ત્રિકોણમિતીય ગુણોત્તરો પાયથાગોરસ પ્રમેયની મદદથી શોધી શકાય છે.

→ ΔABCમાં, ∠B = 90° અને sin A = \(\frac{1}{4}\) હોય, તો તે પરથી BC અને ACનો ગુણોત્તર 1: 4 મળે. આ સંજોગોમાં આપણે BC = k અને AC = 4k લઈ શકીએ,
જ્યાં k કોઈ ધન વાસ્તવિક સંખ્યા છે.

→ sin A તથા cos Aનું મૂલ્ય હંમેશાં 1 કરતાં ઓછું હોય છે. (Aની અમુક વિશિષ્ટ કિંમતો માટે તે મૂલ્ય 1 હોય છે.) sec A તથા cosec Aનું મૂલ્ય હંમેશાં 1થી અધિક હોય છે. (Aની અમુક વિશિષ્ટ કિંમતો માટે તે મૂલ્ય 1 હોય છે.) tan A તથા cot Aનું મૂલ્ય કોઈ પણ વાસ્તવિક સંખ્યા હોઈ શકે છે.

→ વિશિષ્ટ માપના ખૂણા માટેના ત્રિકોણમિતીય ગુણોત્તરોઃ 45° ના ખૂણા માટે ત્રિકોણમિતીય ગુણોત્તરો :

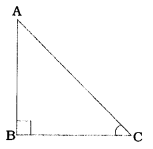
ΔABCમાં, ∠B = 90° અને ∠C = 45
હવે, ∠A = 180° – (90° + 45°) = 45
આથી ΔABCમાં, AB = BC.
ધારો. કે, AB = BC = a

હવે, પાયથાગોરસ પ્રમેય મુજબ,
AC² = AB² + BC² = a² + a² = 2a².
∴ AC = √2 a
હવે, ત્રિકોણમિતીય ગુણોત્તરની વ્યાખ્યા મુજબ,

→ 30° અને 80ના ખૂણા માટે ત્રિકોણમિતીય ગુણોત્તરોઃ

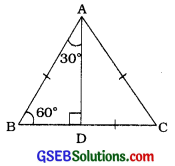
કોઈ એક સમબાજુ ત્રિકોણ ABC લો. ΔABC સમબાજુ ત્રિકોણ હોવાથી, ∠A = ∠B = ∠C = 60°

AD ⊥BC દોરો.
હવે, ΔADB અને ΔADCમાં,
∠ADB = ∠ADC (કાટખૂણા)
કર્ણ AB = કર્ણ AC (સમબાજુ ત્રિકોણ)
AD = AD (સમાન બાજુ)

∴કાકબા શરત મુજબ, ΔADB ≅ ΔADC
BD = CD અને ∠BAD = ∠CAD (CPCT)
પરંતુ, BD + CD = BC અને ∠BAD + ∠CAD = ∠A
BD = \(\frac{1}{2}\)BC અને
∠BAD = \(\frac{1}{2}\)∠A = \(\frac{1}{2}\)(60°) = 30°

ધારો. કે AB = BC = AC = 2a
આથી BD = \(\frac{1}{2}\)BC = a
આમ, ΔADBમાં, ∠D = 90°, ∠B = 60°, ∠A = 30°, AB = 2a 24 BD = a

હવે, પાયથાગોરસ પ્રમેય મુજબ, AD² = AB² – BD² = (2a)² – (a)² = 3a²
∴AD = √3a

હવે, ત્રિકોણમિતીય ગુણોત્તરોની વ્યાખ્યા મુજબ,

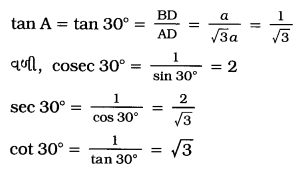
→ 0° અને 90° માટેના ત્રિકોણમિતીય ગુણોત્તર:

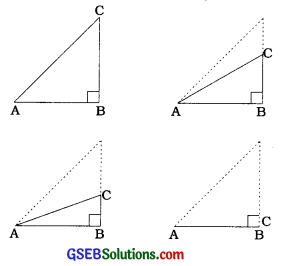
ઉપર આપેલ કાટકોણ ત્રિકોણ ABCની આકૃતિઓ પરથી સ્પષ્ટ છે કે, જેમ જેમ ∠Aનું માપ નાનું થતું જશે તેમ તેમ બાજુ BCની લંબાઈ ઘટતી જશે. બિંદુ C, બિંદુ Bની નજીક આવતું જશે અને જ્યારે ∠Aનું માપ 0°ની એકદમ નજીક હશે ત્યારે BC ની લંબાઈ શૂન્યની નજીક હશે અને AC લગભગ ABને સમાન થઈ જશે. આ પરથી આપણે sin 0° અને cos 0૧ના મૂલ્યોને વ્યાખ્યાયિત કરી શકીશું.
sin 0° = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{0}{\mathrm{AC}}\) = 0 અને cos O° = \(\frac{\mathrm{AB}}{\mathrm{AC}}\) = 1.

હવે, sin 0° = 0 અને cos 0° = 1 પરથી 0°ના ખૂણાના બીજા ત્રિકોણમિતીય ગુણોત્તરો નીચે પ્રમાણે મળે :

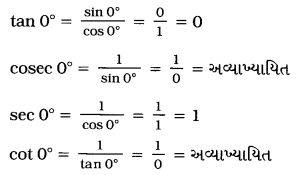
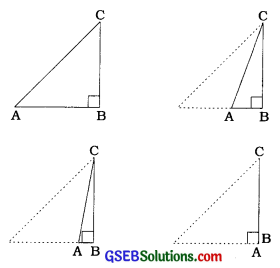
→ તે જ રીતે, જ્યારે ∠A નું માપ 90°ની એકદમ નજીક હશે ત્યારે ABની લંબાઈ શૂન્યની નજીક હશે અને AC લગભગ BCને સમાન થઈ જશે.
આ પરથી આપણે sin 90° અને cos 90નાં મૂલ્યોને વ્યાખ્યાયિત કરી શકીશું.
sin 90° = \(\frac{\mathrm{BC}}{\mathrm{AC}}\) = 1 અને cos 90° = AB = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{0}{\mathrm{AC}}\) = 0

→ હવે, sin 90° = 1 અને cos 90° = 0 પરથી 90°ના ખૂણાના બીજા ત્રિકોણમિતીય ગુણોત્તરો નીચે પ્રમાણે મળે :
tan 90° = \(\frac{\sin 90^{\circ}}{\cos 90^{\circ}}=\frac{1}{0}\) = અવ્યાખ્યાયિત
cosec 90° = \(\frac{1}{\sin 90^{\circ}}=\frac{1}{1}\) = 1
sec 90° = \(\frac{1}{\cos 90^{\circ}}=\frac{1}{0}\) = અવ્યાખ્યાયિત
cot 90° = \(\frac{\cos 90^{\circ}}{\sin 90^{\circ}}=\frac{0}{1}\) = = 0

→ હવે, આપણે 0°, 30°, 45, 60° અને 90ના ખૂણાના બધા જ ત્રિકોણમિતીય ગુણોત્તરોને નીચે દર્શાવેલ કોષ્ટક સ્વરૂપમાં મૂકી શકીએ:

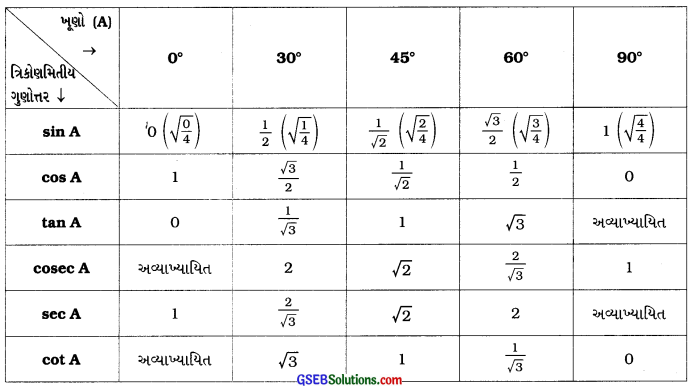
→ ઉપરોક્ત કોષ્ટકમાં તમે જોઈ શકો છો કે, જેમ જેમ ∠Aનું માપ 0થી વધીને 90° થાય છે, તેમ તેમ sin Aનું મૂલ્ય 0થી વધીને 1 થાય છે તથા cos Aનું મૂલ્ય 1થી ઘટીને 0 થાય છે. તઉપરાંત, tan Aનું મૂલ્ય પણ વધતું જાય છે પરંતુ તેના મૂલ્યમાં થતો વધારો sin Aના મૂલ્યમાં થતા વધારા કરતાં ઘણો વધારે હોય છે અને 90ના ખૂણા માટે તેનું મૂલ્ય અનંત થાય છે.

→ તમે અહીં જોઈ શકો છો કે, કાટકોણ ત્રિકોણમાં જો કોઈ એક બાજુ અને અન્ય કોઈ એક ભાગ (કોઈ એક લઘુકોણ અથવા તો કોઈ એક બાજુ) આપેલ હોય, તો ત્રિકોણની બાકીની બાજુ અને ખૂણાઓનાં માપ શોધી શકાય છે.

→ કોટિકોણના ત્રિકોણમિતીય ગુણોત્તરોઃ આ કોટિકોણ : જો બે ખૂણાઓનાં માપનો સરવાળો 90° હોય, તો બંને ખૂણાઓને એકબીજાના કોટિકોણ કહે છે.

→ કોઈ પણ કાટકોણ ત્રિકોણના લઘુકોણો કોટિકોણની જોડી બનાવે છે.

→ કોટિકોણના ત્રિકોણમિતીય ગુણોત્તરો વચ્ચેના સંબંધોઃ એવો એક કાટકોણ ત્રિકોણ ABC લઈએ, જેમાં ∠B કાટખૂણો હોય. ΔABCમાં, ∠B = 90°.

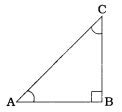
∴ ∠A + 20 = 180° – 90° = 90° AA . ∠C = 90° – ∠A

→ કોટિકોણની જોડ રચતા બંને ખૂણા હંમેશાં લઘુકોણ હોય છે. તેથી ઉપરોક્ત બધાં જ પરિણામો કોઈ પણ લઘુકોણ માટે સત્ય છે.

→ 0° અને 90°ના ખૂણાઓ માટે, tan 0° = 0 = cot 90°, sec 0° = 1 = cosec 90° તથા sec 90°, cosec 09, tan 90° અને cot O° અવ્યાખ્યાયિત છે.

→ ત્રિકોણમિતીય નિત્યસમોઃ બૈજિક નિત્યસમ જો બેજિક સમીકરણમાં આવતા ચલના દરેક મૂલ્ય માટે સમીકરણ સત્ય હોય, તો સમીકરણને નિત્યસમ કહે છે.

→ ત્રિકોણમિતીય નિત્યસમ જ્યારે ત્રિકોણમિતીય ગુણોત્તરોને સમાવતા સમીકરણમાં આવતા ખૂણાઓના પ્રત્યેક મૂલ્ય માટે સમીકરણ સત્ય હોય ત્યારે તે સમીકરણને ત્રિકોણમિતીય નિત્યસમ કહે છે.

→ ત્રિકોણમિતીય નિત્યસમ મેળવવા
જો AABCમાં ૮B કાટખૂણો હોય, તો AB² + BC² = AC² ….. (1)

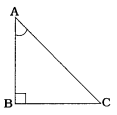
સમીકરણ (1)ના દરેક પદને AC² વડે ભાગતાં,
\(\frac{\mathrm{AB}^{2}}{\mathrm{AC}^{2}}+\frac{\mathrm{BC}^{2}}{\mathrm{AC}^{2}}=\frac{\mathrm{AC}^{2}}{\mathrm{AC}^{2}}\)
∴ \(\left(\frac{\mathrm{AB}}{\mathrm{AC}}\right)^{2}+\left(\frac{\mathrm{BC}}{\mathrm{AC}}\right)^{2}\) = 1
∴ (cos A)² + (sin A)² = 1
∴ cos²A + sin²A = 1 ………..(2)

સમીકરણ (1)ના દરેક પદને AB² વડે ભાગતાં,
\(\frac{\mathrm{AB}^{2}}{\mathrm{AB}^{2}}+\frac{\mathrm{BC}^{2}}{\mathrm{AB}^{2}}=\frac{\mathrm{AC}^{2}}{\mathrm{AB}^{2}}\)
∴ 1 + \(\left(\frac{\mathrm{BC}}{\mathrm{AB}}\right)^{2}=\left(\frac{\mathrm{AC}}{\mathrm{AB}}\right)^{2}\)
∴ 1+ (tanA)² = (sec A)²
∴ 1 + tan²A = sec²A ……. (3)

સમીકરણ (1)ના દરેક પદને BC2 વડે ભાગતાં,
∴ \(\frac{\mathrm{AB}^{2}}{\mathrm{AB}^{2}}+\frac{\mathrm{BC}^{2}}{\mathrm{AB}^{2}}=\frac{\mathrm{AC}^{2}}{\mathrm{AB}^{2}}\)
∴ \(\left(\frac{\mathrm{AB}}{\mathrm{BC}}\right)^{2}\) + 1 = \(\left(\frac{\mathrm{AC}}{\mathrm{BC}}\right)^{2}\)
∴ (cot A)² + 1 = (cosetA)²
∴ cot²A+ 1 = cosec² A … (4)

અહીં, (2), (૩) અને (4) એ ત્રિકોણમિતીય નિત્યસમ છે, કારણ કે તેઓ દરેક લઘુકોણ માટે સાચા છે અને જેના ત્રિકોણમિતીય – ગુણોત્તરી વ્યાખ્યાયિત છે તેવા દરેક ખૂણા માટે સાચા છે.

→ નિત્યસમ sin² θ + cos² θ = ને sin² θ = 1 – cos² θ
અને cos²θ = 1 – sin²θ સ્વરૂપમાં પણ દર્શાવી શકાય.

→ નિત્યસમ sec² θ = 1 + tan²θ ને sec²θ – tan² θ = 1
અને sec² θ = tan²θ સ્વરૂપમાં પણ દર્શાવી શકાય.

→ નિત્યસમ cosec²θ = 1 + cot²θ
cosec²θ – cot²θ = 1 અને cosec²θ – 1 = cot²θ સ્વરૂપમાં પણ દર્શાવી શકાય.

નોંધઃ આ નિત્યસમોના ઉપયોગથી દરેક ત્રિકોણમિતીય ગુણોત્તરને અન્ય ત્રિકોણમિતીય ગુણોત્તરના સ્વરૂપે દર્શાવી શકાય, જેમ કે,

આ પ્રકારના ઘણા નિત્યસમ મેળવી શકાય. આ દર્શાવે છે કે જો કોઈ એક ત્રિકોણમિતીય ગુણોત્તરની કિંમત જ્ઞાત હોય, તો અન્ય બધા જ ત્રિકોણમિતીય ગુણોત્તરોની કિંમત શોધી શકાય.

→ 1ને sec²θ – tan²θ અથવા cosec²θ – cot²θ સ્વરૂપે દર્શાવીને ઘણાં પરિણામો સહેલાઈથી સાબિત કરી શકાય છે.

→ sec²θ + cosec²θ = sec²θ .cosec²θ સહેલાઈથી સાબિત કરી શકાય છે.

→ જેમાં કાટખૂણો B હોય તેવા, કાટકોણ ત્રિકોણ ABCમાં,

→ જો આપણે કોઈ એક ત્રિકોણમિતીય ગુણોત્તરનું મૂલ્ય જાણતાં હોઈએ, તો અન્ય ત્રિકોણમિતીય ગુણોત્તરોનાં મૂલ્ય સરળતાથી શોધી શકાય છે.

→ 0°, 30°, 45°, 60° અને 90° માપના ખૂણાઓ માટેના ત્રિકોણમિતીય ગુણોત્તરોનાં મૂલ્ય હંમેશાં યાદ રાખવાં.

→ sin A અને cosAનું મૂલ્ય ક્યારેય 1થી વધારે ન હોય અને sec A અને cosec Aનું મૂલ્ય હંમેશાં 1 અથવા 1થી વધારે જ હોય.

→ sin (90° – A) = cos A, cos (90° –A) = sin A;
tan (90° – A) = cot A, cot (90° –A) = tan A;
sec (90° – A) = cosec A, cosec (90° – A) = sec A.

→ sin²A + cos²A = 1,

• 0° ≤ A ≤ 90° હોય તેવા પ્રત્યેક A માટે sec²A – tan²A = 1
• 0° ≤ A ≤ 90° હોય તેવા પ્રત્યેક A માટે cosec²A – cot²A = 1

→ ઉપરોક્ત નિત્યસમોનાં બીજા સ્વરૂપ નીચે પ્રમાણે મળે :

• sin²A = 1 – cos²A અને cos²A = 1 – sin²A
• tan²A = sec²A – 1 અને sec²A – tan²A = 1
• cot²A = cosec²A – 1 અને cosec²A – cot²A = 1