This GSEB Class 7 Maths Notes Chapter 2 Fractions and Decimals covers all the important topics and concepts as mentioned in the chapter.
Fractions and Decimals Class 7 GSEB Notes
Bhaskara-I was a 7th century mathematician. He was the first to write numbers in the Hindu decimal system with a circle for the zero. He gave a unique and remarkable rational approximation of the sine function in his commentary on Aryabhata’s work. He also wrote two astronomical works in the line of Aryabhata’s school, the Mahabhaskariya and the Laghubhaskariya.
1. Fraction: Fraction is a number that represents poart of a whole. \(\frac { 1 }{ 4 }\) represents the one part when whole is divided into four equal parts. 4 is called the denominator and 1 is called the numerator.
2. Proper fraction: A fraction whose numerator is less than its denominator, is called a proper fraction. For example \(\frac{1}{2}, \frac{3}{5}, \frac{3}{4}\) are all proper fractions.
3. Improper fraction: A fraction whose numerator is greater than its denominator is called an improper fraction. For example: \(\frac{5}{4}, \frac{7}{4}, \frac{9}{5}\)are all improper fractions.
4. Mixed fractions: A fraction which can be expressed as a sum of a natural number and a proper fraction is called a mixed fraction. For example:
1\(\frac{3}{4}\) = 1 + \(\frac{3}{4}\)
5. Like fractions: Fractions having the same denominators are called like fractions.
For Example. \(\frac{1}{9}, \frac{2}{9}, \frac{8}{9}\) are like fractions.
6. Unlike fractions : Fractions having different denominators are called unlike fractions.
For example: \(\frac{5}{8}, \frac{3}{5}, \frac{4}{7}\)are unlike fractions.
7. Decimal fraction: A fraction whose denominator is 10 or a power of 10 i.e. 10, 100, 1000, is called a decimal fraction
For Example: \(\frac{7}{10}, \frac{24}{100}, \frac{732}{1000}\) are decimal fractions.
8. Simple fractions: A fraction whose denominator is a number other than 10, 100, 1000,…………… is called a simple or vulgar fraction.
For example: \(\frac{7}{15}, \frac{4}{25}, \frac{2}{17}\) are vulgar fractions.
9. Equivalent fractions: Equivalent fractions represent same part of a whole.
For example: \(\frac{1}{2}, \frac{2}{4}, \frac{3}{6}\) are all equivalent fractions:
Note: An improper fraction can be expressed as a mixed fraction and vice-versa. For example:
\(\frac{15}{2}\) is an improper fraction also \(\frac{15}{2}\) = 7\(\frac{1}{2}\)
which is a mixed fraction.

Now consider 3\(\frac{2}{5}\) , which is a mixed fraction. It can also be written as \(\frac{(3 \times 5)+2}{5}=\frac{17}{5}\) an improper fraction.
![]()
Multiplication of Fractions
Multiplication of a fraction by a whole number. We know that multiplication means repeated addition. For example, 4 × 3 represents 4 times 3 i.e 3 + 3 + 3 + 3 = 12
Now, to multiply \(\frac{2}{9}\) with 4, we write \(\frac{2}{9}\) four times and then add, that is
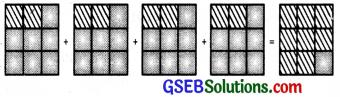
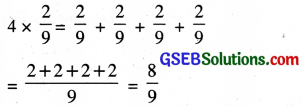
Thus to multiply a whole number with a proper or an improper fraction, we multiply the numerator of fraction with the whole number. After multiplication we get new numerator, where as the denominator in the product remains the same as in the given fraction.
Fraction as an operator ‘of’:
Observe the shaded portion of the circles in following figure. Each shaded portion represents \(\frac{1}{4}\) of 1.
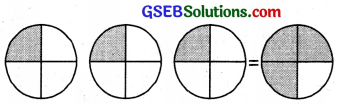
So, three shaded parts represents \(\frac{1}{4}\) of 3
After combining 3 shaded parts represent \(\frac{3}{4}\) of 1
So \(\frac{1}{4}\) of 3 = \(\frac{1}{4}\) × 3 = \(\frac{3}{4}\)
Thus, we observe that ‘of’ represent multiplication.
Multiplication of a Fraction by a Fraction
We know that multiplication also represents the operator ‘of’
So \(\frac{3}{4} \times \frac{1}{3}\) represents \(\frac{3}{4}\) of \(\frac{1}{3}\)
Let us now understand the meaning of \(\frac{3}{4}\) of \(\frac{1}{3}\) by following:
(i) \(\frac{1}{3}\) represents one part when the whole is three equal parts figure (a)

(a)
(ii) \(\frac{3}{4}\) of \(\frac{1}{3}\) represents the \(\frac{3}{4}\) of the shaded region figure (a)
(iii) To find \(\frac{3}{4}\) of \(\frac{1}{3}\) we divide each in four equal parts (figure) (b)
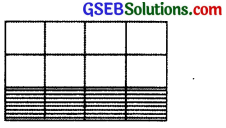
(b)
(iv) \(\frac{3}{4}\) of \(\frac{1}{3}\) is represented by double shaded region in figure (c)
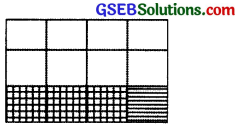
(c)
Value of the Products
(i) The value of the product of two proper fractions is smaller than each of the given fractions.
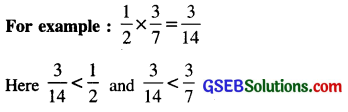
(ii) The value of the product of two improper fractions is greater than each of the given fractions.

(iii) The value of the product of a proper fraction and an improper fraction is less than the given improper fraction and greater than given the proper fraction.
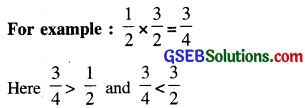
Division of Fractions
Reciprocal of a fraction. Reciprocal of a fraction is a fraction obtained by interchanging the places of numerator and denominator. The product of a fraction and its reciprocal is always ‘1’.
For example; The reciprocal of \(\frac{3}{7}\) is \(\frac{7}{3}\)
Also, we observe that, \(\frac{3}{7} \times \frac{7}{3}\) = 1
Hence. Fraction x reciprocal of fraction = 1
NOTE: Reciprocal of a fraction is also called multiplicative inverse of the fraction.
- Division of a whole number by a mixed fraction
- Division of a fraction by a non zero whole number
To divide a fraction by a non zero whole number, the fraction is multiplied by the reciprocal of whole number - Division of a fraction by another fraction To divide a fraction by another fraction, the first fraction is multiplied by the reciprocal of the second fraction.
Decimal Numbers
You have learnt about decimal numbers in the previous class that a fraction with denominators 10, 100,1000, ………. etc. can be expressed in another form, called decimal numbers. For example: In 23.715,23 is called whole number part and 715 is called decimal part.
![]()
Comparison of Decimal Numbers
To compare the two given decimal numbers, we first compare their whole number parts. The decimal number with the greater whole number part is greater of the two given decimals.
If the whole number parts are equal, then we compare the digits on the right side of the decimal point starting from the tenth place. If the digit at the tenth place are equal, we compare the digits at the hundredth place and so on.
While converting lower units of length, weight, height and money to their higher units, we are required to use decimals.
Multiplication of Decimal Numbers
Let us find 11.34 × 2.3
1134 × 23 = \(\frac{1134}{100} \times \frac{23}{10}=\frac{26082}{1000}\) = 26.082
In the above example, we converted the decimal numbers into fractions, multiplied the fractions and finally converted the product into decimal number.
But there are quicker methods to multiply decimal numbers.
1. Multiplication of Decimal Number by 10,100 and 1000
- On multiplying a decimal number by 10, the decimal point is shifted to the right by one place.
- On multiplying a decimal number by 100, the decimal point is shifted to the right by two places.
- On multiplying decimal number by 1000, the decimal point is shifted to the right by three places and so on.
i. e. when a decimal number is multiplied by 10,100 or 1000, the digits in the product are same as in the decimal number but the decimal point in the product is shifted to the right by as many of places as there are zeros over one.
2. Multiplication of a Decimal by a Whole Number:
To multiply a decimal number by a whole number.
- First, multiply decimal number by whole number ignoring the decimal point.
- Then, put the decimal point in the product obtained such that there are as many decimal place on the right of the decimal point in the product as in the given decimal number that is multiplied.
3. Multiplication of Two Decimal Numbers To multiply two decimal numbers:
- First, multiply the two decimal numbers without the decimal point (ignoring the decimal points) just like whole numbers.
- Then, In the product, place the decimal point leaving as many digits from the right as the total number of the decimal places in the given decimal numbers.
Division of Decimal Numbers
1. Division of a decimal number by 10,100 and 1000.
- On dividing a decimal number by 10, the decimal point is shifted to the left by one place.
- On dividing a decimal number by 100, the decimal point is shifted to the left by two places.
- On dividing a decimal number by 1000, the decimal point in shifted to the left by three places.
2. Division of a Decimal Number by a Whole Number
To divide a decimal number by a whole number,
- write the given decimal number in fractional form with 10, 100, 1000 or so on as denominator.
- Multiply the fraction so found by the reciprocal of the given whole number (as we do in the division of a fraction by a whole number).
- Finally write the obtained fraction in the decimal form.
3. Division of a Decimal Number by Another Decimal Number
To divide a decimal number by another decimal number,
- Write both the given numbers in fractional form.
- Then follow the method used to divide a fraction by another fraction. In case, the result is a fraction,
- We change it into decimal form.