GSEB Class 8 Maths Notes Chapter 9 બૈજિક પદાવલિઓ અને નિત્યસમ

This GSEB Class 8 Maths Notes Chapter 9 બૈજિક પદાવલિઓ અને નિત્યસમ covers all the important topics and concepts as mentioned in the chapter.

બૈજિક પદાવલિઓ અને નિત્યસમ Class 8 GSEB Notes

→ દરેક પદાવલિ ચલ અને અચલને સાંકળવાથી મળે છે.

→ પદાવલિમાં એકચલ, દ્વિચલ કે તેથી વધારે ચલ હોઈ શકે.

→ જે પદાવલિમાં માત્ર એક જ પદ હોય તે પદાવલિને એકપદી, જે પદાવલિમાં બે પદ હોય તે પદાવલિને દ્વિપદી અને ત્રણ પદ ધરાવતી પદાવલિને ત્રિપદી કહેવાય.

→ એક કે તેથી વધુ પદો કે જેના સહગુણકો શૂન્ય ન હોય તેને બહુપદી કહેવાય

→ જે પદોમાં ચલ સમાન હોય અને સમાન ચલના ઘાતાંક પણ સરખા હોય તેવાં
પદોને સજાતીય પદો કહેવાય. દા. ત., -5x², 7x²; 6xy²z, – 8xy²z

→ જે પદોમાં ચલ અસમાન હોય અથવા સમાન ચલના ઘાતાંક સરખા ન હોય તેવાં પદોને વિજાતીય પદો કહેવાય. દા. ત., 3x, 5y; -4x², – 4x

→ એકપદીને એકપદી સાથે ગુણાકારઃ
બંને એકપદીના સહગુણકોનો ગુણાકાર કરવો. ચલના ઘાતાંકનું ધ્યાન રાખવું
દા. ત., 4ab × 5a²b = 20a³b², -2x²y × 3xy² =- 6x³y³

→ એકપદીનો દ્વિપદી સાથે ગુણાકારઃ
દા. ત., 2x × (5ax -3x) = (2x × 5ax) – (2x × 3x)
= 10ax² – 6x²

→ દ્વિપદીનો દ્વિપદી સાથે ગુણાકારઃ.

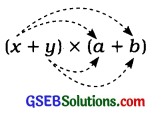
દા. ત., (x + y) × (a + b)
= (x + y) × (a + b)
= x (a + b) + U (a + b)
= ax + bx + ay + by

→ દ્વિપદીનો ત્રિપદી સાથે ગુણાકારઃ દા. ત., (2x + 3g) × (5a + 6b + 7c)
= 2x (5a + 6b + 7c) + 3y(5a + 6b + 7c)
= 10x + 12bx + 14cx + 15ay + 18by + 21cy

→ એવી સમતા કે જેમાં આપેલા ચલની કોઈ પણ કિંમત માટે તે સાચી હોય તો તેને નિત્યસમ (Identity) કહેવાય.