This GSEB Class 9 Maths Notes Chapter 11 રચનાઓ covers all the important topics and concepts as mentioned in the chapter.
રચનાઓ Class 9 GSEB Notes
→ ચોકસાઈવાળી આકૃતિઓ દોરવાની હોય ત્યારે નીચેની સામગ્રીઓ સમાવતી કંપાસપેટી હોવી જરૂરી છે:
- અંક્તિ માપપટ્ટી તેની એક તરફ સેન્ટિમીટર અને મિલિમીટર તથા બીજી તરફ ઇંચ અને તેના ભાગ અંકિત થયેલ હોય છે.
- કાટખૂણિયાની જોડઃ તે પૈકી એકમાં 900, 600 અને 300 ના ખૂણા તથા બીજામાં 900, 450 અને 45 ના ખૂણાનો સમાવેશ થાય છે.
- વિભાજકની જોડઃ જેના બે છેડા કાગળ પર ગોઠવી શકાય તેવી સગવડ સાથે.
- પરિકરની જોડઃ (અથવા પરિકર) જેના એક છેડે પેન્સિલ ગોઠવી શકાય તેવી સગવડ સાથે.
- કોણમાપક
→ માત્ર અન-અંકિત માપપટ્ટી એટલે કે સીધી પટ્ટી અને પરિકર જેવાં બે ઉપકરણોની મદદથી ભૌમિતિક આકૃતિઓ દોરવાની પ્રક્રિયાને ભૌમિતિક રચના કહે છે. જે રચનામાં માપની પણ જરૂર પડે તેમાં અંકિત માપપટ્ટી અને પરિકરનો ઉપયોગ થઈ શકે. જ આ પ્રકરણના પ્રથમ ભાગમાં નીચે મુજબની કેટલીક પાયાની
![]()
→ ભૌમિતિક રચનાઓ કરવાનો અભ્યાસ કરીશું. આ ભૌમિતિક રચનાઓ કરવા માટે માત્ર પરિકર અને માપપટ્ટીનો જ ઉપયોગ કરવાનો છે.
- આપેલા ખૂણાનો દ્વિભાજક (દુભાજક) દોરવાની રચના.
- આપેલા રેખાખંડના લંબદ્વિભાજકની રચના.
- આપેલ કિરણના ઉદ્ભવબિંદુએ 60ના માપના ખૂણાની રચના.
- 15શ્નો ગુણિત હોય, તેવા માપના ખૂણાની રચના.
ઉદાહરણ : 1.
આપેલ કિરણના ઉદ્દભવબિંદુ પર 45ના ખૂણાની રચના કરો અને પ્રમાણિત કરો.
ઉત્તર:
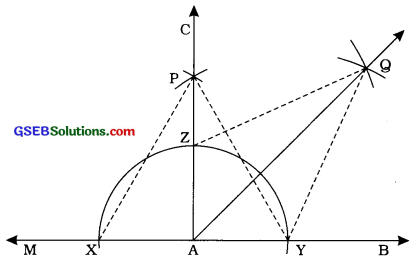
રચનાના મુદ્દા :
- કિરણ AB આપેલ છે. કિરણ ABને A તરફ લંબાવી રેખા MAB મેળવો.
- કોઈ સ્વર ત્રિજ્યા અને કેન્દ્ર A લઈ વર્તુળનું ચાપ દોરો, જે રેખા MABને X અને Xમાં છે.
- \(\frac{1}{2}\)XYથી મોટી ત્રિજ્યા લઈને X અને Yને વારાફરતી કેન્દ્ર લઈ ચાપ દોરો, જે એકબીજાને P બિંદુમાં છેદે.
- Pમાંથી પસાર થાય તેવું કિરણ AC દોરો. આથી આપણને 90નો ∠CAB મળ્યો.
- સૌપ્રથમ દોરેલ A કેન્દ્રિત ચાપ અને કિરણ ACના છેદબિંદુને 2 નામ આપો.
- \(\frac{1}{2}\)YZથી મોટી ત્રિજ્યા લઈને Y અને Zને વારાફરતી કેન્દ્ર લઈ ચાપ દોરો, જે એકબીજાને Q બિંદુમાં છે.
- કિરણ AQ રચો. આમ, ∠QAB માગ્યા મુજબનો 45°નો ખૂણો છે.
રચનાને પ્રમાણિત કરીએઃ
PX અને PX દોરો.
∆PAX અને ∆PAYHI,
AX = AY (એક જ વર્તુળની ત્રિજ્યાઓ)
PX = PY (સમાન વર્તુળની ત્રિજ્યાઓ)
P = PA (સામાન્ય રેખાખંડ)
બાબાબા મુજબ, ∆PAX ≅ ∆PAY.
∠PAX = ∠PAY (CPCT).
પરંતુ, ∠PAX + ∠PAY = 180° (રખિક જોડ)
∴ ∠PAY = \(\frac{180°}{2}\) = 90°
∠CAB = 90°
રેખાખંડ 07 અને QX દોરી, ∆AZQ અને ∆AYQ મેળવો.
∆AYQ અને ∆ZQHI,
AY = AZ (એક જ વર્તુળની ત્રિજ્યાઓ)
YQ = ZQ (સમાન વર્તુળની ત્રિજ્યાઓ)
AQ = AQ (સામાન્ય રેખાખંડ)
બાબાબા મુજબ, ∆AYQ = ∆AZQ
∴ ∠QAY = ∠QAZ (CPCT)
પરંતુ, ∠QAY + ∠QAZ = ∠ZAY = ∠CAB = 90°,
∴ ∠AY = \(\frac{90°}{2}\) = 45°
∴ ∠QAB = 45°
ઉદાહરણ : 2.
નીચે આપેલા માપના ખૂણાઓની રચના કરોઃ
(1) 30°
ઉત્તર:
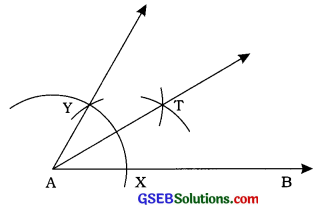
રચનાના મુદ્દા :
- કોઈ પણ કિરણ AB દોરો. કોઈ સ્વૈર ત્રિજ્યા લઈ અને કેન્દ્ર A લઈ વર્તુળનું ચાપ દોરો, જે કિરણ ABને આમાં છેદે.
- તે જ ત્રિજ્યા અને X કેન્દ્ર લઈ વર્તુળનું ચાપ દોરો, જે પ્રથમ ચાપને Y બિંદુમાં છેદે. કિરણ AY દોરો, જેથી ∠YAB = 600 થાય.
- ∠YABનો દ્વિભાજક AT દોરો. આમ, ∠TAB એ 30°નો માગ્યા મુજબનો ખૂણો છે.
(2) 22\(\frac{1}{2}\)°
ઉત્તર:
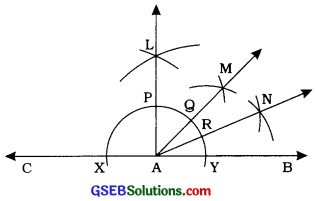
રચનાના મુદ્દા:
- કોઈ પણ કિરણ AB દોરો. તેને A તરફ લંબાવી રેખા CAB મેળવો.
- A કેન્દ્ર અને કોઈ સ્વર ત્રિજ્યા લઈ વર્તુળનું ચાપ દોરો, જે રેખા CABને X અને Yમાં છેદે.
- \(\frac{1}{2}\)XYથી મોટી ત્રિજ્યા લઈ અને વારાફરતી X અને Y કેન્દ્ર લઈ વર્તુળના ચાપ દોરો, જે L બિંદુમાં છે. આમ, ∠LAB = 900 મળે.
- ∠LABનો દ્વિભાજક AM રચો, જેથી ∠MAB = 45 મળે.
- ∠MABનો દ્વિભાજક AN રચો, જેથી ∠NAB = 22\(\frac{1}{2}\)° મળે. આમ, ∠NAB એ 22\(\frac{1}{2}\)°નો માગ્યા મુજબનો ખૂણો છે.
→ ત્રિકોણની કેટલીક રચનાઓ ત્રિકોણની એકરૂપતાની શરતોને અનુસરતા જો
- બે બાજુ અને અંતર્ગત ખૂણો આપેલ હોય,
- ત્રણ બાજુઓ આપેલ હોય,
- બે ખૂણા અને અંતર્ગત બાજુ (અથવા કોઈ પણ બાજુ) આપેલ હોય,
- કાટકોણ ત્રિકોણમાં કર્ણ તથા એક બાજુ આપેલ હોય, તો અનન્ય ત્રિકોણ મળે.
→ હવે, ત્રિકોણની નીચે દર્શાવ્યા મુજબની કેટલીક વધુ રચનાઓનો અભ્યાસ કરીએ:
- જ્યારે ત્રિકોણનો પાયો, પાયા પરનો એક ખૂણો અને બાકીની બે બાજુઓના માપનો સરવાળો આપ્યો હોય, તેવા ત્રિકોણની રચના.
- જ્યારે ત્રિકોણનો પાયો, પાયા પરનો એક ખૂણો અને બાકીની બે બાજુઓના માપનો તફાવત આપ્યો હોય, તેવા ત્રિકોણની રચના.
- ત્રિકોણના પાયાના બે ખૂણા અને ત્રિકોણની પરિમિતિ આપી હોય, તેવા ત્રિકોણની રચના.
![]()
ઉદાહરણ : 1.
BC = 8 સેમી, ∠B = 75૦ અને AB + AC = 15 સેમી હોય તેવા ત્રિકોણ ABCની રચના કરો.
ઉત્તર:
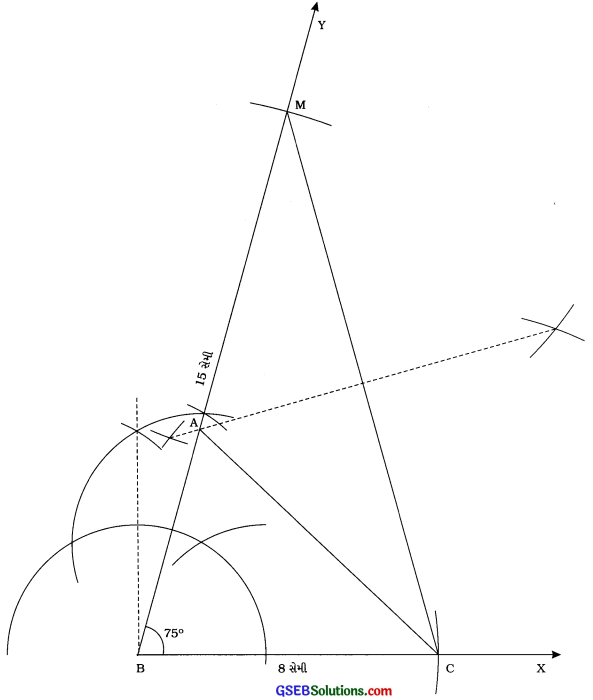
રચનાના મુદ્દા:
- કિરણ BX દોરો. B કેન્દ્રિત 8 સેમી ત્રિજ્યાવાળો ચાપ દોરો, જે BXને તેમાં છે.
- બિંદુ B આગળ ∠YBC રચો, જેનું માપ 75° થાય.
- B કેન્દ્રિત 15 સેમી ત્રિજ્યાવાળો ચાપ દોરો, જે કિરણ BYને Mમાં છેદે.
- MC દોરો અને તેનો લંબદ્વિભાજક રચો, જે BMને તેમાં છે.
- AC દોરો. આમ, A ABC એ આપેલ માપવાળો ત્રિકોણ છે.
ઉદાહરણ : 2.
QR = 9 સેમી, ∠Q = 60° અને PR – PQ = 3 સેમી હોય તેવા ત્રિકોણ PQRની રચના કરો.
ઉત્તર:
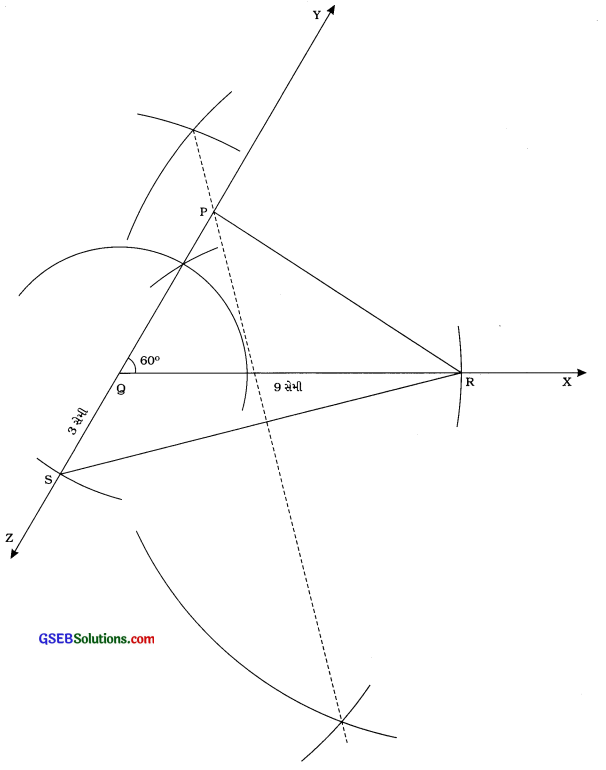
રચનાના મુદ્દા:
- કિરણ 9x દોરીને 9 સેમી લંબાઈનો રેખાખંડ OR મેળવો.
- બિંદુ છુ આગળ કિરણ QYની રચના કરો, જેથી ∠YQR = 600 થાય.
- કિરણ QYને Q તરફ લંબાવી કિરણ 32 દોરો અને તેની પર QS = 3 સેમી થાય તેવું બિંદુ = મેળવો.
- રેખાખંડ RS દોરી તેનો લંબદ્વિભાજક રચો, જે કિરણ QY Pમાં છે.
- રેખાખંડ PR દોરો. આમ, ∆POR એ આપેલ માપવાળો ત્રિકોણ છે.
ઉદાહરણ : 3.
∠Y = 30, 27 = 90° અને આ XY + YZ + ZX = 8 સેમી હોય તેવા ત્રિકોણ XYZની રચના કરો.
ઉત્તર:
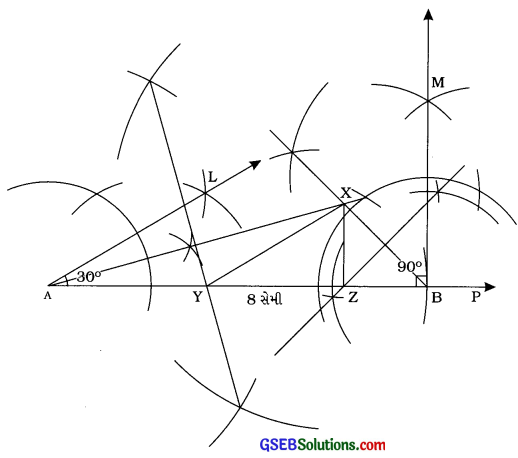
રચનાના મુદ્દા:
- કિરણ AP દોરીને 8 સેમી લંબાઈનો રેખાખંડ AB મેળવો.
- કિરણ AL એવું રચો, જેથી ∠LAB = 300 થાય.
- કિરણ BM એવું રચો, જેથી ∠MBA = 90° થાય.
- ∠LAB અને ∠MBAના દ્વિભાજકો દોરો અને તેમનાં છેદબિંદુને X નામ આપો.
- રેખાખંડ XB દોરો તથા તેનો લંબદ્વિભાજક રચો, જે ABને Zમાં છેદે.
- રેખાખંડ XA દોરો તથા તેનો લંબદ્વિભાજક રચો, જે ABને જમાં છે.
- રેખાખંડ XY તથા XZ દોરો. આમ, ∆XYZ એ આપેલ માપવાળો ત્રિકોણ છે.
![]()
ઉદાહરણ : 4.
પાયો 6 સેમી અને કર્ણ તથા બીજી બાજુનો સરવાળો 9 સેમી 3 હોય તેવા કાટકોણ ત્રિકોણની રચના કરો.
ઉત્તર:
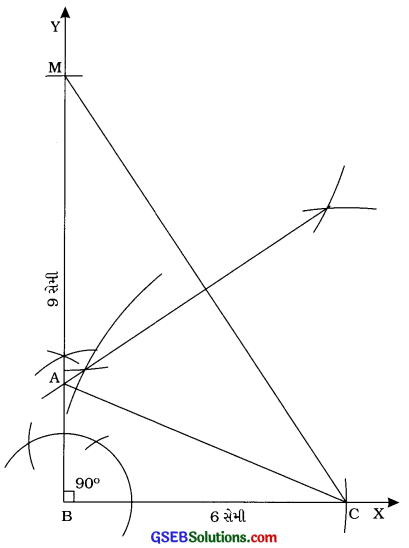
રચનાના મુદ્દા:
- કિરણ BX દોરીને 6 સેમી લંબાઈનો રેખાખંડ BC મેળવો.
- કિરણ BY એવું રચો, જેથી ∠YBC = 90° થાય.
- B કેન્દ્ર અને 9 સેમી ત્રિજ્યાવાળો ચાપ દોરો, જે કિરણ BYને M બિંદુમાં છેદે.
- રેખાખંડ CM દોરી તેનો લંબદ્વિભાજક રચો, જે BMને A બિંદુમાં છેદે.
- રેખાખંડ AC રચો. આમ, A ABC એ આપેલ માપવાળો કાટકોણ ત્રિકોણ છે. જેમાં ∠B કાટખૂણો છે, BC = 6 સેમી છે તથા AB + AC = 9 સેમી છે.