This GSEB Class 9 Maths Notes Chapter 12 હેરોનું સૂત્ર covers all the important topics and concepts as mentioned in the chapter.
હેરોનું સૂત્ર Class 9 GSEB Notes
→ ત્રિકોણનું ક્ષેત્રફળઃ ત્રિકોણનું ક્ષેત્રફળ શોધવા માટે વપરાતા નીચેનાં સૂત્રથી આપણે પરિચિત છીએ
ત્રિકોણનું ક્ષેત્રફળ = \(\frac{1}{2}\) × પાયો × વેધ
ચોક્કસ પ્રકારના ત્રિકોણ માટે આ જ સૂત્ર બીજા સ્વરૂપે રજૂ થઈ શકે છે, જેમ કે કાટકોણ ત્રિકોણના ક્ષેત્રફળ માટે નીચે મુજબ સૂત્ર લઈ શકાય
→ કાટકોણ ત્રિકોણનું ક્ષેત્રફળ = \(\frac{\sqrt{3}}{4}\) × કાટખૂણો બનાવતી બે બાજુઓનો ગુણાકાર
સમબાજુ ત્રિકોણ માટે પાયથાગોરસના પ્રમેયના ઉપયોગ દ્વારા વેધ શોધીએ, તો સૂત્ર નીચે મુજબના સ્વરૂપમાં ફેરવાય : સમબાજુ ત્રિકોણનું ક્ષેત્રફળ = 2 × (બાજુ)
સમદ્વિભુજ ત્રિકોણમાં પણ જો ત્રણ બાજુના માપ જાણતા હોઈએ, તો પાયથાગોરસના પ્રમેય પરથી વેધનું માપ જાણી શકાય અને મૂળ સૂત્રનો ઉપયોગ થઈ શકે. પરંતુ, વિષમબાજુ ત્રિકોણની ત્રણેય બાજુના માપ જાણતા હોઈએ તોપણ વેધનું માપ શોધી ન શકીએ.
→ હેરોનનું સૂત્રઃ કોઈ પણ પ્રકારના કોઈ પણ ત્રિકોણની ત્રણેય બાજુઓનાં માપ જાણતા હોઈએ, તો તે પરથી ત્રિકોણનું ક્ષેત્રફળ શોધવાનું સૂત્ર હેરોન નામના ગણિતશાસ્ત્રીએ આપ્યું છે. હેરોનનું સૂત્ર નીચે મુજબ છે:
ત્રિકોણનું ક્ષેત્રફળ = \(\sqrt{s(s-a)(s-b)(s-c)}\)
જ્યાં, a, b અને C ત્રિકોણની ત્રણ બાજુઓનાં માપ દર્શાવે છે અને s = \(\frac{a+b+c}{2}\) : એ ત્રિકોણની અર્ધપરિમિતિ છે.
![]()
→ ક્ષેત્રફળના એકમ કોઈ સમતલ આકૃતિના ક્ષેત્રફળનો એકમ ચોરસ મીટર (મી2) અથવા ચોરસ સેન્ટિમીટર (સેમી2) વગેરે લખાય. જમીનના નાના-મોટા પ્લૉટનું ક્ષેત્રફળ હેક્ટરમાં લખાય છે.
1 હેક્ટર = 10,000 મી2
ઉદાહરણ : 1.
એક ત્રિકોણની બાજુઓનાં માપ 12 સેમી, 17 સેમી અને 25 સેમી છે, તો તે ત્રિકોણનું ક્ષેત્રફળ શોધો.
ઉત્તર:
અહીં, આપેલ ત્રિકોણ માટે a = 12 સેમી, b = 17 સેમી અને c = 25 સેમી છે.
અર્ધપરિમિતિ s = \(\frac{a+b+c}{2}\)
= \(\frac{12+17+25}{2}=\frac{54}{2}\) = 27 સેમી
આથી s- a = 27 – 12 = 15 સેમી,
s – b = 27 – 17 = 10 સેમી અને
s – c = 27 – 25 = 2 સેમી.
ત્રિકોણનું ક્ષેત્રફળ = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{27 \times 15 \times 10 \times 2}\) સેમી2
= \(\sqrt{9 \times 3 \times 3 \times 5 \times 5 \times 2 \times 2}\) સેમી2
= 3 × 3 × 5 × 2 સેમી2
= 90 સેમી2
ઉદાહરણ : 2.
એક ત્રિકોણાકાર ખેતરની બાજુઓનાં માપ 5 મી, 12 મી અને 53 મી છે, તો તે ખેતરનું ક્ષેત્રફળ શોધો.
ઉત્તર:
આપેલ ત્રિકોણાકાર ખેતર માટે a = 51 મી, b = 52 મી અને c = 53 મી છે.
અર્ધપરિમિતિ s = \(\frac{a+b+c}{2}\)
= \(\frac{51+52+53}{2}=\frac{156}{2}\) = 78મી
આથી s – a = 78 – 51 = 27 મી,
s – b = 78 – 52 = 26 મી અને
s – c = 78 – 53 = 25 મી.
ત્રિકોણાકાર ખેતરનું ક્ષેત્રફળ = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{78 \times 27 \times 26 \times 25}\) મી2
= \(\sqrt{13 \times 2 \times 3 \times 3 \times 9 \times 13 \times 2 \times 5 \times 5}\) મી2
= 13 × 2 × 3 × 3 × 5 મી2
= 1170 મી2
ઉદાહરણ : 3.
એક ત્રિકોણાકાર પ્લૉટની બાજુઓની લંબાઈ 4: 7:9ના પ્રમાણમાં છે. જો તે પ્લૉટની પરિમિતિ 500 મી હોય, તો તેનું ક્ષેત્રફળ શોધો.
ઉત્તર:
ધારો કે, આપેલ ત્રિકોણાકાર પ્લૉટની બાજુઓની લંબાઈ 4xમી, 7xમી અને 9x મી છે.
પ્લૉટની પરિમિતિ 500 મી આપેલ છે.
∴ 4x + 7x + 9x = 500
∴ 20x = 500
∴ x = 25
આથી આપેલ ત્રિકોણાકાર પ્લૉટ માટે,
a = 4 × 25 = 100 મી,
b = 7 × 25 = 175 મી અને
c = 9 × 25 = 225 મી.
![]()
હવે, s – a = 250 – 100 = 150 મી,
s – b = 250 – 175 = 75 મી અને
s – c = 250 – 225 = 25 મી.
ત્રિકોણાકાર પ્લૉટનું ક્ષેત્રફળ = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{250 \times 150 \times 75 \times 25}\) મી2
= \(\sqrt{25 \times 10 \times 10 \times 5 \times 3 \times 3 \times 25 \times 25}\) મી2
= 5 × 10 × 3 × 25√5 મી2
= 3750 √5 મી2
→ ચતુષ્કોણનાં ક્ષેત્રફળ શોધવા હેરોનના સૂત્રનો ઉપયોગ : જે ચતુષ્કોણની બાજુઓ અને એક વિકર્ણનાં માપ આપેલ હોય તે ચતુષ્કોણનું ક્ષેત્રફળ શોધવા તેને બે ત્રિકોણોમાં વિભાજિત કરીને હેરોનના સૂત્રનો ઉપયોગ કરવામાં આવે છે.
→ ચતુષ્કોણ ABCDમાં વિકર્ણ AC પર B અને Dમાંથી દોરેલ વેધની લંબાઈ અનુક્રમે h1 અને h2 હોય, તો
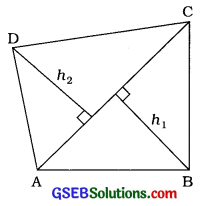
ચતુષ્કોણ ABCDનું ક્ષેત્રફળ = ∆ABCનું ક્ષેત્રફળ + ∆ACDનું ક્ષેત્રફળ
= (\(\frac{1}{2}\) × AC × h1 ) + (\(\frac{1}{2}\) × AC × h2) = \(\frac{1}{2}\) × AC × (h1 + h2) એક
→ ચોક્કસ પ્રકારના ચતુષ્કોણોના ક્ષેત્રફળ માટેનાં સૂત્રો મળે જ છે. જેમ કે, ચોરસનું ક્ષેત્રફળ
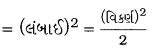
લંબચોરસનું ક્ષેત્રફળ = લંબાઈ × પહોળાઈ
સમાંતરબાજુ ચતુષ્કોણનું ક્ષેત્રફળ = પાયો × પાયાને અનુરૂપ વેધ
સમબાજુ ચતુષ્કોણનું ક્ષેત્રફળ = \(\frac{1}{2}\) × બે વિકર્ણોનો ગુણાકાર
સમલંબ ચતુષ્કોણનું ક્ષેત્રફળ = \(\frac{1}{2}\) × સમાંતરબાજુઓનો સરવાળો × સમાંતરબાજુઓ વચ્ચેનું અંતર
![]()
ઉદાહરણ : 1.
ચતુષ્કોણ ABCDમાં AB = 40 સેમી, BC = 35 સેમી, CD = 48 સેમી, DA = 29 સેમી અને BD = 29 સેમી હોય, તો ચતુષ્કોણ ABCDનું ક્ષેત્રફળ શોધો.
ઉત્તર:
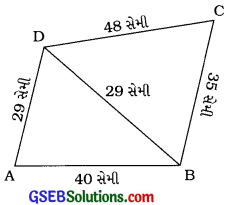
B વિકર્ણ BD દ્વારા ચતુષ્કોણ ABCD પરસ્પર આચ્છાદિત ન થતા હોય તેવા બે ત્રિકોણો ∆ABP અને ∆BCDમાં વિભાજિત થાય છે.
∆ABD માટે a = 40 સેમી, b = 29 સેમી અને c = 29 સેમી.
અર્ધપરિમિતિ s = \(\frac{a+b+c}{2}\)
= \(\frac{40+29+29}{2}=\frac{98}{2}\) = 49 સેમી
∆ABDનું ક્ષેત્રફળ = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{49(49-40)(49-29)(49-29)}\) સેમી2
= \(\sqrt{49 \times 9 \times 20 \times 20}\) સેમી2
= 7 × 3× 20 સેમી2
= 420 સેમી2
∆BCD માટે a = 29 સેમી, b = 48 સેમી અને c = 35 સેમી.
અર્ધપરિમિતિ s = \(\frac{a+b+c}{2}\)
\(\frac{29+48+35}{2}=\frac{112}{2}\) = 56 સેમી
∆BCDનું ક્ષેત્રફળ = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{56(56-29)(56-48)(56-35)}\) સેમી2
= \(\sqrt{56 \times 27 \times 8 \times 21}\) સેમી2
= \(\sqrt{8 \times 7 \times 9 \times 3 \times 8 \times 7 \times 3}\) સેમી2
= 8 × 7 × 3 × 3 સેમી2
= 504 સેમી2
હવે, ચતુષ્કોણ ABCDનું ક્ષેત્રફળ
= ∆ABDનું ક્ષેત્રફળ + ∆BCDનું ક્ષેત્રફળ
= 420 + 504 સેમી2
= 924 સેમી2
ઉદાહરણ : 2.
ચતુષ્કોણ ABCDમાં ∠A = 90°, AB = 15 સેમી, BC = 25 સેમી, CD = 12 સેમી અને DA = 8 સેમી હોય, તો ચતુષ્કોણ ABCDનું ક્ષેત્રફળ શોધો.
ઉત્તર:
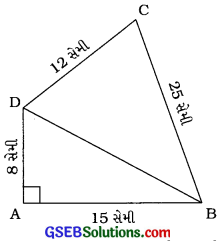
∆ABDમાં ∠A = 90°, AB = 15 સેમી અને AD = 8 સેમી.
BD = \(\sqrt{\mathrm{AB}^{2}+\mathrm{AD}^{2}}\)
= \(\sqrt{15^{2}+8^{2}}\) સેમી
= \(\sqrt{225+64}\) સેમી
= \(\sqrt{289}\) સેમી
= 17 સેમી
કાટકોણ ∆ABDનું ક્ષેત્રફળ = \(\frac{1}{2}\)AB × AD
= \(\frac{1}{2}\) × 15 × 8 સેમી2
= 60 સેમી2
∆BCDમાં વ = 17 સેમી, b = 25 સેમી અને c = 12 સેમી.
અર્ધપરિમિતિ s = \(\frac{a+b+c}{2}\)
= \(\frac{17+25+12}{2}\)
= \(\frac{54}{2}\)
= 27 સેમી
∴ s – a = 27 – 17 = 10 સેમી,
s – b = 27 – 25 = 2 સેમી અને
s – c = 27 – 12 = 15 સેમી.
∆BCDનું ક્ષેત્રફળ = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{27 \times 10 \times 2 \times 15}\) સેમી2
= \(\sqrt{9 \times 3 \times 5 \times 2 \times 2 \times 5 \times 3}\) સેમી2
= 3 × 3 × 5 × 2 સેમી2
= 90 સેમી2
ચતુષ્કોણ ABCDનું ક્ષેત્રફળ
= ∆ABDનું ક્ષેત્રફળ + ∆BCDનું ક્ષેત્રફળ
= 60 + 90 સેમી2
= 150 સેમી2
![]()
ઉદાહરણ : 3.
સમબાજુ ચતુષ્કોણ આકારના એક પ્લૉટની પરિમિતિ 340 મી અને એક વિકર્ણની લંબાઈ 72 મી છે. આ પ્લૉટનું ક્ષેત્રફળ 3 શોધો.
ઉત્તર:
ધારો કે, ABCD સમબાજુ ચતુષ્કોણ આકારનો પ્લૉટ છે. વિકર્ણ BD દ્વારા તેનું બે એકરૂપ ત્રિકોણોમાં એટલે કે સમક્ષેત્ર ત્રિકોણોમાં વિભાજન થાય છે.
∆ABDનું ક્ષેત્રફળ = ∆BCDનું ક્ષેત્રફળ
આથી સમબાજુ ચતુષ્કોણ ABCDનું ક્ષેત્રફળ
= 2 × ∆ABDનું ક્ષેત્રફળ
સમબાજુ ચતુષ્કોણ ABCDની પરિમિતિ = 340 મી
દરેક બાજુની લંબાઈ = \(\frac{340}{4}\) = 85 મી આથી
∆ABDમાં AB = AD = 85 મી અને BD = 72 મી.
∆ABDમાં a = 85 મી, b = 85 મી અને c = 72 મી.
અર્ધપરિમિતિ s = \(\frac{a+b+c}{2}\)
= \(\frac{85+85+72}{2}\)
= \(\frac{242}{2}\)
= 121 મી
આથી s – a = 121 – 85 = 36 મી,
s- b = 121 – 85 = 36 મી અને
s – c = 121 – 72 = 49 મી.
∆ABDનું ક્ષેત્રફળ = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{121 \times 36 \times 36 \times 49}\) મી2
= 11 × 36 × 7 મી2
= 2772 મી2
સમબાજુ ચતુષ્કોણ ABCDનું ક્ષેત્રફળ
= 2 × ∆ABDનું ક્ષેત્રફળ
= 2 × 2772 મી2
= 5544 મી2
આમ,આપેલ સમબાજુ ચતુષ્કોણ આકારના પ્લોટનું ક્ષેત્રફળ 5544 મી2 છે.