GSEB Class 9 Maths Notes Chapter 14 આંકડાશાસ્ત્ર

This GSEB Class 9 Maths Notes Chapter 14 આંકડાશાસ્ત્ર covers all the important topics and concepts as mentioned in the chapter.

આંકડાશાસ્ત્ર Class 9 GSEB Notes

→ માહિતી Data) : જે આંકડાકીય સત્યો કે બિનઆંકડાકીય (ગુણધર્મ આધારિત) સત્યો ચોક્કસ હેતુસર એકત્રિત કરવામાં ‘ આવે છે, તે હકીકતો અને આંકડાઓને માહિતી કહે છે.

→ આંકડાશાસ્ત્ર (Statistics) : માહિતીનું અર્થપૂર્ણ તારણ કાઢવાની ગણિતની શાખાને આંકડાશાસ્ત્ર કહે છે. આમ, આંકડાશાસ્ત્ર એ માહિતી એકત્રિત કરવી, તેને વ્યવસ્થિત ગોઠવવી, તેનું વિશ્લેષણ કરવું અને અર્થપૂર્ણ તારણ મેળવવા સાથે સંકળાયેલ એક વિષય છે.

→ માહિતીનું એકત્રીકરણ :

• પ્રાથમિક માહિતી (Primary data): જ્યારે તપાસકર્તાએ કોઈ ચોક્કસ હેતુ ધ્યાનમાં રાખીને તેણે જાતે માહિતી મેળવી હોય તેવી માહિતીને પ્રાથમિક માહિતી કહે છે.
• ગૌણ માહિતી (Secondary data): જો તપાસકર્તાએ પહેલાંથી એકત્રિત થયેલી માહિતીના સ્ત્રોતમાંથી માહિતી મેળવી હોય, તો આવી માહિતીને ગૌણ માહિતી કહે છે.

→ માહિતીની રજૂઆતઃ જ્યારે તપાસકર્તા માહિતી એકત્રિત કરે ત્યારે તે જે સ્વરૂપમાં હોય છે, તેને કાચી માહિતી (Raw data) કહે છે. આવી માહિતીને એવા સ્વરૂપમાં રજૂ કરવી જોઈએ કે જેથી તે અર્થપૂર્ણ હોય, સરળતાથી સમજી શકાય અને પહેલી નજરે તેના મુખ્ય ઉદ્દેશો જાણી શકાય.
માહિતીમાં સમાવિષ્ટ થતી હકીકતને રજૂ કરતાં આંકડાઓને અવલોકન કહે છે. અવલોકનો જુદા જુદા મૂલ્ય ધારણ કરતા હોવાથી તેને ચલ કહે છે. આમ, ચલનાં જુદાં જુદાં મૂલ્યોને અવલોકન કહે છે.

→ વિસ્તાર માહિતીનાં મહત્તમ અને ન્યૂનતમ મૂલ્યોના તફાવતને માહિતીનો વિસ્તાર (Range) કહે છે.

→ માહિતીનું વર્ગીકરણ: અવર્ગીક્ત આવૃત્તિ-વિતરણ કોષ્ટક (Ungrouped frequency distribution table) : માહિતીમાં ચલની કોઈ નિશ્ચિત કિંમત જો n વખત આવતી હોય, તો તે કિંમતની આવૃત્તિ 1 કહેવાય છે. ચલની જુદી જુદી કિંમતોની સામે તે કિંમતની આવૃત્તિ કોષ્ટકમાં રજૂ કરીએ તેવા કોષ્ટકને અવર્ગીકૃત આવૃત્તિ-વિતરણ કોષ્ટક કહે છે.

→ વર્ગ (Class) અથવા વર્ગ-અંતરાલ (Class-interval): મોટી સંખ્યાની માહિતી રજૂ કરવા માટે વાચક સરળતાથી સમજી શકે તે માટે જૂથોમાં ગોઠવવામાં આવે છે. આ જૂથોને વર્ગો અથવા વર્ગ-અંતરાલ કહેવાય છે. દરેક વર્ગની લંબાઈને, એટલે કે ઊર્ધ્વસીમા અને અધઃસીમાના તફાવતને, વર્ગલંબાઈ (Class size) અથવા પહોળાઈ (Class width) કહે છે, દરેક વર્ગની નાનામાં નાની સંખ્યાને તે વર્ગની અધવર્ગસીમા (Lower class limit) અને મોટામાં મોટી સંખ્યાને ઊર્ધવર્ગસીમા (Upper class limit) કહે છે. દરેક વર્ગની સામે તેની આવૃત્તિ રજૂ કરતા કોષ્ટકને વર્ગીકૃત આવૃત્તિવિતરણ કોષ્ટક (Grouped frequency distribution table) કહે છે.

વર્ગીકૃત આવૃત્તિ-વિતરણ કોષ્ટકના વર્ગો બે પ્રકારના હોય છે:
(1) પરસ્પર અનાચ્છાદિત વર્ગો: જ્યારે વર્ગો એ પ્રકારના હોય કે કોઈ પણ વર્ગની અધ:વર્ગસમા તેનાથી આગળના વર્ગની ઊર્ધ્વવર્ગસીમાથી ભિન્ન હોય ત્યારે તેવા વર્ગોને પરસ્પર અનાચ્છાદિત વર્ગો કહે છે. દા. ત., વગ 1 – 10, 11 – 20, 21 – 30, … વગેરે.

(2) સતત વર્ગો: જ્યારે વગોં એ પ્રકારના હોય કે કોઈ પણ વર્ગની અધવર્ગસીમા એ તેનાથી આગળના વર્ગની ઊર્ધ્વવર્ગસીમાને સમાન હોય ત્યારે તેવા વર્ગોને સતત વર્ગો કહે છે. દા. ત., વર્ગો 0 – 5, 5 – 10, 10 – 15, 15-20, . વગેરે. સતત વર્ગો માટે નિયમ છે કે તેમાં વર્ગની ઊર્ધ્વવર્મસીમાનો સમાવેશ થતો નથી. એટલે કે વર્ગો 0 – 5, 5 – 10, 10 – 15, … હોય, તો અવલોકન 5નો સમાવેશ વર્ગ 0- 5માં નહીં થાય, પરંતુ વર્ગ 5 – 10માં થશે. તે જ રીતે અવલોકન 10નો સમાવેશ વર્ગ 5 – 10માં | નહીં, પરંતુ વર્ગ 10 – 15માં થશે. પરસ્પર અનાચ્છાદિત વર્ગોને સતત વર્ગોમાં ફેરવવા માટે કોઈ પણ વર્ગની ઊર્ધ્વસીમા અને તે પછીના વર્ગની અધઃસીમા વચ્ચેનું અંતર શોધીને તે અંતરનો અડધો ભાગ દરેક વર્ગની ઊર્ધ્વસીમામાં ઉમેરવામાં આવે અને અધઃસીમામાંથી બાદ કરવામાં આવે છે.

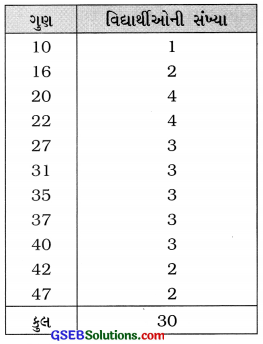
ઉદાહરણ : 1.
30 વિદ્યાર્થીઓ ગણિતની 50 ગુણની કસોટીમાં મેળવેલ ગુણ નીચે મુજબ છે :

આપેલ માહિતીને અવર્ગીકૃત આવૃત્તિ-વિતરણ કોષ્ટકમાં રજૂ કરો.
ઉત્તર:

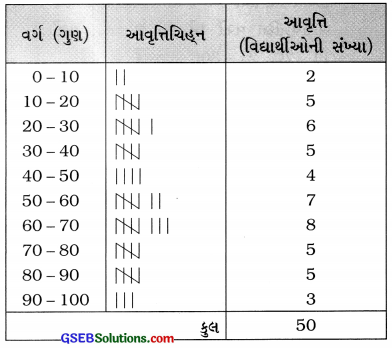
ઉદાહરણ : 2.
50 વિદ્યાર્થીઓએ ગણિતની 100 ગુણની પરીક્ષામાં મેળવેલ ગુણની માહિતી નીચે મુજબ છે :

આપેલ માહિતી પરથી 0 – 10, 10 – 20,. વર્ગો હોય તેવું આવૃત્તિ-વિતરણ તૈયાર કરો.
ઉત્તર:

→ માહિતીની આલેખાત્મક રજૂઆત (Graphical representation of data) : માહિતીની ચિત્રાત્મક રજૂઆતને આલેખાત્મક રજૂઆત કહે છે.
આપણે ત્રણ પ્રકારની ચિત્રાત્મક રજૂઆત અંગે અભ્યાસ કરીશું:

• લંબાલેખ (Bar graphy)
• સમાન પહોળાઈ અને અસમાન પહોળાઈના ખંભાલેખ (Histograms of uniform width and of varying width)
• આવૃત્તિ બહુકોણ (Frequency polygon)

→ લંબાલેખઃ જેમાં સામાન્ય રીતે સમાન પહોળાઈવાળા લંબચોરસ કે જે જુદા જુદા ચલો દર્શાવી, તેને એક અક્ષ પર (ધારો કે x-અક્ષ) સમાન અંતરે દોરવામાં આવે છે, એવી માહિતીની ચિત્રાત્મક રજૂઆત એ લંબાલેખ છે. બીજા અક્ષ (ધારો કે, પુ-અક્ષ) પર ચલનું મૂલ્ય દર્શાવવામાં આવે છે. લંબચોરસની ઊંચાઈ તેના ચલની કિંમત પર આધારિત છે.

→ ખંભાલેખઃ આ આલેખ એ લંબાલેખની આલેખાત્મક રજૂઆતનું જ સ્વરૂપ છે, પરંતુ તે સતત વર્ગો માટે વપરાય છે. ખંભાલેખ બે પ્રકારના હોય છે

1. સમાન પહોળાઈના ખંભાલેખ અને
2. અસમાન પહોળાઈના ખંભાલેખ.

(1) સમાન પહોળાઈના ખંભાલેખઃ ખંભાલેખ દોરવા માટે ૪-અક્ષ પર સમાન વર્ગલંબાઈવાળા વર્ગનાં વર્ગસીમાબિંદુઓને અને ઇ-અક્ષ પર આવૃત્તિઓને યોગ્ય પ્રમાણમાપ વડે દર્શાવવામાં આવે છે. આ સ્તંભાલેખ માટે દરેક વર્ગ ઉપર તે વર્ગની આવૃત્તિના પ્રમાણમાં ઊંચાઈ ધરાવતો સ્તંભ દોરવામાં આવે છે. સ્તંભની સંખ્યા વર્ગની સંખ્યા જેટલી હોય છે. આ રીતે મળતી આકૃતિને સમાન પહોળાઈનો ખંભાલેખ કહે છે. આ સ્તંભાલેખનો દરેક સ્તંભ લંબચોરસ છે, જેનો પાયો વર્ગલંબાઈ છે અને ઊંચાઈ તેને અનુરૂપ આવૃત્તિ જેટલી હોય છે.

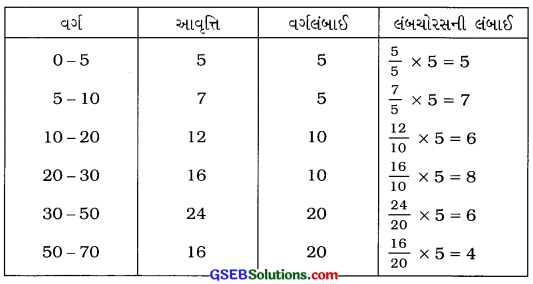
(2) અસમાને પહોળાઈના ખંભાલેખઃ અસમાન વર્ગ લંબાઈવાળા આવૃત્તિ-વિતરણનો ખંભાલેખ દોરવા લંબચોરસની લંબાઈને પ્રમાણસર બનાવવી પડે. લંબચોરસની ઊંચાઈ (સપ્રમાણ આવૃત્તિ) માટે નીચેનું સૂત્ર ઉપયોગમાં લેવાય છે:

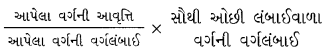
આ પ્રકારના ખંભાલેખમાં લંબચોરસની પહોળાઈ જુદી જુદી હોય છે અને લંબચોરસનું ક્ષેત્રફળ આવૃત્તિના સપ્રમાણમાં હોય છે.

→ આવૃત્તિ-બહુકોણ (Frequency polygon) આવૃત્તિવિતરણના દરેક વર્ગની મધ્યકિંમતને ૮-અક્ષ પર દર્શાવવામાં આવે છે અને જે-તે મધ્યકિંમતવાળા વર્ગની આવૃત્તિને ઇ-અક્ષ પર દર્શાવવામાં આવે છે.

પ્રથમ વર્ગની પહેલાંના સંભવિત વર્ગની મધ્યકિંમત અને અંતિમ વર્ગની પછીના સંભવિત વર્ગની મધ્યકિંમત પણ આલેખ પર દર્શાવવામાં આવે છે અને તે બંનેને સંગત આવૃત્તિ શૂન્ય (0) લેવામાં આવે છે. આ વર્ગોની મધ્યકિંમતો દર્શાવતા બિંદુઓને પણ આલેખમાં દર્શાવવામાં આવે છે. આમ, દર્શાવવાની મધ્યકિંમતોની સંખ્યા આપેલા વર્ગોની સંખ્યા કરતાં 2 વધારે હોય છે.

મેળવેલાં બિંદુઓને ક્રમમાં રેખાખંડો વડે જોડવામાં આવે છે. આ રીતે મળેલા આલેખને આવૃત્તિ-બહુકોણ કહે છે. આવૃત્તિબહુકોણ x-અક્ષ સાથે બંધ આકૃતિ રચે છે.

આપેલ સતત આવૃત્તિ-વિતરણનો સ્તંભાલેખ દોરેલ હોય, તો લંબચોરસના ઉપરની બાજુનાં મધ્યબિંદુઓને (x-અક્ષ પર લીધેલા સંભવિત વર્ગોનાં મધ્યબિંદુઓ સહિત) ક્રમશઃ રેખાખંડો વડે જોડવાથી આપેલ સતત આવૃત્તિ-વિતરણનો આવૃત્તિ-બહુકોણ મળે છે.

જો પ્રથમ વર્ગ 0થી શરૂ થતો ન હોય, તો પ્રમાણમાપ બંધબેસતું કરવા x-અક્ષ પર કાપ કે છેદ મૂકવામાં આવે છે.

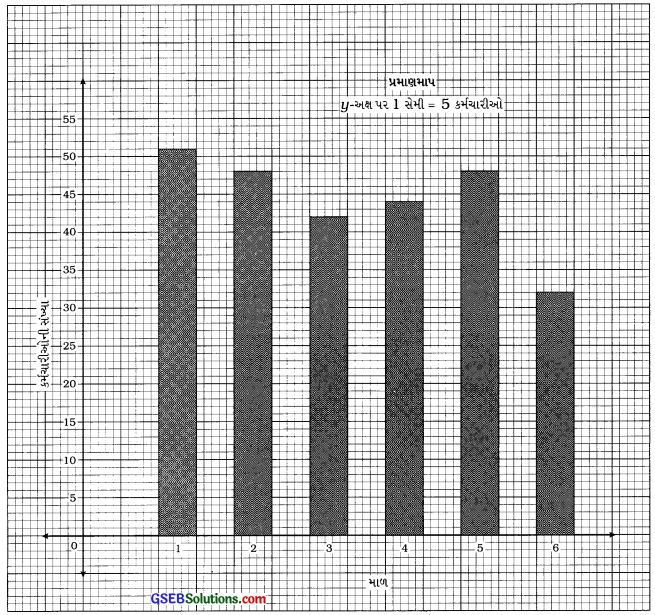
ઉદાહરણ : 1.
છ માળના એક વ્યાપારી-સંકુલના જુદા જુદા માળ પર કામ કરતા કર્મચારીઓની સંખ્યાનું આવૃત્તિ-વિતરણ નીચે મુજબ છેઃ

આપેલ માહિતીને લંબાલેખ દ્વારા રજૂ કરો.
ઉત્તર:

ઉદાહરણ : 2.
60 ગુણની પરીક્ષામાં 35 વિદ્યાર્થીઓએ મેળવેલ ગુણનું આવૃત્તિ-વિતરણ નીચે મુજબ છે :

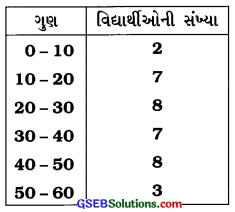
માહિતીને ખંભાલેખ દ્વારા રજૂ કરો.
ઉત્તર:

ઉદાહરણ : 3.
નીચેના આવૃત્તિ-વિતરણ પરથી ખંભાલેખ રચોઃ

ઉત્તર:

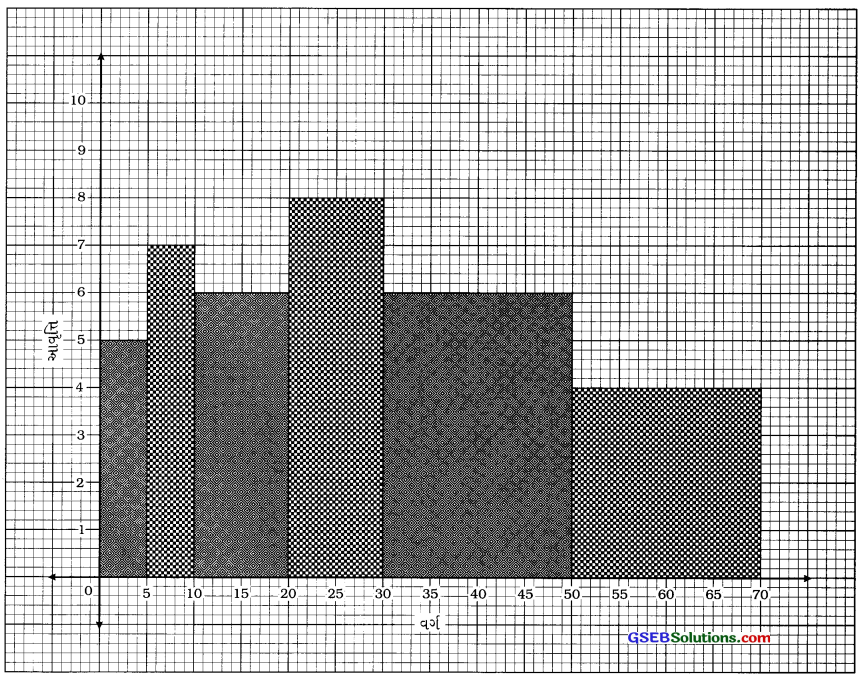
ઉદાહરણ : 4.
નીચેના આવૃત્તિ-વિતરણ માટે આવૃત્તિ-બહુકોણ રચોઃ

ઉત્તર:

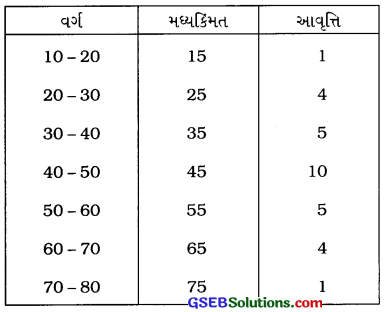
પ્રથમ વર્ગથી આગળના કાલ્પનિક વર્ગ 0 – 10ની મધ્યકિંમત 5 અને છેલ્લા વર્ગની પછીના કાલ્પનિક વર્ગની મધ્યકિંમત 85 છે.

→ મધ્યવર્તી સ્થિતિમાનનાં માપ (Measures of central Tendency) : સમગ્ર માહિતીની ખાસિયતો ધરાવતો અને સમગ્ર માહિતીનું પ્રતિનિધિત્વ કરતો આંક એટલે મધ્યવર્તી સ્થિતિમાન.

→ મધ્યવર્તી સ્થિતિમાન ત્રણ પ્રકારનાં છે :

1. મધ્યક,
2. મધ્યસ્થ અને
3. બહુલક.

→ મધ્યક (Mean) બધાં જ અવલોકનોની કિંમતના સરવાળાને અવલોકનોની કુલ સંખ્યા વડે ભાગતાં જે કિંમત મળે તેને આપેલ અવલોકનોનો મધ્યક અથવા સરેરાશ કહે છે.

મધ્યકને સંકેતમાં x̄ વડે દર્શાવાય છે. (વંચાય : x બાર) જો x₁, x₂, x₃, …………. x_n, એ n અવલોકનો હોય, તો આ બધાં અવલોકનોનો મધ્યક x̄ = \(\frac{x_{1}+x_{2}+x_{3}+\ldots+x_{n}}{n}\)

સરવાળા માટેની સંજ્ઞા તરીકે સંકેત Σ(વંચાય : સિગ્મા)નો ઉપયોગ કરાય છે.
x₁ + x₂ + x₃ + …………. + x_n ને .\(\sum_{i=1}^{n} x_{i}\) એ રીતે લખવામાં આવે છે.\(\sum_{i=1}^{n} x_{i}\) એટલે બધા x_i નો સરવાળો; જ્યાં, = 1,2,3…………,n છે.
આમ, મધ્યક (x̄) = \(\frac{\sum_{t=1}^{n} x_{i}}{n}\)

જો અવલોકનો સંખ્યામાં મોટા હોય, તો ધારેલા મધ્યકની રીતે મધ્યક શોધવામાં સરળતા રહે છે.
x̄ = A + \(\frac{\sum_{i=1}^{n} d_{i}}{n}\)
જ્યાં, A = ધારેલો મધ્યક,
d_i = x_i – A અને
n = અવલોકનોની સંખ્યા
i = 1, 2, 3, … n
x_i = અવલોકનો

→ અસતત આવૃત્તિ-વિતરણનો મધ્યકઃ જો x₁, x₂, x₃, …………. x_k અવલોકનોની આવૃત્તિઓ અનુક્રમે f₁, f₂, f₃, …………. f_n હોય, તો અસતત આવૃત્તિ-વિતરણનો મધ્યક નીચેના સૂત્રથી મળે :

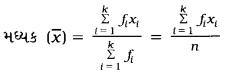
f_ix_i = મા અવલોકન અને તેની આવૃત્તિનો ગુણાકાર n = કુલ આવૃત્તિ
સતત ચલના આવૃત્તિ-વિતરણ માટે પણ ઉપરની રીતનો ઉપયોગ થઈ શકે. માત્ર સતત આવૃત્તિ-વિતરણમાં x_i એ માં વર્ગની મધ્યકિંમત સૂચવે છે.
વર્ગીકૃત માહિતીના મધ્યકની ગણતરી કરવામાં જો અવલોકનોની કિંમતો, મધ્યકિંમતો કે આવૃત્તિઓ મોટી સંખ્યામાં હોય, તો ગણતરી સરળ બનાવવા ધારેલા મધ્યકની રીતનો ઉપયોગ થાય છે.

→ મધ્યકના ગુણધર્મો :

• દરેક અવલોકનમાંથી મધ્યકને બાદ કરતાં મધ્યકને સાપેક્ષ વિચલન (Deviation) મળે અને આવા બધા વિચલનનો સરવાળો હંમેશાં શૂન્ય થાય, એટલે કે Σ (x_i – x̄) = 0.
• માહિતીના સૌથી નાના અને સૌથી મોટા અવલોકનની અસર મધ્યક પર ખૂબ જ પ્રબળ છે. જો માહિતી નાની હોય, તો મધ્યક એ સ્થિર માપ તરીકે ગણી શકાય.
• આપેલ માહિતી માટે,
  (a) જો દરેક અવલોકનમાં a ઉમેરવામાં આવે, તો નવાં અવલોકનોનો મધ્યક પણ 3 જેટલો વધે છે.
  (b) જો દરેક અવલોકનમાંથી બાદ કરવામાં આવે, તો નવાં અવલોકનોનો મધ્યક પણ 4 જેટલો ઘટે છે.
  (c) દરેક અવલોકનને d (a ≠ 0) વડે ગુણવામાં આવે, તો નવાં અવલોકનોનો મધ્યક વ ગણો થાય છે.
  (d) દરેક અવલોકનને \(\frac{1}{a}\) વડે ભાગવામાં આવે, તો મધ્યક – ગણો થાય છે. (a ≠ 0)
• જો એક માહિતીનાં n અવલોકનોનો મધ્યક x̄ હોય, તો આ અવલોકનોનો સરવાળો nx̄ થાય. બીજી માહિતીનાં m અવલોકનોનો મધ્યક ȳ હોય, તો આ અવલોકનોનો સરવાળો mȳ થાય. તેથી આપેલ (n + m) અવલોકનોનો સરવાળો (nx̄ + mȳ) થાય.
  ∴ બંને માહિતીનો સંયુક્ત મધ્યક \(\frac{n \bar{x}+m \bar{y}}{n+m}\) મળે.

→ મધ્યસ્થ (Median): માહિતીનાં અવલોકનોને ચડતા કે ઊતરતા ક્રમમાં ગોઠવ્યા પછી મધ્યમાં રહેલા અવલોકનને માહિતીનો મધ્યસ્થ કહે છે.
મધ્યસ્થને M વડે દર્શાવવામાં આવે છે.
જો અવલોકનોની સંખ્યા અયુગ્મ (એકી) હોય, તો મધ્યસ્થ (M) = \(\left(\frac{n+1}{2}\right)\)નું અવલોકન

જો અવલોકનોની સંખ્યા યુગ્મ (બેકી) હોય, તો

→ બહુલક (Mode) અવર્ગીકૃત માહિતીમાં સૌથી વધુ વખત પુનરાવર્તન પામતા અવલોકનને માહિતીનો બહુલક કહે છે. બહુલકને 2 વડે દર્શાવાય છે.

→ જો માહિતીનાં અવલોકનોમાં એક પણ અવલોકન પુનરાવર્તન , પામતું ન હોય, તો તેવી માહિતીને બહુલક નથી એમ કહેવાય.

→ જો માહિતીમાં બે કે તેથી વધુ અવલોકનો સરખી સંખ્યામાં પુનરાવર્તન પામતા હોય, તો તે દરેક અવલોકન તે માહિતીનો બહુલક છે.

→ માત્ર એક બહુલક ધરાવતી માહિતીને એક બહુલકીય (Unimodal) માહિતી કહે છે.

→ બે બહુલક ધરાવતી માહિતીને દ્વિબહુલકીય માહિતી (Bimodal). કહે છે.

→ બેથી વધારે બહુલક ધરાવતી માહિતીને બહુબહુલકીય (Multimodal) માહિતી કહે છે.

ઉદાહરણ : 1.
અવલોકનો 15, 22, 18, 27, 31, 21, 14, 16, 25 અને 34નો મધ્યક શોધો.
ઉત્તર:
મધ્યકx̄ = \(\frac{\Sigma x_{i}}{n}\) અહીં, n = 10 છે.
= \(\frac{15+22+18+27+31+21+14+36+25+34}{10}\)
= \(\frac{243}{10}\) = 24.3

ઉદાહરણ : 2.
30 વિદ્યાર્થીઓએ 50 ગુણની પરીક્ષામાં મેળવેલ ગુણનું આવૃત્તિ-વિતરણ નીચે પ્રમાણે છે :

ઉત્તર:
માહિતીનો મધ્યક શોધો.

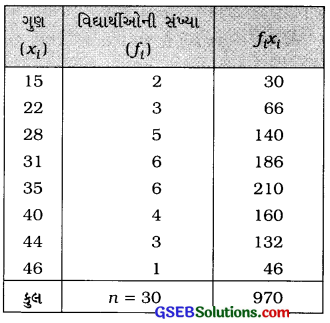
મધ્યક x̄ = \(\frac{\Sigma f_{i} x_{i}}{n}\)
= \(\frac{970}{30}\)
= 32\(\frac{1}{32}\) અથવા 32.33

ઉદાહરણ : 3.
11 વિદ્યાર્થીઓનાં વજન (કિગ્રામાં નીચે મુજબ છે :
37, 42, 40, 39, 41, 35, 37, 30, 40, 40, 42.
આ માહિતીનો મધ્યસ્થ શોધો.
ઉત્તર:
અવલોકનોને ચડતા ક્રમે ગોઠવતાં નીચે મુજબની ગોઠવણી મળે ? 35, 36, 37, 37, 39, 40, 40, 40, 41, 42, 42 અહીં, n =11 એ અયુગ્મ છે.
∴ મધ્યસ્થ M = \(\left(\frac{n+1}{2}\right)\) અવલોકન
= \(\left(\frac{11+1}{2}\right)\)મું અવલોકન
= 6મું અવલોકન
= 40
આમ, માહિતીનો મધ્યસ્થ 40 કિગ્રા છે.

ઉદાહરણ : 4.
અવલોકનો 62, 67, 82, 71, 75, 77, 83, 91નો મધ્યસ્થ શોધો.
ઉત્તર:
અવલોકનોને ચડતા ક્રમે ગોઠવતાં નીચે મુજબની ગોઠવણી મળે : 62, 63, 67, 71, 75, 77, 82, 91 અહીં, n = 8 એ યુગ્મ છે.

= 73 આમ, આપેલ અવલોકનોનો મધ્યસ્થ 73 છે.

ઉદાહરણ : 5.
નીચેનાં અવલોકનોનો બહુલક શોધોઃ
14, 25, 28, 29, 17, 14, 19, 22, 14, 30, 16, 28, 14, 25.
ઉત્તર:
અહીં, માહિતીનું અવલોકન કરતાં પ્રથમ નજરે જ સ્પષ્ટ જણાય છે કે અવલોકન 14 ચાર વખત આવે છે. એટલે કે માહિતીમાં અવલોકન 14 સૌથી વધુ 4 વખત પુનરાવર્તિત થાય છે. આથી માહિતીનો બહુલક 14 છે.