This GSEB Class 9 Maths Notes Chapter 5 યુક્લિડની ભૂમિતિનો પરિચય covers all the important topics and concepts as mentioned in the chapter.
યુક્લિડની ભૂમિતિનો પરિચય Class 9 GSEB Notes
→ ભૂમિતિને અંગ્રેજીમાં Geometry કહે છે. Geometry શબ્દ બે ગ્રીક શબ્દના સંયોજનથી બનેલો છે. Geo અને Metrein. Geoનો અર્થ પૃથ્વી અને Metreinનો અર્થ માપ થાય.
→ ગ્રીક ગણિતશાસ્ત્રી થેલ્સને ભૂમિતિના પ્રણેતા ગણવામાં આવે છે. સૌપ્રથમ ભૂમિતિ શબ્દનો પ્રયોગ તેમણે કર્યો હતો. થેલ્સના વિદ્યાર્થી પાયથાગોરસ અને તેના સાથીદારોએ ભોમિતિક બાબતો શોધી હતી.
→ ઈ. સ. પૂર્વે 800થી ઈ. સ. પૂર્વે 500ના ગાળામાં સૂલબાસૂત્રનું સર્જન થયું હતું. બોધાયન સૂલબાસૂત્ર સૌથી પ્રાચીન છે, તેમાંની રચનામાં પાયથાગોરસના સિદ્ધાંતની સાબિતીનો ઉપયોગ થયો હતો. જાહેર પ્રાર્થનાસભાઓમાં લંબચોરસ, ત્રિકોણ અને સમલંબ ચતુષ્કોણ જેવા આકારનાં આસનોનો ઉપયોગ થતો હતો. આમ, ભારતીયો પાયથાગોરસના પ્રમેયને પાયથાગોરસના જન્મ પહેલાંથી જાણે છે. આર્યભટ્ટ, બ્રહ્મગુપ્ત, ભાસ્કરાચાર્ય વગેરે ભારતના ગણિતશાસ્ત્રીઓએ ભૂમિતિના વિકાસમાં ફાળો આપેલ છે.
![]()
→ ઘન પદાર્થની ધાર એ અવકાશનું વિભાજન કરતી સપાટીઓ છે. સપાટીને જાડાઈ હોતી નથી. સપાટીની ધાર વક્ર કે રેખા હોય છે. રેખા અંતે તો બિંદુમાં પરિણમે છે. ઘનથી બિંદુ સુધી ક્રમશઃ આગળ વધતાં પરિમાણ ઘટતું જાય છે.
| ભૌમિતિક પદાર્થ | પરિમાણો |
| ઘન | 3 |
| સપાટી | 2 |
| રેખા | 1 |
| બિંદુ | એક પણ નહિ |
→ યુક્લિડ ઈજિપ્તમાં એલેક્ઝાન્ડ્રિયાની શાળામાં ગણિતના શિક્ષક હતા. તેમણે પૂર્વધારણાઓ અને અગાઉ સિદ્ધ કરેલાં પરિણામોને આધારે તાર્કિક સાબિતીઓ આપી ભૂમિતિનો વિકાસ કર્યો. તેમણે “Elements’ નામના પુસ્તકમાં ભૂમિતિ વિશે 13 પ્રકરણો લખ્યાં હતાં. તેમણે પ્રથમ પ્રકરણમાં 23 વ્યાખ્યાઓ આપેલી જેમાંથી કેટલીક નીચે દર્શાવી છેઃ
- બિંદુને કોઈ ભાગ નથી.
- રેખા એ પહોળાઈ વગરની લંબાઈ છે.
- રેખાને અંત્યબિંદુઓ હોય છે.
- જે પોતાના પરનાં બિંદુઓની સાથે સમાન રીતે રહેલી હોય એવી રેખા એક સીધી રેખા છે.
- પૃષ્ઠને માત્ર લંબાઈ અને પહોળાઈ હોય છે. રિલીઝ થઇ .
- પૃષ્ઠની ધાર રેખાઓ હોય છે.
- જે સપાટી પોતાના પરની સીધી રેખાઓની સાથે એકસમાન રીતે રહેલ હોય તેવી સપાટી એ સમતલ છે.
→ યુક્લિડે નોંધેલા સ્વયંસિદ્ધ સત્યો નીચે પ્રમાણે વર્ણવી શકાય:
- એક વસ્તુને સમાન હોય તેવી વસ્તુઓ એકબીજાને સમાન થાય.
- સરખામાં સરખું ઉમેરીએ તો સરવાળા સરખા રહે.
- સરખામાંથી સરખા બાદ કરીએ તો બાદબાકી (શેષફળ) સરખી રહે.
- એકબીજા ઉપર બંધબેસતી આવતી વસ્તુઓ એકબીજાને સરખી થાય.
- આખું તેના ભાગ કરતાં મોટું હોય છે.
- સરખી વસ્તુઓના બમણા એકબીજાને સમાન થાય.
- સરખી વસ્તુઓના અડધા એકબીજાને સમાન થાય.
→ યુક્લિડની પાંચ પૂર્વધારણાઓ નીચે પ્રમાણે છે:
- પૂર્વધારણા : એક બિંદુમાંથી બીજા બિંદુમાં થઈને પસાર થતી એક સીધી રેખા દોરી શકાય.
પૂર્વધારણા 5.1: આપેલાં બે ભિન્ન બિંદુઓમાંથી પસાર થતી અનન્ય રેખા હોય છે. - પૂર્વધારણા 2 સાન્ત રેખાને અનંત સુધી લંબાવી શકાય છે. નોંધઃ યુક્લિડ રેખાખંડ માટે “સાન્ત રેખા’ શબ્દ પ્રયોજતા હતા.
- પૂર્વધારણા 3: કોઈ પણ બિંદુને કેન્દ્ર લઈ તથા કોઈ પણ લંબાઈની ત્રિજ્યા લઈ વર્તુળ રચી શકાય.
- પૂર્વધારણા 4: બધા જ કાટખૂણા એકબીજા સાથે સરખા થાય.
- પૂર્વધારણા 5: જો બે રેખાઓને કોઈ ત્રીજી રેખા છેદે અને આ રેખાની એક જ બાજુ તરફના બે અંતઃકોણોનો સરવાળો બે કાટખૂણાના સરવાળા કરતાં ઓછો હોય, તો પ્રથમ બે રેખાઓને આ ખૂણાઓ તરફ અનંત સુધી લંબાવતાં તેઓ એકબીજાને છેદે છે.
![]()
→ બે પરસ્પર છેદતી રેખાઓમાંની બંને એકસાથે આપેલ રેખાને સમાંતર હોઈ શકે નહિ.
→ પ્રમેય : બે ભિન્ન રેખાઓમાં એકથી વધુ સામાન્ય બિંદુ ન હોઈ શકે.
ઉદાહરણ : 1.
જો P, Q અને R એક રેખા પર આવેલાં ત્રણ બિંદુઓ હોય P અને Q બિંદુ એ P અને Rની વચ્ચે આવેલ હોય, તો સાબિત કરો કે, PQ + QR = PR.
ઉત્તર:
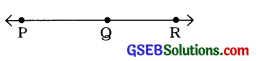
ઉપરની આકૃતિમાં PQ + QRની સાથે PR સંપાતિ છે. યુક્લિડના ૬ સ્વયંસિદ્ધ સત્ય (4) મુજબ વસ્તુઓ જો પરસ્પર બંધબેસતી હોય તો તે એકબીજાની બરાબર હોય. આથી સાબિત થાય છે કે, PQ + QR = PR.
→ યુક્લિડની પાંચમી પૂર્વધારણાને સમકક્ષ વિધાનો યુક્લિડની પાંચમી પૂર્વધારણાને સમકક્ષ અનેક વિધાનો છે. તેમાંથી એક પ્લેફેરની પૂર્વધારણા (Playfair’s axiom) અગત્યનું છે.
→ પ્લેફેરની પૂર્વધારણા દરેક રેખા l અને તેના પર ન હોય તેવા પ્રત્યેક બિંદુ P માટે એક અનન્ય રેખા જો એવી હોય છે, જે Pમાંથી પસાર થાય છે અને lને સમાંતર છે. બીજા શબ્દોમાં, બે ભિન્ન અને એકબીજાને છેદતી રેખાઓ એક જ રેખાને સમાંતર હોઈ શકે નહિ.
→ અયુક્લિડ ભૂમિતિ (Non-Euclidean geometry): અનેક ગણિતશાસ્ત્રીઓ અને યુક્લિડને પોતાને વિશ્વાસ હતો કે પાંચમી પૂર્વધારણા પ્રમેય છે અને સાબિત કરી શકાય. પરંતુ તેની સાબિતી મેળવવાના પ્રયત્નોમાં યુક્લિડની ભૂમિતિથી અલગ હોય તેવી ભૂમિતિઓનો ઉદય થયો. આ બધી ભૂમિતિઓને અયુક્લિડીય ભૂમિતિ કહે છે. તેમાંની એક અગત્યની ભૂમિતિ ગોલીય ભૂમિતિ (Spherical geometry) છે. ગોલીય ભૂમિતિમાં રેખાઓ સીધી હોતી નથી. રેખાઓ દીર્ઘ વર્તુળો(Great circles)ના ભાગ હોય છે. ગોલીય ભૂમિતિમાં ત્રિકોણના ત્રણ ખૂણાઓનો સરવાળો 180°થી વધારે થાય છે. યુક્લિડીય ભૂમિતિ માત્ર એક જ સમતલમાં બનતી આકૃતિઓ માટે જ માન્ય છે. વક્રસપાટીમાં તે નિષ્ફળ જાય છે.