This GSEB Class 9 Maths Notes Chapter 9 સમાંતરબાજુ ચતુષ્કોણ અને ત્રિકોણનાં ક્ષેત્રફળ covers all the important topics and concepts as mentioned in the chapter.
સમાંતરબાજુ ચતુષ્કોણ અને ત્રિકોણનાં ક્ષેત્રફળ Class 9 GSEB Notes
→ સમતલીય પ્રદેશ સરળ બંધ આકૃતિ દ્વારા ઘેરાયેલા સમતલ ભાગને તે આકૃતિનો સમતલીય પ્રદેશ (Planar region) કહેવાય છે.
→ આકૃતિનું ક્ષેત્રફળઃ સરળ બંધ આકૃતિના સમતલીય પ્રદેશના પરિમાણ (Magnitude) કે માપ(Measure)ને આકૃતિનું ક્ષેત્રફળ (Area) કહે છે. આ પરિમાણ કે માપને હંમેશાં એક ધન વાસ્તવિક સંખ્યા કોઈક એકમ(Unit)માંની મદદથી દર્શાવવામાં આવે છે.
→ એકરૂપ આકૃતિઓનાં ક્ષેત્રફળ ઃ જો બે આકૃતિઓ A અને B એકરૂપ હોય, તો તેમનાં ક્ષેત્રફળ પણ ચોક્કસ સમાન જ હોય. તેમ છતાં, આથી ઊલટું વિધાન સત્ય નથી. એટલે કે, સમાન ક્ષેત્રફળ ધરાવતી બે આકૃતિઓ એકરૂપ હોય તે જરૂરી નથી.
→ આકૃતિના ક્ષેત્રફળનો સંકેત આકૃતિ Aના ક્ષેત્રફળને સંકેત ar (A) દ્વારા દર્શાવવામાં આવે છે.
→ આકૃતિના ક્ષેત્રફળના ગુણધર્મો :
- જો A અને B એકરૂપ આકૃતિઓ હોય, તો ar (A) = ar (B).
- જો આકૃતિ T દ્વારા બનતો સમતલીય પ્રદેશ, બે આકૃતિઓ P અને B દ્વારા બનતા એકબીજાને આચ્છાદિત ન કરે (Non-overlaping) તેવા સમતલીય પ્રદેશો ભેગા થઈને બને, તો ar (T) = ar (P) + ar (Q).
![]()
→ એક જ પાયા પર અને સમાંતર રેખાઓ વચ્ચેની આકૃતિઓઃ જો બે આકૃતિઓને એક સામાન્ય પાયો (બાજુ) હોય અને શિરોબિંદુઓ (અથવા શિરોબિંદુ) દરેક આકૃતિનાં સામાન્ય પાયાની એક જ બાજુએ, પાયાને સમાંતર રેખા પર હોય, તો બે આકૃતિઓ સમાન પાયા પર અને સમાંતર રેખાઓની એક જોડ વચ્ચે આવેલી છે તેમ કહેવાય. નોંધઃ બે સમાંતર રેખાઓમાંથી એક રેખા સામાન્ય પાયામાંથી પસાર થતી હોવી જોઈએ.
→ એક જ પાયા પર અને સમાંતર રેખાની જોડ વચ્ચેના સમાંતરબાજુ ચતુષ્કોણ:
પ્રમેય 9.1 એક જ પાયા (અથવા સમાન પાયા) પર આવેલા અને બે સમાંતર રેખાઓની એક જોડ વચ્ચે આવેલા સમાંતરબાજુ ચતુષ્કોણોનાં ક્ષેત્રફળ સમાન હોય છે.
→ સમાંતરબાજુ ચતુષ્કોણનું ક્ષેત્રફળ તેના પાયા અને પાયાને અનુરૂપ વેધના ગુણાકાર જેટલું હોય છે.
→ એક જ પાયા (અથવા સમાન પાયા) પર અને પાયાની એક જ બાજુએ આવેલા અને સમાન ક્ષેત્રફળવાળા સમાંતરબાજુ ચતુષ્કોણો એ સમાંતર રેખાઓની જોડની રેખાઓ વચ્ચે આવેલા હોય છે, જે પૈકી એક પાયાને સમાવતી રેખા છે.
→ જો ત્રિકોણ અને સમાંતરબાજુ ચતુષ્કોણ એક જ પાયા પર અને બે સમાંતર રેખાઓની એક જોડની રેખાઓ વચ્ચે આવેલા હોય, તો ત્રિકોણનું ક્ષેત્રફળ સમાંતરબાજુ ચતુષ્કોણના ક્ષેત્રફળ કરતાં અડધું હોય છે.
ઉદાહરણ : 1.
આપેલ આકૃતિમાં સમલંબ ચતુષ્કોણ ABCDમાં AB ∥ DC છે. BCને લંબાવી તેના પર બિંદુ E લીધેલ છે. સાબિત કરો 3, ar (BDE) = ar (ACED).
ઉત્તર:
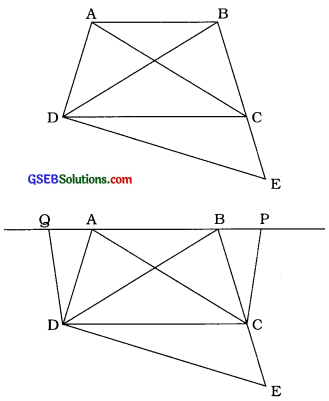
C માંથી ADને સમાંતર રેખા દોરો, જે રેખા ABP Pમાં છે. આથી સમાંતરબાજુ ચતુષ્કોણ ADCP મળે.
Dમાંથી BCને સમાંતર રેખા દોરો, જે રેખા ABને ઉમાં છેદે. આથી સમાંતરબાજુ ચતુષ્કોણ BCDQ મળે.
અહીં, સમાંતરબાજુ ચતુષ્કોણ ADCP અને BCDQ સમાન પાયા DC પર આવેલા અને સમાંતર રેખાઓની જોડ DC ∥ PQ વચ્ચે આવેલા છે.
∴ ar (ADCP) = ar (BCDQ) …………. (1)
સમાંતરબાજુ ચતુષ્કોણનો વિકર્ણ તેનું બે એકરૂપ ત્રિકોણોમાં વિભાજન કરે છે.
∴ ar (ADC) = \(\frac{1}{2}\)ar (ADCP) અને
ar (BCD) = \(\frac{1}{2}\) ar (BCDQ) ……. (2)
(1) અને (2) પરથી,
ar (ADC) = ar (BCD)
∴ ar (ADC) + ar (DCE) = ar (BCD) + ar (DCE)
∴ ar (ACED) = ar (BDE) (પરસ્પર આચ્છાદિત ન કરે તેવા પ્રદેશો)
∴ ar (BDE) = ar (ACED)
નોંધ: ઉપરોક્ત દાખલામાં ar (ADC) = ar (BCD) એ પ્રમેય 9.2નું પરિણામ છે, એટલે કે સમગ્ર પ્રકરણના અભ્યાસ બાદ આ દાખલામાં તે ભાગ સાબિત ન કરવો પડે.
ઉદાહરણ : 2.
સમાંતરબાજુ ચતુષ્કોણ ABCDમાં AB = 12 સેમી. AB અને BCને અનુરૂપ વેધ અનુક્રમે DM અને DN છે. જો DM = 5 સેમી અને DN = 6 સેમી હોય, તો BC શોધો.
ઉત્તર:
સમાંતરબાજુ ચતુષ્કોણનું ક્ષેત્રફળ તેના પાયા અને અનુરૂપ વેધના ગુણાકાર જેટલું હોય છે. અહીં, સમાંતરબાજુ ચતુષ્કોણ ABCDમાં પાયા ABને અનુરૂપ વેધ DM તથા પાયા BCને અનુરૂપ વેધ Dય છે.
∴ ar (ABCD) = AB × DM = BC × DN
∴AB × DM = BC × DN
∴ 12 × 5 = BC × 6
∴60 = BC × 6
∴BC = 9
∴ BC = 10 સેમી
![]()
ઉદાહરણ : 3.
જો E, F G અને H એ અનુક્રમે સમાંતરબાજુ ચતુષ્કોણ ABCDની બાજુઓનાં મધ્યબિંદુઓ હોય, તો સાબિત કરો કે ar(EFGH) = \(\frac{1}{2}\) ar (ABCD).
ઉત્તર:
સમાંતરબાજુ ચતુષ્કોણ ABCDની બાજુઓ AB, BC, CD અને DAનાં મધ્યબિંદુઓ અનુક્રમે E, F G અને H છે. GE દોરો.
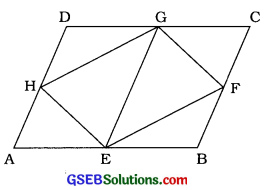
સમાંતરબાજુ ચતુષ્કોણ ABCDમાં AB ∥ CD અને AB = CD
∴ BE ∥ CG અને BE (\(\frac{1}{2}\)AB) = CG (\(\frac{1}{2}\)CD)
ચતુષ્કોણ EBCG એ સમાંતરબાજુ ચતુષ્કોણ છે.
∴ GE ∥ BC
હવે, ∆EFG અને સમાંતરબાજુ ચતુષ્કોણ EBCG એક જ પાયા GE પર અને સમાંતર રેખાઓની એક જોડ GE ∥BC વચ્ચે આવેલાં છે.
∴ ar (ENG) = \(\frac{1}{2}\)ar (EBCG) ……. (1)
તે જ રીતે, ∆EHG અને સમાંતરબાજુ ચતુષ્કોણ AEGD એક જ પાયા GE પર અને સમાંતર રેખાઓની એક જોડ GE ∥ DA વચ્ચે આવેલાં છે.
∴ ar (EHG) = \(\frac{1}{2}\)ar (AEGD) ……. (2)
પરિણામ (1) અને (2)નો સરવાળો લેતાં,
∴ ar (EFG) + ar (EHG) = \(\frac{1}{2}\)ar (EBCG) + \(\frac{1}{2}\)ar (AEGD)
∴ ar (EFGH) = \(\frac{1}{2}\)[ar (EBCG) + ar (AEGD)].
∴ ar (EFGH) = \(\frac{1}{2}\) ar (ABCD)
ઉદાહરણ : 4.
આપેલ આકૃતિમાં P એ સમાંતરબાજુ ચતુષ્કોણ ABCDના અંદરના ભાગમાં આવેલું કોઈ બિંદુ છે, તો સાબિત કરો કે
(1) ar (APB) + ar (PCD) = \(\frac{1}{2}\)ar (ABCD)
(2) ar (APD) + ar (PBC) = ar (APB) + or (PCD) (સૂચનઃ Pમાંથી પસાર થતી અને ABને સમાંતર એક રેખા દોરો.)
ઉત્તર:
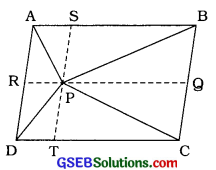
Pમાંથી પસાર થતી અને ABને સમાંતર એક રેખા દોરો, જે ? BCને 9માં અને ADને Rમાં છે.
હવે, ચતુષ્કોણ ABQRમાં,
AB ∥ OR (રચના મુજબ)
BQ ∥ AR (સમાંતરબાજુ ચતુષ્કોણ ABCDમાં BC ∥ AD)
∴ ચતુષ્કોણ ABQR સમાંતરબાજુ ચતુષ્કોણ છે. તે જ રીતે DCQR પણ સમાંતરબાજુ ચતુષ્કોણ છે.
∆APB અને સમાંતરબાજુ ચતુષ્કોણ ABOR એક જ પાયા AB પર અને સમાંતર રેખાઓની એક જોડ AB ∥ OR વચ્ચે આવેલાં છે.
∴ ar (APB) = \(\frac{1}{2}\)ar (ABQR) …… (1)
તે જ રીતે, A PCD અને સમાંતરબાજુ ચતુષ્કોણ DCQR એક જ પાયા DC પર અને સમાંતર રેખાઓની એક જોડ DC ∥ OR વચ્ચે આવેલાં છે.
∴ ar (PCD) = \(\frac{1}{2}\)ar (DCOR) …….. (2)
પરિણામ (1) અને (2)નો સરવાળો લેતાં,
∴ ar (APB)+ ar (PCD)
= \(\frac{1}{2}\)ar (ABOR) + \(\frac{1}{2}\)ar (DCQR)
∴ ar (APB) + ar (PCD)
= \(\frac{1}{2}\)[ar (ABQR) + ar (DCQR)]
∴ar (APB)+ ar (PCD) = \(\frac{1}{2}\)ar (ABCD) ..(3)
હવે, Pમાંથી પસાર થતી અને ADને સમાંતર એક રેખા દોરો, જે ABને Sમાં અને CDને Tમાં છેદે.
તો ઉપર મુજબ જ સાબિત થાય છે, ar (APD)+ ar (PBC) = \(\frac{1}{2}\)ar (ABCD) … (4)
(3) અને (4) પરથી,
∴ ar (APD)+ ar (PBC) = ar (APB)+ ar (PCD)
→ એક જ પાયા પર આવેલા અને સમાંતર રેખાઓની જોડની રેખાઓ વચ્ચે આવેલા ત્રિકોણ:
પ્રમેય 9.2: એક જ પાયા (અથવા સમાન પાયા) પર આવેલા અને બે સમાંતર રેખાઓની જોડની રેખાઓ વચ્ચે આવેલા બે ત્રિકોણનાં ક્ષેત્રફળ સમાન હોય છે.
→ ત્રિકોણનું ક્ષેત્રફળ : ત્રિકોણનું ક્ષેત્રફળ, તેનો પાયો અને તે પાયાને અનુરૂપ વેધના ગુણાકારથી અડધું હોય છે.
→ પ્રમેય 9.3: એક જ પાયા (સમાન પાયા) પર આવેલા અને એક જ પાયા(સમાન પાયા)ની એક જ બાજુએ આવેલા તથા સમાન ક્ષેત્રફળ ધરાવતા ત્રિકોણો બે સમાંતર રેખાઓની જોડની રેખાઓ વચ્ચે આવેલા હોય છે, જેમાંની એક રેખા પાયાને સમાવતી રેખા છે.
→ ત્રિકોણની મધ્યગાનો ગુણધર્મઃ ત્રિકોણની કોઈ પણ મધ્યગા, તેનું બે સમાન ક્ષેત્રફળોવાળા ત્રિકોણોમાં વિભાજન કરે છે.
![]()
ઉદાહરણ : 1.
∆ABCમાં P અને Q એ BCનાં ત્રિભાગ બિંદુઓ છે. સાબિત કરો કે,
ar (ABP) = ar (APC) = ar (AGC) = \(\frac{1}{3}\)ar (ABC).
ઉત્તર:
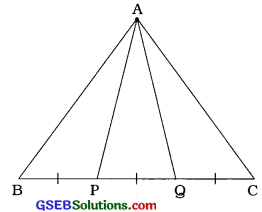
P અને Q એ BCનાં ત્રિભાગ બિંદુઓ છે.
∴ BP = PQ = QC
∴ P એ Bઉનું અને એ PCનું મધ્યબિંદુ છે.
આથી ∆ABQમાં AP મધ્યગા છે.
∴ ar (ABP) = ar (APQ)…………(1)
તે જ રીતે, ∆APCમાં AQ મધ્યગા છે.
∴ ar (APQ) = ar (ABC) ……..(2)
આમ, (1) અને (2) પરથી,
∴ ar (ABP) = ar (APQ) = ar (AQC) … (3)
વળી, ∆ABP, ∆APQ અને ∆AQC એ પરસ્પર આચ્છાદિત ન થતા હોય તેવા પ્રદેશો છે.
∴ ar (ABP) + ar (APQ) + ar (AQC) = ar (ABC) ……(4)
(3) અને (4) પરથી,
ar (ABP) = ar (APQ) = ar (AQC) = \(\frac{1}{3}\)ar (ABC).
ઉદાહરણ : 2.
∆ABCની બાજુઓ BC, CA અને IBનાં મધ્યબિંદુઓ અનુક્રમે D, E અને F છે, તો સાબિત કરો કે
(i) BDEF એક સમાંતરબાજુ ચતુષ્કોણ છે.
(ii) ar (DEF) = ar (ABC)
(iii) ar (BDEF) = \(\frac{1}{2}\)ar (ABC)
ઉત્તર:
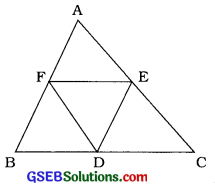
∆ABCમાં F અને E અનુક્રમે AB અને ACનાં મધ્યબિંદુઓ છે.
∴ FE ∥ BC એટલે કે, FE ∥ BD
∆ABCમાં E અને D અનુક્રમે AC અને BCનાં મધ્યબિંદુઓ છે.
∴ ED ∥ AB. એટલે કે, ED ∥ FB
ચતુષ્કોણ BDEFમાં FE ∥ BD 24 ED ∥ FB
ચતુષ્કોણ BDEF એક સમાંતરબાજુ ચતુષ્કોણ છે … પરિણામ (1)
તે જ પ્રમાણે, ચતુષ્કોણ AFDE અને ચતુષ્કોણ FDCE ‘સમાંતરબાજુ ચતુષ્કોણ છે.
સમાંતરબાજુ ચતુષ્કોણ BDEFમાં FD વિકર્ણ હોવાથી
ar (BDF) = ar (DEF) … (1)
સમાંતરબાજુ ચતુષ્કોણ AFDEમાં EF વિકર્ણ હોવાથી
ar (AFE) = ar (DEF) … … (2)
સમાંતરબાજુ ચતુષ્કોણ FDCEમાં ED વિકર્ણ હોવાથી
ar (DCE) = ar (DEF) …. (3)
∆ABC એ એકબીજાને આચ્છાદિત ન કરે તેવા ∆BDF ∆AFE, ∆DCE અને ∆DEF દ્વારા બને છે.
∴ ar (ABC) = ar (BDF) + ar (AFE) + ar (DCE) + ar (DEF).
∴ ar (ABC). = ar (DEF) + ar (DEF) + ar (DEF) + ar (DEF) [1), (2) અને (3) પરથી]
∴ ar (ABC) = 4ar (DEF)
∴ ar (DEF) = ar (ABC) … પરિણામ (ii)
હવે, ar (BDEF) = ar (BDF) + ar (DEF)
∴ ar (BDEF) = ar (DEF) + ar (DEF)
∴ ar (BDEF) = 2ar (DEF)
∴ ar (BDEF) = 2 × \(\frac{1}4}\)ar (ABC)
∴ ar (BDEF) = \(\frac{1}{2}\)ar (ABC) …. પરિણામ (iii)