GSEB Class 9 Science Important Questions Chapter 11 કાર્ય અને ઊર્જા

Gujarat Board GSEB Class 9 Science Important Questions Chapter 11 કાર્ય અને ઊર્જા Important Questions and Answers.

GSEB Class 9 Science Important Questions Chapter 11 કાર્ય અને ઊર્જા

વિશેષ પ્રશ્નોત્તર
નીચેના દાખલા ગણો

પ્રશ્ન 1.
15 kg દળવાળા એક પદાર્થને 40 m જેટલું અધોદિશામાં છે સ્થાનાંતર ગુરુત્વાકર્ષણના બળની અસર હેઠળ આપવામાં આવે છે, તો થયેલું કાર્ય ગણો. (g = 10 m s^-2 લો.)
ઉત્તર:
6000

પ્રશ્ન 2.
120 g દળવાળા એક પદાર્થને ઊર્ધ્વદિશામાં 5 mની ઊંચાઈ સુધી લઈ જવામાં આવે છે, તો કાર્યની ગણતરી કરો. g = 10 m^-2).
ઉત્તર:
– 6 J

પ્રશ્ન ૩.
60 kg દળવાળી વ્યક્તિએ 750 J ગતિ-ઊર્જા પ્રાપ્ત કરવા માટે કેટલી ઝડપથી દોડવું જોઈએ?
ઉત્તર:
5 m s^-1

પ્રશ્ન 4.
1000 kg દળવાળી એક મોટરકાર 1,12,500 J ગતિ-ઊર્જા ધરાવે છે. સામે અવરોધ દેખાતાં ચાલક બ્રેક લગાવે છે અને કાર 100 મીટર અંતર કાપીને ઊભી રહે છે (અકસ્માત કર્યા વગર), તો ઘર્ષણબળ શોધો.
ઉત્તર:
1125 N

પ્રશ્ન 5.
50 kg દળવાળી હેતસ્વી 30 kg દળ લઈને 20 m ઊંચાઈ સુધી 40 sમાં ચઢે છે, તો પાવર અને થતા કાર્યની ગણતરી કરો. g = 10 m s^-2).
ઉત્તર:
16000 J, 400 w

પ્રશ્ન 6.
40 ની 5 ટ્યૂબલાઇટ 10 કલાક ચાલુ રાખતાં વપરાતી વિદ્યુત-ઊર્જા યુનિટમાં ગણો.
ઉત્તર:
2 યુનિટ

પ્રશ્ન 7.
40 kg દળનો એક બાળક 0.2 m ઊંચાઈવાળાં 30 પગથિયાં 30 sમાં ચઢે છે, તો પાવર ગણો. (g = 9.8 m s^-2)
ઉત્તર:
78.4 w

પ્રશ્ન 8.
એક સ્ત્રી 10 kg દળવાળી પાણીની ડોલ 8m ઊંડા કૂવામાંથી 20 sમાં ઉપર ખેંચે છે, તો થતું કાર્ય અને પાવર ગણો. (g = 10 m s^-2).
ઉત્તર:
800 J, 40 w

પ્રશ્ન 9.
1000 kg દળની એક કાર 36 km h^-1ની ઝડપથી ગતિ કરે છે, તો તેનું વેગમાન અને ગતિ-ઊર્જા ગણો.
(અહીં મળતી ગતિ-ઊર્જાનું મૂલ્ય K = p²|2 m થી ચકાસો. p વેગમાન છે. K = p² / 2 m કેવી રીતે થાય? વિચારો.)
Hint: p = mv અને E = \(\frac{1}{2}\) mv² સૂત્રો વાપરો.
E_k = \(\frac{1}{2}\)mv² × \(\frac{m}{m}\) = \(\frac{1}{2} \frac{m^{2} v^{2}}{m}\) = \(\frac{p^{2}}{2 m}\)
ઉત્તર:
10,000 kg m s^-1, 50,000 J

પ્રશ્ન 10.
નીચેની આકૃતિમાં દર્શાવેલ એક લોલકને સમક્ષિતિજ રાખેલ છે. તેને તે સ્થિતિમાંથી મુક્ત કરતાં નિમ્નતમ સ્થિતિમાં તેનો વેગ કેટલો થાય? (g = 9.8 m s^-2)

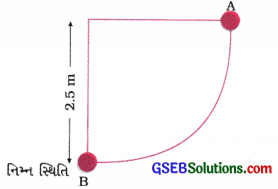
Hint: (ગતિ-ઊર્જા)_{B સ્થાને} = સ્થિતિ-ઊર્જા_{A સ્થાને}

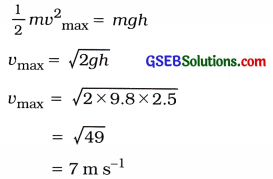
ઉત્તર:
7 m s^-1

પ્રશ્ન 11.
એક ઘરમાં 40 % ની એક એવી 4 ટ્યૂબલાઇટ દરરોજ 5 કલાક ચાલે છે અને 120 wનો એક એવા 3 પંખા રોજના 4 કલાક ચાલે છે, તો સપ્ટેમ્બર માસ માટે યુનિટના ૨ 5 પ્રમાણે વીજળી વપરાશનું બિલ કેટલું થાય?
Hint: એક દિવસમાં ચાર ટ્યૂબલાઇટ દ્વારા ખર્ચાતી વિદ્યુત
ઊર્જા = 4 × 40 W × 5 h = 800 Wh

→ એક દિવસમાં ત્રણ પંખા દ્વારા ખર્ચાતી વિદ્યુત-ઊર્જા
= 3 × 120 W × 4 h
= 1440 Wh

→ એક દિવસમાં વપરાતી કુલ વિદ્યુત-ઊર્જા
= 800 Wh + 1440 Wh
= 2240 Wh
= 2.240 × 10³ Wh
= 2.24 kWh
= 2.24 યુનિટ (∵ 1 kWh = 1 યુનિટ)

→ સપ્ટેમ્બર માસમાં ખર્ચાતા કુલ યુનિટ
= 30 × 2.24
= 67.2 યુનિટ

→ વીજળી વપરાશનું બિલ
= 5 × 67.2
= 336 રૂપિયા
ઉત્તર:
336 રૂપિયા

પ્રશ્ન 12.
એક રૉકેટ ઊર્ધ્વદિશામાં ઇ વેગથી ગતિ કરે છે, તેનો વેગ અચાનક ત્રણ ગણો થાય, તો તેની પ્રારંભિક અને અંતિમ ગતિ-ઊર્જાનો ગુણોત્તર શોધો.
Hint: અહીં રૉકેટનું દળ ‘m અચળ છે. રૉકેટની ગતિ-ઊર્જા
E_K = \(\frac{1}{2}\) mv² સૂત્ર પરથી, E_k ∝ v²
ઉત્તર:
1 : 9

પ્રશ્ન 13.
અવિનાશ તેના પર લાગતાં 10 N જેટલા ઘર્ષણબળ વિરુદ્ધ
8 m s^-1 જેટલા વેગથી ગતિ કરે છે અને કપિલ તેના પર લાગતાં 25 N જેટલા ઘર્ષણબળ વિરુદ્ધ 3 m s^{– 1} જેટલા વેગથી ગતિ કરે છે. તો બંનેમાંથી કોનો પાવર વધુ હશે?
Hint: પાવર P = (બળ F) (વેગ ) સૂત્ર વાપરો.
ઉત્તર:
અવિનાશનો પાવર વધુ હશે.

પ્રશ્ન 14.
એક છોકરો, સુરેખ સમક્ષિતિજ રસ્તા પર તેના પર લાગતાં 5 N જેટલા ઘર્ષણબળ વિરુદ્ધ ચાલે છે. 1.5 km જેટલું અંતર કાપ્યા પછી તે 100 m ત્રિજ્યાવાળા વર્તુળપથ પર રસ્તો ભૂલી જાય છે. તે વર્તુળમાર્ગ પર 1.5 ચક્કર (cycle) લગાવ્યા બાદ આગળ તરફ વધારાનું 2.0 km અંતર ચાલે છે, તો છોકરા વડે થતું કાર્ય ગણો.

Hint: અત્રે, બળ F = 5 N
છોકરાનું કુલ સ્થાનાંતર,
s = 1.5 km + 200 m + 2 km
= 1500 m + 200 m + 2000 m
= 3700 m
હવે, કાર્ય % = (બળ F) (સ્થાનાંતર 3) સૂત્ર વાપરો.
ઉત્તર:
18500 J

પ્રશ્ન 15.
એક મોટર પમ્પનો પાવર 2 kW છે. 10 m જેટલી ઊંચાઈ સુધી 1 minute માં આ પમ્પ કેટલું પાણી ચઢાવી શકે? (g = 10 m s^-2)
Hint: પાવર P = \(\frac{W}{t}\) = \(\frac{m g h}{t}\)
∴ 2000 = \(\frac{m \times 10 \times 10}{60}\)
∴ m = 1200 kg
ઉત્તર:
m = 1200 kg

પ્રશ્ન 16.
એક ગ્રહ A પર એક માણસનું વજન, પૃથ્વી પરના તેના વજન કરતાં અડધું છે. તે પૃથ્વીની સપાટી પર 0.4 m ઊંચાઈનો કૂદકો લગાવી શકે છે, તો ગ્રહ A પર કેટલી ઊંચાઈનો કૂદકો લગાવી શકશે?
Hint: માણસની ગુરુત્વીય સ્થિતિ-ઊર્જા ગ્રહ A ઉપર અને પૃથ્વી
પર સમાન હશે.
∴ (mg₁h₁)_{પૃથ્વી}; = (mg₂h₂) A
∴ (mg₁) h₁ = \(\left(\frac{m g_{1}}{2}\right)\)h₂
∴ h₂ = 2h₁
= 2 × 0.4 m
= 0.8m
ઉત્તર:
0.8 m

પ્રશ્ન 17.
એક બૉલ 10 m ઊંચાઈએથી મુક્ત પતન કરે છે. જમીન સાથે અથડાવવાથી તેની ઊર્જા 40 % ઘટી જાય છે, તો તે કેટલી ઊંચાઈ સુધી ઉછળી શકશે?
Hint: 10 m ઊંચાઈએ બૉલની સ્થિતિ-ઊર્જા
= mgh
= m × 10 × 10
= (100 m) J
જમીનને અથડાવવાથી 40 % ઊર્જા ઘટે છે. તેથી બૉલ પાસે બાકી રહેતી ઊર્જા = 60 % (100 m) J
= \(\frac{60}{100}\) (100 m)J
= (60 m) J
ધારો કે, બૉલ જમીન સાથેની અથડામણ બાદ, જમીનથી h’ ઊંચાઈ સુધી ઉછળી શકે છે, તો
60 m = m × 9 × h’
∴ 60 = 10 × h’
∴ h’ = 6 m
ઉત્તર:
6 m

પ્રશ્ન 18.
એક ઇલેક્ટ્રિક સ્ત્રીનો પાવર 1200 છે. તેનો વપરાશ દરરોજ 30 minute છે, તો કોઈ પણ વર્ષના એપ્રિલ મહિનામાં કુલ કેટલી વિદ્યુત-ઊર્જા વપરાઈ હશે?
Hint: P = 1200 W = 1.2 kw
t = 30 minute = 0.5 h
કુલ વિદ્યુત-ઊર્જા,
E = પાવર × સમય × એપ્રિલ મહિનાના દિવસો
= 1.2 × 0.5 × 30 = 18 kWh
ઉત્તર:
18 kWh

પ્રશ્ન 19.
એક હલકા અને બીજા ભારે પદાર્થના વેગમાન સમાન છે. તેમની ગતિ-ઊર્જાનો ગુણોત્તર શોધો. કોની ગતિ-ઊર્જા વધુ હશે?
Hint: ગતિ-ઊર્જા E_k = \(\frac{1}{2}\) mv²

ઉત્તર:
\(\frac{\left(E_{\mathrm{k}}\right)_{1}}{\left(E_{\mathrm{k}}\right)_{2}}\) = \(\frac{m_{2}}{m_{1}}\), હલકા પદાર્થની ગતિ-ઊર્જા વધુ

પ્રશ્ન 20.
એન્જિન ચાલુ હોવાને લીધે 1000 kg દળવાળી કાર A સમક્ષિતિજ સુરેખ રસ્તા પર 36 kWh^-1 જેટલી ઝડપે ગતિ કરે છે. જો તેની ગતિને અવરોધતું બળ 100 N હોય, તો તેના એન્જિનનો પાવર શોધો.

હવે, કાર A 200 m અંતર કાપ્યા પછી, તેટલું જ દળ ધરાવતી સ્થિર કાર B સાથે અથડાય છે અને સ્થિર થાય છે. પરિણામે કાર B તે સમક્ષિતિજ રસ્તા પર ગતિ કરવા લાગે છે, તો કાર Bની ઝડપ અથડામણ પછી તરત જ કેટલી હશે? (કાર થનું એન્જિન બંધ છે.)
Hint: દળ (m)_A = (m)_B = 1000 kg
ઘર્ષણબળ F = 100 N.
કાર A ના એન્જિનનો પાવર P = F_v
= 100 × 10 (∵ v = 10 m s^-1)
= 1000 W
વેગમાન સંરક્ષણનો નિયમ વાપરતાં,
m_Au_A + m_Bu_B = m_AV_A + m_Bv_B
(1000 × 10) + (1000 × 0) = (1000 × 2) + (1000 × v_B)
∴ v_B = 10 m s^-1
ઉત્તર:
1000 W, 10 m s^-1

પ્રશ્ન 21.
35 kg દળવાળી એક છોકરી 5 kg દળવાળી ટ્રૉલીમાં બેઠી છે. ટ્રૉલી પર બળ લગાડીને તેને 4 m s^-1 જેટલો વેગ આપવામાં આવે છે. ટ્રોલી 16 m જેટલું અંતર કાપ્યા બાદ સ્થિર થાય છે, તો
(1) ટ્રૉલી પર કેટલું કાર્ય થયું હશે?
ઉત્તર:
320 J

(2) છોકરી પર કેટલું કાર્ય થયું હશે?
ઉત્તર:
0

પ્રશ્ન 22.
ચાર માણસો ભેગા મળીને 250 kg દળનું બૉક્સ 1 m ઊંચાઈ સુધી ઊંચકે છે. બૉક્સને ઊંચે કે નીચે લઈ ગયા વગર તેઓ તેને પકડી રાખે છે. (g = 10 m s^-2)
(1) બૉક્સને ઊંચકવા માટે માણસો દ્વારા કેટલું કાર્ય થયું હશે?
ઉત્તર:
2500 J

(2) બૉક્સને તે ઊંચાઈએ પકડી રાખવા માટે તેમણે કેટલું કાર્ય કરવું પડે?
ઉત્તર:
0

(3) બૉક્સને પકડી રાખવાના લીધે તેઓ શા માટે થાકી જાય છે?
ઉત્તર:
બૉક્સને પકડી રાખવા માટે માણસોએ બૉક્સ પર લાગતાં ગુરુત્વાકર્ષણ બળ વિરુદ્ધ કાર્ય તેમની સ્નાયુ-શક્તિ વડે કરવું પડે. તેથી તેઓ થાકી જાય છે.

પ્રશ્ન 23.
કર્ણાટક રાજ્યમાં આવેલ ‘જોગ’ નામના જલધોધની ઊંચાઈ 20 m છે. તેમાંથી 1 મિનિટમાં 2000 ટન પાણી નીચે પડે છે. જો આ સમગ્ર ઊર્જા વપરાય, તો તેને અનુરૂપ પાવર શોધો. (g = 10 m s^-2)
Hint: પાવર P = \(\frac{W}{t}\) = \(\frac{m g h}{t}\)
= \(\frac{2 \times 10^{6} \times 10 \times 20}{60}\)
= \(\frac{2}{3}\) × 10 w
ઉત્તર:
\(\frac{2}{3}\) × 10⁷ w

પ્રશ્ન 24.
એક માણસ 100 % જેટલા અચળ દરે કાર્ય કરે છે. 1 m s^-1 જેટલા અચળ વેગથી તે કેટલું દળ ઉપર તરફ ઊંચકી શકે? (g = 10 m s^-2).
Hint: પાવર P = \(\frac{W}{t}\) = \(\frac{m g h}{t}\) = mg \(\left(\frac{h}{t}\right)\) = mgv
∴ m = \(\frac{P}{g v}\) = \(\frac{100}{10 \times 1}\) = 10 kg
ઉત્તર:
10 kg

પ્રશ્ન 25.
150 kg દળવાળું કાર-એન્જિન 1 kg દળ માટે 500 W પાવર ખર્ચે છે. કારને 20 m s^-1 જેટલી અચળ ઝડપે ગતિ કરાવવા માટે એન્જિન વડે કેટલું બળ લાગવું જોઈએ?
Hint: કુલ પાવર = 150 × 500 = 7.5 × 10⁴w

ઉત્તર:
3750 N

પ્રશ્ન 26.
1.0 g દળવાળું એક પતંગિયું ગુરુત્વાકર્ષણ બળ વિરુદ્ધ 0.5 m s^-1ના વેગથી ઊર્ધ્વગતિ કરે છે અને એક 250 g દળવાળી ખિસકોલી ઝાડ પર 0.5 m s^-1ના વેગથી ઉપર ચઢે છે, તો તેમના પાવરની સરખામણી કરો. (g = 10 m s^-2).
Hint: પતંગિયાનો પાવર P = Fv
= (mg)v
= (10^-3 kg) × (10 m s^-2) (0.5 m s^-1)
= 5 × 10^-3W

ખિસકોલીનો પાવર P’ = F’v’.
= (m’g)v’
= (250 × 10^-3kg) × (10 ms^-2) × (0.5 m s^-1)
= 1.25 w
∴ ખિસકોલીનો પાવર > પતંગિયાનો પાવર
ઉત્તર:
ખિસકોલીનો પાવર પતંગિયા કરતાં વધુ છે.

પ્રશ્ન 27.
નીચેની આકૃતિમાં એક સાદું લોલક દર્શાવ્યું છે, જેના ગોળાનું દળ 100 g છે. પ્રારંભમાં ગોળો સમતોલન સ્થાન ‘O’ પાસે ? સ્થિર અવસ્થામાં છે. તેને એક બાજુ તરફ A બિંદુએ સ્થાનાંતરિત કરવામાં આવે છે. A સ્થાનની 2 બિંદુથી ઊંચાઈ 5 cm છે.

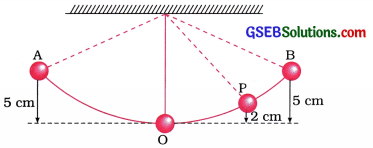
(1) ગોળાની A સ્થાને સ્થિતિ-ઊર્જા શોધો.
(2) P બિંદુએ ગોળાની ગતિ-ઊર્જા શોધો.
P બિંદુ, 2 બિંદુથી 2 cm ઊંચાઈએ છે. 9 = 10 m s^-2)

Hint: (1) E_p = mgh = 0.1 × 10 × 0.05 = 0.05 J
(2) E_k = \(\frac{1}{2}\) mv²
પણ સાદા લોલકનો ગોળો મુક્તપણે દોલનો કરે છે.
v² – 0² = 2gs ⇒ v² = 2gh
∴ E_k = \(\frac{1}{2}\)m (2gh) = mgh
= 0.1 × 10 × 0.02
= 0.02 J
ઉત્તર:
(1) 0.05 J
(2) 0.02 J

પ્રશ્ન 28.
એક કારનું દળ 1000 kg છે. તે 15 m s^-1ની ઝડપે ગતિ કરે છે. તેને બ્રેક લગાડવાને લીધે તે 25 m અંતર કાપીને સ્થિર થાય છે. બ્રેક દ્વારા લગાડેલ બળ શોધો અને બ્રેક-બળ દ્વારા થતું કાર્ય શોધો.
Hint: v² – u² = 2as
⇒ 0² – (15)² = 2a × 25
∴ a = – 4.5 m
બ્રેક દ્વારા લાગતું બળ F = ma
= 1000 × – 4.5)
= – 4500 N
|F| = 4500 N
બ્રેક-બળ દ્વારા થતું કાર્ય W = Fs
= – 4500 × 25
= – 112500 J
ઉત્તર:
4500 N, – 112500 J

પ્રશ્ન 29.
5 m s^-2ના પ્રવેગથી ગતિ કરતો 25 kg દળવાળો પદાર્થ 4 m અંતર કાપે તે દરમિયાન થયેલ કાર્ય શોધો.
ઉત્તર:
500 J

પ્રશ્ન 30.
10 kg દળવાળા પદાર્થને h મીટર ઊંચાઈએ ઊંચકવા કરવું પડતું કાર્ય 500 J હોય, તો hનું મૂલ્ય શોધો. (g = 10 m s^-2 લો.)
ઉત્તર:
h = 5 m

પ્રશ્ન 31.
0.01 km ઊંચાઈએથી પડતો 1000 g દળવાળો પદાર્થ જમીન પર આવે ત્યારે તેની ગતિ-ઊર્જા કેટલી હોય? (g =10 m s^-2 લો.)
ઉત્તર:
100 J

પ્રશ્ન 32.
60 kg દળવાળી એક વ્યક્તિ માથા પર 40 kgનો બોજ ઊંચકીને 1 મિનિટમાં 15 m ઊંચે જતી હોય, તો વ્યક્તિથી થયેલું કાર્ય અને પાવર શોધો. (g = 10 m s^-2 લો.)
ઉત્તર:
W = 1.5 × 10⁴J; P = 250 w

પ્રશ્ન 33.
60 kg દળવાળી એક વ્યક્તિ માથા પર 20 kgનો બોજ ઊંચકીને દાદરનાં 20 પગથિયાં 10 sમાં ચઢે છે. જો પ્રત્યેક પગથિયાની ઊંચાઈ 0.2 m હોય, તો વ્યક્તિનો પાવર શોધો,
ઉત્તર:
320 W

પ્રશ્ન 34.
100 W નો બલ્બ દરરોજ 2 કલાક અને 40 Wની પાંચ ટ્યૂબલાઇટ દરરોજ 4 કલાક ચાલુ રાખવામાં આવે, તો જૂન મહિનામાં કેટલા યુનિટ વિદ્યુત-ઊર્જા વપરાય?
ઉત્તર:
30 unit

પ્રશ્ન 35.
1500 kg દળ ધરાવતી કારની ઝડપ 54 km h^-1થી વધીને 72 km h^-1 થાય છે. આ ઝડપ વધારવા માટે કરવું પડતું કાર્ય
ગણો.
ઉત્તર:
131250 J

પ્રશ્ન 36.
0.5 hpનો પાવર ધરાવતી મોટર દ્વારા 5 m ઊંચાઈએ 98 sમાં કેટલા કિલોગ્રામ પાણી ચઢશે?
ઉત્તર:
746 kg

નીચેનાં પદો કે રાશિઓ વચ્ચે તફાવત આપો

પ્રશ્ન 1.
કાર્ય અને ઊર્જા
ઉત્તર:

કાર્ય	ઊર્જા
1. સામાન્ય રીતે પદાર્થ પર બળ લાગતાં પદાર્થનું સ્થાનાંતર બળની દિશામાં થાય ત્યારે કાર્ય થયું કહેવાય.	1. પદાર્થમાં રહેલી કાર્ય કરવાની ક્ષમતાને ઊર્જા કહે છે.
2. કાર્ય એ ઊર્જાની અસર છે.	2. ઊર્જા એ કાર્યનું કારણ છે.

પ્રશ્ન 2.
સ્થિતિ-ઊર્જા અને ગતિ-ઊર્જા
ઉત્તર:

સ્થિતિ-ઊર્જા	ગતિ-ઊર્જા
1. પદાર્થની સંરચના અને અથવા સ્થાનના કારણે પદાર્થ કાર્ય કરવાની જે ક્ષમતા ધરાવે છે, તેને પદાર્થની સ્થિતિ-ઊર્જા કહે છે.	1. પદાર્થ પોતાની ગતિને કારણે કાર્ય કરવાની જે ક્ષમતા ધરાવે છે, તેને ગતિ-ઊર્જા કહે છે.
2. પૃથ્વીની સપાટીએ સ્થિતિ-ઊર્જા શૂન્ય માનતાં કે જેટલી ઊંચાઈએ, Ep = mgh સૂત્ર વડે પદાર્થની (ગુરુત્વીય) સ્થિતિ-ઊર્જાનું મૂલ્ય નક્કી કરી શકાય	2. E<sub>k</sub> = \(\frac{1}{2}\) mv2 સૂત્રની મદદથી પદાર્થની ગતિ-ઊર્જાનું મૂલ્ય નક્કી કરી શકાય.

પ્રશ્ન 3.
ઊર્જા અને પાવર
ઉત્તર:

ઊર્જા	પાવર
1. પદાર્થમાં રહેલી કાર્ય કરવાની ક્ષમતાને ઊર્જા કહે છે.	1. પદાર્થના કાર્ય કરવાના દરને પાવર કહે છે.
2. ઊર્જાનો એકમ જૂલ (J) છે.	2. પાવરનો એકમ જૂલ સેકન્ડ (U/s) અથવા વૉટ (W) છે.

પ્રશ્ન 4.
કાર્ય અને કાર્યત્વરા
ઉત્તર:

કાર્ય	કાર્યવાહી
1. સામાન્ય સંજોગોમાં પદાર્થ પર બળ લાગતાં તેનું સ્થાનાંતર બળની દિશામાં થાય, તો બળ અને સ્થાનાંતરના ગુણનફળને કાર્ય કહે છે.	1. કાર્ય કરવાના દરને કાર્યત્વરા કહે છે.
2. વ્યાપક રીતે કાર્ય W = F1s જ્યાં, F1 = અસરકારક બળ અને s = સ્થાનાંતર	2. કાર્યત્વરા P = \(\frac{W}{t}\) જ્યાં, W = કાર્ય અને t = સમય
3. કાર્યનાં મૂલ્યનો આધાર સમય t પર નથી.	3. કાર્યત્વરાના મૂલ્યનો આધાર સમય પર છે.
4. કાર્યનો SI એકમ જૂલ (J) છે.	4. કાર્યત્વરાનો SI એકમ જૂલ/સેકન્ડ (J s-1) છે.

નીચેના વિધાનોનાં વૈજ્ઞાનિક કારણો આપોઃ

પ્રશ્ન 1.
માથા પર બોજ ઊંચકીને ઊભેલો માણસ કે તેને લઈને ચાલતો માણસ વૈજ્ઞાનિક દષ્ટિએ કંઈ જ કાર્ય કરતો નથી.
ઉત્તર:
કારણ કે માથા પર બોજ ઊંચકીને ઊભેલો માણસ બોજ પર ઊર્ધ્વદિશામાં બળ લગાવે છે, પણ બળની દિશામાં (ઊર્ધ્વદિશામાં) તે બોજનું સ્થાનાંતર થતું નથી. તેથી W = Fs = F × 0 = 0 પરથી બોજ પર થયેલું કાર્ય શૂન્ય ગણાય. તેથી કહી શકાય કે બોજ ઊંચકીને ઊભેલો માણસ કંઈ જ કાર્ય કરતો નથી.

હવે, જો બોજ લઈને માણસ ચાલતો હોય તો પણ માણસ બોજ પર કંઈ જ કાર્ય કરતો નથી. તેનું કારણ માણસ બોજ પર ઊર્ધ્વદિશામાં બળ લગાડતો હોય છે, જ્યારે તેની ગતિ સમક્ષિતિજ દિશામાં હોવાથી તેનું સ્થાનાંતર સમક્ષિતિજ દિશામાં છે. તેથી બળ અને સ્થાનાંતર વચ્ચેનો ખૂણો 90° હોવાથી W = F × s = 0 × s = 0 પરથી બોજ પર કંઈ જ કાર્ય થતું નથી.

પ્રશ્ન 2.
બંદૂકમાંથી છૂટેલી ગોળી (bullet) જાડા લાકડાના પાટિયામાં ઘૂસી શકે છે. પણ હાથના ઘા વડે ફેકેલી તે જ ગોળી પાટિયામાં ઘૂસી શકતી નથી.
ઉત્તર:
કારણ કે બંદૂકમાંથી છૂટેલી ગોળીનો વેગ છે પ્રચંડ હોવાથી E_k ∝ v² (∵ m = અચળ) અનુસાર ગોળીની ગતિ-ઊર્જા E ખૂબ જ વધુ હોવાથી તે પાટિયાની અંદર ઘૂસી શકે છે.

જ્યારે હાથના ઘા વડે ફેકેલી ગોળીનો વેગ v ઓછો હોવાથી E_k ∝ v² મુજબ તેની ગતિ-ઊર્જા E_k ઓછી હોય છે. પરિણામે તે પાટિયાની અંદર ઘૂસી શકતી નથી.

પ્રશ્ન 3.
પૃથ્વી સૂર્યની આસપાસ ભ્રમણ કરે છે ત્યારે સૂર્યના ગુરુત્વાકર્ષણ બળથી થયેલું કાર્ય શૂન્ય હોય છે.
ઉત્તર:
કારણ કે પૃથ્વી સૂર્યની આસપાસ ભ્રમણ કરે છે ત્યારે પૃથ્વી પર લાગતું સૂર્યનું ગુરુત્વાકર્ષણ બળ કક્ષાના કેન્દ્ર તરફ હોય છે અને પૃથ્વીનું સ્થાનાંતર વર્તુળમય કક્ષાના સ્પર્શકની દિશામાં હોય છે. આમ, પૃથ્વીનું સ્થાનાંતર સૂર્યના ગુરુત્વાકર્ષણ બળની લંબ દિશામાં છે. પદાર્થનું સ્થાનાંતર બળની લંબ દિશામાં થાય તો થયેલું કાર્ય W = F × s = 0 × 9 = 0 હોય. તેથી પૃથ્વી સૂર્યની આસપાસ ભ્રમણ કરે છે ત્યારે સૂર્યના ગુરુત્વાકર્ષણ બળથી થયેલું કાર્ય શૂન્ય હોય છે.

પ્રશ્ન 4.
લાકડામાં ખીલી ઠોકતી વખતે ખીલીના માથા પર અફાળવાની હથોડી પાછળ તરફ ઊંચકી આગળ લાવવામાં આવે છે.
ઉત્તર:
કારણ કે પાછળ તરફ ઊંચકેલી હથોડી ઝડપથી આગળ લાવતાં તેના વેગમાં વધારો થાય છે અને હથોડી વધુ ગતિ-ઊર્જા ધરાવે છે. હથોડીની વધુ ગતિ-ઊર્જાને કારણે વધુ કાર્ય મેળવી શકાય છે. તેથી હથોડી વડે ખીલી લાકડામાં સરળતાથી ઠોકી શકાય છે.

પ્રશ્ન 5.
ઘડિયાળ ચાલુ રાખવા માટે સમય-સમય પર એની સ્પ્રિંગ વીંટાળવી જરૂરી છે.
ઉત્તર:
કારણ કે વીંટાળેલી સ્પ્રિંગમાં તેની સંરચનાને લીધે તેમાં (સ્થિતિસ્થાપકીય) સ્થિતિ-ઊર્જાનો સંગ્રહ થાય છે. સ્પ્રિંગ ઉકેલાતાં સ્થિતિ-ઊર્જાનું રૂપાંતર ગતિ-ઊર્જામાં થાય છે અને ઘડિયાળનાં ચક્રો ગતિમાન થાય છે. સ્પ્રિંગ સંપૂર્ણ ઊલ્લી જતાં સ્થિતિ-ઊર્જા શૂન્ય થાય છે. ઘડિયાળનાં ચક્રો સતત ચાલુ રાખવા માટે સ્પ્રિંગ ફરી વીંટાળી ઊર્જાનો સંગ્રહ કરવો પડે છે.

પ્રશ્ન 6.
પૃથ્વીની સપાટીથી કે જેટલી ઊંચાઈએથી કોઈ પદાર્થ મુક્ત પતન કરે છે ત્યારે તેની ગુરુત્વીય સ્થિતિ-ઊર્જા ક્રમિક રીતે ઘટતી જાય છે, પણ તેની યાંત્રિક ઊર્જા બદલાતી નથી.
ઉત્તરઃ
કારણ કે પૃથ્વીની સપાટીથી ૧ જેટલી ઊંચાઈએ પદાર્થની ગુરુત્વીય સ્થિતિ-ઊર્જા mgh જેટલી હોય છે. હવે જ્યારે પદાર્થ મુક્ત પતન શરૂ કરે છે ત્યારે પૃથ્વીની સપાટીથી તેની ઊંચાઈ h ક્રમિક રીતે ઘટે છે. તેથી તેની ગુરુત્વીય સ્થિતિ-ઊર્જા ઘટવા લાગે છે.

પરંતુ, મુક્ત પતન કરતો પદાર્થ અધોદિશામાં અચળ પ્રવેગી (a = g) ગતિ કરતો હોવાથી તેના વેગમાં નિયમિત વધારો થતો હોવાથી E_k = \(\frac{1}{2}\)mv² સૂત્ર પરથી તેની ગતિ-ઊર્જા વધતી જાય છે.

હવે યાંત્રિક ઊર્જા સંરક્ષણના નિયમ, Δ E_k = – Δ E_p પરથી સ્થિતિ-ઊર્જા જેટલા પ્રમાણમાં ઘટે છે તેટલા જ પ્રમાણમાં ગતિ-ઊર્જા વધતી હોય છે. તેથી E = E_p + E_k સૂત્ર પરથી પદાર્થની યાંત્રિક ઊર્જા બદલાતી નથી.

જોડકાં જોડો:

પ્રશ્ન 1.

વિભાગ I	વિભાગ II
1. કાર્યનો એકમ	a. ગતિ-ઊર્જા
2. પાવરનો એકમ	b. સ્થિતિ-ઊર્જા
3. દબાયેલી સ્પ્રિંગમાં રહેલી ઊર્જા	c. ન્યૂટન
4. બંદૂકમાંથી છૂટેલી ગોળીમાં રહેલી. ઊર્જા	d. જૂલ
	e. જૂલ સેકન્ડ

ઉત્તર:

વિભાગ I	વિભાગ II
1. કાર્યનો એકમ	d. જૂલ
2. પાવરનો એકમ	e. જૂલ સેકન્ડ
3. દબાયેલી સ્પ્રિંગમાં રહેલી ઊર્જા	b. સ્થિતિ-ઊર્જા
4. બંદૂકમાંથી છૂટેલી ગોળીમાં રહેલી. ઊર્જા	a. ગતિ-ઊર્જા

પ્રશ્ન 2.

વિભાગ I (ભૌતિક રાશિ)	વિભાગ II (સૂત્ર)
1. કાર્ય	a. \(\frac{W}{t}\)
2. પાવર	b. mgh
3. સ્થિતિ-ઊર્જા	c. \(\frac{1}{2}\)mv2
4. ગતિ-ઊર્જા	d. Fs
	e. ma

ઉત્તર:

વિભાગ I (ભૌતિક રાશિ)	વિભાગ II (સૂત્ર)
1. કાર્ય	d. Fs
2. પાવર	a. \(\frac{W}{t}\)
3. સ્થિતિ-ઊર્જા	b. mgh
4. ગતિ-ઊર્જા	c. \(\frac{1}{2}\)mv2

પ્રસ્તાવના

પ્રશ્ન 1.
રોજિંદા જીવનમાં કાર્યનો અર્થ શું છે?
ઉત્તરઃ
જુદી જુદી પ્રવૃત્તિઓ (Activities) કરવા માટે આપણને (સજીવોને) ખોરાકની જરૂર પડે છે. ખોરાક આ પ્રવૃત્તિઓ કરવા માટે આપણને ઊર્જા પૂરી પાડે છે.
જીવિત રહેવા માટે દરેક સજીવને અનેક મૂળભૂત ગતિવિધિઓ અને શારીરિક કામો કરવા પડે છે. આ મૂળભૂત ગતિવિધિ પ્રવૃત્તિઓ)ને જૈવિક પ્રક્રિયા કહે છે.

કેટલાંક કાય જેમ કે, રમવું, ગાવું, ભણવું, લખવું, વિચારવું, કૂદવું, દોડવું તથા સાઇકલ ચલાવવી વગેરે માટે આપણને ઊર્જાની જરૂર પડે છે. પ્રાણીઓને પણ દોડવું, કૂવું, લડવું, પોતાના દુશ્મનોથી દૂર ભાગવું વગેરે માટે ઊર્જાની જરૂર પડે છે. રોજિંદા જીવનમાં થતી ઉપરોક્ત વિવિધ પ્રવૃત્તિ(કામ)ને કાર્ય કહે છે.
રોજિંદા જીવનમાં કાર્ય શબ્દનો અર્થ અને વિજ્ઞાનમાં “કામ” શબ્દનો અર્થ તદ્દન ભિન્ન છે.

પ્રશ્ન 2.
વિજ્ઞાનની પરિભાષાના આધારે નીચેનું વિધાન સમજાવોઃ “સખત મહેનત કરવા છતાં વધુ કાર્ય થતું નથી.”
ઉત્તરઃ
1. એક વિદ્યાર્થી વાર્ષિક પરીક્ષાની તૈયારી કરી રહ્યો છે. તે અધ્યયન કરવામાં ઘણો બધો સમય વાપરે છે. – તે પુસ્તકો વાંચે છે, ચિત્ર બનાવે છે, પોતાના વિચારોને વ્યવસ્થિત ક્રમબદ્ધ કરે છે, પ્રશ્નપત્રો એકઠાં કરે છે, વર્ગખંડમાં હાજર રહે છે, પોતાના મિત્રો સાથે સમસ્યાઓ પર વિચાર-વિમર્શ કરે છે તથા તે પ્રયોગો પણ કરે છે. ઉપરોક્ત પ્રક્રિયાઓમાં ઘણી બધી ઊર્જા વપરાય છે.
અહીં વિદ્યાર્થી સખત મહેનત કરી રહ્યો છે પણ વૈજ્ઞાનિક પરિભાષા અનુસાર આ સખત મહેનતમાં ખૂબ જ ઓછું કાર્ય સમાવિષ્ટ છે.

2. બીજો વિદ્યાર્થી બહુ જ મોટા પથ્થરને ધક્કો મારીને ખસેડવાનો પ્રયત્ન કરે છે, પણ પથ્થર બિલકુલ ખસતો નથી. વિદ્યાર્થી પૂરેપૂરો થાકી જાય છે, પણ વિજ્ઞાનની પરિભાષામાં તે વિદ્યાર્થીએ પથ્થર પર કોઈ કાર્ય કર્યું નથી. કેમ કે, પથ્થરનું સ્થાનાંતર થતું જ નથી.

3. ત્રીજો વિદ્યાર્થી પોતાના માથા પર એક ભારે વજન મૂકીને થોડીક મિનિટો સુધી ઊભો રહે છે. તે કંટાળી જાય છે, થાકી જાય 3 છે તથા તે પોતાની ઘણી બધી શક્તિ વાપરી નાખે છે. અહીં પણ વિજ્ઞાનમાં જે પ્રકારે કાર્ય શબ્દનો અર્થ છે, તે અર્થમાં આ પરિસ્થિતિમાં કાર્ય થયું નથી.

આમ, ઉપરોક્ત ઉદાહરણો દ્વારા સ્પષ્ટ થાય છે કે, “સખત મહેનત કરવા છતાં વધુ કાર્ય થતું નથી.
ટૂંકમાં, કાર્ય શું છે તે એ વાત ઉપર આધારિત છે કે, તેને કેવી 3 રીતે વર્ણવવામાં આવે છે. રોજિંદા જીવનમાં થતું કાર્ય અને વૈજ્ઞાનિક કાર્ય તદન ભિન્ન છે.

પ્રશ્ન 3.
પદાર્થ પર કાર્ય ક્યારે થયું ગણાય? સમજાવો.
અથવા
ભૌતિક વિજ્ઞાનની દષ્ટિએ પદાર્થ પર કાર્ય થયું છે તેવું ક્યારે 3 કહેવાય? કાર્યનું મૂલ્ય શાના પર આધાર રાખે છે?
ઉત્તરઃ
નીચેનાં ઉદાહરણો પરથી સ્પષ્ટ થાય છે કે પદાર્થ પર 3 કાર્ય થયું છેઃ

1. કોઈ સપાટી પર રાખેલા લીસા કાંકરા(Pebble)ને ધક્કો મારતાં (Push કરતાં) તે સપાટી પર થોડુંક અંતર કાપે છે.
અહીં કાંકરા પર બળ લાગ્યું, જેનાથી કાંકરો થોડોક સ્થાનાંતરિત થયો. આ સ્થિતિમાં કાર્ય થયું તેમ કહેવાય.

2. એક છોકરી, કોઈ ટ્રૉલીને ખેંચે છે અને ટ્રૉલી થોડું અંતર કાપે છે.
છોકરીએ ટ્રૉલી પર બળ લગાવ્યું અને તેનું સ્થાનાંતર થયું, એટલે કાર્ય થયું.

3. એક વિદ્યાર્થી પુસ્તકને થોડે ઊંચે સુધી ઉપાડે છે. આવું કરવા માટે તે બળ લગાડે છે, પુસ્તક ઊંચું થાય છે.
અત્રે પુસ્તક ઉપર બળ લાગ્યું અને પુસ્તક ગતિમાન થયું એટલે કાર્ય થયું તેમ કહેવાય.

ઉપરનાં ઉદાહરણોને ધ્યાનપૂર્વક જોતાં સ્પષ્ટ થાય છે કે, કાર્ય થવા માટે બે શરતોનું પાલન થવું જોઈએ:
(1) પદાર્થ પર કંઈક બળ લાગવું જોઈએ.
(2) પદાર્થનું સ્થાનાંતર થવું જોઈએ.

પ્રશ્ન 4.
એક બળદ કોઈ ગાડાને ખેંચી રહ્યો છે. ગાડું ગતિ કરે છે. ગાડા પર બળ લાગી રહ્યું છે અને ગાડું થોડું અંતર કાપે છે. શું તમારા મતે આ સ્થિતિમાં કાર્ય થઈ રહ્યું છે?
હા.

પ્રશ્ન 5.
એક પરિમાણમાં અચળ બળ વડે થતા કાર્યનું સૂત્ર મેળવો.
અથવા
કાર્ય એટલે શું? યોગ્ય આકૃતિ દોરીને તેની સમજૂતી આપો.
ઉત્તરઃ
પદાર્થ પર લાગતા બળના મૂલ્ય અને બળ જે સમયગાળા દરમિયાન લાગતું હોય તે સમયગાળા દરમિયાન બળની દિશામાં પદાર્થના થયેલા સ્થાનાંતરના મૂલ્યના ગુણનફળને પદાર્થ પર થતું કાર્ય કહે છે.

[આકૃતિ 11.1: પદાર્થ પર થતું કાર્ય]

→ આકૃતિ 11.1 માં દર્શાવ્યા મુજબ એક પદાર્થ પર અચળ બળ F લાગતાં પદાર્થનું બળની દિશામાં સ્થાનાંતર s જેટલું થાય છે, તો આ દરમિયાન થતા કાર્યનું મૂલ્ય નીચેના સૂત્ર પરથી મળે છે:
કાર્ય કાર્ય = બળ × બળની દિશામાં (બળ લાગતું હોય તે સમયગાળા દરમિયાન) થતું સ્થાનાંતર
આમ, W = Fs .. … (11.1)

→ બળ અને સ્થાનાંતર બંને સદિશ રાશિ છે, પરંતુ કાર્ય અદિશ રાશિ છે.

→ સમીકરણ (11.1) પરથી સ્પષ્ટ છે કે પદાર્થ પર લાગતું બળ F શૂન્ય હોય, તો કરેલું કાર્ય W = 0 હોય છે અને જો પદાર્થ પર બળ લાગે પણ સ્થાનાંતર = શૂન્ય હોય, તોપણ કાર્ય W = 0 હોય છે.

પ્રશ્ન 6.
SI એકમ પદ્ધતિમાં કાર્યનો એકમ મેળવો અને તેની વ્યાખ્યા લખો.
ઉત્તર:
કાર્ય W = Fs
→ SI એકમ પદ્ધતિમાં બળનો એકમ ન્યૂટન (N) અને સ્થાનાંતરનો એકમ મીટર (m) છે. તેથી કાર્યનો એકમ ન્યૂટન-મીટર (N m) થાય.

→ ભૌતિક વૈજ્ઞાનિક જૂલની યાદમાં આ એકમને જૂલ (0) કહે છે. આમ, 1 = 1 N m
જૂલ (J) ની વ્યાખ્યા: પદાર્થ પર 1 N બળ લાગતાં પદાર્થનું સ્થાનાંતર બળની દિશામાં 1 m જેટલું થતું હોય, તો તેના પર થયેલું કાર્ય 1 J કહેવાય છે.

પ્રશ્ન 7.
પદાર્થ પર અચળ બળ ર લાગે છે, તો કઈ પરિસ્થિતિમાં તે બળ વડે થયેલું કાર્ય (1) ધન અને (2) ઋણ હશે?
ઉત્તર:
1. જો પદાર્થ પર લાગતા બળ ‘F’ અને પદાર્થના સ્થાનાંતર ‘s’ની દિશા એક જ હોય, તો તે બળ વડે થયેલું કાર્ય ‘W’ ધન હોય છે.
દા. ત., એક બાળકી જમીન પર રહેલી રમકડાની કારને દોરી વડે જમીનને સમાંતર ખેંચે છે. અહીં કારના સ્થાનાંતરની દિશા અને કાર પર લાગતા બળની દિશા એક જ છે. આ પરિસ્થિતિમાં બાળકી વડે લગાડેલા બળને લીધે થયેલું કાર્ય ધન ગણાય.

2. જો કોઈ પદાર્થ પર ઘણાં બધાં બળો લાગતાં હોય અને તેમાંથી કોઈ એક બળ ‘F’ સ્થાનાંતર ‘s’ની વિરુદ્ધ લાગી રહ્યું છે. એટલે કે તે બળ F અને સ્થાનાંતર = વચ્ચેનો ખૂણો 180° છે, તો આવી પરિસ્થિતિમાં તે બળ F વડે થયેલું કાર્ય ઋણ ગણાય.
દા. ત., જ્યારે કોઈ પદાર્થને શિરોલંબ ઊર્ધ્વદિશામાં ફેંકવામાં આવે છે ત્યારે તેના સ્થાનાંતર (s)ની દિશા ઊર્ધ્વદિશા છે, પણ તેના પર લાગતા પૃથ્વીના ગુરુત્વાકર્ષણ બળ (mg)ની દિશા અધોદિશા છે. આવી પરિસ્થિતિમાં ગુરુત્વાકર્ષણ બળ વડે ઊર્ધ્વદિશામાં ગતિ કરતા પદાર્થ પર થયેલું કાર્ય કણ ગણાય.

પ્રશ્ન 8.
પદાર્થ પર બળ લાગતાં તેનું
(1) સ્થાનાંતર ન થાય
ઉત્તર:
1. સમક્ષિતિજ સપાટી પર રહેલા મોટા પથ્થરને એક વ્યક્તિ બળ લગાડીને તેને ખસેડવાનો પ્રયત્ન કરે છે, પણ | પથ્થર ખસતો નથી, એટલે કે તેનું સ્થાનાંતર થતું નથી. આવી પરિસ્થિતિમાં થતું કાર્ય W = F × 0 = 0 છે.

(2) સ્થાનાંતર બળની દિશામાં થાય
ઉત્તર:

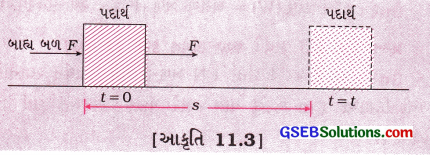
[આકૃતિ 11.3]

આકૃતિ 11.3માં દર્શાવ્યા મુજબ સમક્ષિતિજ સપાટી પર રહેલા પદાર્થ પર બાહ્ય બળ લાગતાં તેનું સ્થાનાંતર = જેટલું બળની દિશામાં થાય છે. તેથી અહીં થતું કાર્ય w = F × s જે બાહ્ય બળ વડે થાય છે. આ કાર્ય ધન હોય છે અને અહીં બળ અને સ્થાનાંતર એક જ દિશામાં છે.

(3) સ્થાનાંતર બળની વિરુદ્ધ દિશામાં થાય અને
ઉત્તર:

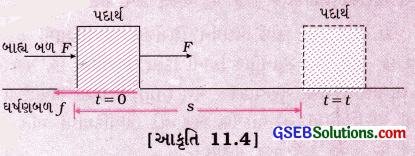
[આકૃતિ 11.4]

આકૃતિ 11.4માં દર્શાવ્યા મુજબ સમક્ષિતિજ સપાટી પર રહેલા પદાર્થનું સ્થાનાંતર s જેટલું, તેના પર લાગતાં ઘર્ષણબળ f વિરુદ્ધ થાય છે. તેથી અહીં થતું કાર્ય W = – f × s ઘર્ષણબળ વડે થાય છે. આ કાર્ય ઋણ હોય છે અને અહીં (ઘર્ષણ)બળ અને સ્થાનાંતર પરસ્પર વિરુદ્ધ દિશામાં છે.

(4) સ્થાનાંતર બળને લંબરૂપે થતું હોય, તો કાર્ય કેવી રીતે ગણવામાં આવે છે? ઉદાહરણ આપી સમજાવો.
ઉત્તર:

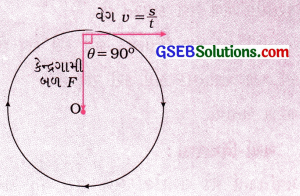
[આકૃતિ 11.55]

આકૃતિ 11.5માં દર્શાવ્યા મુજબ નિયમિત વર્તુળમય ગતિ કરતા પદાર્થ પર વર્તુળના કેન્દ્ર તરફ કેન્દ્રગામી બળ લાગે છે, પણ આ કેન્દ્રગામી બળને કારણે પદાર્થના વેગનું મૂલ્ય (ઝડપ) બદલાતું નથી. (અર્થાત્ u = v છે.)
એટલે કે અહીં પદાર્થની વર્તુળગતિ માટે કેન્દ્રગામી બળ વડે થતું કાર્ય શૂન્ય હોય છે.

પ્રશ્ન 9.
ઊર્જા એટલે શું? સમજાવો. ઊર્જાનો એકમ કાર્યના એકમ જેવો શાથી છે?
ઉત્તર:
પદાર્થમાં રહેલી કાર્ય કરવાની ક્ષમતાને પદાર્થની ઊર્જા કહે છે.
→ જે પદાર્થ પોતે કાર્ય કરે છે, તે ઊર્જા ગુમાવે છે અને જે પદાર્થ પર કાર્ય થાય છે તે ઊર્જા મેળવે છે.

→ ધારો કે, પદાર્થ A પાસે ઊર્જા છે, જ્યારે તે બીજા પદાર્થ B સાથે આંતરક્રિયા કરે છે ત્યારે પદાર્થ B થોડીક ઊર્જા મેળવીને સ્થાનાંતરિત થાય છે. આમ, પદાર્થ A થોડીક ઊર્જા ગુમાવે છે અને પદાર્થ B થોડીક ઊર્જા મેળવે છે, જે દર્શાવે છે કે જે પદાર્થમાં ઊર્જા છે તે કાર્ય કરી શકે છે.

→ ટૂંકમાં, પદાર્થમાં રહેલી ઊર્જા તેના કાર્ય કરવાની ક્ષમતાના રૂપમાં હું માપી શકાય છે. આથી ઊર્જાનો એકમ અને કાર્યનો એકમ એક જ છે.

→ ઊર્જાનો SI એકમ જૂલ () છે.
નોંધઃ ઊર્જાનો મોટો એકમ કિલોજૂલ (NJ) છે.
1 kJ = 1000 J

પ્રશ્ન 10.
“કાર્ય એક એવી પ્રક્રિયા છે કે જેમાં પદાર્થની ઊર્જામાં ફેરફાર થાય છે.” સમજાવો.
ઉત્તરઃ
જો પદાર્થ દ્વારા કાર્ય કરવામાં આવે, તો પદાર્થની ઊર્જામાં ઘટાડો થાય છે.
દા. ત., જમીન પરથી કોઈ પદાર્થને ઊર્ધ્વદિશામાં ફેંકવામાં આવે છે ત્યારે તે પદાર્થ પોતે મેળવેલ ઊર્જામાંથી, ઊર્જા ખર્ચીને – કાર્ય કરીને ઉપર તરફ ગતિ કરે છે. પણ તેના પર સતત ગુરુત્વાકર્ષણ બળ, તેની ગતિની વિરુદ્ધ દિશામાં નીચે તરફ લાગતું હોય છે, જે તેની ગતિનો વિરોધ કરે છે. તેથી તેની ઊર્જા ઘટતી જાય છે.

→ ગતિમાન વાહન પર બ્રેક લગાડતાં તેની ઊર્જા ઘટવા લાગે છે. તેથી તેની ઝડપ ઘટે છે.

→ જો પદાર્થ પર કાર્ય કરવામાં આવે, તો પદાર્થની ઊર્જામાં વધારો થાય છે.
દા. ત., જમીન પર સ્થિર પડેલા પદાર્થને ઊંચકીને ધારો કે 10 m જેટલી ઊંચાઈએ લઈ જવામાં આવે ત્યારે પદાર્થ પર કાર્ય થાય છે અને તેની ઊર્જામાં વધારો થાય છે. »

→ સાઈકલ-સવાર પૅડલ લગાવે છે ત્યારે સાઈકલ પર કાર્ય થાય છે. તેથી સાઈકલની ઊર્જામાં વધારો થાય છે. તેથી તેની ઝડપ વધે છે.

→ આમ, જ્યારે કાર્ય પદાર્થ દ્વારા થાય કે પદાર્થ પર થાય છે ત્યારે ખરેખર તો ઊર્જાની આપ-લે થાય છે. (ઊર્જાનો વિનિમય થાય છે.)

→ આમ, પદાર્થ ઊર્જા ધારણ કરી શકે છે કાર્ય નહિ, કારણ કે આ કાર્ય તો ઊર્જાના વિનિમય સાથે સંકળાયેલી એક પ્રક્રિયા છે.

પ્રશ્ન 11.
ઊર્જાના મુખ્ય પ્રકારો લખો.
ઉત્તર:
યાંત્રિક ઊર્જા, સ્થિતિ-ઊર્જા, ગતિ-ઊર્જા, ઉષ્મા-ઊર્જા, રાસાયણિક ઊર્જા, વિદ્યુત-ઊર્જા અને પ્રકાશ-ઊર્જા વગેરે ઊર્જાના મુખ્ય પ્રકારો છે.

પ્રશ્ન 12.
ટૂંક નોંધ લખો ગતિ-ઊર્જા
ઉત્તરઃ
કોઈ પણ ગતિમાન પદાર્થ કાર્ય કરી શકે છે. અર્થાત્ ગતિશીલ પદાર્થો ઊર્જા ધરાવતા હોય છે. આ ઊર્જાને ગતિ-ઊર્જા કહે છે.
પદાર્થ પોતાની ગતિને કારણે કાર્ય કરવાની જે ક્ષમતા ધરાવે છે એટલે કે ઊર્જા ધરાવે છે, તેને પદાર્થની ગતિ-ઊર્જા કહે છે.
ઝડપથી ગતિ કરતા પદાર્થ તેના જેવી જ પણ ધીમેથી ગતિ કરતા પદાર્થની સાપેક્ષમાં વધારે કાર્ય કરી શકે છે. બીજા શબ્દોમાં પદાર્થની ગતિ-ઊર્જા તેની ઝડપ સાથે વધે છે.

વ્યાખ્યાઃ કોઈ નિશ્ચિત વેગથી ગતિ કરતા પદાર્થની ગતિ-ઊર્જા પદાર્થને તે વેગ પ્રાપ્ત કરવા માટે કરવા પડતા કાર્ય બરાબર હોય છે.
→ ગતિ-ઊર્જાની સંજ્ઞા E_k છે.
→ ગતિ-ઊર્જાનો SI એકમ જૂલ (J) છે.
→ ગતિ-ઊર્જાનું મૂલ્ય નીચેની બે સહેલી રીતે શોધી શકાય છે:

1. v વેગથી ગતિ કરતા પદાર્થ પર ગતિ વિરુદ્ધ બળ લગાડતાં તે થોડા સમય બાદ સ્થિર થાય છે. આ સમયગાળા દરમિયાન થયેલા કાર્યની ગણતરી કરતાં ગતિ-ઊર્જા મેળવી શકાય છે.

2. સ્થિર સ્થિતિમાં રહેલા પદાર્થને ઇ વેગવાળી ગતિની અવસ્થામાં લાવવા માટે કરવા પડતા કાર્યની ગણતરી કરીને ગતિ-ઊર્જા મેળવી શકાય છે.

પ્રશ્ન 13.
પદાર્થની ગતિ-ઊર્જાનું સમીકરણ મેળવો.
ઉત્તર:
ધારો કે, m દળનો એક પદાર્થ પ જેટલા સમાન વેગથી ગતિ કરી રહ્યો છે.
→ હવે ધારો કે, તેના પર F જેટલું અચળ બળ સ્થાનાંતરની દિશામાં લાગે છે. તેથી t સમયમાં તે s જેટલું સ્થાનાંતર કરી છે જેટલો વેગ પ્રાપ્ત કરે છે.

→ આ પ્રક્રિયા દરમિયાન થતું કાર્ય % હોય, તો
W = Fs
પણ ન્યૂટનના ગતિના બીજા નિયમ અનુસાર, F = ma
∴ W = (ma) s ….. (11.2)

→ અચળ પ્રવેગી ગતિના સમીકરણ v² – u² = 2as પરથી,
s = \(\frac{v^{2}-u^{2}}{2 a}\) ……… (11.3)

→ સમીકરણ (11.3)ની કિંમત સમીકરણ (11.2)માં મૂકતાં,
W = ma × \(\left(\frac{v^{2}-u^{2}}{2 a}\right)\)
∴ W = \(\frac{1}{2}\)m (v² – u²) ……… (11.4)

→ જો પદાર્થ સ્થાયી અવસ્થામાંથી પોતાની ગતિની શરૂઆત કરતો હું હોય, તો એટલે કે u = 0 હોય, તો
W = \(\frac{1}{2}\)mv² ………. (11.5)

→ આમ, સ્પષ્ટ છે કે m દળના પદાર્થને સ્થિર અવસ્થામાંથી વેગવાળી ગતિમાન અવસ્થામાં લાવવા માટે તેના પર \(\frac{1}{2}\)mv² જેટલું કાર્ય કરવું પડે છે, જે પદાર્થમાં ગતિ-ઊર્જા E_k સ્વરૂપે સંગ્રહ પામે છે.

→ તેથી m દળ તથા v જેટલા સમાન વેગથી ગતિ કરતા પદાર્થની ગતિ-ઊર્જાનું મૂલ્ય,
E_k = \(\frac{1}{2}\)mv² …………….. (11.6).

પ્રશ્ન 14.
ગતિ-ઊર્જાનાં ચાર ઉદાહરણો લખો.
ઉત્તરઃ
ગતિ-ઊર્જાનાં ઉદાહરણો

• રાઈફલમાંથી છોડેલી ગોળી ગતિ-ઊર્જા ધરાવે છે અને લક્ષ્યને વીંધે છે.
• પવનની ગતિ-ઊર્જાનો ઉપયોગ પવનચક્કી ચલાવવામાં થાય છે.
• વહેતા પાણીમાં સમાયેલી ગતિ-ઊર્જા વડે વિદ્યુત પેદા કરી શકાય છે.
• ઝાડ પરથી તૂટેલું નારિયેળ પૃથ્વી તરફ ગતિ કરે છે ત્યારે તે ગતિ-ઊર્જા ધરાવે છે.

પ્રશ્ન 15.
પદાર્થની ગતિ-ઊર્જા કઈ બાબતો પર આધાર રાખે છે? પદાર્થની ગતિ-ઊર્જા ક્યારેય ઋણ હોઈ શકે નહિ. શાથી?
ઉત્તરઃ
જો વેગ છે અચળ હોય, તો ગતિ-ઊર્જા E_K ∝ m. જ્યાં, m = દળ

• જો દળ m અચળ હોય, તો ગતિ-ઊર્જા E_K ∝ v².
  જ્યાં, D = વેગ
• જો પદાર્થનું દળ m અને તેનો વેગ v બંને બદલાતાં હોય, તો ગતિ-ઊર્જા E_k ∝ v²
• m દળના પદાર્થનો વેગ v હોય, તો તેની ગતિ-ઊર્જા E_k = \(\frac{1}{2}\)mv² હોય છે.
• હવે, પદાર્થનું દળ m હંમેશાં ધન હોય છે તથા વેગ ઈનો વર્ગ 2 ક્યારેય ઋણ હોઈ શકે નહિ. તેથી \(\frac{1}{2}\)mv²નું મૂલ્ય હંમેશાં ધન હોય છે, ત્રણ હોઈ શકે નહિ.

પ્રશ્ન 16.
નિયમિત વર્તુળમય ગતિ કરતા પદાર્થના કિસ્સામાં તેના પર લાગતા કેન્દ્રગામી બળ વડે થતું કાર્ય શૂન્ય હોય છે. સમજાવો.
ઉત્તરઃ
નિયમિત વર્તુળમય ગતિ કરતા પદાર્થની ઝડપ (વેગનું મૂલ્ય) હંમેશાં અચળ હોય છે, પણ તેના વેગની દિશા વર્તુળમાર્ગ પરના જે-તે બિંદુએ દોરેલા સ્પર્શકની દિશામાં હોય છે.

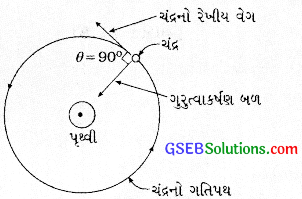
(આકૃતિ 11.7:ચંદ્રની પૃથ્વીની આસપાસની નિયમિત વર્તુળાકાર ગતિ)

આકતિ 11.7માં પૃથ્વીની આસપાસ વર્તુળમાર્ગે પરિક્રમણ કરતા ચંદ્રની ઝડપ સમગ્ર ગતિ દરમિયાન અચળ છે, એટલે કે u = v છે. તેથી W = \(\frac{1}{2}\)mv² – \(\frac{1}{2}\)mu² પરથી ચંદ્ર પર થતું કાર્ય w = 0 છે, એટલે કે ચંદ્રની ગતિ-ઊર્જામાં થતો ફેરફાર = 0 છે.

પ્રશ્ન 17.
સ્થિતિ-ઊર્જાની વ્યાખ્યા લખો અને તેનો SI એકમ જણાવો. સ્થિતિ-ઊર્જાનાં ચાર ઉદાહરણો આપો.
ઉત્તરઃ
પદાર્થની સંરચના અને / અથવા સ્થાનને કારણે, પદાર્થ કાર્ય કરવાની જે ક્ષમતા (ઊર્જા) ધરાવે છે, તેને પદાર્થની સ્થિતિ-ઊર્જા E_p કહે છે.
સ્થિતિ-ઊર્જા E_p નો SI એકમ જૂલ (J) છે.

સ્થિતિ-ઊર્જાનાં ઉદાહરણોઃ

• ઊંચાઈ પર બાંધેલા બંધમાં સંગ્રહાયેલું પાણી સ્થિતિ-ઊર્જા ધરાવે છે.
• દબાયેલી કે ખેંચાયેલી સ્પ્રિંગ સ્થિતિ-ઊર્જા ધરાવે છે.
• ધનુષ્ય પર ખેચેલું બાણ સ્થિતિઊર્જા ધરાવે છે.
• હાથ વડે ઊંચકેલો હથોડો સ્થિતિ-ઊર્જા ધરાવે છે.

પ્રશ્ન 18.
ગુરુત્વીય સ્થિતિ-ઊર્જાની વ્યાખ્યા લખો. m દળવાળા પદાર્થને સંદર્ભ સપાટી પરથી (જમીન પરથી) h ઊંચાઈએ લઈ જતા તેની ગુરુત્વીય સ્થિતિ-ઊર્જાનું સૂત્ર મેળવો.
ઉત્તર:
કોઈ પદાર્થને જમીન પરથી અમુક ઊંચાઈ પર લઈ જતાં તેની ઊર્જામાં વધારો થાય છે, કારણ કે પદાર્થને ઉપર લઈ જવા માટે ગુરુત્વાકર્ષણ બળની વિરુદ્ધમાં તેના પર કાર્ય કરવું પડે છે અને કરેલું આ કાર્ય તેમાં ઊર્જારૂપે સંગ્રહ પામે છે. તેને પદાર્થની ગુરુત્વીય સ્થિતિ-ઊર્જા કહે છે.

વ્યાખ્યા: જમીનથી ઉપર કોઈ બિંદુ પાસે પદાર્થને જમીન પરથી તે બિંદુ સુધી લઈ જવા માટે ગુરુત્વીય બળની વિરુદ્ધમાં તેના પર કરવા પડતા કાર્યને તે બિંદુ પાસે પદાર્થની ગુરુત્વીય સ્થિતિ-ઊર્જા કહે છે.

સૂત્રની તારવણી:

[ આકૃતિ 11.10]

આકૃતિ 11.10માં દર્શાવ્યા મુજબ m દળના પદાર્થને કે ઊંચાઈ સુધી લઈ જવામાં આવે છે. આ માટે બળની જરૂર પડશે.
→ પદાર્થને જમીનથી આપેલ ઊંચાઈ h સુધી લઈ જવા માટે જરૂરી લઘુતમ બળ (પદાર્થની અચળ વેગી ગતિ માટે) પદાર્થના વજન mg જેટલું છે.

→ હવે, પદાર્થમાં તેના પર કરેલા કાર્ય જેટલી ઊર્જા સંગ્રહ પામે છે.

→ ધારો કે, પદાર્થ પર ગુરુત્વીય બળની વિરુદ્ધમાં કરેલ કાર્ય જ છે. આમ, કરેલ કાર્ય W = બળ × સ્થાનાંતર
= mg × h
= mgh ………. (11.7)
પદાર્થ પર કરેલ કાર્ય mgh જેટલું છે. તેથી પદાર્થને mgh જેટલી ઊર્જા મળે છે, જે પદાર્થની ગુરુત્વીય સ્થિતિ-ઊર્જા E છે.
∴ Ep = mgh ………. (11.8)

નોંધઃ પૃથ્વીની સપાટી પર આવેલ કોઈ બિંદુ માટે h = 0 હોય છે. તેથી પૃથ્વીની સપાટી (જમીન) પર m દળના પદાર્થની ગુરુત્વીય સ્થિતિ-ઊર્જા શૂન્ય છે.
પણ પૃથ્વીની સપાટીથી (જમીનથી) કે જેટલી ઊંચાઈએ m દળના પદાર્થની ગુરુત્વીય સ્થિતિ-ઊર્જા mgh જેટલી હોય છે.

અગત્યની જાણકારી:
પદાર્થની કોઈ ઊંચાઈ પર સ્થિતિ-ઊર્જા જમીનની સપાટી પર કે પછી તમારા દ્વારા પસંદ કરવામાં આવેલ શૂન્યતલ પર આધાર રાખે છે. કોઈ પદાર્થની આપેલ સ્થિતિ માટે એક સમતલની સાપેક્ષમાં સ્થિતિ-ઊર્જાનું મૂલ્ય કંઈક હોઈ શકે, તો બીજા કોઈ સમતલની સાપેક્ષમાં સ્થિતિ-ઊર્જાનું મૂલ્ય કંઈક જુદું પણ હોઈ શકે છે.

પ્રશ્ન 19.
ગુરુત્વીય સ્થિતિ-ઊર્જાની અગત્યની ખાસિયત જણાવી, આકૃતિ દોરીને તેની સ્પષ્ટતા કરો. [2 ગુણ]
ઉત્તર:
m દળના પદાર્થને જમીનથી કે જેટલી ઊંચાઈએ અચળ વેગથી લઈ જવા માટે તેના પર લગાડવું પડતું લઘુતમ બળ તેના વજન mg જેટલું હોય છે. તેથી h ઊંચાઈએ પદાર્થની ગુરુત્વીય સ્થિતિ-ઊર્જા mgh જેટલી છે.

હવે, પદાર્થ પર mg વડે થયેલ એટલે કે ગુરુત્વીય બળ વડે થયેલ કાર્ય પદાર્થના પ્રારંભિક તથા અંતિમ સ્થાન પર આધાર રાખે છે. તેના ગતિપથ પર આધાર રાખતું નથી.

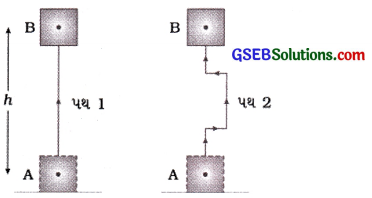
આકૃતિ 1.11માં આવી એક પરિસ્થિતિ દર્શાવેલ છે, જેમાં એક બ્લૉકને સ્થિતિનું સ્થાન A પરથી સ્થિતિ સ્થાન B સુધી બે જુદા જુદા પથ દ્વારા પહોંચાડાય છે. ધારો કે, AB = h. બંને સ્થિતિઓમાં પદાર્થ પર થયેલ કાર્ય mgh છે.

પ્રશ્ન 20.
ઊર્જા-સંરક્ષણનો નિયમ લખો અને તેની સ્પષ્ટતા કરો. [2 ગુણ)
ઉત્તર:
ઊર્જા સંરક્ષણનો નિયમઃ જ્યારે પણ ઊર્જાનું રૂપાંતરણ થાય છે ત્યારે તંત્રની કુલ ઊર્જા અચળ રહે છે.
આ નિયમ અનુસાર ઊર્જા ફક્ત એક સ્વરૂપમાંથી બીજા સ્વરૂપમાં રૂપાંતરિત થઈ શકે છે, પરંતુ તેની ઉત્પત્તિ કે વિનાશ થઈ શકતો નથી. રૂપાંતરણ પહેલાં અને રૂપાંતરણ બાદ કુલ ઊર્જા હંમેશાં અચળ રહે છે.
ઊર્જા સંરક્ષણનો નિયમ દરેક અવસ્થા તેમજ તેના દરેક રૂપાંતરણ માટે સાચો છે.

પ્રશ્ન 21.
પદાર્થની કુલ યાંત્રિક ઊર્જા એટલે શું? [1 ગુણ)
ઉત્તર:
પદાર્થની ગતિ-ઊર્જા E અને સ્થિતિ-ઊર્જા E ના સરવાળાને પદાર્થની કુલ યાંત્રિક ઊર્જા E કહે છે.

પ્રશ્ન 22.
સાબિત કરો કે મુક્ત પતન કરતા પદાર્થની કુલ યાંત્રિક ઊર્જા હંમેશાં અચળ જળવાઈ રહે છે.
ઉત્તર:
ધારો કે, પ્રારંભમાં m દળના એક પદાર્થને h ઊંચાઈએથી મુક્ત પતન કરાવવામાં આવે છે.

→ પ્રારંભમાં પદાર્થની સ્થિતિ-ઊર્જા mgh જેટલી છે અને ગતિ-ઊર્જા શૂન્ય છે, કારણ કે તેનો પ્રારંભિક વેગ (u) શૂન્ય છે.
પ્રારંભમાં પદાર્થની કુલ યાંત્રિક ઊર્જા = mgh + 0 = mgh છે.

→ જ્યારે પદાર્થ નીચે તરફ ગતિ કરે છે ત્યારે તેની સ્થિતિ-ઊર્જા ગતિ-ઊર્જામાં રૂપાંતરિત થાય છે.

→ જો કોઈ આપેલ ક્ષણે પદાર્થનો વેગ ઈ હોય, તો તેની ગતિ-ઊર્જા
\(\frac{1}{2}\)mv² થશે.

→ પદાર્થ જેમ જેમ નીચે આવતો જાય છે તેમ તેમ તેની સ્થિતિ-ઊર્જા જેટલા પ્રમાણમાં ઘટતી જાય છે તેટલા જ પ્રમાણમાં તેની ગતિઊર્જા વધતી જાય છે.

→ અંતિમ અવસ્થામાં જ્યારે પદાર્થ જમીન પર પહોંચે છે ત્યારે h = 0 થશે. તેથી તેની સ્થિતિ-ઊર્જા લઘુતમ (શૂન્ય) થશે અને પદાર્થનો અંતિમ વેગ મહત્તમ થશે. તેથી તેની ગતિ-ઊર્જા મહત્તમ થશે.
∴ અંતિમ સ્થિતિમાં પદાર્થની કુલ યાંત્રિક ઊર્જા = 0 + \(\frac{1}{2}\)mv²
= \(\frac{1}{2}\)mv² છે.

→ જોકે ગતિપથના દરેક બિંદુ પાસે પદાર્થની સ્થિતિ-ઊર્જા તથા ગતિઊર્જાનો સરવાળો અચળ રહે છે.

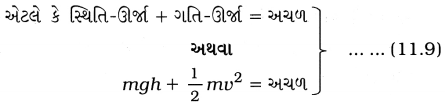
→ કોઈ પદાર્થની ગતિ-ઊર્જા E_k અને સ્થિતિ-ઊર્જા E_p ના સરવાળાને પદાર્થની કુલ યાંત્રિક ઊર્જા E કહે છે.
∴ સમીકરણ (11.9) પરથી સાબિત થાય છે કે, મુક્ત પતન કરતા પદાર્થની કુલ યાંત્રિક ઊર્જા હંમેશાં અચળ જળવાઈ રહે છે.
(અહીં પદાર્થની ગતિ પર હવાનો અવરોધ વગેરેને અવગણેલ છે.)

પ્રશ્ન 23.
ગુરુત્વાકર્ષણ બળની અસર હેઠળ મુક્ત પતન કરતા પદાર્થના કિસ્સામાં જરૂરી આકૃતિ તથા સૂત્ર મેળવીને દર્શાવો કે પદાર્થની યાંત્રિક ઊર્જા હંમેશાં અચળ જળવાઈ રહે છે.
ઉત્તર:

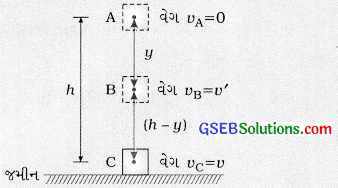
[આકૃતિ 1.12]

→ આકૃતિ 11.12માં દર્શાવ્યા મુજબ ધારો કે પ્રારંભમાં m દળનો પદાર્થ જમીનથી h ઊંચાઈએ સ્થિર છે. ત્યાંથી તેને મુક્ત કરવામાં આવે છે.

→ જેમ જેમ પદાર્થ નીચે આવે છે તેમ તેમ તેની સ્થિતિ-ઊર્જાના ભોગે ગતિ-ઊર્જા વધે છે.

બિંદુ A પાસે
પદાર્થ સ્થિર છે.
∴ પદાર્થની ગતિ-ઊર્જા (E_k)_A = 0 અને
પદાર્થની સ્થિતિ-ઊર્જા (E_p)_A = mgh (∵ જમીનથી પદાર્થની ઊંચાઈ h છે.)
∴ પદાર્થની કુલ યાંત્રિક ઊર્જા,
E = (E_k)_A + (E_p)_A = 0 + mgh = mgh …….. (11.10)

બિંદુ B પાસે
ધારો કે, પદાર્થ h ઊંચાઈએથી મુક્ત પતન કરી, y જેટલું અંતર અધોદિશામાં કાપે છે અને B બિંદુએ પહોંચે છે. જ્યાં તેનો વેગ v_B = v’ છે.
તો અચળ પ્રવેગી ગતિના સમીકરણ v² – u² = 2asનો ઉપયોગ કરતાં,
v_b² – 0² = 2gy
∴ v’² = 2gy (∵ v_B = v’)
∴ પદાર્થની ગતિ-ઊર્જા (E_k)_B = \(\frac{1}{2}\) mv_B²
= \(\frac{1}{2}\)mv’²
= mgy સેન
પદાર્થની સ્થિતિ-ઊર્જા (E_p)_B = mg (h – y) (∵ અત્રે જમીનથી પદાર્થની ઊંચાઈ = h – y)
∴ પદાર્થની કુલ યાંત્રિક ઊર્જા,
E = (E_k)_B + (E_p)_B
= mgy + mg (h – y)
= mgy + mgh – mgy
= mgh … … (11.11)

બિંદુ C પાસે
ધારો કે, અંતિમ અવસ્થામાં પદાર્થ જમીન પર v_c = v જેટલા વેગથી પહોંચે છે.
હવે, પ્રારંભિક બિંદુ Aથી અંતિમ બિંદુ C સુધીની પદાર્થની સમગ્ર ગતિ ધ્યાનમાં લેતાં …
v² – u² = 2as સૂત્ર પરથી,
v_C² – 0² = 2gh (∵ u = 0 અને a = g)
∴ v² = 2gh (∵ v_C = v)
∴ પદાર્થની ગતિ-ઊર્જા (E_k)_C = \(\frac{1}{2}\)mv_C²
= \(\frac{1}{2}\)mv²
= mgh અને
∴ પદાર્થની સ્થિતિ-ઊર્જા (E_p)_C = mg × 0 = 0 (∵ જમીનથી પદાર્થની ઊંચાઈ શૂન્ય છે.)
∴ પદાર્થની કુલ યાંત્રિક ઊર્જા,
E = (E_k)_C + (E_p)_C
= mgh + 0
= mgh …………… (11.12)
સમીકરણ (11.10), (11.11) અને (11.12) પરથી સ્પષ્ટ છે કે, જમીનથી જેટલી ઊંચાઈએથી મુક્ત પતન કરતા પદાર્થની યાંત્રિક ઊર્જા હંમેશાં અચળ (mgh જેટલી) રહે છે.

ઉપરની ચર્ચા પરથી એ પણ સ્પષ્ટ છે કે, જેમ જેમ પદાર્થ નીચે તરફ ગતિ કરે છે તેમ તેમ તેની ગુરુત્વીય સ્થિતિ-ઊર્જા E_p જેટલા પ્રમાણમાં ઘટતી જાય છે તેટલા જ પ્રમાણમાં તેની ગતિઊર્જા E_k વધતી જાય છે.

આકૃતિ 11.13માં ગતિ-ઊર્જા E , સ્થિતિ-ઊર્જા E, અને કુલ યાંત્રિક ઊર્જા E ઊંચાઈ સાથે કેવી રીતે બદલાય છે તે દર્શાવ્યું છે:

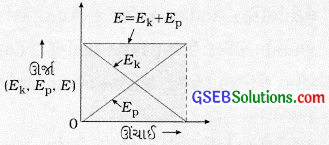
[આકૃતિ 11.13].

પ્રશ્ન 24.
ટૂંક નોંધ લખો: પાવર
ઉત્તર:
પાવર એ કરેલ કાર્યની ઝડપ માપે છે, એટલે કે કાર્ય કેટલું ઝડપથી કે ધીમેથી કરવામાં આવ્યું છે, તેનું માપન કરે છે.
→ કાર્ય કરવાના સમયદરને અથવા ઊર્જાના રૂપાંતરણના દરને પાવર હું કહે છે.

→ જો કોઈ પદાર્થ (એજન્ટ) t સમયમાં w જેટલું કાર્ય કરતો હોય, તો

→ પાવરનો SI એકમ છે. જેને વરાળયંત્રના શોધક જેમ્સ વૉટના માનમાં વૉટ (W) કહે છે.
∴ 1 W = 1 J s^-1

→ વૉટ (W): જો કોઈ પદાર્થ (એજન્ટ) 1 સેકન્ડમાં 1 જૂલ કાર્ય કરતો હોય, તો તેના ઊર્જા વપરાશનો દર 1 J s^-1 છે અથવા તેનો પાવર 1 W છે તેમ કહેવાય.

→ પાવરના મોટા એકમ kw (કિલોવૉટ) અને MW (મેગાવૉટ) છે.
જ્યાં, 1 kW = 10³w = 10³ J s^-1 અને
1 MW = 10⁶W = 10⁶ J s^-1

→ જો પદાર્થ(એજન્ટ)નો પાવર સમય સાથે બદલાતો હોય, તો એનો અર્થ એ થયો કે તે પદાર્થ (એજન્ટ) જુદા જુદા દરથી કાર્ય કરે છે.
તે વખતે સરેરાશ પાવરનો ખ્યાલ વધારે ઉપયોગી છે.

→

નોંધઃ બ્રિટિશ માપન-પદ્ધતિમાં પાવરનો એકમ હૉર્સપાવર (hp) વપરાય છે.
1 hp = 746 M છે.

પ્રશ્ન 25.
સરેરાશ પાવર વ્યાખ્યાયિત કરો.
ઉત્તર:
ઉપયોગમાં લીધેલ કુલ ઊર્જા અને તેના માટે લીધેલ કુલ સમયના ગુણોત્તરને સરેરાશ પાવર કહે છે.

પ્રશ્ન 26.
ઊર્જાનો | કાર્યનો મોટો વ્યાવસાયિક એકમ 1 kwh સમજાવો.
ઉત્તર:
પાવર = પરથી,
કાર્ય (અથવા ઊર્જા) = પાવર × સમય થાય.

→ આ હકીકત પરથી કાર્યનો (ઊર્જાનો) એકમ(પાવર × સમય)ના એકમના પદમાં લખી શકાય છે.
∴ કાર્યનો (ઊર્જાનો) મોટો એકમ = 1 kWh (1 કિલોવૉટ-અવર)
1 kWh: 1 kWh ઊર્જા (અથવા કાર્યો એટલે 1000 J s^-1ના
અચળ દરથી 1 કલાકમાં વપરાતી ઊર્જા (અથવા થતું કાય)
1 kWh = 1 kW × 1 h
= 1000 W × (60 × 60) s
= 1000 J S^-1 × 3600 s
= 36,00,000 J = 3.6 × 10⁶ J
આમ, 1 kWh = 3.6 × 10⁶ J

→ ઘરોમાં, ઉદ્યોગોમાં તથા વ્યાવસાયિક સંસ્થાઓમાં વપરાતી ઊર્જા
મોટા ભાગે કિલોવૉટ-અવર(1 kWh)માં દર્શાવાય છે.
1 kWh વિદ્યુત-ઊર્જા = 1 યુનિટ
1 યુનિટ = 3.6 × 10⁶ J વિદ્યુત-ઊર્જા

પ્રશ્ન 27.
નીચેના દાખલા ગણોઃ
પાઠ્યપુસ્તકનાં ઉદાહરણના દાખલા

1. કોઈ પદાર્થ પર 5N બળ લાગી રહ્યું છે. પદાર્થ બળની દિશામાં 2 m અંતર કાપે છે (આકૃતિ 11.14). જો બળ પદાર્થના સમગ્ર સ્થાનાંતર દરમિયાન લાગતું હોય, તો પદાર્થ પર થયેલું કાર્ય શોધો.

[આકૃતિ 11.14].
ઉકેલ:
પદાર્થ પર થયેલું કાર્ય W = Fs
= 5 N × 2 m
= 10 N m
= 10 J

2. એક કુલી 15 kg દ્રવ્યમાન જમીન પરથી ઉપાડીને જમીનથી 1.5m ઊંચાઈએ પોતાના માથા પર રાખે છે. તેના દ્વારા દ્રવ્યમાન ઉપર કરેલ કાર્યની ગણતરી કરો.
ઉકેલઃ
વજનનું દળ m = 15 kg તથા
સ્થાનાંતર = 1.5 m
કરેલ કાર્ય W = F × s = mg × s
= 15 kg × 10 m S^-2 × 1.5 m
= 225 kg m s^-2 m
= 225 Nm
= 225 J
કુલી દ્વારા 15 kg દળ ઉપર કરેલ કાર્ય 225 J છે.

3. 15 kg દળનો એક પદાર્થ 4m sીના સમાન વેગથી ગતિ કરે છે. પદાર્થની ગતિ-ઊર્જા કેટલી હશે?
ઉકેલઃ
પદાર્થનું દળ m = 15 kg
પદાર્થનો વેગ = 4 m s^-1
ગતિ-ઊર્જા E_k = \(\frac{1}{2}\) mઈ
= \(\frac{1}{2}\) × 15 kg × (4 m s^-1)² = 120 J
પદાર્થની ગતિ-ઊર્જા 120 J છે.

4. જો કોઈ કારનું દ્રવ્યમાન 1500 kg હોય, તો તેના વેગને 30 km h^-1થી વધારીને 60 km h^-1 કરવા માટે કેટલું કાર્ય કરવું પડશે?
ઉકેલ:
કારનું દળ m = 1500 kg
કારનો પ્રારંભિક વેગ u = 30 km h^-1
= \(\frac{30 \times 1000 \mathrm{~m}}{60 \times 60 \mathrm{~s}}\)
= 8.33 m s^-1
કારનો અંતિમ વેગ v = 60 km^-1
= \(\frac{60 \times 1000 \mathrm{~m}}{60 \times 60 \mathrm{~s}}\)
= 16.67 m s^-1
તેથી કારની પ્રારંભિક ગતિ-ઊર્જા.
E_ki = \(\frac{1}{2}\)mu²
= \(\frac{1}{2}\) × 1500 kg × (8.33m s^-1)²
= 52041.68 J
કારની અંતિમ ગતિ-ઊર્જા,
E_kf = \(\frac{1}{2}\) × 1500 kg × (16.67 m s^-1)²
= 208416.68 J
આમ, થયેલ કાર્ય = ગતિ-ઊર્જામાં ફેરફાર
= E_kf – E_ki
= 156375

5. 10 kg દળના એક પદાર્થને જમીનથી 6 મીટરની ઊંચાઈ સુધી લઈ જવામાં આવે છે. આ પદાર્થમાં સંગ્રહ પામતી ઊર્જાની ગણતરી કરો. (g = 9.8 m s^-2)
ઉકેલ:
પદાર્થનું દળ m = 10 kg
ઊંચાઈ h = 6 m
ગુરુવપ્રવેગ 9 = 9.8m s^-2
ગુરુત્વીય સ્થિતિ-ઊર્જા = mgh
= 10 kg × 9.8m s^-2 × 6 m
= 588 J.
પદાર્થમાં સંગ્રહ પામતી ઊર્જા 588 J છે.

6. 12 kg દળનો એક પદાર્થ જમીન પરથી અમુક ઊંચાઈ પર આવેલ છે. જો આ પદાર્થની સ્થિતિ-ઊર્જા 480 J હોય, તો પદાર્થની જમીનની સાપેક્ષ ઊંચાઈ શોધો. (g = 10 m s^-2 લો.)
ઉકેલ:
પદાર્થનું દળ m = 12 kg
સ્થિતિ-ઊર્જા E_p = 480 J
E_p = mgh
∴ 480 J = 12 kg × 10 m s^-2 × h
h = \(\frac{480 \mathrm{~J}}{120 \mathrm{~kg} \mathrm{~m} \mathrm{~s}^{-2}}\)= 4 m
પદાર્થ જમીનથી 4mની ઊંચાઈ પર આવેલ છે.

7. 400 N જેટલું સમાન વજન ધરાવતી બે છોકરીઓ એક 3 દોરડાની મદદથી 8m ઉપર ચડે છે. આપણે એક છોકરીનું નામ A અને બીજી છોકરીનું નામ B રાખીશું. આ કાર્ય પૂરું કરવા માટે છોકરી A 20 sનો સમય લે છે, જ્યારે છોકરી B 50 sનો સમય 3 લે છે. દરેક છોકરી દ્વારા વપરાયેલ પાવરની ગણતરી કરો.
ઉકેલ:
(i) છોકરી A દ્વારા વપરાયેલ પાવરઃ
છોકરી Aનું વજન mg = 400 N
છોકરી Aનું સ્થાનાંતર (ઊંચાઈ) h = 8 m
લીધેલ સમય t = 20 s

∴ P = \(\frac{m g h}{t}\)
= \(\frac{400 \mathrm{~N} \times 8 \mathrm{~m}}{20 \mathrm{~s}}\) = 160 W

(ii) છોકરી B દ્વારા વપરાયેલ પાવરઃ
છોકરી Bનું વજન mg = 400 N
છોકરી Bનું સ્થાનાંતર (ઊંચાઈ) h = 8m
લીધેલ સમય t = 50 s .
∴ પાવર P = \(\frac{m g h}{t}\)
= \(\frac{400 \mathrm{~N} \times 8 \mathrm{~m}}{50 \mathrm{~s}}\)
= 64 W
છોકરી A દ્વારા વપરાયેલ પાવર 160 % અને છોકરી B દ્વારા વપરાયેલ પાવર 64 W છે.

8. 50 kg દ્રવ્યમાન ધરાવતો એક છોકરો સીડીનાં 45 પગથિયાં દોડીને ૭ માં ચઢી જાય છે. જો દરેક પગથિયાની ઊંચાઈ 15 cm હોય, તો તેનો પાવર શોધો. (gનું મૂલ્ય 10 m s^-2 લો.)
ઉકેલ:
છોકરાનું વજન mg = 50 kg × 10 m s^-2 = 500 N
બધાં પગથિયાંની ઊંચાઈ h = 45 × \(\frac{15}{100}\) m = 6.75 m
ચઢવા માટે લીધેલ સમય t = 9 s

= \(\frac{m g h}{t}\)
∴ P = \(\frac{500 \mathrm{~N} \times 6.75 \mathrm{~m}}{9 \mathrm{~s}}\) = 375 W
આમ, છોકરાનો પાવર 375 W છે.

9. 60 W નો એક વિદ્યુત બલ્બ દરરોજ 6 કલાક વપરાય છે. બલ્બ દ્વારા એક દિવસમાં ખર્ચાતી ઊર્જાના યુનિટોની ગણતરી કરો.
ઉકેલઃ
વિદ્યુત બલ્બનો પાવર = 60 w
= 0.06 kw
સમય t = 6 h
ઊર્જા = પાવર × લીધેલ સમય
= 0.06 kW × 6 h
= 0.36 kWh = 0.36 યુનિટો
બલ્બ દ્વારા એક દિવસમાં 0.36 યુનિટો વપરાશે.

હેતુલક્ષી પ્રશ્નોત્તર
નીચેના પ્રશ્નોના એક શબ્દ કે એક વાક્યમાં ? (1થી 10 શબ્દોની મર્યાદામાં) ઉત્તર લખો:

પ્રશ્ન 1.
કાર્ય એ શાનું ગુણનફળ છે?
ઉત્તરઃ
બળ અને બળની દિશામાં સ્થાનાંતરનું

પ્રશ્ન 2.
SI પદ્ધતિમાં કાર્યનો એકમ શું છે?
ઉત્તરઃ
જૂલ

પ્રશ્ન 3.
વૉટ શાનો એકમ છે?
ઉત્તરઃ
પાવર

પ્રશ્ન 4.
વીજળીના વપરાશના માપન માટે વપરાતો વ્યવહારુ એકમ કયો છે?
ઉત્તરઃ
યુનિટ કે કિલોવૉટ-અવર

પ્રશ્ન 5.
1 હોર્સ પાવર (Horsepower) બરાબર કેટલા વૉટ?
ઉત્તરઃ
746 વૉટ

પ્રશ્ન 6.
પદાર્થની ગતિ-ઊર્જા શોધવાનું સૂત્ર જણાવો.
ઉત્તરઃ
E = \(\frac{1}{2}\)mv²

પ્રશ્ન 7.
પદાર્થ પર બાહ્યબળ લાગે છે. પરિણામે તે પ્રવેગી ગતિ કરે છે, તો શું એ શક્ય છે કે તે બળ વડે થતું કાર્ય શૂન્ય હોય? શક્ય હોય તો તેનું એક ઉદાહરણ આપો.
ઉત્તરઃ
હા, શક્ય છે.
ઉદાહરણઃ નિયમિત વર્તુળાકાર ગતિ (અહીં પદાર્થ પર લાગતું બળ હંમેશાં તેના સ્થાનાંતરને લંબરૂપે હોય છે.)

પ્રશ્ન 8.
પદાર્થ પર કાર્ય થવા માટે શું જરૂરી છે?
ઉત્તરઃ
પદાર્થ પર કાર્ય થવા માટે પદાર્થ પર બળ લાગવું જરૂરી છે અને તેનું સ્થાનાંતર થવું જરૂરી છે. તદઉપરાંત, બળ અને સ્થાનાંતર વચ્ચેનો ખૂણો θ ≥ 90° હોવો જોઈએ નહીં.

પ્રશ્ન 9.
કાર્ય કેવી ભૌતિક રાશિ છે? સદિશ કે અદિશ?
ઉત્તરઃ
કાર્ય અદિશ ભૌતિક રાશિ છે.

પ્રશ્ન 10.
કાર્યની વ્યાખ્યા આપો.
ઉત્તરઃ
પદાર્થ પર બળ લાગતું હોય તે સમયગાળા દરમિયાન પદાર્થનું સ્થાનાંતર બળની દિશામાં થતું હોય, તો બળ અને સ્થાનાંતરના ગુણાકારને કાર્ય કહે છે.

પ્રશ્ન 11.
1 kWh ની વ્યાખ્યા આપો.
ઉત્તરઃ
1 k% જેટલા અચળ દરે 1 કલાકમાં થતા કાર્યને 1 કિલોવૉટ અવર (kWh) કહે છે.

પ્રશ્ન 12.
ઊર્જા-સંરક્ષણનો નિયમ લખો.
ઉત્તરઃ
“જ્યારે પણ ઊર્જાનું રૂપાંતરણ થાય છે ત્યારે તંત્રની કુલ ઊર્જા અચળ રહે છે.” અથવા “સમગ્ર બ્રહ્માંડની કુલ ઊર્જા અચળ રહે છે.”

પ્રશ્ન 13.
જો પદાર્થ પર લાગતું સમગ્ર બળ કાર્ય માટે જવાબદાર હોય, તો બળ અને સ્થાનાંતર વચ્ચેનો ખૂણો કેટલો હશે?
ઉત્તરઃ
શૂન્ય

પ્રશ્ન 14.
યાંત્રિક ઊર્જા શું છે?
ઉત્તરઃ
પદાર્થની ગતિ-ઊર્જા E_k અને સ્થિતિ-ઊર્જા E_pના સરવાળાને પદાર્થની યાંત્રિક ઊર્જા E કહે છે. (E = E_k + E_p)

પ્રશ્ન 15.
પદાર્થ પર બળ લાગવા છતાં કાર્ય શૂન્ય થતું હોય તેવું એકઉદાહરણ આપો.
ઉત્તરઃ
દીવાલને બાહ્યબળ લગાડવા છતાં તે સ્થાનાંતરિત થતી નથી.
તેથી અહીં બાહ્યબળ વડે થતું કાર્ય શૂન્ય છે.

પ્રશ્ન 16.
ચાવીવાળી ઘડિયાળ અથવા ચાવીવાળા રમકડામાં ઊર્જા ક્યા? સ્વરૂપે સંગૃહીત થયેલી હોય છે?
ઉત્તરઃ
સ્થિતિસ્થાપકીય સ્થિતિ-ઊર્જા

પ્રશ્ન 17.
યંત્રશાસ્ત્રમાં ઊર્જાનાં બે મુખ્ય સ્વરૂપો ક્યાં છે?
ઉત્તરઃ

• સ્થિતિ-ઊર્જા અને
• ગતિ-ઊર્જા

પ્રશ્ન 18.
પદાર્થની ગતિ-ઊર્જા એટલે શું?
ઉત્તરઃ
પદાર્થ પોતાની ગતિને કારણે કાર્ય કરવાની જે ક્ષમતા ધરાવે છે એટલે કે ઊર્જા ધરાવે છે, તેને પદાર્થની ગતિ-ઊર્જા કહે છે.

પ્રશ્ન 19.
પદાર્થની સ્થિતિ-ઊર્જા એટલે શું?
ઉત્તરઃ
પદાર્થની સંરચના અને / અથવા સ્થાનને કારણે, પદાર્થ કાર્ય કરવાની જે ક્ષમતા (ઊર્જા) ધરાવે છે, તેને પદાર્થની સ્થિતિ-ઊર્જા કહે છે.

પ્રશ્ન 20.
મુક્ત પતન કરતા પદાર્થના કિસ્સામાં યાંત્રિક ઊર્જા સંરક્ષણનોનિયમ જણાવો.
ઉત્તરઃ
પદાર્થના મુક્ત પતન દરમિયાન તેના ગતિપથના કોઈ બિંદુ પાસે સ્થિતિ-ઊર્જામાં જેટલો ઘટાડો થાય છે તેટલો જ તેની ગતિ-ઊર્જામાં વધારો થાય છે, અર્થાત્ સ્થિતિ-ઊર્જા + ગતિ-ઊર્જા = અચળ.

પ્રશ્ન 21.
સરેરાશ પાવરનું મૂલ્ય શોધવાનું સૂત્ર લખો.
ઉત્તરઃ

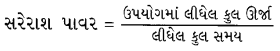
ખાલી જગ્યા પૂરો

પ્રશ્ન 1.
1 વૉટ-સેકન્ડ = ………………….. જૂલ
ઉત્તરઃ
1

પ્રશ્ન 2.
એક બાળક મજબૂત પાતળી દોરીના છેડે 20 g દળના પથ્થરને બાંધી તેને વર્તુળાકાર માર્ગ પર ગતિ કરાવે છે, તો તેના વડે થયેલ કાર્ય ………………….. જૂલ છે.
ઉત્તરઃ
શૂન્ય

પ્રશ્ન 3.
120 g દળવાળા એક પદાર્થને ઊર્ધ્વદિશામાં 5mની ઊંચાઈ સુધી લઈ જવામાં આવે છે, તો થયેલ કાર્ય ………………….. જૂલ છે. (g = 10 m s^-2 લો.)
ઉત્તરઃ
6

પ્રશ્ન 4.
50 kg દળવાળી હેતલ 30 kg દળના પદાર્થને લઈને ? 20 m ઊંચાઈ સુધી 40 sમાં ચડે છે, તો તેનો પાવર ………………….. છે. (g = 10 m s^-2 લો.)
ઉત્તરઃ
400

પ્રશ્ન 5.
ચંદ્ર પરનો ગુરુત્વપ્રવેગ એ પૃથ્વી પરના ગુરુતપ્રવેગ કરતાં છઠ્ઠા ‘ભાગનો છે. એક વ્યક્તિ પૃથ્વીની સપાટી પર 2 m ઊંચો કૂદકો લગાવી શકે છે. તે ચંદ્રની સપાટી પર ………………….. m ઊંચોકૂદકો લગાવી શકે.
ઉત્તરઃ
12

પ્રશ્ન 6.
60 wનો એક ઇલેક્ટ્રિક બલ્બ દરરોજ 10 કલાક ચાલુ રહે છે. આ બલ્બ વડે જૂન માસમાં ………………….. યુનિટ વિદ્યુત-ઊર્જા વપરાય.
ઉત્તરઃ
18

પ્રશ્ન 7.
40 N વજન ધરાવતા પદાર્થને 10 m જેટલી ઊંચાઈએથી મુક્ત પતન કરાવવામાં આવે છે. જ્યારે તે જમીનને અડકવાની તૈયારીમાં હોય ત્યારે તેની ગતિ-ઊર્જા …………………… J હશે.
ઉત્તરઃ
400

પ્રશ્ન 8.
3730 watt = ………………….. hp
ઉત્તરઃ
5

પ્રશ્ન 9.
એક પદાર્થ પર અચળ બળ 1 N લાગવાને કારણે તેનું સ્થાનાંતર બળની દિશામાં 1 m જેટલું થાય છે, તો થતું કાર્ય ………………….. J છે.
ઉત્તરઃ
1

નીચેના વિધાનો ખરાં છે કે ખોટાં તે જણાવો?

પ્રશ્ન 1.
પદાર્થમાં રહેલી કાર્ય કરવાની ક્ષમતાને ઊર્જા કહે છે.
ઉત્તરઃ
ખરું

પ્રશ્ન 2.
કાર્ય અને ઊર્જાના એકમ સમાન છે.
ઉત્તરઃ
ખરું

પ્રશ્ન 3.
પદાર્થની સ્થિતિ-ઊર્જા એ સાપેક્ષ છે.
ઉત્તરઃ
ખરું

પ્રશ્ન 4.
પાવર = કાર્ય × કાર્ય કરવા લીધેલો સમય
ઉત્તરઃ
ખોટું

પ્રશ્ન 5.
કોઈ પદાર્થને 10 N જેટલા બળથી ઊર્ધ્વદિશામાં ફેંકતા તે જ્યારે મહત્તમ ઊંચાઈએ પહોંચે ત્યારે તેની ગતિ-ઊર્જા શૂન્ય હોય છે.
ઉત્તરઃ
ખરું

પ્રશ્ન 6.
1 યુનિટ વિદ્યુત-ઊર્જા એટલે 1000 જૂલ વિદ્યુત-ઊર્જા.
ઉત્તરઃ
ખોટું

પ્રશ્ન 7.
કાર્ય કરવાના સમયદરને પાવર કહે છે.
ઉત્તરઃ
ખરું

પ્રશ્ન 8.
1 મેગાવૉટ (MW) પાવર એટલે 10⁶ વૉટ (W) પાવર.
ઉત્તરઃ
ખરું

પ્રશ્ન 9.
પાવર અને ઊર્જા બને અદિશ રાશિઓ છે.
ઉત્તરઃ
ખરું

પ્રશ્ન 10.
પદાર્થ દ્વારા કાર્ય કરવામાં આવે, તો તેની ઊર્જામાં ઘટાડો થાય છે.
ઉત્તરઃ
ખરું

પ્રશ્ન 11.
સ્થિતિ-ઊર્જા અને ગતિ-ઊર્જાના તફાવતને યાંત્રિક ઊર્જા કહે છે.
ઉત્તરઃ
ખોટું

પ્રશ્ન 12.
કાર્ય એ પાવર અને સમયનું ગુણનફળ છે.
ઉત્તરઃ
ખરું

નીચેના પ્રશ્નોના માગ્યા પ્રમાણે ટૂંકમાં ઉત્તર લખો:

પ્રશ્ન 1.
બળ અને સ્થાનાંતર વચ્ચેનો ખૂણો વધતા કાર્યનું મૂલ્ય ? ઘટે છે. સહમત કે અસહમત?
ઉત્તર:
સહમત

પ્રશ્ન 2.
સ્પ્રિંગની સ્થિતિ-ઊર્જા વિશે નીચેનામાંથી સાચું પસંદ કરો:
(i) તેને દબાવતા વધે છે.
(ii) તેને દબાવતા ઘટે છે.
ઉત્તરઃ
(i) તેને દબાવતા વધે છે.

પ્રશ્ન 3.
યથાર્થ જોડકાં જોડો.

A	B
1. કાર્ય	P. N
2. પાવર	q. Nm
	r. N m s
	s. N m s-1

ઉત્તરઃ

A	B
1. કાર્ય	q. Nm
2. પાવર	s. N m s-1

પ્રશ્ન 4.
10 kg દળ ધરાવતો પદાર્થ પૃથ્વીની સપાટીથી કેટલી ઊંચાઈએ હોય ત્યારે તેની સ્થિતિ-ઊર્જા 200 J હોય? (g = 10 ms^-2 લો.)
ઉત્તરઃ
સ્થિતિ-ઊર્જા E_p = mgh
∴ h = \(\frac{E_{\mathrm{p}}}{\mathrm{mh}}\)
= \(\frac{200}{10 \times 10}\)
= 2 m

પ્રશ્ન 5.
યથાર્થ જોડકાં જોડો :

A	B
1. 1 kW	a. 10-3 J s-1
2. 1 kWh	b. 103 J s-1
	c. 106 J s-1
	d. 1 યુનિટ

ઉત્તર:

A	B
1. 1 kW	b. 103 J s-1
2. 1 kWh	d. 1 યુનિટ

પ્રશ્ન 6.
20 યુનિટ વિદ્યુત-ઊર્જાને Ws એકમમાં રજૂ કરો.
ઉત્તર:
20 યુનિટ = 20 × 3.6 × 105
= 7.2 × 10⁷ Ws (∵ J = Rs છે.)

પ્રશ્ન 7.
પૃથ્વી તરફ મુક્ત પતન કરતા પદાર્થની કુલ ઊર્જા વધતી જાય છે. સહમત કે અસહમત?
ઉત્તર:
અસહમત

પ્રશ્ન 8.
100 wના 5 વિદ્યુત બલ્બ 8 કલાક ચાલુ રહે, 3 તો 1 દિવસમાં કેટલા યુનિટ વિદ્યુત-ઊર્જા વપરાય?
ઉત્તર:
1 દિવસમાં વપરાતી વિદ્યુત-ઊર્જા = 5 × 100 W × 8h
= 4000 Wh
= 4 kWh
= 4 યુનિટ

પ્રશ્ન 9.
એક પાણીના પંપનો પાવર 2 kW છે. આ પંપ વડે 10 m જેટલી ઊંચાઈએ 1 મિનિટમાં કેટલા લિટર પાણી ચઢાવી શકાય? (g = 10 m s^-2 લો.)
ઉત્તર:
પાવર P = \(\frac{W}{t}\) = \(\frac{mgh}{t}\)
∴ પાણીનું દળ m = \(
= [latex]\frac{\left(2 \times 10^{3}\right) \times 60}{10 \times 10}\)
= 1200 kg
= 1200 × 10³ g
પણ CGS એકમ પદ્ધતિમાં પાણીની ઘનતા = 1 g cm^-3 છે.
∴ પાણીનું કદ = 1200 × 10³ cm³
= 1200 લિટર (∵ 1 લિટર = 10³ cm³ છે.)

પ્રશ્ન 10.
એક પદાર્થને પૃથ્વીની સપાટીથી ૧ જેટલી ઊંચાઈએ આવેલા સ્થાન આગળ સીધા માર્ગે ગતિ કરાવીને લઈ જતાં લઘુતમ (બાહ્ય)બળ દ્વારા થતું કાર્ય W₁ છે અને વાંકાચૂકા માર્ગે લઈ જતાં થતું કાર્ય W₂ છે, તો W₁ અને W₂ ની સરખામણી કરો.
ઉત્તર:
લઘુતમ (બાહ્ય)બળ એટલે કે પદાર્થના વજન mg જેટલું બાહ્યબળ.

હવે, લઘુતમ (બાહ્ય)બળ દ્વારા થતું કાર્ય, પદાર્થના ગતિમાર્ગના માત્ર પ્રારંભિક અને અંતિમ સ્થાન પર આધાર રાખે છે. તેથી અહીં W₁ = W₂ અથવા \(\frac{W_{1}}{W_{2}}\) = 1.

નીચેના દરેક પ્રશ્ન માટે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરી ઉત્તર લખો

પ્રશ્ન 1.
કાર્ય થવા માટે શું જરૂરી છે? (સાચું વિધાન પસંદ કરો.)
(1) બળ લાગવું જરૂરી છે.
(2) સ્થાનાંતર થવું જરૂરી છે.
(3) બળની દિશામાં સ્થાનાંતર થવું જરૂરી છે.

A. વિધાન 1
B વિધાન 2.
C. વિધાન 3
D. વિધાન 1 અને 3
ઉત્તરઃ
D. વિધાન 1 અને 3

પ્રશ્ન 2.
10 kg દળનો એક પદાર્થ 5 m ત્રિજ્યાવાળા વર્તુળાકાર માર્ગ પર 10 m s^-1 ની ઝડપથી ગતિ કરે છે, તો એક પરિક્રમણમાં થતું કાર્ય …………. J થાય.
A. 2000 π
B. 1000 π
C. 500 π
D. શૂન્ય

Hint: અહીં પદાર્થ નિયમિત વર્તુળાકાર ગતિ કરે છે. તેના પર લાગતા કેન્દ્રગામી બળ અને વર્તુળમાર્ગ પરના જે-તે બિંદુએ તેના સ્થાનાંતરની દિશા વચ્ચેનો ખૂણો 90° છે.
તેથી W = F × s = 0 × s = 0.
ઉત્તરઃ
D. શૂન્ય

પ્રશ્ન 3.
ગતિ-ઊર્જા, સ્થિતિ-ઊર્જા અને યાંત્રિક ઊર્જા પૈકી કઈ ઊર્જા ઋણ ન હોઈ શકે?
A. ગતિ-ઊર્જા
B. સ્થિતિ-ઊર્જા
C. યાંત્રિક ઊર્જા
D. સ્થિતિ-ઊર્જા અને યાંત્રિક ઊર્જા
ઉત્તરઃ
A. ગતિ-ઊર્જા

પ્રશ્ન 4.
પદાર્થ પર કરેલું કાર્ય …………………. માં થતા ફેરફાર જેટલું હોય છે.
A. માત્ર ગતિ-ઊર્જા
B. માત્ર સ્થિતિ-ઊર્જા
C. માત્ર યાંત્રિક ઊર્જા
D. ઊર્જા
ઉત્તરઃ
D. ઊર્જા

પ્રશ્ન 5.
60 kg દળવાળો એક માણસ 15 kg દળવાળી પાણીની ડોલ લઈને 20 m ઊંચાઈએ ચઢે છે, તો થતું કાર્ય …………… kJ થાય. (g = 9.8 m s^-2)
A. 15
B. 20
C. 150
D. 1.5

Hint: કુલ દળ m = માણસનું દળ + ડોલનું દળ
= 60 kg + 15 kg
= 75 kg
કાર્ય = mgh
= (75) (9.8) (20)
= 14,700 J.
≈ 15,000 J = 15 × 10³ J = 15 kJ
[નોંધઃ જો g = 10 msી લેવામાં આવે, તો જવાબ exact (યથાર્થ) 15,000 J = 15 kઈ આવશે.]
ઉત્તરઃ
A. 15

પ્રશ્ન 6.
20 kg દળવાળા એક બૉક્સને સમક્ષિતિજ સપાટી પર બળ F લગાવીને અચળ વેગથી ખેંચવામાં આવે છે. જો ઘર્ષણબળ 49 N હોય, તો 10 m સ્થાનાંતર દરમિયાન થતું કાર્ય …………. J થાય.
A. 490
B. 245
C. 980
D. શૂન્ય

Hint: બૉક્સ અચળ વેગથી ગતિ કરે છે. એટલે કે તેના પર સંતુલિત બળો લાગે છે. સંતુલિત બળોનું પરિણામી બળ શૂન્ય હોય છે. આથી બૉક્સના સ્થાનાંતર દરમિયાન થતું કાર્ય શૂન્ય થશે.
ઉત્તરઃ
D. શૂન્ય

પ્રશ્ન 7.
બે પદાર્થનાં દળ અનુક્રમે 1 kg અને 4 kg છે. જો તેમની ગતિ-ઊર્જા 2 : 1 પ્રમાણમાં હોય, તો તેમની ઝડપનો ગુણોત્તર ……… છે.
A. 2√2 : 1
B. 1 : √2
C. 1 : 2
D. 2: 1

Hint:

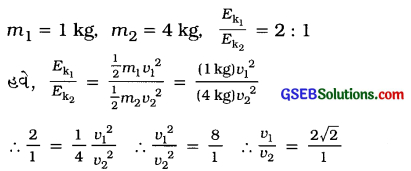
ઉત્તરઃ
A. 2√2 : 1

પ્રશ્ન 8.
એક કારનું એન્જિન 1500 kg દળવાળી કારને સમતલ રસ્તા પર 5 m s^-1ના અચળ વેગથી ગતિમાં રાખે છે. જો ઘર્ષણબળ 1000 N હોય, તો એન્જિનનો પાવર …….. છે.
A. 5 kW
B. 7.5 kW
C. 15 kW
D. 75 kW

Hint: v = 5 m s^-1, m = 1500 kg, F = 1000 N
W = F × s
∴ P = \(\frac{W}{t}\) = \(\frac{F \times s}{t}\) = F × v (∵ \(\) = v છે.)
∴ P = (1000 N) × (5 m s^-1) = 5000 w
P = 5 kW
ઉત્તરઃ
A. 5 kW

પ્રશ્ન 9.
એક જળવિદ્યુત-મથકમાં બંધની ઊંચાઈ 20 m છે. બંધ પરથી 1 sમાં કેટલા કિગ્રા પાણી ટર્બાઇન પર પડે, તો 1 MW પાવર ઉત્પન્ન થઈ શકે? (g = 10 m s^-2)
A. 5000 kg
B. 10,000 kg
C. 500 kg
D. 7500 kg

Hint: h = 20 m, P = 1 MW = 10⁶ w, t = 1s,
g = 10 m s^-2
∴ P = \(\frac{W}{t}\) = \(\frac{mgh}{t}\)
∴ m = \(\frac{P \times t}{g \times h}\) = \(\frac{10^{6} \times 1}{10 \times 20}\) = 5000 kg
ઉત્તરઃ
A. 5000 kg

પ્રશ્ન 10.
એક ગતિમાન પદાર્થની ઝડપ બમણી થતાં તેની ગતિ-ઊર્જા ……………………. થાય.
A. બમણી
B. ત્રણ ગણી
C. ચાર ગણી
D. અડધી

Hint: ગતિ-ઊર્જા E_k = \(\frac{1}{2}\) mv²
હવે, તેની ઝડપ બમણી કરતાં,
E_kk = \(\frac{1}{2}\)m (2v)²
= \(\frac{1}{2}\)mv² × 4 = 4 E_k
આમ, પદાર્થની ગતિ-ઊર્જા ચાર ગણી થાય.
ઉત્તરઃ
C. ચાર ગણી

પ્રશ્ન 11.
એક પદાર્થને 20 m sની ઝડપથી શિરોલંબ દિશામાં ફેંકવામાં આવે છે, તો કેટલી ઊંચાઈ પર તેની ગતિ-ઊર્જા અને સ્થિતિ-ઊર્જા સમાન થશે? (g = 10 m s^-2)
A. 10 m
B. 20 m
C. 15 m
D. 5 m

Hint: u = 20 m s^-1
યાંત્રિક ઊર્જા-સંરક્ષણના નિયમ પરથી,

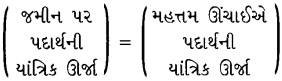
∴ E_k1 + E_p1 = E_k2 + E_p2
∴ \(\frac{1}{2}\)mu² + 0 = 0 + mgh
(∵ જમીન પર પદાર્થની સ્થિતિ-ઊર્જા U₁ = 0 અને મહત્તમ ઊંચાઈએ પદાર્થની ગતિ-ઊર્જા E_k2 = 0 હોય છે.)
∴ h = \(\frac{u^{2}}{2 g}\) = \(\frac{(20)^{2}}{2 \times 10}\) = 20 m
ઉત્તરઃ
B. 20 m

પ્રશ્ન 12.
1 kWh = ………. J
A. 36 × 10⁶
B. 3.6 × 10⁶
C. 3.6 × 10⁷
D. 3.6 × 10⁵

Hint: 1 kWh = (1 kW) (hour)
= (1000 J s^-1) (3600 s)
= 36 × 10⁵ J = 3.6 × 10⁶ J
ઉત્તરઃ
B. 3.6 × 10⁶

પ્રશ્ન 13.
સ્પ્રિંગને દબાવતાં તેની સ્થિતિ-ઊર્જા ….
A. અચળ રહે
B. ઘટે
C. વધે
D. વિશે કાંઈ ન કહી શકાય
ઉત્તરઃ
C. વધે

પ્રશ્ન 14.
કાર્યનો એકમ કયો છે?
A. ન્યૂટન / મીટર
B જૂલ / સેકન્ડ
C. ન્યૂટન-મીટર
D. વૉટ
ઉત્તરઃ
C. ન્યૂટન-મીટર

પ્રશ્ન 15.
પાવર એ શું છે?
A. વેગમાનના ફેરફારનો દર
B. ઊર્જાના ફેરફારનો દર
C. વેગના ફેરફારનો દર
D. બળના ફેરફારનો દર
ઉત્તરઃ
B. ઊર્જાના ફેરફારનો દર

પ્રશ્ન 16.
55 kg દળ ધરાવતી વ્યક્તિ દીવાલને ધક્કો મારે છે. આ વ્યક્તિ
દ્વારા થયેલ કાર્ય કેટલા જૂલ છે?
A. 55 J
B. 550 J
C. 5.5 J
D. શૂન્ય

Hint: દીવાલને ધક્કો મારતાં તેનું સ્થાનાંતર થતું નથી. આથી વ્યક્તિ દ્વારા થયેલ કાર્ય શૂન્ય થશે.
ઉત્તરઃ
D. શૂન્ય

પ્રશ્ન 17.
4 kg દળ ધરાવતા પદાર્થનું વેગમાન 20 kg m sી હોય, તો તેની ગતિ-ઊર્જા કેટલી હશે?
A. 25 J
B. 50 J
C. 75 J
D. 100 J

Hint: E_k = \(\frac{p^{2}}{2 m}\) = \(\frac{(20)^{2}}{2(4)}\) = \(\frac{400}{8}\) = 50 J
ઉત્તરઃ
B. 50 J

પ્રશ્ન 18.
એક 2 kg દળના પદાર્થને 3 m s^-1ના વેગથી ઊર્ધ્વદિશામાં ફેંકવામાં આવે છે. આ પદાર્થની મહત્તમ સ્થિતિ-ઊર્જા કેટલી હશે?
A. 18 J
B. 4.5 J
C. 9 J
D. 2.25 J

Hint: મહત્તમ ઊંચાઈએ પદાર્થની સ્થિતિ-ઊર્જા મહત્તમ હશે. આ સ્થિતિ-ઊર્જા એ પ્રારંભિક ગતિ-ઊર્જા જેટલી હશે.
E_k = \(\frac{1}{2}\)mv² = \(\frac{1}{2}\) × (2 kg) × (૩m/s)² = 9J
ઉત્તરઃ
C. 9 J

પ્રશ્ન 19.
પદાર્થની ગતિ-ઊર્જા …
A. માત્ર તેના દળ પર આધાર રાખે છે.
B. માત્ર તેની ઝડપ પર આધાર રાખે છે.
C. તેના દળ તેમજ તેની ઝડપ બંને પર આધાર રાખે છે.
D. તેના દળ કે ઝડપ પર આધારિત નથી.
ઉત્તરઃ
C. તેના દળ તેમજ તેની ઝડપ બંને પર આધાર રાખે છે.

પ્રશ્ન 20.
100 g દળવાળો પદાર્થ 1 m s^-1 જેટલી ઝડપે ગતિ કરે છે. તેની ગતિ-ઊર્જા કેટલા ફૂલ હશે?
A. 50 J
B. 5 J
C. 0.5 J
D. 0.05 J

Hint: E_k = \(\frac{1}{2}\)mv²
= \(\frac{1}{2}\) (100 × 10^-3) (1)²
= 50 × 10^-3
= 0.05 J
ઉત્તરઃ
D. 0.05 J

પ્રશ્ન 21.
સમતલ સપાટી પર પ્રવેગી ગતિ કરતી કારની ઝડપ પ્રારંભ કરતાં ચાર ગણી થાય ત્યારે તેની સ્થિતિ-ઊર્જામાં શો ફેરફાર થાય?
A. કોઈ ફેરફાર થશે નહિ.
B. બે ગણી થશે.
C. ચાર ગણી થશે.
D. સોળ ગણી થશે.
ઉત્તરઃ
A. કોઈ ફેરફાર થશે નહિ.

પ્રશ્ન 22.
રાઈફલમાંથી 20 g દળની ગોળી છૂટ્યા બાદ 4 sમાં 30 m જેટલું અંતર કાપે છે. ગોળીની ઝડપ અચળ ધારો અને તેની ગતિ-ઊર્જા શોધો.
A. 0.5625 J
B. 56.25 J
C. 30.08 J
D. 1.125 J

Hint: ગોળીની અસળ ઝડે૫ v = \(\) = 7.5 m s^-1
ગતિ-ઊર્જા E_k = \(\frac{1}{2}\)mv²
= \(\frac{1}{2}\) × (0.02 kg) 7.5 ms^-1)²
= 0.5625 J
ઉત્તરઃ
A. 0.5625 J

પ્રશ્ન 23.
જમીન પરથી એક પદાર્થને 10 J જેટલી ગતિ-ઊર્જા સાથે ઊર્ધ્વદિશામાં ફેંકવામાં આવે છે. તે 5m જેટલી મહત્તમ ઊંચાઈ પ્રાપ્ત કરતો હોય, તો તેનું દળ શોધો. (g = 10 m s^-2)
A. 2 kg
B. 20 kg
C. 0.02 kg
D. 0.2 kg

Hint: પદાર્થ જ્યારે મહત્તમ ઊંચાઈ પ્રાપ્ત કરે છે ત્યારે તેની સમગ્ર ગતિ-ઊર્જા તેની ગુરુત્વીય સ્થિતિ-ઊર્જામાં રૂપાંતરિત થાય છે. તેથી E_k = E_p
∴ mgh = 10 J
∴ m = \(\frac{10 \mathrm{~J}}{g h}\)
= \(\frac{10 \mathrm{~J}}{\left(10 \mathrm{~m} \mathrm{~s}^{-2}\right)(5 \mathrm{~m})}\)
= 0.2 kg
ઉત્તરઃ
D. 0.2 kg

પ્રશ્ન 24.
જ્યારે પદાર્થ પૃથ્વી તરફ મુક્ત પતન કરે છે ત્યારે તેની કુલ યાંત્રિક ઊર્જા …………..
A. વધે છે
B. ઘટે છે
C. અચળ રહે છે
D. પહેલાં વધે છે અને પછી ઘટે છે

Hint: પદાર્થની કુલ યાંત્રિક ઊર્જા
= સ્થિતિ-ઊર્જા E_p + ગતિ-ઊર્જા E_k
મુક્ત પતન કરતા પદાર્થની સ્થિતિ-ઊર્જા જેટલી ઘટે છે તેટલી જ ગતિ-ઊર્જા વધે છે.
ઉત્તરઃ
C. અચળ રહે છે

પ્રશ્ન 25.
એક પદાર્થ પર થતું કાર્ય કણ છે, તો તેના પર લાગતાં બળ અને તેના સ્થાનાંતર વચ્ચેનો ખૂણો …………… હશે.
A. 0°
B. 45°
C. 90°
D. 180°
ઉત્તરઃ
D. 180°

પ્રશ્ન 26.
10 kg દળવાળા લોખંડના ગોળાનો વ્યાસ, 3.5 kg દળવાળા ઍલ્યુમિનિયમના ગોળાના વ્યાસ જેટલો છે. એક ટાવર પરથી બંનેને એકસાથે મુક્ત પતન કરાવવામાં આવે છે. જ્યારે બંને જમીનથી 10 m ઊંચાઈએ હશે ત્યારે ………………
A. તેમનો પ્રવેગ સમાન હશે.
B. તેમનું વેગમાન સમાન હશે
C. તેમની સ્થિતિ-ઊર્જા સમાન હશે.
D. તેમની ગતિ-ઊર્જા સમાન હશે.

Hint: તેમનો પ્રવેગ ગુરુત્વપ્રવેગ ‘g’ જેટલો હશે.
ઉત્તરઃ
A. તેમનો પ્રવેગ સમાન હશે.

પ્રશ્ન 27.
એક છોકરી 3kg દળવાળી સ્કૂલ-બૅગ પોતાની પીઠ ઉપર ઊંચકીને 200 m અંતર સમક્ષિતિજ રસ્તા પર ચાલે છે, તો ગુરુત્વાકર્ષણ બળ વિરુદ્ધ થયેલું કાર્ય …………. હશે. (g = 10 m s^-2)
A. 6 × 10³ J
B. 6 J
C. 0.6 J
D. શૂન્ય
ઉત્તરઃ
D. શૂન્ય

પ્રશ્ન 28.
નીચેનામાંથી કયો એકમ ઊર્જાનો નથી?
A. joule
B. newton metre
C. kilowatt
D. kilowatt hour
ઉત્તરઃ
C. kilowatt

પ્રશ્ન 29.
પદાર્થ પર થતું કાર્ય ………… પર આધારિત નથી.
A. સ્થાનાંતર
B. લગાડેલા બળ
C. બળ અને સ્થાનાંતર વચ્ચેનો ખૂણો
D. પદાર્થના પ્રારંભિક વેગ
ઉત્તરઃ
D. પદાર્થના પ્રારંભિક વેગ

પ્રશ્ન 30.
બંધના કારણે સંગૃહીત થયેલું પાણી ……………
A. ઊર્જા ધરાવતું નથી.
B. વિદ્યુત-ઊર્જા ધરાવે છે.
C. ગતિ-ઊર્જા ધરાવે છે.
D. સ્થિતિ-ઊર્જા ધરાવે છે.
ઉત્તરઃ
D. સ્થિતિ-ઊર્જા ધરાવે છે.

પ્રશ્ન 31.
એક પદાર્થ કે ઊંચાઈએથી મુક્ત પતન કરે છે. \(\frac{h}{2}\) અંતર અધોદિશામાં કાપે ત્યારે, તે સ્થાને …………….
A. તે માત્ર સ્થિતિ-ઊર્જા ધરાવે છે.
B. તે માત્ર ગતિ-ઊર્જા ધરાવે છે.
C. તે અડધી સ્થિતિ-ઊર્જા અને અડધી ગતિ-ઊર્જા ધરાવે છે.
D. તે વધુ ગતિ-ઊર્જા અને ઓછી સ્થિતિ-ઊર્જા ધરાવે છે.
ઉત્તરઃ
C. તે અડધી સ્થિતિ-ઊર્જા અને અડધી ગતિ-ઊર્જા ધરાવે છે.

પ્રશ્ન 32.
એક છોકરો 300 g જેટલું દળ 1.2 sમાં 4m જેટલી ઊંચાઈ સુધી ઊંચકે છે. આ છોકરાનો પાવર કેટલો હશે?
A. 5 W
B. 10 W
C. 15 W
D. 20 w

Hint: P = \(\frac{W}{t}\) = \(\frac{m g h}{t}\)
= \(\frac{0.3 \times 9.8 \times 4}{1.2}\) = 9.8 W ≈ 10 W
ઉત્તરઃ
B. 10 W

પ્રશ્ન 33.

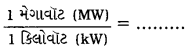
A. 10^-3
B. 10³
C. 10⁶
D. 10^-6

Hint: \(\frac{1 \mathrm{MW}}{1 \mathrm{~kW}}\) = \(\frac{10^{6} \mathrm{~W}}{10^{3} \mathrm{~W}}\) = 10³
ઉત્તરઃ
B. 10³

મૂલ્યો આધારિત પ્રશ્નોત્તર
(Value Based Questions with Answers)

પ્રશ્ન 1.
શાલિની અને વિશ્વા બંને ધોરણ 9માં અભ્યાસ કરે છે. તેમના વર્ગમાં તેમના વિજ્ઞાન વિષયના શિક્ષક કાર્ય, ઊર્જાના વિવિધ પ્રકારો અને તેમના પરસ્પર રૂપાંતરણો વિષે યોગ્ય સમજૂતી આપે છે.
શાલિની નીચે મુજબના બે પ્રશ્નો વિશ્વાને પૂછે છે:
(i) જો પદાર્થનું વેગમાન શૂન્ય હોય, તો પણ તેની કુલ યાંત્રિક ઊર્જા શૂન્ય હોતી નથી. કેમ?
(ii) જો પદાર્થની કુલ યાંત્રિક ઊર્જા શૂન્ય હોય તો તેનું વેગમાન શૂન્ય હોય છે. શા માટે?
વિશ્વા ઉપરોક્ત બંને પ્રશ્નોના સાચા ઉત્તર કારણ સહિત શાલિનીને આપે છે, તો ..
(a) વિશ્વાએ આપેલ સાચા ઉત્તરો કયા હશે?
ઉત્તર:
(i) પદાર્થની કુલ યાંત્રિક ઊર્જા એટલે તેની સ્થિતિ-ઊર્જા અને ગતિ-ઊર્જાનો સરવાળો અર્થાત્ E = E_p + E_K હવે જો પદાર્થનું વેગમાન (p = mv) શૂન્ય હોય, તો તેનો વેગ શૂન્ય હશે (∵ m ≠ 0). તેથી તેની ગતિ-ઊર્જા શૂન્ય હશે પણ પદાર્થની યાંત્રિક ઊર્જા, સ્થિતિ-ઊર્જા જેટલી હશે. તેથી યાંત્રિક ઊર્જા શૂન્ય નથી.
(ii) પદાર્થની કુલ યાંત્રિક ઊર્જા શૂન્ય હશે તો તેની ગતિ ઊર્જા E_K અને સ્થિતિ-ઊર્જા E_p બંને શૂન્ય હશે.
અત્રે, ગતિ-ઊર્જા શૂન્ય હોવાથી પદાર્થનો વેગ શૂન્ય હશે અને તેથી તેનું વેગમાન પણ શૂન્ય હશે.

(b) શાલિનીના કયા ગુણો અહીં પ્રદર્શિત થાય છે?
ઉત્તર:
(i) અભ્યાસુ સ્વભાવ
(ii) વિજ્ઞાનના મૂળભૂત સિદ્ધાંતો સમજવા માટેની જિજ્ઞાસા

(c) વિશ્વાના કયા ગુણો અહીં પ્રદર્શિત થાય છે?
ઉત્તર:
(i) કાર્ય, ઊર્જાના પ્રકારો અને તેમનાં પરસ્પર રૂપાંતરણો અંગેની ઊંડી અને સાચી સમજ
(ii) બીજાને શીખવાડવાની અને સહાયભૂત થવાની ભાવના

પ્રશ્ન 2.
વિરાજ અને વિનિત નવમા ધોરણમાં અભ્યાસ કરે છે. તેમની પડોશમાં એક ચાર માળનું મકાન છે. તે મકાનમાં ભોયતળિયાથી અગાસીમાં જવા માટે જુદા જુદા પ્રકારની બે સીડીઓ છે. એક ઢાળવાળી અને બીજી સ્વાયરલ આકારની શિરોલંબ.
અહીં બંને મિત્રોના દળ સમાન છે. વિરાજ, વિનિતને કહે છે રે કે ભોયતળિયેથી અગાસીમાં જવા માટે સ્પાયરલ આકારની શિરોલંબ
સીડીના બદલે ઢાળવાળી સીડી વાપરતા એક કુદરતી બળ વિરુદ્ધ ગતિ કરવામાં વધુ કાર્ય કરવું પડે છે, કારણ કે અંતર વધારે કાપવું પડે છે.
વિનિત, વિરાજની વાત સાથે સહમત નથી. તે જણાવે છે કે ઢાળવાળી કે સ્પાયરલ શિરોલંબ સીડી કોઈ પણ વાપરવામાં આવે તો બંને વખતે કુદરતી બળ વિરુદ્ધ એકસમાન કાર્ય જ કરવું પડે છે.
પછી વિરાજ ઢાળવાળી સીડીની મદદથી ભોયતળિયાથી અગાસીમાં 3 90 sમાં પહોંચે છે અને વિનિત સ્પાયરલ શિરોલંબ સીડી મારફતે 2 મિનિટમાં ભોયતળિયેથી અગાસીમાં પહોંચે છે, તો ….
(a) ભોયતળિયેથી અગાસીમાં જતી વખતે કયા કુદરતી બળ વિરુદ્ધ કાર્ય થાય છે?
ઉત્તર:
ગુરુત્વાકર્ષણ બળ

(b) ભોંયતળિયેથી અગાસીમાં જવા માટે કોના દ્વારા વધુ કાર્ય થાય છે? કોનો પાવર વધુ છે?
ઉત્તર:
વિરાજ અને વિનિત બંને દ્વારા એકસમાન કાર્ય થાય છે, કારણ કે બંને દ્વારા કપાયેલું ઊર્ધ્વ શિરોલંબ અંતર સમાન છે, જે બંને એકસરખું બળ વાપરીને કાપે છે.
અહીં,

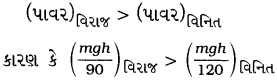
(c) વિનિતના કયા ગુણો અહીં પ્રદર્શિત થાય છે?
ઉત્તર:
વિનિતના ગુણો :
(i) ગુરુત્વાકર્ષણ બળ વિષેની સાચી અને યોગ્ય જાણકારી
(ii) ગુરુત્વાકર્ષણ બળ વિરુદ્ધ થતાં કાર્યની ગણતરી કરવા અંગેનું યથાર્થ જ્ઞાન
(iii) રોજબરોજના પ્રશ્નો / કાયદાઓ ઉકેલવા માટેની સમજણશક્તિ.

પ્રશ્ન 3.
સંજય એક શહેરમાંની એક શાળામાં ધોરણ 9માં અભ્યાસ કરે છે, જ્યાં થર્મલ પાવર સ્ટેશન દ્વારા વિજળી પૂરી પાડવામાં આવે છે છે. રાજ્ય સરકાર અચાનક તાત્કાલિક અસરથી વિજળીનો ભાવ વધારી નાખે છે. પરિણામે સંજયના કુટુંબને તે મહિનાનું વીજળીનું બિલ ઘણું વધારે આવે છે.

સંજયનું કુટુંબ આ વધુ વીજળીના બિલને કારણે ચિંતામાં મુકાઈ જાય છે. સંજય આ પ્રૉબ્લેમ વિષે ઊંડું વિચારે છે અને વીજળીનું બિલ ઘટાડવા અંગે કેટલાંક સૂચનો કરે છે.

જ્યારે આ સૂચનોનું પાલન કરવામાં આવે છે ત્યારે બીજા મહિને વીજળીનાં બિલમાં ઘટાડો જોવા મળે છે. તેથી કુટુંબનો દરેક સભ્ય ખુશ થાય છે, કારણ કે “પૈસાની બચત એટલે પૈસાની કમાણી.”
(a) થર્મલ પાવર સ્ટેશન કોને કહે છે?
ઉત્તર:
થર્મલ એટલે ઉખા
જે સ્ટેશનમાં બળતણ(દા. ત., કોલસો, કુદરતી ગૅસ)ના દહન વડે વીજળી ઉત્પન્ન કરવામાં આવતી હોય તેને થર્મલ પાવર સ્ટેશન કહે છે.

(b) સંજયે કરેલાં સૂચનો જણાવો.
ઉત્તર:
સંજયે કરેલાં સૂચનોઃ
(i) લાઇટ, પંખા, ટીવી અને બીજાં વિદ્યુત ઉપકરણોનો ઉપયોગ પૂર્ણ થયા પછી તરત જ તેમને બંધ કરી દેવાં.
(ii) પરંપરાગત ફિલામેન્ટ ધરાવતાં બલ્બની જગ્યાએ CFL (Compact Florecent Lamp) વાપરવા કારણ કે તેમના ઉપયોગથી વીજળી ઓછી વપરાય છે.
(iii) ઇલેક્ટ્રિક ગીઝરની જગ્યાએ સોલર વોટર હીટર વાપરવું.
(iv) જ્યારે શક્ય હોય ત્યારે સોલર કૂકરનો ઉપયોગ
ઇલેક્ટ્રિક સગડીની જગ્યાએ કરવો.

(c) સંજયના કયા ગુણો અહીં જોવા મળે છે?
ઉત્તર:
સંજયના ગુણોઃ
(i) વીજળીની બચત અંગેની જાણકારી અને જાગૃતતા
(ii) પર્યાવરણની જાળવણી અંગેની સભાનતા
(iii) કુટુંબ પ્રત્યેની કૃતજ્ઞતા અને વફાદારી

પ્રાયોગિક કૌશલ્ય આધારિત પ્રશ્નોત્તર
(Practical Skill Based Question with Answer)

નોંધઃ આ પ્રકરણમાંથી પ્રયોગો ફાળવાયેલા નથી. તેથી પ્રાયોગિક કૌશલ્યને લગતા પ્રશ્નોત્તર નથી.

Memory Map