Gujarat Board GSEB Solutions Class 10 Maths Chapter 10 વર્તુળ Ex 10.2 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 10 Maths Chapter 10 વર્તુળ Ex 10.2
પ્રશ્ન 1થી 3માં સાચો વિકલ્પ પસંદ કરો અને તે માટે કારણ આપો.
પ્રશ્ન 1.
બિંદુ Qમાંથી દોરેલા વર્તુળના સ્પર્શકની લંબાઈ 24 સેમી અને વર્તુળના કેન્દ્રથી તેનું અંતર 25 સેમી હોય, તો વર્તુળની ત્રિજ્યા ………………. છે.
(A) 7 સેમી
(B) 12 સેમી
(C) 15 સેમી
(D) 24.5 સેમી
ઉત્તર:
ધારો કે, વર્તુળનું કેન્દ્ર P છે તથા 9માંથી દોરેલ સ્પર્શકનું સ્પર્શબિંદુ T છે. આથી PT એ સ્પર્શબિંદુમાંથી દોરેલ ત્રિજ્યા થાય તથા PQ = 25 સેમી અને QT = 24 સેમી થાય.
∆ PTOમાં ∠T = 90° (પ્રમેય 10.1)
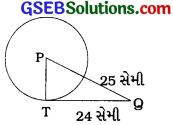
PT = \(\sqrt{\mathrm{PQ}^{2}-\mathrm{TQ}^{2}}\) (પાયથાગોરસ પ્રમેય)
PT = \(\sqrt{25^{2}-24^{2}}\)
PT = \(\sqrt{625-576}\)
PT = \(\sqrt{49}\)
PT = 7 સેમી
આમ, સાચો વિકલ્પ (A) 7 સેમી છે.

પ્રશ્ન 2.
આપેલ આકૃતિમાં, જો TP અને TQ એ છે કેન્દ્રવાળા વર્તુળના ∠POQ = 110° બને એવા સ્પર્શકો છે, તો ∠PTQ = …… છે.
(A) 60°
(B) 70°
(C) 80°
(D) 90°
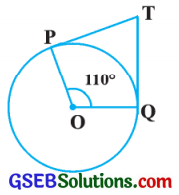
ઉત્તર:
અહીં, ચતુષ્કોણ POQTમાં,
∠P + ∠O + ∠Q + ∠T = 360°
90° + 110° + 90° + ∠T = 360° (પ્રમેય 10.1)
290° + ∠T = 360°
∠T = 70°
∠PTQ = 70°
આમ, સાચો વિકલ્પ (B) 70° છે.

પ્રશ્ન 3.
જો O કેન્દ્રવાળા વર્તુળને બિંદુ માંથી દોરેલા સ્પર્શકો PA અને PB વચ્ચે 80નો ખૂણો રચાતો હોય, તો ∠POA = ……….. છે.
(A) 50°
(B) 60°
(C) 70°
(D) 80°
ઉત્તર:
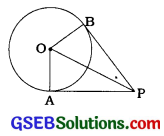
અહીં, ∠APB = 80° ચતુષ્કોણ OAPBમાં,
∠AOB + ∠OAP + ∠APB + ∠PBD = 360°
∠AOB + 90° + 80° + 90° = 360° (આપેલ અને પ્રમેય 10.1) .
∠AOB + 260° = 360°
∠AOB = 100°
હવે, OP એ ∠AOBને દુભાગે છે.
∠POA = ∠POB = \(\frac{1}{2}\) ∠AOB
∠POA = \(\frac{100^{\circ}}{2}\)
∠POA = 50°
આમ, સાચો વિકલ્પ (A) 50° છે.

પ્રશ્ન 4.
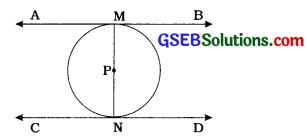
સાબિત કરો કે, વર્તુળના વ્યાસના અંત્યબિંદુઓએ દોરેલા સ્પર્શકો પરસ્પર સમાંતર હોય છે.
ઉત્તર:
પક્ષ: P કેન્દ્રવાળા વર્તુળમાં MN વ્યાસ છે. AB અને CD એ છે વર્તુળના સ્પર્શક છે, જે વર્તુળને અનુક્રમે M અને Nમાં હું સ્પર્શે છે.
સાધ્ય: AB || CD
સાબિતી: AB એ વર્તુળને M બિંદુએ સ્પર્શક છે અને PM એ છે સ્પર્શબિંદુ Mમાંથી દોરેલ ત્રિજ્યા છે.
∠PMA = 90° (પ્રમેય 10.1)
∠NMA = 90° (: MN એ વ્યાસ છે.) ……………… (1)
તે જ રીતે, CD એ વર્તુળને N બિંદુએ સ્પર્શક છે ? અને PN એ સ્પર્શબિંદુ માંથી દોરેલ ત્રિજ્યા છે. છે
∠DNP = 90° (પ્રમેય 10.1)
∠MND = 90° …………… (2)
(1) અને (2) પરથી,
∠NMA = ∠MND
પરંતુ, આ બે ખૂણાઓ રેખા AB અને CDની છેદિકા ? દ્વારા બનતા યુગ્મકોણ છે અને તેઓ સમાન છે.
∴ AB || CD

પ્રશ્ન 5.
સાબિત કરો કે, વર્તુળના સ્પર્શકના સ્પર્શબિંદુમાંથી દોરેલો લંબ રે વર્તુળના કેન્દ્રમાંથી પસાર થાય છે.
ઉત્તર:
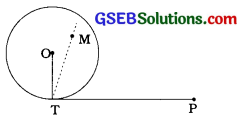
અહીં, PT એ છે કેન્દ્રવાળા વર્તુળને T. બિંદુમાં સ્પર્શતો સ્પર્શક છે અને બિંદુ M વર્તુળના અંદરના ભાગનું એવું બિંદુ છે, જેથી MT ⊥ PT થાય.
ધારો કે, TM એ કેન્દ્ર 0માંથી પસાર નથી થતી.
હવે, ∠MTP = 90° (∵ MT ⊥ PT)
વળી, ∠OTP = 90° (પ્રમેય 10.1)
∴ ∠MTP = ∠OTP
આ ત્યારે જ શક્ય થાય જ્યારે OT અને MT સંપાતી હોય. આથી MT કેન્દ્ર 0માંથી પસાર થાય છે. આમ, વર્તુળના સ્પર્શકના સ્પર્શબિંદુમાંથી દોરેલો લંબ વર્તુળના કેન્દ્રમાંથી પસાર થાય છે.

પ્રશ્ન 6.
વર્તુળના કેન્દ્રથી 5 સેમી અંતરે આવેલા બિંદુ થી દોરેલા સ્પર્શકની લંબાઈ 4 સેમી છે. વર્તુળની ત્રિજ્યા શોધો.
ઉત્તર:
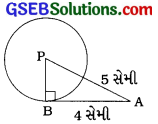
AB એ P કેન્દ્રવાળા વર્તુળનો સ્પર્શક છે અને B સ્પર્શબિંદુ છે.
આથી PA = 5 સેમી અને AB = 4 સેમી.
∆ PBAમાં, ∠B = 90° (પ્રમેય 10.1)
∴ PB = \(\sqrt{\mathrm{PA}^{2}-\mathrm{AB}^{2}}\)
= \(\sqrt{5^{2}-4^{2}}\)
= \(\sqrt{25-16}=\sqrt{9}\)
∴ PB = 3 સેમી
આમ, વર્તુળની ત્રિજ્યા 3 સેમી થાય.

પ્રશ્ન 7.
બે સમકેન્દ્રી વર્તુળોની ત્રિજ્યા 5 સેમી અને 3 સેમી છે. મોટા વર્તુળની જીવા નાના વર્તુળને સ્પર્શે છે, તો તેની લંબાઈ શોધો.
ઉત્તર:
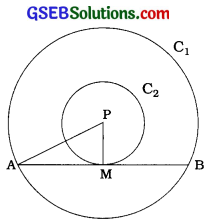
P કેન્દ્રવાળાં બે સમકેન્દ્રીય વર્તુળો C1 અને C2 માં C1 ની ત્રિજ્યા 5 સેમી અને C2 ની ત્રિજ્યા 3 સેમી છે. C1 ની જીવા AB એ C2 ને M બિંદુમાં સ્પર્શે છે.
આથી PA = 5 સેમી, PM = 3 સેમી,
∠PMA = 90° અને AB = 2AM.
∆ PMAમાં, ∠M = 90°.
∴ AM = \(\sqrt{\mathrm{PA}^{2}-\mathrm{PM}^{2}}\)
= \(\sqrt{5^{2}-3^{2}}\)
= \(\sqrt{25-9}\)
= \(\sqrt{16}\)
= 4 સેમી
હવે, AB = 2 AM = 2 × 40 સેમી = 8 સેમી
આમ, મોટા વર્તુળની જીવા કે જે નાના વર્તુળને સ્પર્શે છે તેની લંબાઈ 8 સેમી છે.

પ્રશ્ન 8.
ચતુષ્કોણ ABCD એક વર્તુળને પરિગત છે. (જુઓ આકૃતિ) સાખિત કરો, AB + CD = AD + BC.
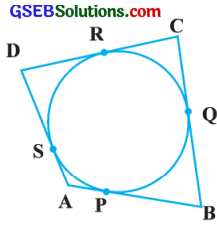
પ્રમેય 10.2 મુજબ વર્તુળની બહારના બિંદુમાંથી દોરેલા સ્પર્શકોની લંબાઈ સમાન હોય છે. આથી
AP = AS ………….(1)
BP = BQ …………(2)
CR = CQ ………….(3)
DR = DS ………….(4)
ઉપરોક્ત બધાં જ પરિણામોનો સરવાળો લેતાં,
AP + BP + CR + DR = AS + BQ + CD + DS
∴ (AP + BP) + (CR+ DR) = (AS + DS) + (BQ + CQ)
∴ AB + CD = AD + BC

પ્રશ્ન 9.
આપેલ આકૃતિમાં, o કેન્દ્રવાળા વર્તુળના બે સ્પર્શકો XY અને X’Y’ સમાંતર છે અને વર્તુળ પરના સ્પર્શબિંદુ C આગળ દોરેલો ત્રીજો સ્પર્શક XYને A બિંદુએ અને X’Y’ને B બિંદુએ છેદે છે. સાબિત કરો કે, ∠AOB = 90°.
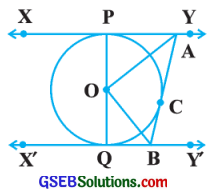
ઉત્તર:
ત્રિજ્યા OC દોરો.
અહીં, ∠OPA = ∠OCA = 90° (પ્રમેય 10.1)
AP = AC (પ્રમેય 10.2)
AO = AO (એક જ રેખાખંડ)
આથી એકરૂપતાની કાકબા શરત મુજબ,
∆ OAP ≅ ∆ OAC
∴ ∠OAP = ∠OAC (CPCT)
∴ ∠OAC = \(\frac{1}{2}\) ∠PAC …………. (1)
તે જ રીતે,
∴ ∠DOB = ∠OCB
∴ ∠OBQ = ∠OBC
∴ ∠OBC = ∠QBC ……….. (2)
(1) અને (2)નો સરવાળો લેતાં,
∠OAC + ∠OBC = \(\frac{1}{2}\) ∠PAC + \(\frac{1}{2}\) ∠QBC
∴ ∠OAB + ∠OBA = \(\frac{1}{2}\) (∠XAB + ∠XBA) ………… (3)
પરંતુ, ∠XAB અને ∠X’BA એ XY || X’Y’ની છેદિકા AB દ્વારા બનતા છેદિકાની એક જ તરફના અંતઃકોણ છે.
∠XAB + ∠XBA = 180° …………(4)
(3) અને (4) પરથી,
∠OAB + ∠OBA = \(\frac{1}{2}\) (180°) = 90°
હવે, ∆ DABમાં,
∠OAB + ∠OBA + ∠AOB = 180°
∴ 90° + ∠AOB = 180°
∴ ∠AOB = 90°

પ્રશ્ન 10.
સાબિત કરો કે, વર્તુળની બહારના બિંદુમાંથી વર્તુળને દોરેલા બે સ્પર્શકો વચ્ચેનો ખૂણો અને સ્પર્શબિંદુઓને કેન્દ્રને જોડતા રેખાખંડ વચ્ચેનો ખૂણો એકબીજાને પૂરક હોય છે.
ઉત્તર:
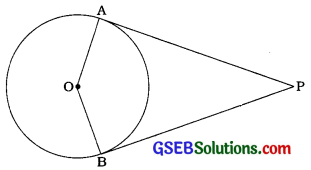
પક્ષ: બિંદુ P એ છે કેન્દ્રિત વર્તુળના બહારના ભાગનું બિંદુ છે તથા Pમાંથી દોરેલા સ્પર્શકો PA અને PB વર્તુળને અનુક્રમે A અને Bમાં સ્પર્શે છે.
સાધ્ય: ∠APB + ∠AOB = 180°
સાબિતી: PA એ છે કેન્દ્રિત વર્તુળનો સ્પર્શક છે તથા A સ્પર્શબિંદુ છે.
∴ ∠PAO = 90° (પ્રમેય 10.1)
PB એ છે કેન્દ્રિત વર્તુળનો સ્પર્શક છે તથા B સ્પર્શબિંદુ છે.
∴ ∠PBO = 90° (પ્રમેય 10.1)
હવે, ચતુષ્કોણ PAOBમાં,
∠PAO + ∠AOB + ∠PBO + ∠APB = 360°
∴ 90° + ∠AOB + 90° + ∠APB = 360°
∴ ∠APB + ∠AOB = 180°

પ્રશ્ન 11.
સાબિત કરો કે, વર્તુળને પરિગત સમાંતરબાજુ ચતુષ્કોણ સમબાજુ ચતુષ્કોણ છે.
ઉત્તર:
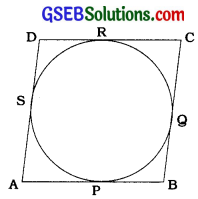
અહીં, ABCD એ એક વર્તુળને પરિગત સમાંતરબાજુ ચતુષ્કોણ છે, જેની બાજુઓ AB, BC, CD અને D વર્તુળને અનુક્રમે P, Q, R અને Sમાં સ્પર્શે છે.
∴ AP = AS, BP = BQ, CR = CO અને DR = DS
∴ AP + BP + CR + DR = AS + BQ + CQ + DS
∴ (AP + BP) + (CR + DR) = (AS + DS) + (B9 + CO)
∴ AB + CD = BC + DA ………….. (1)
હવે, ABCD એ સમાંતરબાજુ ચતુષ્કોણ છે.
AB = CD અને BC = DA …………… (2)
(1) અને (2) પરથી,
AB + AB = BC + BC
∴ 2AB = 2BC
∴ AB = BC
આમ, સમાંતરબાજુ ચતુષ્કોણ ABCDની પાસપાસેની બાજુઓ AB અને BC સમાન છે.
આથી સમાંતરબાજુ ચતુષ્કોણ ABCDની બધી જ બાજુઓ સમાન છે.
આથી સમાંતરબાજુ ચતુષ્કોણ ABCD એ સમબાજુ ચતુષ્કોણ છે.

પ્રશ્ન 12.
ત્રિકોણ ABC એ 4 સેમી ત્રિજ્યાવાળા વર્તુળને પરિગત છે. રેખાખંડ BD અને Pc એ BCનું સ્પર્શબિંદુ D આગળ અનુક્રમે 8 સેમી અને 6 સેમી લંબાઈના રેખાખંડમાં વિભાજન કરે છે. (જુઓ આકૃતિ) બાજુઓ AB અને AC શોધો.
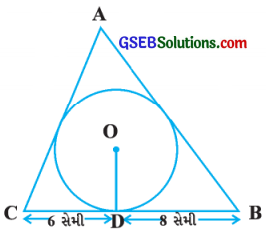
ઉત્તર:
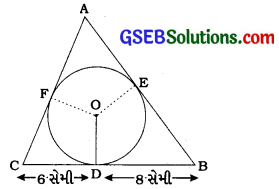
ધારો કે, AB અને AC એ ∆ ABCના અંતઃવૃત્તને અનુક્રમે E અને Fમાં સ્પર્શે છે.
આથી OD = OE = OF = r = 4 સેમી,
CD = CF = 6 સેમી અને BD = BE = 8 સેમી.
ધારો કે, AE = AF = x સેમી.
∆ ABCની પરિમિતિ = AB + BC + CA
= (AE + BE) + (BD + CD) + (CF + AF)
= (x + 2) + (8 + 6) + (6 + 1)
= (2x + 28) સેમી
∴ ABC ની અર્ધપરિમિતિ = s
= \(\frac{2 x+28}{2}\)
= (x + 14) સેમી
∆ ABCમાં, a = BC = 14 સેમી, b = AC = (x + 6) સેમી અને c = AB = (x + 8) સેમી
હવે, હેરોનના સૂત્ર મુજબ,
∆ ABCનું ક્ષેત્રફળ = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{\begin{array}{r}
(x+14)(x+14-14)(x+14-x-6) \\
(x+14-x-8)
\end{array}}\)
= \(\sqrt{x(x+14)(8)(6)}\) સેમી2 ………… (1)
વળી,
∆ ABCનું ક્ષેત્રફળ = ∆ DABનું ક્ષેત્રફળ + ∆ OBCનું ક્ષેત્રફળ + ∆ OCAનું ક્ષેત્રફળ
= \(\frac{1}{2}\) × AB × OE + \(\frac{1}{2}\) × BC × OD + \(\frac{1}{2}\) × CA × OF
= \(\frac{1}{2}\) × AB × 4 + \(\frac{1}{2}\) × BC × 4 + \(\frac{1}{2}\) × CA × 4
= 2 (AB+ BC + CA)
= 2 (2x + 28) સેમી2 ………… (2)
(1) અને (2) પરથી,
2 (2x + 28) = \(\sqrt{x(x+14)(8)(6)}\)
4 (x + 14) = 4\(\sqrt{3 x} \cdot \sqrt{x+14}\)
\(\sqrt{x+14}=\sqrt{3 x}\)
x + 14 = 3x
2x = 14
x = 7
હવે, AB = AE + BE = x + 8 = 7 + 8 = 15 સેમી
અને AC = AF + CF = x + 6 = 7 + 6 = 3 સેમી.
આમ, AB = 15 સેમી અને AC = 13 સેમી.

પ્રશ્ન 13.
સાબિત કરો કે, વર્તુળને પરિગત ચતુષ્કોણની સામસામેની ? બાજુઓથી વર્તુળના કેન્દ્ર આગળ રચાતા ખૂણાઓ પૂરક હોય છે.
ઉત્તર:
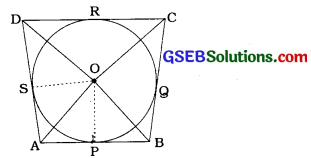
પક્ષ: ચતુષ્કોણ ABCD એ 9 કેન્દ્રિત વર્તુળને પરિગત છે તથા યતુષ્કોણ ABCDની ખાજુઓ AB, BC, CD અને DA વર્તુળને અનુક્રમે P Q R અને Sમાં સ્પર્શે છે.
સાધ્ય: ∠AOB + ∠COD = 180° અને
∠BOC + ∠DOA = 180°
સાબિતી: વર્તુળની ત્રિજ્યા OP અને OS દોરો.
∆ OAP અને ∆ OASમાં,
OA = OA (એક જ રેખાખંડ)
AP = AS (પ્રમેય 10.2)
OP = OS (એક જ વર્તુળની ત્રિજ્યાઓ)
બાબાબા મુજબ, ∆ OAP ≅ ∆ OAS
∠OAP = ∠OAS
પરંતુ, ∠OAP + ∠OAS = ∠PAS = ∠BAD
∠OAP = \(\frac{1}{2}\) ∠BAD
∠OAB = \(\frac{1}{2}\) ∠BAD ………. (1)
તે જ રીતે, ∠OBA = \(\frac{1}{2}\) ∠ABC, …… (2)
∠OCD = \(\frac{1}{2}\) ∠BCD, ………… (3)
અને ∠ODC = \(\frac{1}{2}\) ∠CDA ………. (4)
(1), (2), (3) અને (4) નો સરવાળો લેતાં,
∠OAB + ∠OBA + ∠OCD + ∠ODC = \(\frac{1}{2}\) (∠BAD + ∠ABC + ∠BCD + ∠CDA)
∠TAB + ∠OBA + ∠OCD + ∠ODC = \(\frac{1}{2}\) (360°) = 180° …………… (5)
∆ OAB અને ∆ OCDમાં,
(∠OAB + ∠OBA + ∠AOB) + (∠OCD + ∠ODC + ∠COD) = 180° + 180°
(∠AOB + ∠COD) + (∠OAB + ∠OBA + ∠OCD + ∠ODC) = 360°
∠AOB + ∠COD + 180° = 360° [(5) મુજબ]
∠AOB + ∠COD = 180°
હવે, એક બિંદુ આગળ બનતા બધા જ ખૂણાની સરવાળો 360° થાય.
∠AOB + ∠BOC + ∠COD + ∠DOA = 360°
(∠AOB + ∠COD) + (∠BOC + ∠DOA) = 360°
∴ 180° + ∠BOC +∠DOA = 360°
∴ ∠BOC + ∠DOA = 180°
આમ, વર્તુળને પરિગત ચતુષ્કોણની સામસામેની બાજુઓથી વર્તુળના કેન્દ્ર આગળ રચાતા ખૂણાઓ પૂરક હોય છે.