Gujarat Board GSEB Solutions Class 10 Maths Chapter 15 સંભાવના Ex 15.1 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 10 Maths Chapter 15 સંભાવના Ex 15.1
પ્રશ્ન 1.
નીચેના વિધાનો પૂર્ણ કરોઃ
(i) ઘટના E ની સંભાવના + ઘટના ‘E નહીં’ ની સંભાવના = ………………
જવાબઃ
1
(ii) ઉદ્ભવી ન શકે તેવી ઘટનાની સંભાવના ………….. છે. આવી ઘટનાને …………… કહે છે.
જવાબઃ
0, અશક્ય ઘટના
(iii) ચોક્કસપણે ઉદ્ભવતી ઘટનાની સંભાવના ………… છે. આવી ઘટનાને ………… કહે છે.
જવાબઃ
1, ચોક્કસ ઘટના અથવા નિશ્ચિત ઘટના
(iv) પ્રયોગની તમામ મૂળભૂત (પ્રાથમિક) ઘટનાઓની સંભાવનાઓનો સરવાળો …….. છે.
જવાબઃ
1
(v) ઘટનાની સંભાવના …થી મોટી અથવા તેના જેટલી અને એથી નાની અથવા તેના જેટલી હોય છે.
જવાબઃ
0, 1

પ્રશ્ન 2.
નીચે આપેલ પૈકી કયા પ્રયોગનાં પરિણામો સમસંભાવી છે? સમજાવો.
(i) પ્રયોગઃ ડ્રાઇવર કાર ચાલુ કરવાનો પ્રયત્ન કરે છે.
પરિણામઃ કાર ચાલુ થાય છે અથવા ચાલુ નથી થતી.
(ii) પ્રયોગઃ ખેલાડી બાસ્કેટબૉલને તાકીને મારવાનો પ્રયત્ન કરે છે.
પરિણામઃ તે બૉલને બાસ્કેટમાં નાખે છે અથવા ચૂકી જાય છે.
(iii) પ્રયોગઃ ખરા-ખોટ પ્રશ્નનો જવાબ આપવાની કસોટી આપવામાં આવી છે.
પરિણામઃ જવાબ સત્ય છે કે અસત્ય.
(iv) પ્રયોગ: બાળક જન્મે છે.
પરિણામઃ તે બાબો છે કે બેબી.
ઉત્તર:
(i) આપેલ પ્રયોગનાં પરિણામો સમસંભાવી નથી. અહીં, કારની હાલત દર્શાવી નથી. જો કાર ચાલુ હાલતમાં હોય, તો તે તરત ચાલુ થાય, પરંતુ જો કારમાં કોઈ ખરાબી હોય, તો તે ચાલુ ન પણ થાય. આથી આપેલ પ્રયોગનાં પરિણામો સમસંભાવી નથી.
(ii) આપેલ પ્રયોગનાં પરિણામો સમસંભાવી નથી. અહીં, ખેલાડી બાસ્કેટબૉલને બાસ્કેટમાં નાખે છે અથવા ચૂકી જાય છે, તેનો આધાર ખેલાડી કુશળ છે અથવા શિખાઉ છે તેના પર આધારિત છે. તે અંગેની કોઈ માહિતી પ્રશ્નમાં આપેલ ન હોવાથી આપેલ પ્રયોગનાં પરિણામો સમસંભાવી નથી.
(iii) આપેલ પ્રયોગનાં પરિણામો સમ સંભાવી છે. જ્યારે ખરા ખોટા પ્રશ્નનો જવાબ આપવામાં આવે છે, ત્યારે ફક્ત બે જ શક્યતા છે, જવાબ સત્ય હોય અથવા જવાબ અસત્ય હોય. આ પ્રકારના પ્રશ્નમાં કોઈ ગણતરી અથવા વિવરણ માંગવામાં આવતું ન હોવાથી, આપેલ પ્રયોગનાં પરિણામો સમસંભાવી છે.
(iv) આપેલ પ્રયોગનાં પરિણામો સમસંભાવી છે. જ્યારે બાળક જન્મે ત્યારે તે બાબો છે કે બેબી એ બે જ શક્યતા છે અને તે પૈકીની કોઈ શક્યતા બીજી શક્યતાથી અધિક હોય તે શક્ય નથી. આથી આપેલ પ્રયોગનાં પરિણામો સમસંભાવી છે.

પ્રશ્ન 3.
શા માટે ફૂટબૉલની રમતની શરૂઆતમાં કઈ ટુકડીને બૉલ મળવો જોઈએ તે નક્કી કરવા, સિક્કાને ઉછાળવો નિષ્પક્ષ ક્રિયા છે એવું વિચારાય છે?
ઉત્તર:
સમતોલ સિક્કાને ઉછાળવાના પ્રયોગનાં બંને પરિણામો -છાપ અને કાંટો – સમસંભાવી છે. આથી સિક્કો ઉછાળતાં છાપ આવશે કે કાંટો આવશે તેની આગાહી કરી શકાય નહીં. આથી ફૂટબૉલની રમતની શરૂઆતમાં કઈ ટુકડીને બૉલ મળવો જોઈએ તે નક્કી કરવા, સમતોલ સિક્કો ઉછાળવો તે નિષ્પક્ષ ક્રિયા છે.

પ્રશ્ન 4.
નીચેનામાંથી કયો વિકલ્પ ઘટનાની સંભાવના ન હોઈ શકે?
(A) \(\frac{2}{3}\)
(B) – 1.5
(C) 15 %
(D) 0.7
ઉત્તર:
આપણે જાણીએ છીએ કે, કોઈ પણ ઘટના E માટે, 0 ≤ P (E) ≤ 1. આમ, કોઈ પણ ઘટનાની સંભાવના પણ અથવા 1થી મોટી ન હોઈ શકે. વિકલ્પ (B) ઋણ સંખ્યા – 1.5 દર્શાવે છે. આથી સાચો વિકલ્પ (B) 1.5 છે.

પ્રશ્ન 5.
જો P (E) = 0.05 હોય, તો “ નહીં’ની સંભાવના શું છે?
ઉત્તર:
આપણે જાણીએ છીએ કે કોઈ પણ ઘટના E માટે,
P (E) + P \((\overline{\mathrm{E}})\) = 1
P \((\overline{\mathrm{E}})\) = 1 – P (E)
P \((\overline{\mathrm{E}})\) = 1 – 0.05
P \((\overline{\mathrm{E}})\) = 0.95
P (E નહીં) = 0.95
આમ, ‘E નહીં’ ની સંભાવના 0.95 હોય.

પ્રશ્ન 6.
એક થેલામાં લીંબુના સ્વાદની જ મીઠાઈઓ છે. માલિની થેલામાં જોયા વગર એક મીઠાઈ બહાર કાઢે છે. તે
(i) નારંગીના સ્વાદની મીઠાઈ હોય
(ii) લીંબુના સ્વાદની મીઠાઈ હોય તેની સંભાવના કેટલી?
ઉત્તર:
એક થેલામાં લીંબુના સ્વાદની જ મિઠાઈઓ છે. ધારો કે, પેટીમાં કુલ 7 મીઠાઈઓ છે. માટે થેલામાંથી એક મીઠાઈ પસંદ કરવાના પ્રયોગનાં કુલ પરિણામોની સંખ્યા ૧ થાય. થેલામાં ફક્ત લીંબુના સ્વાદની જ મીઠાઈઓ છે.
∴ લીંબુના સ્વાદની મીઠાઈઓની સંખ્યા = n
∴ નારંગીના સ્વાદની મીઠાઈઓની સંખ્યા = 0
(i) ધારો કે, ઘટના A: પસંદ કરેલ મીઠાઈ નારંગીના સ્વાદની
હોય. થેલામાં નારંગીના સ્વાદની 0 મીઠાઈઓ હોવાથી ઘટના A ને સાનુકૂળ પરિણામોની સંખ્યા 0 થાય.
∴ P (A) = \(\frac{0}{n}\) = 0
(ii) ધારો કે, ઘટના B: પસંદ કરેલ મીઠાઈ લીંબુના સ્વાદની હોય.
થેલામાં લીંબુના સ્વાદની 1 મીઠાઈઓ હોવાથી ઘટના Bને સાનુકૂળ પરિણામોની સંખ્યા n થાય.
∴ P (B) = \(\frac{n}{n}\) = 1
નોંધઃ
અહીં, ઘટના A એ અશક્ય ઘટના છે અને ઘટના B ચોક્કસ ઘટના છે.
∴ P (A) = 0 અને P (B) = 1

પ્રશ્ન 7.
આપેલ છે કે, 3 વિદ્યાર્થીઓના સમૂહમાં બે વિદ્યાર્થીઓનો જન્મદિવસ સમાન ન હોય તેની સંભાવના 0.992 છે. બે વિદ્યાર્થીઓનો જન્મદિવસ સમાન હોય તેની સંભાવના કેટલી?
ઉત્તર:
ધારો કે, ઘટના A: બે વિદ્યાર્થીઓના જન્મદિવસ સમાન હોય.
આથી ઘટના A: બે વિદ્યાર્થીઓનો જન્મદિવસ સમાન ન હોય.
હવે, P (A) = 0.992 (આપેલ છે.)
કોઈ પણ ઘટના A માટે,
P (A) + P \((\overline{\mathrm{A}})\) = 1
P (A) = 1 – P \((\overline{\mathrm{A}})\) = 1 – 0.992 = 0.008
આમ, બે વિદ્યાર્થીઓનો જન્મદિવસ સમાન હોય તેની સંભાવના 0.008 છે.

પ્રશ્ન 8.
એક થેલામાં 3 લાલ અને 5 કાળા દડા છે. થેલામાંથી એક દડો યાદચ્છિક રીતે કાઢવામાં આવે છે. બહાર કાઢેલ દડો
(i) લાલ હોય
(ii) લાલ ન હોય તેની સંભાવના કેટલી?
ઉત્તર:
થેલામાં રહેલ દડાની કુલ સંખ્યા = 3 + 5 = 8.
∴ થેલામાંથી એક દડો વાદચ્છિક રીતે કાઢવાના પ્રયોગનાં કુલ પરિણામોની સંખ્યા = 8.
(i) ધારો કે, ઘટના A: બહાર કાઢેલ દડો લાલ હોય. થેલામાં 3 લાલ દડા છે.
∴ ઘટના મને સાનુકૂળ પરિણામોની સંખ્યા 3 થાય.
માટે P (A) = \(\frac{3}{8}\)
(ii) ધારો કે, ઘટના B: બહાર કાઢેલ દડો લાલ ન હોય.
અહીં, ઘટના B એ ઘટના A જ છે. P (B) = P \((\overline{\mathrm{A}})\)
= 1 – P (A) = 1 – \(\frac{3}{8}\) = \(\frac{5}{8}\)

પ્રશ્ન 9.
એક પેટીમાં 5 લાલ લખોટીઓ, 8 સફેદ લખોટીઓ અને 4 લીલી લખોટીઓ છે. પેટીમાંથી એક લખોટી યાદચ્છિક રીતે બહાર કાઢવામાં આવે છે. બહાર કાઢેલ લખોટી
(i) લાલ હોય
(ii) સફેદ હોય
(iii) લીલી ન હોય તેની સંભાવના કેટલી?
ઉત્તર:
પેટીમાં રહેલ લખોટીઓની કુલ સંખ્યા = 5 + 8 + 4 = 17
∴ પેટીમાંથી એક લખોટી યાદચ્છિક રીતે બહાર કાઢવાના પ્રયોગનાં કુલ પરિણામોની સંખ્યા = 17.
(i) ધારો કે, ઘટના A:
બહાર કાઢેલ લખોટી લાલ હોય. પેટીમાં 5 લાલ લખોટીઓ છે.
∴ ઘટના મને સાનુકૂળ પરિણામોની સંખ્યા 5 થાય.
માટે P(A) = \(\frac{5}{17}\)
(ii) ધારો કે, ઘટના B:
બહાર કાઢેલ લખોટી સફેદ હોય. પેટીમાં 8 સફેદ લખોટી છે.
ઘટના Bને સાનુકૂળ પરિણામોની સંખ્યા 8 થાય.
માટે P (B) = \(\frac{8}{17}\).
(iii) ધારો કે, ઘટના C:
બહાર કાઢેલ લખોટી લીલી ન હોય. આથી ઘટના \(\overline{\mathrm{C}}\):
બહાર કાઢેલ લખોટી લીલી હોય. પેટીમાં 4 લીલી લખોટીઓ છે.
ઘટના Cને સાનુકૂળ પરિણામોની સંખ્યા 4 થાય.
માટે P (\(\overline{\mathrm{C}}\)) = 1
હવે, P (C) = 1 – P (\(\overline{\mathrm{C}}\))
= 1 – \(\frac{4}{17}\) = \(\frac{13}{17}\)

પ્રશ્ન 10.
એક ગલ્લામાં 50 p ના સો સિક્કા, 81ના પચાસ સિક્કા, ₹ 2ના વીસ સિક્કા અને ₹ 5ના દસ સિક્કા છે. જ્યારે આ ગલ્લાને ઊંધો કરવામાં આવે ત્યારે ગલ્લામાંથી કોઈ એક સિક્કો બહાર પડે, તે સમસંભાવી હોય, તો સિક્કો
(1) 50 p નો સિક્કો હશે
(2) ₹ 5 નો સિક્કો નહીં હોય તેની સંભાવના કેટલી?
ઉત્તર:
ગલ્લામાં રહેલ સિક્કાઓની કુલ સંખ્યા = 100 + 50 + 20 + 10 = 180
∴ ગલ્લામાંથી એક સિક્કો બહાર પડે તે પ્રયોગનાં કુલ પરિણામોની સંખ્યા = 180
(i) ધારો કે, ઘટના A:
બહાર પડેલ સિક્કો 50 p નો
સિક્કો છે. ગલ્લામાં 50 p ના 100 સિક્કા છે.
∴ ઘટના મને સાનુકૂળ પરિણામોની સંખ્યા 100 થાય.
માટે P (A) = \(\frac{100}{180}=\frac{5}{9}\)
(ii) ધારો કે, ઘટના B:
બહાર પડેલ સિક્કા ₹ 5 નો સિક્કો નથી.
આથી ઘટના \(\overline{\mathrm{B}}\): બહાર પડેલ સિક્કો ૪ 5નો સિક્કો છે.
ગલ્લામાં ₹ 5ના 10 સિક્કા છે.
∴ ઘટના \(\overline{\mathrm{B}}\) ને સાનુકૂળ પરિણામોની સંખ્યા 10 થાય.
માટે P (B) = \(\frac{10}{180}=\frac{1}{18}\)
હવે, P (B) = 1 – P (\(\overline{\mathrm{B}}\))
= 1 – \(\frac{1}{18}\) = \(\frac{17}{18}\).

પ્રશ્ન 11.
ગોપી પોતાના માછલીઘર માટે દુકાનમાંથી માછલી ખરીદે છે. દુકાનદાર મોટી ટાંકીમાંથી યાદચ્છિક રીતે એક માછલી બહાર કાઢે છે. આ ટાંકીમાં 5 નર માછલી અને 8 માદા માછલી (જુઓ આકૃતિ) છે. બહાર કાઢેલ માછલી નર માછલી હોય તેની સંભાવના કેટલી?
ઉત્તર:
મોટી ટાંકીમાં રહેલી માછલીઓની કુલ સંખ્યા = 5 + 8 = 13
∴ મોટી ટાંકીમાંથી એક માછલી બહાર કાઢવાના પ્રયોગનાં કુલ પરિણામોની સંખ્યા = 13
ધારો કે, ઘટના A:
બહાર કાઢેલ માછલી નર માછલી છે. મોટી ટાંકીમાં 5 નર માછલી છે.
∴ ઘટના મને સાનુકૂળ પરિણામોની સંખ્યા 5 થાય.
∴ P (A) = \(\frac{5}{13}\)

પ્રશ્ન 12.
તકની એક રમતમાં ગોળ ફરતું એક તીર (Arrow) હોય છે. તે 1, 2, 3, 4, 5, 6, 7, 17 8માંથી કોઈ એક સંખ્યા પાસે નિર્દેશ કરતું અટકે છે (જુઓ 6 આકૃતિ) અને આ સમસંભાવી પરિણામો છે.
(i) તે 8 તરફ નિર્દેશ કરે તેની સંભાવના કેટલી?
(ii) અયુગ્મ સંખ્યા તરફ નિર્દેશ કરે તેની સંભાવના કેટલી?
(iii) 2 કરતાં મોટી સંખ્યા તરફ નિર્દેશ કરે તેની સંભાવના કેટલી?
(iv) 9 કરતાં નાની સંખ્યા તરફ નિર્દેશ કરે તેની સંભાવના કેટલી?
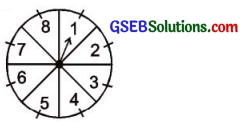
ઉત્તર:
પાટિયા પર કુલ 8 સંખ્યા છે અને ગોળ ફરતું તીર આ 8 સંખ્યા પૈકી કોઈ પાસે નિર્દેશ કરતું અટકી શકે છે.
∴ તકની રમતનાં કુલ પરિણામોની સંખ્યા = 8
(i) ધારો કે, ઘટના A:
તીર 8 તરફ નિર્દેશ કરે છે. પાટિયા પર ફક્ત એક જ 8 છે.
∴ ઘટના મને સાનુકૂળ પરિણામોની સંખ્યા 1 થાય.
∴ P (A) = \(\frac{1}{8}\).
(ii) ધારો કે, ઘટના B:
તીર અયુગ્મ સંખ્યા તરફ નિર્દેશ કરે છે. પાટિયા પર 1, 3, 5, 7 એમ 4 અયુગ્મ સંખ્યાઓ છે.
∴ ઘટના Bને સાનુકૂળ પરિણામોની સંખ્યા 4 થાય.
∴ P (B) = \(\frac{4}{8}=\frac{1}{2}\)
(iii) ધારો કે, ઘટના C:
તીર 2 કરતાં મોટી સંખ્યા તરફ નિર્દેશ કરે છે.
પાટિયા પર 2 કરતાં મોટી હોય તેવી 6 સંખ્યાઓ (3, 4, 5, 6, 7, 8) છે.
∴ ઘટના Cને સાનુકૂળ પરિણામોની સંખ્યા 6 થાય.
∴ P (C) = \(\frac{6}{8}=\frac{3}{4}\)
(iv) ધારો કે, ઘટના D:
તીર 9 કરતાં નાની સંખ્યા તરફ નિર્દેશ કરે છે.
પાટિયા પરની બધી જ 8 સંખ્યાઓ 9 કરતાં નાની છે.
∴ ઘટના સ્થળે સાનુકૂળ પરિણામોની સંખ્યા 8 થાય.
∴ P (D) = \(\frac{8}{8}\) = 1

પ્રશ્ન 13.
પાસાને એક વાર ફેંકવામાં આવે છે, તો
(i) અવિભાજ્ય સંખ્યા
(ii) 2 અને 6 વચ્ચેની સંખ્યા
(iii) અયુગ્મ સંખ્યા મળવાની સંભાવના શોધો.
ઉત્તર:
પાસાને એક વાર ફેંકવાના પ્રયોગમાં સમસંભાવી પરિણામોની સંખ્યા 6 છે.
∴ પાસાને એક વાર ફેંકવાના પ્રયોગમાં કુલ પરિણામોની સંખ્યા = 6.
(i) ધારો કે, ઘટના A:
અવિભાજ્ય સંખ્યા મળે છે. પાસા પર ત્રણ અવિભાજ્ય સંખ્યાઓ (2, 3, 5) હોય છે.
∴ ઘટના મને સાનુકૂળ પરિણામોની સંખ્યા 3 થાય.
∴ P (A) = \(\frac{3}{6}=\frac{1}{2}\)
(ii) ધારો કે, ઘટના B:
2 અને 6 વચ્ચેની સંખ્યા મળે છે. પાસા પર 2 અને 6ની વચ્ચેની ત્રણ સંખ્યાઓ (3, 4, 5) હોય છે.
∴ ઘટના Bને સાનુકૂળ પરિણામોની સંખ્યા 3 છે.
∴ P (B) = \(\frac{3}{6}=\frac{1}{2}\)
(iii) ધારો કે, ઘટના C: અયુગ્મ સંખ્યા મળે છે.
પાસા પર ત્રણ અયુગ્મ સંખ્યાઓ (1, 3, 5) હોય છે.
∴ ઘટના Cને સાનુકૂળ પરિણામોની સંખ્યા 3 છે.
∴ P (C) = \(\frac{3}{6}=\frac{1}{2}\).

પ્રશ્ન 14.
સરખી રીતે ચીપેલાં 52 પત્તાંની થોકડીમાંથી એક પતું કાઢવામાં આવે છે, તો
(i) લાલ રંગનો રાજા
(ii) મુખમુદ્રાવાળું પતું
(iii) લાલ રંગનું મુખમુદ્રાવાળું પતું
(iv) લાલનો ગુલામ
(v) કાળીનું પતું
(vi) ચોક્ટની રાણી મળવાની સંભાવના શોધો. સરખી રીતે ચીપેલાં 52 પત્તાની થોકડીમાંથી એક પતું કાઢવામાં આવે છે.
ઉત્તર:
∴ આપેલ પ્રયોગના સમસંભાવી કુલ પરિણામોની સંખ્યા = 52
(i) ધારો કે, ઘટના A:
લાલ રંગનો રાજા મળે છે. થોકડીમાં લાલ રંગના બે રાજા હોય છે. લાલનો રાજા અને ચોકટનો રાજા.
∴ ઘટના મને સાનુકૂળ પરિણામોની સંખ્યા 2 છે.
∴ P (A) = \(\frac{2}{52}=\frac{1}{26}\)
(ii) ધારો કે, ઘટના B: મુખમુદ્રાવાળું પતું મળે છે.
થોકડીમાં મુખમુદ્રાવાળાં 12 પત્તાં હોય છે. ચાર રાજા, ચાર રાણી અને ચાર ગુલામ.
∴ ઘટના B ને સાનુકૂળ પરિણામોની સંખ્યા 12 છે.
∴ P (B) = \(\frac{12}{52}=\frac{3}{13}\)
(iii) ધારો કે, ઘટના C:
લાલ રંગનું મુખમુદ્રાવાળું પતું મળે છે.
થોકડીમાં લાલ રંગના મુખમુદ્રાવાળાં 6 પત્તાં હોય છેઃ લાલ અને ચોકટ દરેકના રાજા, રાણી અને ગુલામ.
∴ ઘટના Cને સાનુકૂળ પરિણામોની સંખ્યા 6 છે.
∴ P (C) = \(\frac{6}{52}=\frac{3}{26}\)

(iv) ધારો કે, ઘટના D:
લાલનો ગુલામ મળે છે.
થોકડીમાં લાલનો ગુલામ ફક્ત એક જ હોય છે.
∴ ઘટના સ્થળે સાનુકૂળ પરિણામોની સંખ્યા 1 છે.
∴ P (D) = \(\frac{1}{52}\)
(v) ધારો કે, ઘટના E:
કાળીનું પતું મળે છે. થોકડીમાં કાળીનાં પત્તાં 13 હોય છે.
∴ ઘટના મને સાનુકૂળ પરિણામોની સંખ્યા 13 છે.
∴ P (E) = \(\frac{13}{52}=\frac{1}{4}\)
(vi) ધારો કે, ઘટના :
ચોકટની રાણી મળે છે. થોકડીમાં ચોકટની રાણી ફક્ત એક જ હોય છે.
∴ ઘટના ને સાનુકૂળ પરિણામોની સંખ્યા 1 છે.
∴ P (F) = \(\frac{1}{52}\)

પ્રશ્ન 15.
પાંચ ચોકટનાં પત્તાં – દસ્સો, ગુલામ, રાણી, રાજા અને એક્કો એ તમામના મુખ નીચે તરફ રાખીને સરખી રીતે ચિપેલાં છે, પછી એક પતું યાદચ્છિક રીતે ખેચવામાં આવે છે.
(i) પતું રાણીનું હશે તેની સંભાવના શું છે?
(ii) જો રાણીને કાઢીને એક બાજુએ મૂકવામાં આવે અને બીજું પતું ખેંચવામાં આવે તે
(a) એક્કો હોય
(b) રાણી હોય તેની સંભાવના કેટલી?
ઉત્તર:
આપેલ પ્રયોગમાં ચોટનાં પાંચ પત્તાં સરખી રીતે ચીપેલાં છે અને પછી એક પનું યાદચ્છિક રીતે ખેંચવામાં આવે છે.
∴ પ્રયોગનાં કુલ શક્ય પરિણામોની સંખ્યા = 5
(i) ધારો કે, ઘટના A:
ખેંચેલું પતું રાણીનું છે.
આપેલ પાંચ પત્તાં પૈકી રાણીનું પતું એક જ છે.
∴ ઘટના મને સાનુકૂળ પરિણામોની સંખ્યા 1 છે.
∴ P (A) = \(\frac{1}{5}\)
(ii) જો રાણીને કાઢીને એક બાજુએ મૂકવામાં આવે, તો ચાર પત્તાં બાકી રહે- દસ્સો, ગુલામ, રાજા અને એક્કો. હવે, એક પતું યાદચ્છિક રીતે ખેંચવાના પ્રયોગમાં કુલ પરિણામોની સંખ્યા 4 થાય.
(a) ધારો કે, ઘટના B:
ખેંચેલું પતું એક્કો હોય.
પ્રયોગમાં રહેલાં ચાર પત્તામાં એક્કો ફક્ત એક જ છે. – ઘટના Bને સાનુકૂળ પરિણામોની સંખ્યા 1 છે.
∴ P (B) = \(\frac{1}{4}\)
(b) ધારો કે, ઘટના C:
ખેંચેલું પતું રાણી હોય.
પ્રયોગમાં રહેલાં ચાર પત્તામાં એક પણ રાણી નથી.
∴ ઘટના Cને સાનુકૂળ પરિણામોની સંખ્યા ૦ છે.
∴ P (C) = \(\frac{0}{4}\) = 0

પ્રશ્ન 16.
ખામીવાળી 12 પેન આકસ્મિક રીતે 132 સારી પેનની સાથે ભળી ગઈ છે. એવું શક્ય નથી કે કેવળ પેનને જોઈને જ કહી શકાય કે પેન ખામીયુક્ત છે કે નહીં. આ જથ્થામાંથી એક પેન યાદચ્છિક રીતે કાઢવામાં આવે છે. કાઢવામાં આવેલી પેન ખામી રહિત છે, તેની સંભાવના શોધો.
ઉત્તર:
જથ્થામાં રહેલ કુલ પેનની સંખ્યા = 132 + 12 = 144 આ જથ્થામાંથી એક પેન યાદચ્છિક રીતે કાઢવામાં આવે છે.
∴ એક પેન કાઢવાના પ્રયોગમાં કુલ શક્ય પરિણામોની સંખ્યા = 144
ધારો કે, ઘટના A: કાઢવામાં આવેલ પેન ખામી રહિત છે.
જથ્થામાં ખામી રહિત પેનની સંખ્યા 132 છે.
∴ ઘટના મને સાનુકૂળ પરિણામોની સંખ્યા 132 છે.
∴ P (A) = \(\frac{132}{144}=\frac{11}{12}\)

પ્રશ્ન 17.
(i) 20 વીજળીના ગોળાઓનો જથ્થો 4ખામીયુક્ત ગોળા ધરાવે છે. આ જથ્થામાંથી એક ગોળો યાદચ્છિક રીતે કાઢવામાં આવે છે. આ ગોળો ખામીયુક્ત હોય તેની સંભાવના કેટલી?
(ii) ધારો કે (i)માં, કાઢવામાં આવેલ ગોળો ખામીયુક્ત નથી અને તેને પાછો મૂકવામાં પણ નથી આવ્યો. હવે, બાકીના ગોળામાંથી એક ગોળો યાદચ્છિક રીતે કાઢવામાં આવે છે. આ ગોળો ખામીયુક્ત ન હોય તેની સંભાવના કેટલી?
ઉત્તર:
(i) જથ્થામાં રહેલ ગોળાઓની કુલ સંખ્યા = 20
ખામીયુક્ત ગોળાઓની સંખ્યા = 4
∴ ખામી રહિત ગોળાઓની કુલ સંખ્યા = 20 – 4 = 16
જથ્થામાંથી એક ગોળો યાચ્છિક રીતે કાઢવામાં આવે છે.
∴ એક ગોળો યાદચ્છિક રીતે કાઢવાના પ્રયોગનાં કુલ પરિણામોની સંખ્યા = 20
ધારો કે, ઘટના A:
કાઢેલ ગોળો ખામીયુક્ત છે.
જથ્થામાં કુલ 4 ગોળા ખામીયુક્ત છે.
∴ ઘટના મને સાનુકૂળ પરિણામોની સંખ્યા 4 છે.
∴ P (A) = \(\frac{4}{20}=\frac{1}{5}\)
(ii) ધારો કે, આપેલ માહિતી મુજબ, (1)માં કાઢેલ ગોળો ખામીયુક્ત નથી (ખામી રહિત છે, અને તેને પાછો મૂકવામાં નથી આવ્યો.
આથી હવે જથ્થામાં 15 ખામી રહિત અને 4 ખામીયુક્ત એમ કુલ 19 ગોળા છે.
∴ એક ગોળો યાદચ્છિક રીતે કાઢવાના પ્રયોગનાં કુલ પરિણામોની સંખ્યા = 19.
ધારો કે, ઘટના B: કાઢેલ ગોળો ખામીયુક્ત નથી. એટલે કે, ખામી રહિત છે.
જથ્થામાં હવે 15 ગોળા ખામી રહિત છે.
∴ ઘટના Bને સાનુકૂળ પરિણામોની સંખ્યા 15 છે.
∴ P (B) = \(\frac{15}{19}\)

પ્રશ્ન 18.
એક ખોખામાં 1થી 90 સુધીની સંખ્યાઓ લખેલી 90 ગોળ તકતીઓ છે. જો ખોખામાંથી એક ગોળ તકતી યાદચ્છિક રીતે કાઢવામાં આવે તો તેના પર
(i) બે અંકની સંખ્યા,
(ii) પૂર્ણવર્ગ સંખ્યા
(iii) 5 વડે વિભાજ્ય સંખ્યા હોય તેની સંભાવના શોધો.
ઉત્તર:
1થી 90 સુધીની સંખ્યાઓ લખેલી 90 તકતીઓ જે ખોખામાં ભરેલી છે, તેમાંથી એક તકતી યાદચ્છિક રીતે કાઢવામાં આવે છે.
∴ 1 તકતી કાઢવાના પ્રયોગનાં કુલ પરિણામોની સંખ્યા = 90
(i) ધારો કે, ઘટના A:
કાઢેલી તકતી પર બે અંકની સંખ્યા હોય.
1થી 90 સુધીની સંખ્યામાં બે અંકની 81 સંખ્યાઓ છે: 10, 11, ………………., 90.
ઘટના બને સાનુકૂળ પરિણામોની સંખ્યા 8ા છે.
∴ P (A) = \(\frac{81}{90}=\frac{9}{10}\)
(ii) ધારો કે, ઘટના B:
કાઢેલી તકતી પર પૂર્ણવર્ગ સંખ્યા હોય.
1થી 90 સુધીની સંખ્યામાં પૂર્ણવર્ગ સંખ્યાઓ 9 છે: 1, 4, 9, 16, 25, 36, 49, 64, 81.
∴ ઘટના Bને સાનુકૂળ પરિણામોની સંખ્યા 9 છે.
∴ P (B) = \(\frac{9}{90}=\frac{1}{10}\)
(iii) ધારો કે, ઘટના C:
કાઢેલી તકતી પર 3 વડે વિભાજ્ય સંખ્યા હોય.
1થી 90 સુધીની સંખ્યામાં 5 વડે વિભાજ્ય હોય તેવી 18 સંખ્યાઓ છે : 5, 10, 15, …, 85, 90.
ઘટના Cને સાનુકૂળ પરિણામોની સંખ્યા 18 છે.
∴ P (C) = \(\frac{18}{90}=\frac{1}{5}\)

પ્રશ્ન 19.
એક બાળક પાસે એક એવો પાસો છે, જેની છ સપાટીઓ નીચે આપેલા અક્ષરો બતાવે છે:
![]()
આ પાસાને એક વાર ઉછાળવામાં આવે છે, પાસા પર (i) Aમળે (ii) D મળે તેની સંભાવના કેટલી?
ઉત્તર:
પાસાને એક વાર ઉછાળવામાં આવે તો તેની છ સપાટીઓ પૈકી કોઈ પણ એક સપાટી મળે.
પાસો ઉછાળવાના પ્રયોગમાં કુલ શક્ય પરિણામોની સંખ્યા = 6.
(i) ધારો કે, ઘટના X:
પાસા પર બાળકને ત મળે છે. પાસાની બે સપાટીઓ અક્ષર A બતાવે છે.
ઘટના ને સાનુકૂળ પરિણામોની સંખ્યા 2 છે.
∴ P (X) = \(\frac{2}{6}=\frac{1}{3}\)
(ii) ધારો કે, ઘટના Y:
પાસા પર બાળકને D મળે છે. પાસાની એક સપાટી અક્ષર D બતાવે છે.
∴ ઘટના ને સાનુકૂળ પરિણામોની સંખ્યા 1 છે.
∴ P (Y) = \(\frac{1}{6}\)

પ્રશ્ન 20.
ધારો કે, એક પાસાને તમે યાદચ્છિક રીતે આપેલ આકૃતિમાં બતાવ્યા પ્રમાણે લંબચોરસ ક્ષેત્ર પર ફેકો છો. તે 1 મી વ્યાસના વર્તુળની અંદર પડશે તેની સંભાવના કેટલી?
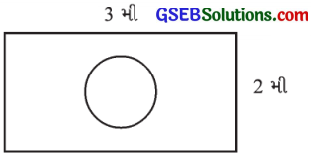
ઉત્તર:
પાસો લંબચોરસ ક્ષેત્રમાં કોઈ પણ સ્થળે પડે તે સમસંભાવી ઘટના છે.
પાસો જે લંબચોરસ ક્ષેત્રમાં પડે છે તે
લંબચોરસનું ક્ષેત્રફળ = (3 × 2) મી2
= 6 મી2
વર્તુળનું ક્ષેત્રફળ = πr2
= π(\(\frac{1}{2}\))2 મી2 (વ્યાસ = 1 મી)
= \(\frac{\pi}{4}\) મી2
માટે P (પાસો વર્તુળની અંદર પડશે) = \(\frac{\left(\frac{\pi}{4}\right)}{6}\)
= \(\frac{\pi}{24}\)

પ્રશ્ન 21.
એક જથ્થો 144 બૉલપેન ધરાવે છે. તેમાંથી 20 ખામીયુક્ત અને બાકીની સારી છે. જો પેને સારી હશે, તો નૂરી પેન ખરીદશે, પરંતુ જો તે ખામીયુક્ત હશે તો ખરીદશે નહીં. દુકાનદાર યાદચ્છિક રીતે એક પેન કાઢે છે અને તેને આપે છે.
(i) તે પેન ખરીદશે તેની સંભાવના કેટલી?
(ii) તે પેન નહીં ખરીદે તેની સંભાવના કેટલી?
ઉત્તર:
જથ્થામાં કુલ 144 પેન છે. જેમાંની 20 પેન ખામીયુક્ત છે.
∴ સારી પેનની સંખ્યા = 144 – 20 = 124
દુકાનદાર 144 પેનના જથ્થામાંથી એક પેન યાદચ્છિક રીતે કાઢે છે.
∴ એક પેન કાઢવાના પ્રયોગનાં કુલ શક્ય પરિણામોની સંખ્યા = 144.
(i) ધારો કે, ઘટના A:
નૂરી પેન ખરીદશે. પેન સારી હશે, તો જ નૂરી પેન ખરીદશે. સારી પેનની સંખ્યા 124 છે.
∴ ઘટના A ને સાનુકૂળ પરિણામોની સંખ્યા 124 છે.
∴ P (A) = \(\frac{124}{144}=\frac{31}{36}\)
(ii) ધારો કે, ઘટના B: નૂરી પેન નહીં ખરીદે.
પેન ખામીયુક્ત હશે, તો નૂરી પેન નહીં ખરીદે. ખામીયુક્ત પેનની સંખ્યા 20 છે.
ઘટના Bને સાનુકૂળ પરિણામોની સંખ્યા 20 છે.
∴ P (B) = \(\frac{20}{144}=\frac{5}{36}\)
નોંધઃ
અહીં, ઘટના B એ ઘટના Aની પૂરક ઘટના છે.
એટલે કે, B = \(\overline{\mathrm{A}}\).
આથી P (B) = P (\(\overline{\mathrm{A}}\)) = 1 – P (A)
= 1 – \(\frac{31}{36}\)
= \(\frac{5}{36}\)

પ્રશ્ન 22.
ઉદાહરણ 13ના સંદર્ભમાં (i) નીચે આપેલ કોષ્ટક પૂરું કરો:

(ii) એક વિદ્યાર્થી દલીલ કરે છે કે, 1 શક્ય પરિણામો 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 અને 12 છે. તેમાંના પ્રત્યેકની સંભાવના \(\frac{1}{11}\) છે. શું આપ આ દલીલ સાથે સહમત છો? તમારા જવાબનું સમર્થન કરો.
ઉત્તર:
(1) કુલ પરિણામોની સંખ્યા = 6 × 6 = 36.
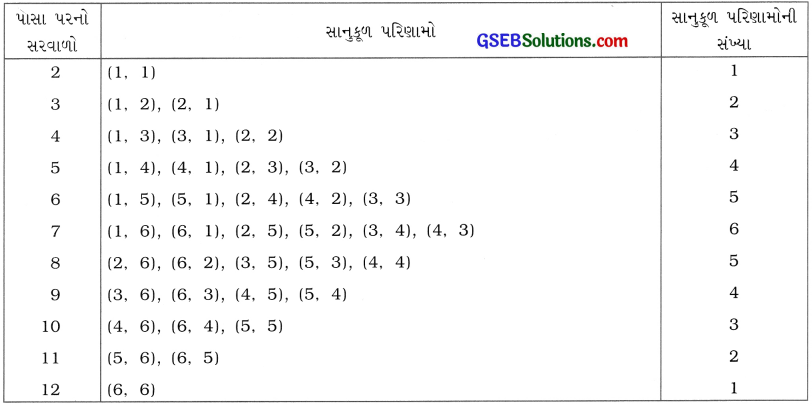

(ii) ના, વિદ્યાર્થીની દલીલ સાચી નથી. પ્રથમ તો, પાસા પરનો સરવાળો 2, 3, 4, .., 12 હોવો એ પ્રાથમિક ઘટનાઓ (પરિણામો) નથી, પરંતુ ઘટનાઓ છે. હકીકતમાં, આ પ્રયોગની પ્રાથમિક ઘટનાઓની (પરિણામો) સંખ્યા 36 છે. વધુમાં, પ્રયોગની 36 પ્રાથમિક ઘટનાઓ સમસંભાવી હોવા છતાં, 1 ઘટનાઓ પૈકીની બધી જ ઘટનાઓ સમસંભાવી નથી.

પ્રશ્ન 23.
એક રમતમાં એક રૂપિયાના સિક્કાને 3 વાર ઉછાળવાનો છે અને તેના પરિણામ દરેક વખતે નોંધવાના છે. જો તમામ વખત સિક્કો ઉછાળતાં સરખું પરિણામ મળે, એટલે કે ત્રણ છાપ અથવા ત્રણ કાંટા, તો હનિફ રમત જીતી જાય છે અન્યથા હારે છે, તો હનિફ રમત હારે તેની સંભાવનાની ગણતરી કરો.
ઉત્તર:
એક રૂપિયાના સિક્કાને એક વાર ઉછાળવાના પ્રયોગમાં ફક્ત બે પરિણામો મળે છે: છાપ (H) અને કાંટો (T).
એક રૂપિયાના સિક્કાને ત્રણ વખત ઉછાળવાના પ્રયોગમાં આપણને છાપ-છાપકાંટો જેવાં જુદાં જુદાં પરિણામો મળે છે.
છાપ-છાપ-કાંટોને આપણે HHT વડે દર્શાવીએ.
હવે, એક રૂપિયાના સિક્કાને ત્રણ વખત ઉછાળવાના પ્રયોગનાં બધાં જ શક્ય પરિણામોને આપણે નીચે મુજબ નોંધી શકીએ:
બધી જ છાપ : HHH
બે છાપ : HHT, HTH, THH
એક છાપ : HTT, THT, TTH
એક પણ છાપ નહીં (બધા જ કાંટા) : TTT
∴ એક રૂપિયાના સિક્કાને ત્રણ વખત ઉછાળવાના પ્રયોગનાં કુલ પરિણામોની સંખ્યા = 8.
ધારો કે, ઘટના A: હનિફ રમત હારે છે.
અહીં, ત્રણેય વખત સરખું પરિણામ ન મળે તેવાં 6 પરિણામો છે : HHT, HTH, THH, HTT, THT, TTH.
∴ ઘટના A ને સાનુકૂળ પરિણામોની સંખ્યા 6 છે.
∴ P (A) = \(\frac{6}{8}=\frac{3}{4}\)
નોંધ:
અહીં, P (જીત) = \(\frac{2}{8}=\frac{1}{4}\) શોધ્યા બાદ
P (હાર) = 1 – P (જીત) = 1 – \(\frac{1}{4}=\frac{3}{4}\) ની રીતે પણ ગણી શકાય.

પ્રશ્ન 24.
પાસાને બે વખત ઉછાળવામાં આવે છે.
(i) એક પણ વખત ઉપરના પૃષ્ઠ પર 5 મળે નહીં.
(ii) ઓછામાં ઓછી એક વાર ઉપરના પૃષ્ઠ પર 5 મળે તેની સંભાવના કેટલી?
સૂચનઃ એક પાસાને બે વાર ઉછાળવો અને બે પાસાને એક સાથે ઉછાળવા, એ બંનેને એક જ પ્રયોગ ગણવામાં આવે છે.]
ઉત્તર:
એક પાસાને બે વાર ઉછાળવો અને બે પાસાને એકસાથે ઉછાળવા, એ બંને એક જ પ્રયોગ થાય. ફક્ત તે બેમાં સાંકેતિક રજૂઆતના અર્થ જુદા થાય. જેમ કે, એક પાસાને બે વાર ઉછાળવાના પ્રયોગમાં (1, 1)નો અર્થ એમ થાય કે, બંને વખત પાસા પર 1 મળે છે, પરંતુ બે પાસાને એક વાર ઉછાળવાના પ્રયોગમાં (1, 1)નો અર્થ એમ થાય કે બંને પાસા પર 1 મળે છે.
∴ એક પાસાને બે વખત ઉછાળવાના પ્રયોગનાં કુલ પરિણામોની સંખ્યા = 36.
(i) ધારો કે, ઘટના A: એક પણ વખત ઉપરના પૃષ્ઠ પર 5 મળે નહીં.
ઓછામાં ઓછો એક વખત 5 આવે તેવાં 11 પરિણામો છે : (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (1, 5), (2, 5), (3, 5), (4, 5), (6, 5).
માટે બાકીનાં 25 (36 – 11) પરિણામોમાં એક પણ વખત ઉપરના પૃષ્ઠ પર 5 નહીં મળે. .
∴ ઘટના A ને સાનુકૂળ પરિણામોની સંખ્યા 25 છે.
∴ P (A) = \(\frac{25}{36}\)
(ii) ધારો કે, ઘટના B:
ઓછામાં ઓછી એક વાર ઉપરના
પૃષ્ઠ પર 5 મળે. ભાગ (1) માં દર્શાવ્યા મુજબ, એવાં 11 પરિણામો છે. જેમાં ઓછામાં ઓછી એક વાર ઉપરના પૃષ્ઠ પર 5 આવે છે.
∴ ઘટના B ને સાનુકૂળ પરિણામોની સંખ્યા 11 છે.
∴ P (B) = \(\frac{11}{36}\)
બીજી રીતે, અહીં ઘટના B એ ઘટના A ની પૂરક ઘટના છે.
એટલે કે, B = \(\overline{\mathrm{A}}\)
P (B) = P (\(\overline{\mathrm{A}}\)) = 1 – P (A)
= 1 – \(\frac{25}{36}\) = \(\frac{11}{36}\)

પ્રશ્ન 25.
નીચેનામાંથી કઈ દલીલો સાચી છે અને કઈ સાચી નથી? તમારા જવાબ માટે કારણો આપોઃ
(i) જો બે સિક્કાને એકસાથે ઉછાળવામાં આવે, તો ત્રણ શક્યતાઓ મળે છે – બે છાપ અથવા બે કાંટા અથવા પ્રત્યેકનો એક. તેથી આ પ્રત્યેક પરિણામની સંભાવના \(\frac{1}{3}\) છે.
(ii) જો પાસાને ઉછાળવામાં આવે, તો બે શક્ય પરિણામો મળે છે યુગ્મ સંખ્યા અથવા યુગ્મ સંખ્યા. તેથી અયુગ્મ સંખ્યા મળવાની સંભાવના \(\frac{1}{2}\) છે.
ઉત્તર:
(i) આપેલ દલીલ સાચી નથી. જ્યારે બે સિક્કાને એકસાથે ઉછાળવામાં આવે ત્યારે ત્રણ ઘટનાઓ મળે છે, પરંતુ પરિણામો ચાર મળે છે. કારણ કે, ઘટના “છાપ અને કાંટો બંને એક-એક બે પરિણામો HT અને TH દ્વારા બને છે. આથી ઘટનાઓ ‘બે છાપ’, બે કાંટા’ અને ‘એક છાપ તથા એક કાંટો’ની સંભાવના અનુક્રમે \(\frac{1}{4}\), \(\frac{1}{4}\) અને \(\frac{1}{2}\) મળે છે.
(ii) આપેલ દલીલ સાચી છે. જો પાસાને એક વખત ઉછાળવામાં આવે, તો જ શક્ય પરિણામો 1, 2, 3, 4, 5 અને 6 મળે છે. હવે, તે પરિણામો પૈકી ત્રણ પરિણામો અયુગ્મ સંખ્યા 1, 3, 5 બતાવે છે, જ્યારે બાકીનાં ત્રણ પરિણામો યુગ્મ સંખ્યા 2, 4, 6 બતાવે છે. આથી અયુગ્મ સંખ્યા મળવાની સંભાવના \(\frac{3}{6}=\frac{1}{2}\) થાય.