Gujarat Board GSEB Solutions Class 10 Maths Chapter 3 દ્વિચલ સુરેખ સમીકરણયુગ્મ Ex 3.2 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 10 Maths Chapter 3 દ્વિચલ સુરેખ સમીકરણયુગ્મ Ex 3.2
પ્રશ્ન 1.
નીચેની સમસ્યાઓ પરથી સુરેખ સમીકરણયુગ્મ બનાવો અને તેમનો ઉકેલ આલેખની રીતે શોધો:
(i) ધોરણ Xના દસ વિદ્યાર્થીઓ ગણિતના કોયડાની સ્પર્ધામાં ભાગ લે છે. જો ભાગ લેનાર છોકરીઓની સંખ્યા છોકરાઓની સંખ્યા કરતાં 4 વધારે હોય, તો કેટલા છોકરાઓએ અને કેટલી છોકરીઓએ કોયડાની સ્પર્ધામાં ભાગ લીધો હશે તે શોધો.
(ii) 5 પેન્સિલ અને 7 પેનની કુલ કિંમત ₹ 50 છે અને તે જ કિંમતવાળી 7 પેન્સિલ અને 5 પેનની કુલ કિંમત ₹ 46 છે, તો એક પેન્સિલ અને એક પેનની કિંમત શોધો.

ઉત્તરઃ
(i) ધારો કે, x છોકરાઓ અને y છોકરીઓ સ્પર્ધામાં ભાગ લે છે.
આથી આપેલ માહિતી પરથી નીચે મુજબના બે સમીકરણ મળે :
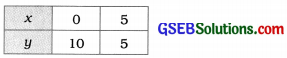
x + y = 10 ……… (1)
અને y = x + 4,
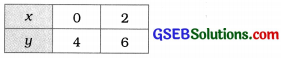
એટલે કે, y – x = 4 …………..(2)
આ સમીકરણોના આલેખ દોરવા આપણે બંને સમીકરણના બે-બે ઉકેલ શોધીને કોષ્ટકમાં દર્શાવીએ. સમીકરણ (1) માટે, x + y = 10 પરથી, y = 10 – x મળે.
સમીકરણ (2) માટે, y – x = 4 પરથી, y = x + 4 મળે.
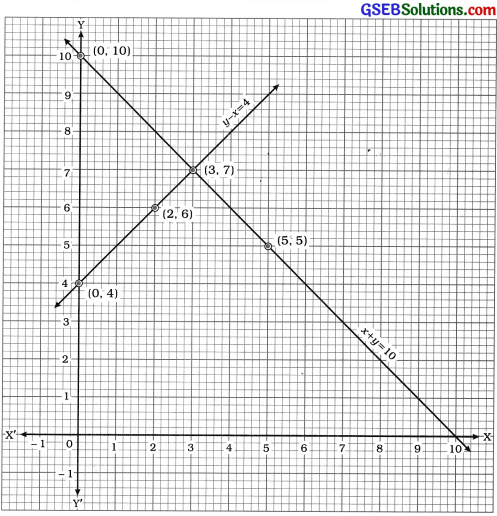
ઉપરોક્ત આલેખમાં બે રેખાઓ બિંદુ (3, 7)માં છેદે છે. આથી x = 3 અને y = 7 એ આપણે મેળવેલ સમીકરણયુગ્મનો ઉકેલ છે. આમ, 3 છોકરાઓ અને 7 છોકરીઓ એ કોયડાની સ્પર્ધામાં ભાગ લીધો હશે. ચકાસણી x = 3 અને U = 7 એ પ્રશ્નમાં આપેલ બંને શરતોનું સમાધાન કરે છે.

(ii) ધારો કે, એક પેન્સિલની કિંમત ₹ x અને એક પેનની કિંમત ₹ y છે.
આથી આપેલ માહિતી પરથી નીચે મુજબના બે સમીકરણ મળે:
5x + 7y = 50 ………. (1)
7x + 5y = 46 ………. (2)
આ સમીકરણોના આલેખ દોરવા આપણે બંને સમીકરણના બે-બે ઉકેલ શોધીને કોષ્ટકમાં દર્શાવીએ.
સમીકરણ (1) માટે, 5x + 7y = 50 પરથી,
y = \(\frac{50-5 x}{7}\) મળે.

સમીકરણ (2) માટે, 7x + 5y = 46 પરથી,
y = \(\frac{46-7 x}{5}\) મળે.
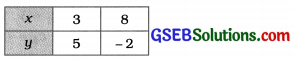
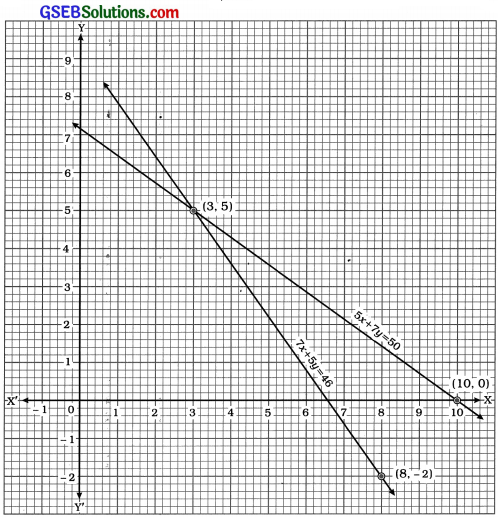
ઉપરોક્ત આલેખમાં બે રેખાઓ બિંદુ (3, 5)માં છેદે છે. આથી x = 3 અને y = 5 એ આપણે મેળવેલ સમીકરણયુગ્મનો ઉકેલ છે. આમ, એક પેન્સિલની કિંમત ₹ 3 અને એક પેનની કિંમત ₹ 5 છે.
ચકાસણીઃ x = 3 અને U = 5 એ બંને સમીકરણ 5x + 7y = 50 અને 7x + 5y = 46નું સમાધાન કરે છે.

પ્રશ્ન 2.
નીચેનાં સુરેખ સમીકરણયુગ્મથી બનતી રેખાઓ એક બિંદુમાં છેદે છે કે સમાંતર છે અથવા સંપાતી છે, તેમ \(\frac{a_{1}}{a_{2}}\), \(\frac{b_{1}}{b_{2}}\) અને \(\frac{c_{1}}{c_{2}}\) ગુણોત્તરોની તુલના કરીને નક્કી કરો:
(i) 5x – 4y + 8 = 0;
72x + 6y – 9 = 0
(ii) 9x + 3y + 12 = 0;
18 + 6y + 24 = 0
(iii) 6x – 3y + 10 = 0;
2x – y + 9 = 0.
ઉત્તરઃ
(1) 5x – 4y + 8 = 0; 7x + 6y – 9 = 0
આપેલ સુરેખ સમીકરણયુગ્મ માટે a1 = 5, b1 = – 4, c1 = 8, a2 = 7, b2 = 6 અને c2 = – 9.
હવે, \(\frac{a_{1}}{a_{2}}=\frac{5}{7}\), \(\frac{b_{1}}{b_{2}}=\frac{-4}{6}=-\frac{2}{3}\)
અને \(\frac{c_{1}}{c_{2}}=\frac{8}{-9}=-\frac{8}{9}\)
અહીં, \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\)
આથી આપેલ સુરેખ સમીકરણયુગ્મથી બનતી રેખાઓ એક બિંદુમાં છેદે છે.

(ii) 9x + 30 + 18 = 0; 18x + 6y + 24 = 0
આપેલ સુરેખ સમીકરણયુગ્મ માટે
a1 = 9, b1 = 3, c1 = 12, a2 = 18, b2 = 6 અને c2 = 24.
હવે, \(\frac{a_{1}}{a_{2}}=\frac{9}{18}=\frac{1}{2}\), \(\frac{b_{1}}{b_{2}}=\frac{3}{6}=\frac{1}{2}\)
અને \(\frac{c_{1}}{c_{2}}=\frac{12}{24}=\frac{1}{2}\)
અહીં, \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
આથી આપેલ સુરેખ સમીકરણયુગ્મથી બનતી રેખાઓ સંપાતી રેખાઓ છે.
(iii) 6x – 3y + 10 = 0; 2x – y + 9 = 0
આપેલ સુરેખ સમીકરણયુગ્મ માટે a1 = 6, b1 = – 3, c1 = 10, a2 = 2, b2 = – 1 અને c2 = 9.
હવે, \(\frac{a_{1}}{a_{2}}=\frac{6}{2}=\), \(\frac{b_{1}}{b_{2}}=\frac{-3}{-1}=3\)
અને \(\frac{c_{1}}{c_{2}}=\frac{10}{9}\)
અહીં, \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
આથી આપેલ સુરેખ સમીકરણયુગ્મથી બનતી રેખાઓ સમાંતર રેખાઓ છે.

પ્રશ્ન 3.
નીચેનાં સુરેખ સમીકરણયુગ્મ સુસંગત છે કે સુસંગત નથી તે ગુણોત્તર \(\frac{a_{1}}{a_{2}}\), \(\frac{b_{1}}{b_{2}}\) અને \(\frac{c_{1}}{c_{2}}\) ની કિંમત પરથી નક્કી કરોઃ
(i) 3x + 2y = 5, 2x – 3y = 7
(ii) 2x – 3y = 8; 4x – 6y = 9
(iii) \(\frac{3}{2}\) x + \(\frac{5}{3}\) y = 7; 9x – 10y = 14
(iv) 5x – 3y = 11; 10x + 6y = – 22
(v) \(\frac{4}{3}\)x + 2y = 8; 2x + 3y = 12
ઉત્તરઃ
(i) 3x + 2y = 5; 2x – 3y = 7
આપેલ સુરેખ સમીકરણયુગ્મ માટે a1 = 3, b1 = 2, c1 = -5, a2 = 2, b2 = -3 અને c2 = – 7.
હવે, \(\frac{a_{1}}{a_{2}}=\frac{3}{2}\), \(\frac{b_{1}}{b_{2}}=\frac{2}{-3}=-\frac{2}{3}\)
અને = \(\frac{c_{1}}{c_{2}}=\frac{-5}{-7}=\frac{5}{7}\)
અહીં, \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\)
આથી આપેલ સુરેખ સમીકરણયુગ્મ સુસંગત છે.

(ii) 2x – 3y = 8; 4x – 6y = 9
આપેલ સુરેખ સમીકરણયુગ્મ માટે a1 = 2, b1 = – 3, c1 = – 8, a2 = 4, b2 = – 6 અને c2 = – 9.
હવે, \(\frac{a_{1}}{a_{2}}=\frac{2}{4}=\frac{1}{2}\), \(\frac{b_{1}}{b_{2}}=\frac{-3}{-6}=\frac{1}{2}\)
અને = \(\frac{c_{1}}{c_{2}}=\frac{-8}{-9}=\frac{8}{9}\)
અહીં, \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
આથી આપેલ સુરેખ સમીકરણયુગ્મ સુસંગત નથી.
(iii) \(\frac{3}{2}\) x + \(\frac{5}{3}\) y = 7; 9x – 10y = 14
પ્રથમ સમીકરણને 6 વડે ગુણ્યા બાદ બંને સમીકરણોને પ્રમાણિત સ્વરૂપમાં દર્શાવતા નીચેનાં સમીકરણો મળે:
9x + 10y – 42 = 0; 9x – 10y – 14 = 0
આપેલ સુરેખ સમીકરણયુગ્મ માટે a1 = 9, b1 = 10, c1 = – 42, a2 = 9, b2 = – 10 અને c2 = – 14.
હવે, \(\frac{a_{1}}{a_{2}}=\frac{9}{9}=1\) , \(\frac{b_{1}}{b_{2}}=\frac{10}{-10}=-1\)
અને \(\frac{c_{1}}{c_{2}}=\frac{-42}{-14}\) = 3.
અહીં, \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\)
આથી આપેલ સુરેખ સમીકરણયુગ્મ સુસંગત છે.

(iv) 5x – 3y = 11; – 10x + 6y = – 22
આપેલ સુરેખ સમીકરણયુગ્મ માટે a1 = 5, b1 = – 3, c1 = – 11, a2 = -10, b2 = 6 અને c2 = 22.
હવે, \(\frac{a_{1}}{a_{2}}=\frac{5}{-10}=-\frac{1}{2}\), \(\frac{b_{1}}{b_{2}}=\frac{-3}{6}=-\frac{1}{2}\)
અને \(\frac{c_{1}}{c_{2}}=\frac{-11}{22}=-\frac{1}{2}\)
અહીં, \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
આથી આપેલ સુરેખ સમીકરણયુગ્મ સુસંગત અને અવલંબી છે.
(v) \(\frac{4}{3}\) x + 20 = 8; 2x + 3y = 12
આપેલ સુરેખ સમીકરણયુગ્મ માટે a1 = 3, b1 = 2, c1 = – 8, a2 = 2, b2 = 3 અને c2 = – 12.
હવે, \(\frac{a_{1}}{a_{2}}=\frac{\frac{4}{3}}{2}=\frac{2}{3}\), \(\frac{b_{1}}{b_{2}}=\frac{2}{3}\)
અને ૬ \(\frac{c_{1}}{c_{2}}=\frac{-8}{-12}=\frac{2}{3}\)
અહીં, \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
આથી આપેલ સુરેખ સમીકરણયુગ્મ સુસંગત અને અવલંબી છે.

પ્રશ્ન 4.
નીચેના પૈકી કયું સુરેખ સમીકરણયુગ્મ સુસંગત છે કે સુસંગત નથી, તે જણાવો. જો સુસંગત હોય, તો ભૌમિતિક રીતે ઉકેલ શોધો.
(i) x + y = 5; 2x + 2y = 10.
(ii) x – y = 8; 3x – 3y = 16
(iii) 2x + y – 6 = 0; 4x – 2y – 4 = 0
(iv) x – 2y – 2 = 0; 4x – 4y – 5 = 0
ઉત્તરઃ
(i) x + y = 5; 2x + 2y = 10.
આપેલ સુરેખ સમીકરણયુગ્મ માટે a1 = 1, b1 = 1, c1 = – 5, a2 = 2, b2 = 2 અને c2 = – 10.
હવે, \(\frac{a_{1}}{a_{2}}=\frac{1}{2}\), \(\frac{b_{1}}{b_{2}}=\frac{1}{2}\)
અને \(\frac{c_{1}}{c_{2}}=\frac{-5}{-10}=\frac{1}{2}\)
અહીં, \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
આથી આપેલ સુરેખ સમીકરણયુગ્મ સુસંગત અને ? અવલંબી છે.
હવે, આપણે બંને સમીકરણના આલેખ દોરીએ.
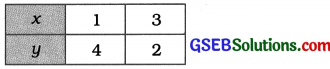
x + y = 5 પરથી, y = 5 – x મળે.
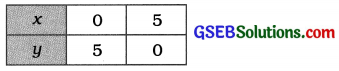
2x + 2y = 10 પરથી, y = \(\frac{10-2 x}{2}\) જ મળે.
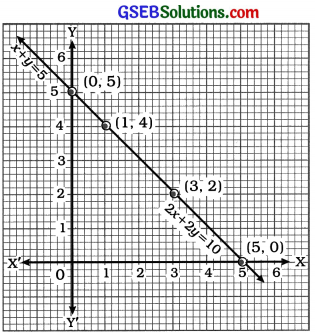
અહીં, બને સમીકરણોની રેખાઓ સંપાતી છે. આથી તે સામાન્ય રેખા પરનું કોઈ પણ બિંદુ સમીકરણયુગ્મનો ઉકેલ આપે. આમ, y = 5 – x, જ્યાં × એ કોઈ વાસ્તવિક સંખ્યા છે, એ આપેલ સમીકરણયુગ્મના ઉકેલ છે.

(ii) x – y = 8; 3x – 3y = 16
આપેલ સુરેખ સમીકરણયુગ્મ માટે a1 = 1, b1 = – 1, c1 = – 8, a2 = 3, b2 = – 3 અને c2 = – 16.
હવે, \(\frac{a_{1}}{a_{2}}=\frac{1}{3}\), \(\frac{b_{1}}{b_{2}}=\frac{-1}{-3}=\frac{1}{3}\)
અને \(\frac{c_{1}}{c_{2}}=\frac{-8}{-16}=\frac{1}{2}\)
અહીં, \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
આથી આપેલ સુરેખ સમીકરણયુગ્મ સુસંગત નથી.
(iii) 2x +y – 6 = 0; 4x – 2y – 4 = 0
આપેલ સુરેખ સમીકરણયુગ્મ માટે a1 = 2, b1 = 1, c1 = – 6, a2 = 4, b2 = -2 અને c2 = -4.
હવે, \(\frac{a_{1}}{a_{2}}=\frac{2}{4}=\frac{1}{2}\), \(\frac{b_{1}}{b_{2}}=\frac{1}{-2}=-\frac{1}{2}\)
અને \(\frac{c_{1}}{c_{2}}=\frac{-6}{-4}=\frac{3}{2}\)
અહીં, \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\)
આથી આપેલ સુરેખ સમીકરણયુગ્મ સુસંગત છે. હવે, આપણે બંને સમીકરણના આલેખ દોરીએ.
2x + y – 6 = 0 પરથી, y = 6 – 2x મળે.
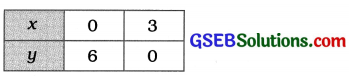
4x – 2y – 4 = 0 પરથી, y = \(\frac{4-2x}{4}\) = 2x – 2 મળે.
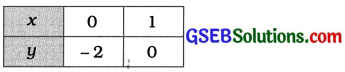
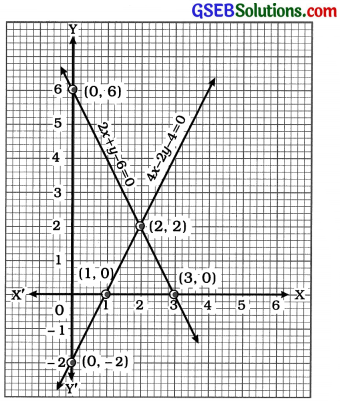
ઉપરોક્ત આલેખમાં બે રેખાઓ બિંદુ (2, 2)માં છેદે છે. આથી x = 2 અને y = 2 એ આપેલ સુરેખ સમીકરણયુગ્મનો ઉકેલ છે.
(iv) 2x – 2y – 2 = 0; 4x – 4y – 5 = 0.
આપેલ સુરેખ સમીકરણયુગ્મ માટે a1 = 2, b1 = -2, c1 = -2, a2 = 4, b2 = -4 અને c2 = – 5.
હવે, \(\frac{a_{1}}{a_{2}}=\frac{2}{4}=\frac{1}{2}\), \(\frac{b_{1}}{b_{2}}=\frac{-2}{-4}=\frac{1}{2}\)
અને \(\frac{c_{1}}{c_{2}}=\frac{-2}{-5}=\frac{2}{5}\).
અહીં, \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
આથી આપેલ સુરેખ સમીકરણયુગ્મ સુસંગત નથી.

પ્રશ્ન 5.
એક લંબચોરસ બગીચાની અર્ધપરિમિતિ 36 મીટર છે તથા તેની લંબાઈ એ તેની પહોળાઈ કરતાં 4 મીટર વધુ છે, તો બગીચાની બાજુઓનાં માપ શોધો.
ઉત્તરઃ
ધારો કે, લંબચોરસ બગીચાની લંબાઈ અને પહોળાઈ અનુક્રમે x મી અને y મી છે,
તો આપેલ માહિતી પરથી નીચે મુજબના સમીકરણ તારવી
શકાય :
લંબાઈ = પહોળાઈ + 4
∴ x = y + 4
અર્ધપરિમિતિ = \(\frac{1}{2}\) × લંબચોરસની પરિમિતિ
∴ 36 = \(\frac{1}{2}\) × 2 (લંબાઈ + પહોળાઈ)
∴ 36 = x + y
∴x + y = 36
હવે આપણે બંને સમીકરણના આલેખ દોરવા બંને સમીકરણના બે-બે ઉકેલ શોધીએ.
x = y + 4 પરથી, y = x – 4 મળે.
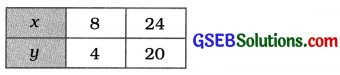
x + y = 36 પરથી, y = 36 – x મળે.
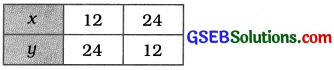
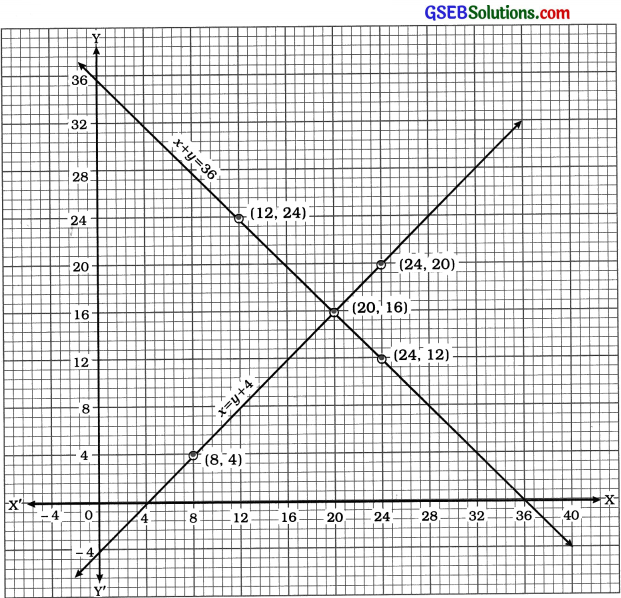
અહીં, બે રેખાઓ બિંદુ (20, 16)માં છેદે છે. આથી x = 20 અને y = 16 એ સમીકરણયુગ્મનો અનન્ય ઉકેલ છે. આમ, બગીચાની લંબાઈ 20 મી અને પહોળાઈ 16 મી છે.

પ્રશ્ન 6.
સુરેખ સમીકરણ 2x + 3g – 8 = 0 આપેલ છે. એવું બીજું દ્વિચલ સુરેખ સમીકરણ લખો કે જેથી તે જોડીનું ભૌમિતિક નિરૂપણ નીચે પ્રમાણે હોય?
(i) છેદતી રેખાઓ
(ii) સમાંતર રેખાઓ
(iii) સંપાતી રેખાઓ
ઉત્તરઃ
(1) છેતી રેખાઓ માટે શરત \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\) નું પાલન થવું જોઈએ.
આપેલ સુરેખ સમીકરણ 2x + 3y – 8 = 0 છે. આપણે જોડીમાંના બીજા સમીકરણ તરીકે 3x + 4y – 24 = 0 લઈ શકીએ. અહીં, \(\frac{a_{1}}{a_{2}}=\frac{2}{3}\) અનેક \(\frac{b_{1}}{b_{2}}=\frac{3}{4}\) હોવાથી \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\) નું પાલન થાય છે.
(ii) સમાંતર રેખાઓ માટે શરત \(\) પાલન થવું જોઈએ. આપેલ સુરેખ સમીકરણ 2x + 3y – 8 = 0 છે. આપણે જોડીમાંના બીજા સમીકરણ તરીકે 6x + 9y – 10 = 0 લઈ શકીએ. અહીં, \([\frac{a_{1}}{a_{2}}=\frac{1}{3}/latex] ,[latex]\frac{b_{1}}{b_{2}}=\frac{1}{3}\) અનેક હોવાથી \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)નું પાલન થાય છે.
(iii) સંપાતી રેખાઓ માટે શરત \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\) નું પાલન થવું જોઈએ. આપેલ સુરેખ સમીકરણ 2x + 3y – 8 = 0 છે. આપણે જાડીમાંના બીજા સમીકરણ તરીકે 10x + 15y – 40 = 0 લઈ શકીએ. અહીં, \(\frac{a_{1}}{a_{2}}=\frac{1}{5}\), \(\frac{b_{1}}{b_{2}}=\frac{1}{5}\) અને \(\frac{c_{1}}{c_{2}}=\frac{1}{5}\) હોવાથી \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\) નું પાલન થાય છે.

પ્રશ્ન 7.
સમીકરણો x – y + 1 = 0 અને 3x + 2y – 12 = 0 દ્વારા દર્શાવાતી રેખાઓના આલેખ દોરો. આ રેખાઓ અને x-અક્ષ દ્વારા રચાયેલા ત્રિકોણનાં શિરોબિંદુઓના યામ દર્શાવો અને બનતા ત્રિકોણાકાર પ્રદેશને છાયાંકિત કરો.
ઉત્તરઃ
x – y + 1 = 0 પરથી, y = x + 1 મળે.
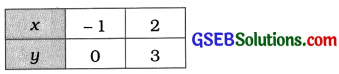
3x + 2y – 12 = 0 પરથી, y = \(\frac{12-3x}{2}\) મળે.
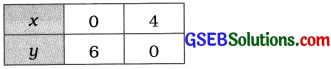
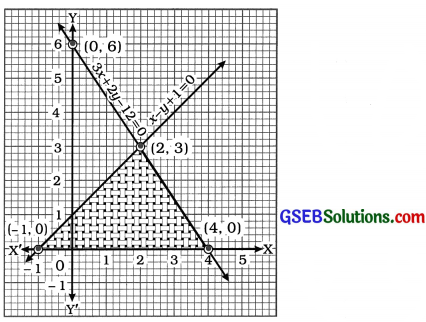
આલેખમાં રેખાઓ અને x-અક્ષ દ્વારા રચાયેલા ત્રિકોણનાં શિરોબિંદુઓના (-1, 0), (4, 0) તથા (2, 3) છે.