GSEB Solutions Class 10 Maths Chapter 3 દ્વિચલ સુરેખ સમીકરણયુગ્મ Ex 3.5

Gujarat Board GSEB Solutions Class 10 Maths Chapter 3 દ્વિચલ સુરેખ સમીકરણયુગ્મ Ex 3.5 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 10 Maths Chapter 3 દ્વિચલ સુરેખ સમીકરણયુગ્મ Ex 3.5

પ્રશ્ન 1.
નીચેના પૈકી કયા સુરેખ સમીકરણયુગ્મને અનન્ય ઉકેલ નથી અથવા અનંત ઉકેલો છે, તે જણાવો. જો અનન્ય ઉકેલ હોય, તો ચોકડી ગુણાકારની રીતે તેનો ઉકેલ શોધો.
(i) x – 3y – 3 = 0
3x – 9y – 2 = 0

(ii) 2x + y = 5.
3x + 2y = 8

(iii) 3x – 5y = 20
6x – 10y = 40

(iv) x – 3y – 7 = 0
3x – 3y – 15 = 0

ઉત્તરઃ
(i) x – 3y – 3 = 0 અને 3x – 9y – 2 = 0
અહ, a₁ = 1; a₂ = 3; b₁ = – 3; b₂ = -9; c₁ = – 3 અને c₂ = – 2.
હવે, \(\frac{a_{1}}{a_{2}}=\frac{1}{3}\), \(\frac{b_{1}}{b_{2}}=\frac{-3}{-9}=\frac{1}{3}\) અને \(\frac{c_{1}}{c_{2}}=\frac{-3}{-2}=\frac{3}{2}\)

અહીં, \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
આથી આપેલ સુરેખ સમીકરણયુગ્મને અનન્ય ઉકેલ નથી.

(ii) 2x + y – 5 = 0 અને 3x + 2y – 8 = 0
અહીં, a₁ = 2; a₂ = 3; b₁ = 1; b₂ = 2; c₁ =-5 અને c₂ = – 8.
હવે, \(\frac{a_{1}}{a_{2}}=\frac{2}{3}\), \(\frac{b_{1}}{b_{2}}=\frac{1}{2}\) અને \(\frac{c_{1}}{c_{2}}=\frac{-5}{-8}=\frac{5}{8}\)

અહીં, \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\)
આથી આપેલ સુરેખ સમીકરણયુગ્મને અનન્ય ઉકેલ છે.
હવે,

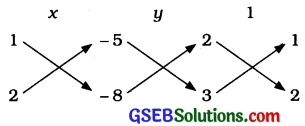
\(\frac{x}{(1)(-8)-(2)(-5)}=\frac{y}{(-5)(3)-(-8)(2)}\) = \(\frac{1}{(2)(2)-(3)(1)}\)

\(\frac{x}{-8+10}=\frac{y}{-15+16}=\frac{1}{4-3}\) \(\frac{x}{2}=\frac{y}{1}=\frac{1}{1}\)

\(\frac{x}{2}=\frac{1}{1}\) અને \(\frac{y}{1}=\frac{1}{1}\)

∴ x = 2 અને y = 1
આમ, આપેલ સુરેખ સમીકરણયુગ્મનો અનન્ય ઉકેલ x = 2, y = 1 છે.

(iii) 3x – 5y – 20 = 0 અને 6x – 10y – 40 = 0
અહીં, a₁ = 3; a₂ = 6, b₁ = – 5; b₂ = – 10; c₁ = – 20 અને c₂ = – 40.
હવે, \(\frac{a_{1}}{a_{2}}=\frac{3}{6}=\frac{1}{2}\), \(\frac{b_{1}}{b_{2}}=\frac{-5}{-10}=\frac{1}{2}\) અને \(\frac{c_{1}}{c_{2}}=\frac{-20}{-40}=\frac{1}{2}\)

અહીં, \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
આમ, આપેલ સુરેખ સમીકરણયુગ્મને અનંત ઉકેલ છે.

(iv) x – 3y – 7 = 0 અને 3x – 3y – 15 = 0
અહીં, a₁ = 1; a₂ = 3; b₁ =-3; b₂ =-3; c₁ =-7 અને c₂ = – 15.
હવે, \(\frac{a_{1}}{a_{2}}=\frac{1}{3}\), \(\frac{b_{1}}{b_{2}}=\frac{-3}{-3}\) = 1 અને \(\frac{c_{1}}{c_{2}}=\frac{-7}{-15}=\frac{7}{15}\)

અહીં, \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\)

આથી આપેલ સુરેખ સમીકરણયુગ્મને અનન્ય ઉકેલ છે.
હવે,

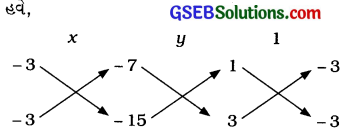
\(\frac{x}{(-3)(-15)-(-3)(-7)}=\frac{y}{(-7)(3)-(-15)(1)}\) = \(\frac{1}{(1)(-3)-(3)(-3)}\)

\(\frac{x}{45-21}=\frac{y}{-21+15}=\frac{1}{-3+9}\) \(\frac{x}{24}=\frac{y}{-6}=\frac{1}{6}\)

\(\frac{x}{24}=\frac{1}{6}\) અને \(\frac{y}{-6}=\frac{1}{6}\)

∴ x = 4 અને y = – 1
આમ, આપેલ સુરેખ સમીકરણયુગ્મનો અનન્ય ઉકેલ x = 4, y = -1 છે.

પ્રશ્ન 2.
(i) નીચેના સુરેખ સમીકરણયુગ્મને a અને b ની કઈ કિંમતો માટે અનંત ઉકેલો છે?
2x + 3y = 7
(a – b) x + (a + b) y = 3a + b – 2,

(ii) નીચેના સુરેખ સમીકરણયુગ્મને k ની કઈ કિંમત માટે ઉકેલ ન મળે?
3x + y = 1
(2k – 1) x + (k – 1) y = 3k + 1 (1)
ઉત્તરઃ
આપેલ સમીકરણોને પ્રમાણિત સ્વરૂપમાં દર્શાવતાં,
2x + 3y – 7 = 0 અને (a – b) x + (a + b) y – (3a + b – 2) = 0 મળે.
અહીં, A₁ = 2; A₂ = a – b; B₁ = 3; B₂ = a + b; C₁ = – 7 અને C₂ = (3a + b – 2)
આથી \(\frac{A_{1}}{A_{2}}=\frac{2}{a-b}\), \(\frac{\mathrm{B}_{1}}{\mathrm{~B}_{2}}=\frac{3}{a+b}\) અને \(\frac{C_{1}}{C_{2}}=\frac{-7}{-(3 a+b-2)}=\frac{7}{3 a+b-2}\)
આપેલ સુરેખ સમીકરણયુગ્મને અનંત ઉકેલો હોય, તો \(\frac{\mathrm{A}_{1}}{\mathrm{~A}_{2}}=\frac{\mathrm{B}_{1}}{\mathrm{~B}_{2}}=\frac{\mathrm{C}_{1}}{\mathrm{C}_{2}}\) થાય.

\(\frac{2}{a-b}=\frac{3}{a+b}=\frac{7}{3 a+b-2}\)

હવે, \(\frac{2}{a-b}=\frac{3}{a+b}\)
2 (a + b) = 3 (a – b)
2a + 2b = 3a – 3b
5b = a
∴ a = 5b ……………… (1)
વળી, \(\frac{3}{a+b}=\frac{7}{3 a+b-2}\)

∴ 3 (3a + b – 2) = 7 (a + b)
∴ 9a + 3b – 6 = 7a + 7b
2a – 4b = 6
2 (5b) – 4b = 6 [(1) મુજબ, a = 5b]
6b = 6.
b = 1
હવે, a = 5b
∴ a = 5 (1)
∴ a = 5.
આમ, a = 5 અને b = 1 માટે આપેલ સુરેખ સમીકરણયુગ્મને અનંત ઉકેલો છે.

(ii) આપેલ સમીકરણોને પ્રમાણિત સ્વરૂપમાં દર્શાવતાં,
3x + y – 1 = 0 અને (2k – 1) x + (k – 1) y – (2k + 1) = 0 મળે.
અહીં, a₁ = 3; a₂ = 2k – 1; b₁ = 1; b₂ = k- 1; c₁ = – 1 અને c₂ = – (2k + 1)
આસી. \(\frac{a_{1}}{a_{2}}=\frac{3}{2 k-1}\), \(\frac{b_{1}}{b_{2}}=\frac{1}{k-1}\) અને \(\frac{c_{1}}{c_{2}}=\frac{-1}{-(2 k+1)}=\frac{1}{2 k+1}\)

જો આપેલ સુરેખ સમીકરણયુગ્મને ઉકેલ ન મળે, તો નીચેની શરતનું પાલન થાયઃ
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)

\(\frac{3}{2 k-1}=\frac{1}{k-1} \neq \frac{1}{2 k+1}\) \(\frac{3}{2 k-1}=\frac{1}{k-1}\)

3(k – 1) = 2k – 1
3 k – 3 = 2k – 1
k = 2
k = 2 માટે,
\(\frac{a_{1}}{a_{2}}=\frac{3}{2(2)-1}\) = 1, \(\frac{b_{1}}{b_{2}}=\frac{1}{2-1}\) = 1 અને \(\frac{c_{1}}{c_{2}}=\frac{1}{2(2)+1}=\frac{1}{5}\)

આથી k = 2 દ્વારા \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\) નું પાલન થાય છે.
આમ, k = 2 માટે આપેલ સુરેખ સમીકરણયુગ્મનો ઉકેલ ન મળે.

પ્રશ્ન 3.
નીચેના સુરેખ સમીકરણયુગ્મનો ઉકેલ આદેશની રીતે અને ચોકડી ગુણાકારની રીતે શોધોઃ
8x + 5y = 9
3x + 2y = 4
ઉત્તરઃ
(i) આદેશની રીતઃ
8x + 5y = 9 ……………(1)
3x + 2y = 4 ……………. (2)
સમીકરણ (2)માંથી y = \(\frac{4-3 x}{2}\) મળે.
સમીકરણ (1)માં y = \(\frac{4-3 x}{2}\) મૂકતાં,
8x + 5 (\(\frac{4-3 x}{2}\)) = 9
16x + 5 (4 – 3x) = 18 (2 વડે ગુણતાં) .
16x + 20 – 15x = 18
∴ x = – 2
y = \(\frac{4-3 x}{2}\) માં x = – 2 મૂકતાં,

y = \(\frac{4-3(-2)}{2}\)
∴ y = \(\frac{10}{2}\)
∴ y = 5
આમ, આપેલ સુરેખ સમીકરણયુગ્મનો ઉકેલ x = – 2, y = 5 છે.

(ii) ચોકડી ગુણાકારની રીતઃ
આપેલ સમીકરણોને પ્રમાણિત સ્વરૂપમાં દર્શાવતાં,
8x + 5y – 9 = 0 અને 3x + 2y – 4 = 0 મળે. અહીં, a₁ = 8; b₁ = 5; c₁ = – 9; a₂ = 3; b₂ = 2 અને c₂ = – 4 આથી

આથી

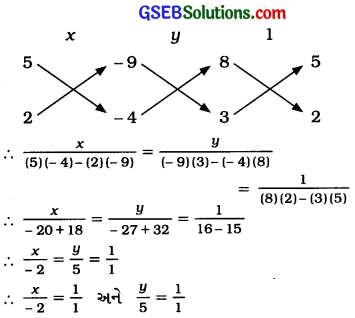
∴ x = – 2 અને y = 5 આમ, આપેલ સુરેખ સમીકરણયુગ્મનો ઉકેલ x = – 2, y = 5 છે.

પ્રશ્ન 4.
નીચેના કૂટપ્રશ્નોમાં સુરેખ સમીકરણયુગ્મ મેળવો અને કોઈ પણ બૈજિક રીતે તેમના ઉકેલ (જો શક્ય હોય તો) શોધોઃ

(i) એક હોસ્ટેલના વિદ્યાર્થીઓનું ભોજન-ખર્ચ અંશતઃ અચળ અને અંશતઃ વિદ્યાર્થીઓએ જેટલા દિવસ ભોજન લીધું હોય તે દિવસોની સંખ્યાના પ્રમાણમાં હોય છે. વિદ્યાર્થી 4, 20 દિવસ ભોજન લે છે અને તેનું ભોજન-ખર્ચ ર 1000 ચૂકવે છે. વિદ્યાર્થી 8, 26 દિવસ ભોજન લે છે અને ભોજન-ખર્ચ પેટે ર1180 ચૂકવે છે, તો નિશ્ચિત ખર્ચ તથા દૈનિક ભોજન-ખર્ચ શોધો.
ઉત્તરઃ
ધારો કે, નિશ્ચિત માસિક દર x અને દૈનિક ભોજનખર્ચ ૨g છે.
તો, આપેલ માહિતી પરથી નીચે મુજબના બે સુરેખ સમીકરણો મળે :
x + 20y = 1000 …………(1)
x + 26y = 1180 …….. (2)
સમીકરણોને પ્રમાણિત સ્વરૂપમાં દર્શાવતાં,
x + 20y – 1000 = 0 …………. (3)
x + 26u-1180 = 0 ……………. (4)
હવે, આપણે સમીકરણયુગ્મનો ઉકેલ ચોકડી ગુણાકારની રીતે શોધીએ.
અહીં, a₁ = 1; a₂ = 1; b₁ = 20; b₂ = 26; c₁ = – 1000 અને c₂ = – 1180

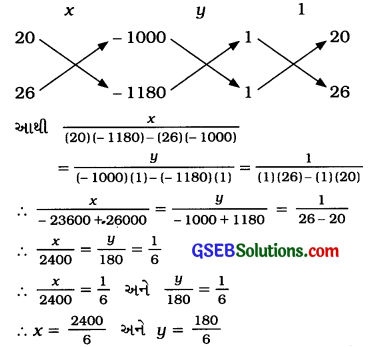
∴ x = 400 અને y = 30
આમ, નિશ્ચિત માસિક દર ₹ 400 અને દૈનિક ભોજનખર્ચ ₹ 30 છે.
નોંધઃ અહીં, લોપની રીત ખૂબ જ સહેલી પડે તેમ છે, પરંતુ ચોકડી ગુણાકારની રીતનો વધુ ઉપયોગ શિખાય તે – માટે ચોકડી ગુણાકારની રીત બતાવી છે.

(ii) એક અપૂર્ણાકના અંશમાંથી 1 બાદ કરવામાં આવે તો નવા અપૂર્ણાકનું અતિસંક્ષિપ્ત સ્વરૂપ \(\frac{1}{3}\) છે અને તે જ અપૂર્ણાકના છેદમાં 8 ઉમેરવામાં આવે, તો મળતા અપૂર્ણાકનું અતિસંક્ષિપ્ત સ્વરૂપ \(\frac{1}{4}\) થાય છે, તો તે અપૂર્ણાક શોધો.
ઉત્તરઃ
ધારો કે, માગેલ અપૂર્ણાકનો અંશ x અને છેદ પુ. છે. માટે, માગેલ અપૂર્ણાંક = \(\frac{x}{y}\)
તો, આપેલ માહિતી મુજબ
\(\frac{x-1}{y}=\frac{1}{3}\)
∴ 3x – 3 = 9
∴ 3x – y = 3 ………….. (1)
અને \(\frac{x}{y+8}=\frac{1}{4}\)
∴ 4x = y + 8
∴ 4x – y = 8 …………. (2)
સમીકરણ (2)માંથી સમીકરણ (1) બાદ કરતાં,
(4x – y) – (3x – y) = 8 – 3
4x – y – 3x + y = 5
x = 5.
સમીકરણ (1)માં x = 5 મૂક્તાં,
3 (5) – y = 3
∴ 15 – 3 = y
∴ y = 12,
આમ, માગેલ અપૂર્ણાંક = \(\frac{x}{y}=\frac{5}{12}\).

(iii) યશને એક કસોટીમાં 40 ગુણ મળ્યા હતા. તેને પ્રત્યેક સાચા જવાબના 3 ગુણ મળે છે અને પ્રત્યેક ખોટા જવાબ માટે 1 ગુણ કપાય છે. જો પરીક્ષકે દરેક સત્ય જવાબ માટે 4 ગુણ આપ્યા હોત અને દરેક ખોટા જવાબ માટે 2 ગુણ કાપ્યા હોત, તો થશે 50 ગુણ મેળવ્યા હોત. તો આ કસોટીમાં કેટલા પ્રશ્નો હતા?
ઉત્તરઃ
ધારો કે, યશ આપેલ જવાબોમાં x જવાબ સાચા અને પુ જવાબ ખોટા છે. તો, આપેલ માહિતી પરથી નીચેના સમીકરણો મળે:
3x – y = 40 ………….(1)
4x – 2y = 50, એટલે કે, 2x – y = 25 …… (2)
આ સમીકરણોને પ્રમાણિત સ્વરૂપમાં દર્શાવતાં,
3x – y – 40 = 0 …………(3)
2x – y – 25 = 0 ………….(4)

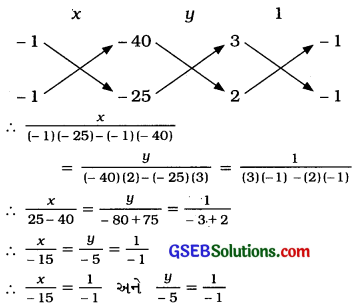
∴ x = 15 અને y = 5.
આથી કસોટીમાં પુછાયેલ કુલ પ્રશ્નો = x + y = 15 + 5 = 20
આમ, કસોટીમાં કુલ 20 પ્રશ્નો હતા.

(iv) ધોરીમાર્ગ પર સ્થાન A અને સ્થાન B એકબીજાથી 100 કિમી દૂર છે. એક ગાડી Aથી ઊપડે છે અને બીજી ગાડી Bથી ઊપડે છે. ગાડીઓ એક જ દિશામાં ભિન્ન પરંતુ એકધારી ઝડપથી ચાલે તો 5 કલાકમાં એકબીજાને મળે છે. તેઓ એકબીજા તરફ ચાલે તો તે 1 કલાકમાં મળે છે, તો બે ગાડીઓની ઝડપ કેટલી હશે?
ઉત્તરઃ
ધારો કે, સ્થાન નથી ઊપડતી ગાડીની ઝડપ ૪ કિમી / કલાક અને સ્થાન Bથી ઊપડતી ગાડીની ઝડપ પુ કિમી / કલાક છે, જ્યાં x> ૫. જો ગાડીઓ એક જ દિશામાં ચાલતી હોય તો તે બંને Aથી B તરફની દિશામાં ગતિ કરતી હોય, કારણ કે તેથી ઊપડતી ગાડીની ઝડપ Bથી ઊપડતી ગાડીની ઝડપ કરતાં વધુ છે.

ધારો કે, ગાડીઓ એક જ દિશામાં ચાલીને 5 કલાક બાદ P સ્થાન પર મળે છે.
5 કલાકમાં A સ્થાનથી ઊપડતી ગાડીએ કાપેલ અંતર AP = 5x કિમી. (અંતર = ઝડપ ૪ સમય).
તે જ રીતે, 5 કલાકમાં સ્થાન Bથી ઊપડતી ગાડીએ કાપેલ અંતર BP = 5y કિમી.
હવે, AB = 100 કિમી .
∴ AP – BP = 100
∴ 5x – 5y = 100
∴ x – y = 20 (5 વડે ભાગતાં)

હવે, ધારો કે ગાડીઓ વિરુદ્ધ દિશામાં ચાલીને 1 કલાક બાદ 9 સ્થાન પર મળે છે.
1 કલાકમાં A સ્થાનથી ઊપડતી ગાડીએ કાપેલ અંતર AQ = x કિમી.
તે જ રીતે, 1 કલાકમાં B સ્થાનથી ઊપડતી ગાડીએ કાપેલ અંતર BQ = y કિમી.
હવે, AB = 100 કિમી
∴ AQ + BQ = 100
∴ x + y = 100 ……. (2)
સમીકરણો (1) અને (2)નો સરવાળો લેતાં,
(x – y) + (x + y) = 20 + 100
∴ 2x = 120
∴ x = 60
સમીકરણ (2)માં x = 60 મૂકતાં,
60 + y = 100
∴ y = 40
આમ, સ્થાન A પરથી ઊપડતી ગાડીની ઝડપ સ્થાન B પરથી ઊપડતી ગાડીની ઝડપ કરતાં વધુ છે તે ધારણા મુજબ સ્થાન મથી ઊપડતી ગાડીની ઝડપ 60 કિમી / કલાક અને
સ્થાન Bથી ઊપડતી ગાડીની ઝડપ 40 કિમી / કલાક છે.

(v) જો એક લંબચોરસની લંબાઈમાં 5 એકમ ઘટાડો થાય અને પહોળાઈમાં ૩ એકમ વધારો થાય, તો લંબચોરસનું ક્ષેત્રફળ 9 ચોરસ એકમ જેટલું ઘટે છે. જો આપણે લંબાઈમાં 3 એકમ અને પહોળાઈમાં 2 એકમ વધારીએ, તો ક્ષેત્રફળ 67 ચોરસ એકમ વધે છે, તો લંબચોરસનાં પરિમાણ શોધો.
ઉત્તરઃ
ધારો કે, લંબચોરસની લંબાઈ × એકમ અને પહોળાઈ u એકમ છે.
લંબચોરસનું ક્ષેત્રફળ = લંબાઈ × પહોળાઈ
∴ આપેલ લંબચોરસનું ક્ષેત્રફળ = xy ચોરસ એકમ પ્રથમ શરત મુજબ, ઘટાડેલ લંબાઈ = (x – 5) એકમ,
વધારેલ પહોળાઈ = (y + 3) એકમ થાય અને ક્ષેત્રફળ = (xy – 9) ચોરસ એકમ થાય.
હવે, લંબાઈ × પહોળાઈ = લંબચોરસનું ક્ષેત્રફળ .
∴ (x – 5) (y + 3) = xy – 9
∴ xy + 3x – 5y – 15 = xy – 9
∴ 3x – 5y – 6 = 0 ………. (1)
તે જ રીતે, દ્વિતીય શરત મુજબ, વધારેલ લંબાઈ = (x + 3)
એકમ, વધારેલ પહોળાઈ = (y + 2)
એકમ અને ક્ષેત્રફળ = (xy + 67) ચોરસ એકમ થાય.
હવે, લંબાઈ × પહોળાઈ = લંબચોરસનું ક્ષેત્રફળ
∴ (x + 3) (y + 2) = xy + 67
∴ xy + 2x + 3y + 6 = xy + 67
∴ 2x + 3y – 61 = 0 …………… (2)
સમીકરણયુગ્મનો ઉકેલ આપણે ચોકડી ગુણાકારની રીતે મેળવીએ.

∴ x = 17 અને y = 9
આમ, આપેલ લંબચોરસની લંબાઈ અને પહોળાઈ અનુક્રમે 17 એકમ અને ૭ એકમ છે.