GSEB Solutions Class 10 Maths Chapter 5 સમાંતર શ્રેણી Ex 5.3

Gujarat Board GSEB Solutions Class 10 Maths Chapter 5 સમાંતર શ્રેણી Ex 5.3 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 10 Maths Chapter 5 સમાંતર શ્રેણી Ex 5.3

પ્રશ્ન 1.
નીચે આપેલ સમાંતર શ્રેણી માટે માગ્યા પ્રમાણે સરવાળો શોધોઃ
(i) 2, 7, 12, …….., 10 પદ સુધી
(ii) – 37, 33, – 29, ………., 12 પદ સુધી
(iii) 0.6, 1.7, 2.8, ………….., 100 પદ સુધી
(iv) \(\frac{1}{15}\), \(\frac{1}{12}\), \(\frac{1}{10}\), …………., 11 પદ સુધી

ઉત્તરઃ
(i) આપેલ સમાંતર શ્રેણી 2, 7, 12, ……. માટે a = 2, d = 7 – 2 = 5, n = 10 અને S_n શોધવાનો છે.
S_n = \(\frac{n}{2}\) [2a + (n – 1)d]
S_n = \(\frac{10}{2}\) [4 + (10 – 1) 5] = 5 (49) = 245
આમ, આપેલ સમાંતર શ્રેણીનાં પ્રથમ 10 પદોનો સરવાળો 245 થાય.

(ii) આપેલ સમાંતર શ્રેણી – 37, – 33, – 29, …….. માટે
a = – 37, d = (- 33) – (- 37) = 4, n = 12 અને S_n શોધવાનો છે.
S_n = \(\frac{n}{2}\) [2a + (n – 1) d]
S₁₂ = \(\frac{12}{2}\) [- 74 + (12 – 1) 4]
= 6(- 30) = – 180
આમ, આપેલ સમાંતર શ્રેણીનાં પ્રથમ 12 પદોનો સરવાળો – 180 થાય.

(iii) આપેલ સમાંતર શ્રેણી 0.6, 1.7, 2.8, … માટે
a = 0.6, d = 1.7 – 0.6 = 1.1, n = 100 અને S_n શોધવાનો છે.
S_n = \(\frac{n}{2}\) [2a + (n-1) d]
∴ S₁₀₀ = \(\frac{n}{2}\) [1.2 + (100 – 1) (1.1)]
= 50 [1.2 + 108.9].
= 50 × 110.1 = 5505
આમ, આપેલ સમાંતર શ્રેણીનાં પ્રથમ 100 પદોનો સરવાળો 5505 થાય.

(iv) આપેલ સમાંતર શ્રેણી \(\frac{1}{15}\), \(\frac{1}{12}\), \(\frac{1}{105}\), ……….. માટે,
a = \(\frac{1}{15}\) d = \(\frac{1}{12}\) – \(\frac{1}{15}\) = \(\frac{5-4}{60}\)

= \(\frac{1}{60}\) અને S_n શોધવાનો છે.
S_n = \(\frac{n}{2}\) [2a + (n – 1) d] .
∴ S₁₁ = \(\frac{11}{2}\) [\(\frac{2}{15}\) + (11 – 1) (\(\frac{1}{60}\))]

= \(\frac{11}{2}\left[\frac{2}{15}+\frac{1}{6}\right]\)

= \(\frac{11}{2}\left[\frac{4+5}{30}\right]=\frac{11}{2} \times \frac{9}{30}=\frac{33}{20}\)
આમ, આપેલ સમાંતર શ્રેણીનાં પ્રથમ 11 પદોનો સરવાળો \(\frac{33}{20}\) થાય.

પ્રશ્ન 2.
નીચેના સરવાળા શોધો (સમાંતર શ્રેણી આપેલ છે.)
(i) 7 + 10\(\frac{1}{2}\) + 14 + …………. + 84
(ii) 34 + 32 +30+…………. + 10
(iii) (- 5) + (- 8) + (- 11) + …………. + (- 230)
ઉત્તરઃ
(i) 7 + 10\(\frac{1}{2}\) + 14 + ………. + 84
અહીં, a = 7; d = 10\(\frac{1}{2}\) – 7 = 3\(\frac{1}{2}\) ; અંતિમ પદ l = 84.
ધારો કે, અંતિમ પદ એ તમું પદ છે.
a_n = a + (n – 1) d
84 = 7 + (n – 1) (33)
77 = \(\frac{7}{2}\) (n – 1)
(n – 1) = 22
n = 23
હવે,
S_n = \(\frac{n}{2}\) (a + l); જ્યાં, ! એ અંતિમ પદ છે.
= \(\frac{23}{2}\) (7 + 84)
= \(\frac{23}{2}\) × 91 = 1046\(\frac{1}{2}\)
આમ, માગેલ સરવાળો 1046\(\frac{1}{2}\) થાય.

(ii) 34 + 32 + 30 + …………. + 10
અહીં, a = 34; d = 32 – 34 = (- 2);
અંતિમ પદ l = 10.
ધારો કે, અંતિમ પદ એ તમું પદ છે.
a_n = a + (n – 1) d
10 = 34 + (n – 1) (- 2)
– 24 = – 2 (n – 1)
(n – 1) = 12
∴ n = 13
S_n = \(\frac{n}{2}\) (a + l); જ્યાં, l એ અંતિમ પદ છે.
= \(\frac{13}{2}\) (34 + 10)
= 13 × 22 = 286
આમ, માગેલ સરવાળો 286 થાય.

(iii) (- 5) + (-8) + (- 11) + …………. + (- 230)
અહીં, a = (- 5); d = (- 2) – (- 5) = (- 3);
અંતિમ પદ l = (- 230).
ધારો કે, અંતિમ પદ એ મું પદ છે.
a_n = a + (n – 1) d
– 230 = – 5 + (n – 1) (- 3)
– 225 = – 3 (n – 1)
∴ n – 1 = 75 :
∴ n = 76
હવે, S_n = \(\frac{n}{2}\) (a + l); જ્યાં, 1 એ અંતિમ પદ છે.
= \(\frac{n}{2}\) [(- 5) + (- 230)]
= 38 (- 235) = – 8930
આમ, માગેલ સરવાળો – 8930 થાય.

પ્રશ્ન 3.
સમાંતર શ્રેણીમાં
(i) a = 5, d = 3, a_n, = 50 આપેલ હોય, તો n અને S_n શોધો.
(ii) a = 7, a₁₃ = 35 આપેલ હોય, તો d અને S₁₃ શોધો.
(iii) a₁₂ = 37, d = 3 આપેલ હોય, તો વ અને S₁₂ શોધો.
(iv) d = 15, S₁₀ = 125 આપેલ હોય, તો અને a₉ શોધો.
(v) d = 5, S₉ = 75 આપેલ હોય, તો a અને a₉ શોધો.
(vi) a = 2, d = 8, S_n = 90 આપેલ હોય, તો n અને a_n શોધો.
(vii) a = 8, a_n = 62, S_n = 210 આપેલ હોય, તો n અને a શોધો.
(viii) a_n = 4, d = 2, S_n = – 14 આપેલ હોય, તો n અને a શોધો.
(ix) a = 3, n = 8, S = 192 આપેલ હોય, તો d શોધો.
(x) l = 28, S = 144 હોય અને પદોની સંખ્યા 9 હોય તો a શોધો.

ઉત્તરઃ
(i) d = 5, d = 3, a_n = 50, n = ? S_n = ?
a_n = a + (n – 1)d
50 = 5 + (n – 1) 3
45 = 3(n – 1)
15 = n – 1
n = 16
S_n = \(\frac{n}{2}\) (a + l)
S₁₆ = \(\frac{16}{2}\) (5 + 50)
S₁₆ = 8 × 55
S₁₆ = 440.

(ii) a = 7, a₁₃ = 35, d =?, S₁₃ = ?
a_n = a + (n – 1) d
a₁₃ = a + (13 – 1) d
35 = 7 + 12d
28 = 12 d
d = \(\frac{28}{12}\)
d = \(\frac{7}{3}\)
S_n = \(\frac{n}{2}\) (a + l)
S₁₃ = \(\frac{13}{2}\) (7 + 35)
S₁₃ = 13 × 21
S₁₃ = 278

(iii) a₁₂ = 37, d= 3 a = ?, S₁₂ = ?
a_n = a + (n – 1)d
a₁₂ = a + 11d
37 = a + 11 (3)
∴ a = 4
S_n = \(\frac{n}{2}\) (a + l)
S₁₂ = \(\frac{12}{2}\) (4 + 37)
∴ S₁₂ = 246

(iv) a₃ = 15, S₁₀ = 125, d = ?, a₁₀ = ?
a_n = a + (n – 1)d
a₃ = a + 2d
a + 2d = 15 ………… (1)
S_n = \(\frac{n}{2}\) [2a + (n – 1)d)
S₁₀ = \(\frac{10}{2}\) [12a + 9d]
125 = 5 (2a + 9d)
2a + 9d = 25 …………….(2)
સમીકરણ (1) અને (2) પરથી d = – 1 અને a = 17.
a_n = a + (n – 1)d
a₁₀ = a + 9d
a₁₀ = 17 + 9(- 1)
a₁₀ = 8

(v) d = 5, S₉ = 75, a = ?, a₉ = ?
S_n = \(\frac{n}{2}\) [2a + (n – 1)d)
S₉ = \(\frac{9}{2}\) [2a + (9 – 1)d]
75 = \(\frac{9}{2}\) [2a + 8 (5)]
75 = 9 (a + 20)
\(\frac{25}{3}\) = a + 20
a = \(\frac{25}{3}\)– 20
a = \(-\frac{35}{3}\)
a_n = a + (n – 1)d
a₉ = a + 8d
a₉ = (\(-\frac{35}{3}\)) + 8 (5)
a₉ = \(-\frac{35}{3}\) + 40
a₉ = \(\frac{85}{3}\)

(vi) a = 2, d = 8, S_n = 90, n = ?, a_n = ?
S_n = \(\frac{n}{2}\) [12a + (n – 1)d]
90 = \(\frac{n}{2}\) [4 + (n – 1)8]
90 = \(\frac{n}{2}\) (8n – 4)
90 = n (4n – 2]
4n² – 2n – 90 = 0
2n² – n – 45 = 0
2n² – 10n + 9n – 45 = 0
2n (n – 5) + 9 (n – 5) = 0
(n – 5) (2n + 9) = 0
∴ n – 5 = 0 અથવા 2n + 9 = 0
∴ n = 5 અથવા n = – \(\frac{9}{2}\)
∴ n = 5
a_n= a + (n – 1)d
a₅ = a + 4d
a₅ = 2 + 4(8)
a₅ = 34

(vii) a = 8, a_n = 62, S_n = 210, n = ? d = ?
S_n = \(\frac{n}{2}\) (a + l)
S_n = \(\frac{n}{2}\) (a + a_n)
210 = \(\frac{n}{2}\) (8 + 62)
420 = n (70)
n = 6
a_n = a + (n – 1)d
a₆ = a + 5d
62 = 8 + 5d
54 = 5d
d = \(\frac{54}{5}\)

(viii) a_n = 4, d = 2, S_n = – 14, n = ?, a = ?.
a_n = a + (n – 1)d
4 = a + (n – 1) (2)
4 = a + 2n – 2
a = 6 – 2n ………. (1)
S_n = \(\frac{n}{2}\) [2a + (n – 1)d]
– 14 = \(\frac{n}{2}\) [2(6 – 2n) + (n – 1) (2)] ((1) મુજબ)
– 14 = \(\frac{n}{2}\) [12 – 4n + 2n – 2].
– 14 = \(\frac{n}{2}\) [- 2n + 10].
– 14 = n (- n + 5).
– 14 = – n² + 5n
n² – 5n – 14 = 0
(n – 7) (n + 2) = 0
n – 7 = 0 અથવા n + 2 = 0
n = 7 અથવા n = – 2
n ધન પૂર્ણાક હોવાથી n ≠ – 2.
∴ n = 7
(1) મુજબ, a = 6 – 2n
∴ a = 6 – 2 (7).
∴ a = – 8

(ix) a = 3, n = 8, S_n = 192, d = ?
S_n = \(\frac{n}{2}\) [2a + (n – 1) d]
192 = \(\frac{8}{2}\) [16 + (8 – 1) d]
192 = 4 [6 + 7d]]
48 = 6 + 7d
42 = 7d
d = 6.

(x) l = 28, S = 144, n = 9, a =?
S_n = \(\frac{n}{2}\) (a + l)
144 = \(\frac{9}{2}\) (a + 28)
32 = (a + 28)
a = 4.

પ્રશ્ન 4.
સમાંતર શ્રેણી 9, 17, 25, ……….. નાં કેટલાં પદોનો સરવાળો 636 થાય?
ઉત્તરઃ
અહીં, a = 9; d = 17 – 9 = 8; S = 636; n =?
S_n = \(\frac{n}{2}\) [2a + (n – 1) d]
636 = \(\frac{n}{2}\) [18 + (n – 1)8]
636 = \(\frac{n}{2}\) [10 + 8n]
636 = n [4n + 55]
4n² + 5n – 636 = 0
હવે, a = 4; b = 5; c =- 636
b² – 4ac = (5)² – 4 (4) (- 636)
= 25 + 10176 = 10201
∴ \(\sqrt{b^{2}-4 a c}=\sqrt{10201}\) = 101

આથી n = \(\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)

n = \(\frac{-5 \pm 101}{8}\)

n = \(\frac{96}{8}\) અથવા n = \(-\frac{106}{8}\)
n = 12 અથવા n = – \(\frac{53}{4}\)
n એ પદનો ક્રમાંક દર્શાવતો હોવાથી ધન પૂર્ણાક જ હોય.
n = – \(\frac{53}{4}\) શક્ય નથી.
n = 12
આમ, આપેલ સમાંતર શ્રેણીનાં 12 પદોનો સરવાળો 636 થાય.

પ્રશ્ન 5.
સમાંતર શ્રેણીનું પ્રથમ પદ 5, અંતિમ પદ 45 અને સરવાળો 400 છે. શ્રેણીનાં પદોની સંખ્યા અને સામાન્ય તફાવત શોધો.
ઉત્તરઃ
અહીં, a = 5; l = 45; S_n = 400; n = ?; d =?
S_n = \(\frac{n}{2}\) (a + l)
400 = \(\frac{n}{2}\) (5 + 45)
800 = n (50)
n = 16
l = a_n = a + (n – 1) d
a₁₆ = a + 15d
45 = 5 + 15d
40 = 15d
d = \(\frac{40}{15}\)
d = \(\frac{8}{3}\)
આમ, આપેલ સાત્ત સમાંતર શ્રેણીમાં પદોની સંખ્યા 18 છે અને સામાન્ય તફાવત છે.

પ્રશ્ન 6.
સમાંતર શ્રેણીનાં પ્રથમ પદ અને અંતિમ પદ અનુક્રમે 17 અને 350 છે. જો સામાન્ય તફાવત 9 હોય, તો તેમાં કેટલાં પદ હશે અને તેમનો સરવાળો કેટલો થશે?
ઉત્તરઃ
અહીં, a = 17; l = a_n = 350; d = 9; n = ?; S_n = ?
a_n = a + (n – 1) d
350 = 17 + (n – 1) 9
333 = 9 (n – 1)
n – 1 = 37
∴ n = 38
હવે, S_n = \(\frac{n}{2}\) (a + l)
S₃₈ = \(\frac{38}{2}\) (17 + 350)
S₃₈ = 19 × 367
∴ S₃₈ = 6973
આમ, આપેલ સાત્ત સમાંતર શ્રેણીમાં કુલ 38 પદ છે અને ૬ બધાં જ પદોનો સરવાળો 6973 થાય છે.

પ્રશ્ન 7.
જે સમાંતર શ્રેણીમાં d = 7 અને 22મું પદ 149 હોય, તેનાં 22 પદોનો સરવાળો શોધો.
ઉત્તરઃ
અહીં, a₂₂ = 149; d = 7; S₂₂ = ?
a_n = a + (n – 1) d
a₂₂ = a + 21d
149 = a + 21 × 7
a = 149 – 147
a = 2
હવે, S_n = \(\frac{n}{2}\) (a + l)
S₂₂ = \(\frac{22}{2}\) (2 + 149)
S₂₂ = 11 × 151
S₂₂ = 1661
આમ, આપેલ સમાંતર શ્રેણીનાં પ્રથમ 22 પદોનો સરવાળો 1661 થાય.

પ્રશ્ન 8.
સમાંતર શ્રેણીનું બીજું અને ત્રીજું પદ અનુક્રમે 14 અને 18 હોય, તો તેનાં પ્રથમ 51 પદોનો સરવાળો શોધો.
ઉત્તરઃ
અહીં, a₂ = 14; a₃ = 18; S₅₁ = ?
a_n = a + (n – 1) d
a₂ = a + d = 14 ………. (1)
a₃ = a + 2d = 18 …………… (2)
સમીકરણ (1) અને (2) પરથી d = 4 અને 4 = 10 મળે.
S_n = \(\frac{n}{2}\) [2a + (n – 1) d]
S₅₁ = \(\frac{51}{2}\) [20 + 50 x 4]
S₅₁ = 51 × 110
S₅₁ = 5610
આમ, આપેલ સમાંતર શ્રેણીનાં પ્રથમ 51 પદોનો સરવાળો 5610 થાય.

પ્રશ્ન 9.
સમાંતર શ્રેણીનાં પ્રથમ 7 પદોનો સરવાળો 49 અને 17 પદોનો સરવાળો 289 હોય, તો તેનાં પ્રથમ ત પદોનો સરવાળો શોધો.
ઉત્તરઃ
અહીં, S₇ = 49; S₁₇ = 289; S_n = ?
S_n = \(\frac{n}{2}\) [2a + (n – 1) d]]
S₇ = \(\frac{n}{2}\) [2a + 6d]
49 = 7(a + 3d)
a + 3d = 7 …………… (1)
વળી, S₁₇ = \(\frac{17}{2}\) [2a + 16d]
289 = 17 (a + 8d)
a + 8d = 17 …………… (2)
સમીકરણ (1) અને (2) પરથી d = 2 અને 4 = 1 મળે.

S_n = \(\frac{n}{2}\) [2a + (n-1) d]
S_n = \(\frac{n}{2}\) [2 + (n – 1) 2]
S_n= \(\frac{n}{2}\) [2 + 2n – 2].
S_n = \(\frac{n}{2}\) (2n)
S_n = n²
આમ, આપેલ સમાંતર શ્રેણીનાં પ્રથમ 7 પદોનો સરવાળો n² મળે.

પ્રશ્ન 10.
a_n નીચે પ્રમાણે વ્યાખ્યાયિત છેઃ
(i) a_n = 3 + 4n
(ii) a_n = 9 – 5n
સાબિત કરો કે a₁, a₂, ………., a_n, …….. સમાંતર શ્રેણી બનાવે છે. વળી, દરેકમાં પ્રથમ 15 પદોનો સરવાળો શોધો.

(i) a_n = 3+ 4n
a₁ = 3 + 4 (1) = 7,
a₂ = 3+ 4 (2) = 11,
a₃ = 3 + 4 (3) = 15,
a₄ = 3 + 4 (4) = 19, ………
અહીં, a₄ – a₃ = a₃ – a₂ = a₂ – a₁ = 4. આમ, a_k+1 – a_k હંમેશાં સમાન રહે છે.
થી a_n = 3 + 4n દ્વારા વ્યાખ્યાયિત થતાં a₁, a₂, ………., a_n, …….. સમાંતર શ્રેણી રચે છે, જેમાં a = 7 અને d = 4.
S_n = \(\frac{n}{2}\) [2a + (n – 1) d]
S₁₅ = \(\frac{15}{2}\) [14 + 14 × 4]
S₁₅ = 15 × 35
S₁₅ = 525
આમ, a_n = 3 + 4n
દ્વારા વ્યાખ્યાયિત થતી સમાંતર શ્રેણીનાં પ્રથમ 15 પદોનો સરવાળો 525 થાય.

(ii) a_n = 9 – 5n
a₁ = 9 – 5 (1) = 4,
a₂ = 9 – 5 (2) = – 1,
a₃ = 9 – 5 (3) =- 6,
a₄ = 9 – 5 (4) = – 11, ……..
અહીં, a₄ – a₃ = a₃ – a₂ = a₂ – a₁ = – 5. આમ, a_k+1 – a_k હંમેશાં સમાન રહે છે.
આથી a_n = 9 – 5n દ્વારા વ્યાખ્યાયિત થતાં a₁, a₂, ………., a_n, …….. સમાંતર શ્રેણી રચે છે, જેમાં a = 4 અને d = – 5.
S_n = \(\frac{n}{2}\) [2a + (n – 1) d)
S₁₅ = \(\frac{15}{2}\) [8 + 14(- 5)]
S₁₅ = \(\frac{15}{2}\) (- 62).
S₁₅ = 15 × (- 31) :
S₁₅ = – 465
આમ, a_n = 9 – 5n દ્વારા વ્યાખ્યાયિત થતી સમાંતર શ્રેણીનાં પ્રથમ 15 પદોનો સરવાળો – 465 થાય.

પ્રશ્ન 11.
સમાંતર શ્રેણીનાં પ્રથમ ૧ પદોનો સરવાળો 4n – n² હોય, તો તેનું પ્રથમ પદ કર્યું હશે (અર્થાત્ sp? પ્રથમ બે પદોનો સરવાળો કેટલો હશે? બીજું પદ કર્યું હશે? આ જ રીતે ત્રીજું, 10મું અને તમું પદ શોધો.
ઉત્તરઃ
આપેલ સમાંતર શ્રેણી માટે,
S_n = 4n – n²
S₁ = 4(1) – (1)² = 4 – 1 = 3,
S₂ = 4 (2) – (2)² = 8 – 4 = 4,
S₃ = 4(3) – (3)² = 12 – 9 = 3,
S₉ = 4 (9) – (9)² = 36 – 81 = – 45,
S₁₀ = 4(10) – (10)² = 40 – 100 = – 60
હવે, પ્રથમ પદ = a = a₁ = S₁ = 3
પ્રથમ બે પદોનો સરવાળો S₂ = 4.
બીજું પદ a₂ = S₂ – S₁ = 4 – 3 = 1
ત્રીજું પદ a₃ = S₃ – S₂ = 3 – 4 = – 1
10મું પદ a₁₀ = S₁₀ – S₉ = – 60 – (45) = – 15
હવે, S_n = 4n – n²
S_n – 1= 4(n – 1) – (n – 1)²
= 4n – 4 – n² + 2n – 1
= – n² + 6n – 5
હવે,nમું પદ a_n = S_n – n – 1
a_n = (4n – n²) – (- n² + 6n – 5)
a_n = 4n – n² + n² – 6n + 5
a_n = – 2n + 5

પ્રશ્ન 12.
6 વડે વિભાજ્ય પ્રથમ 40 ધન પૂર્ણાકોનો સરવાળો શોધો. 6 વડે વિભાજ્ય પ્રથમ 40 ધન પૂર્ણાકો નીચે મુજબની સાન્ત સમાંતર શ્રેણી રચે: 6, 12, 18, ………., 240.
ઉત્તરઃ
અહીં, a = 6; d = 12 – 6 = 6; n = 40 અને l = 240.
S_n = \(\frac{n}{2}\) (a + l)
S₄₀ = \(\frac{40}{2}\) (6 + 240)
S₄₀ = 20 × 246
S₄₀ = 4920
આમ, માગેલ સરવાળો 4920 થાય.

વૈકલ્પિક રીતઃ
માગેલ સરવાળો = 6 + 10 + 18 + … + 240
= 6 (1 + 2 + 3 + … + 40)
= 6 × \(\frac{40 \times 41}{2}\) (1 + 2 + 3 + …………. + n = \(\frac{n(n+1)}{2}\))
= 4920

પ્રશ્ન 13.
8ના પ્રથમ 15 ગુણિતોનો સરવાળો શોધો. 8ના પ્રથમ 15 ગુણિતો નીચે મુજબની સાન્ત સમાંતર શ્રેણી રચે: 8, 16, 24, ……….., 120.
ઉત્તરઃ
અહીં, a = 8; d = 16 – 8 = 8; n = 15 અને l = 120.
S_n = \(\frac{n}{2}\) (a + l)
S₁₅ = \(\frac{15}{2}\) (8 + 120)
S₁₅ = 15 × 64
S₁₅ = 960
આમ, માગેલ સરવાળો 960 થાય.

વૈકલ્પિક રીતઃ
માગેલ સરવાળો = 8 + 16 + 24 + … + 120
= 8 (1 + 2 + 3 + … + 15)
= 8 × \(\frac{15 \times 16}{2}\) (1 + 2 + 3 + ………. + n = \(\frac{n(n+1)}{2}\))
= 960.

પ્રશ્ન 14.
0 અને 50 વચ્ચેના અયુગ્મ પૂર્ણાકોનો સરવાળો શોધો. 0 અને 50 વચ્ચેના અયુગ્મ પૂર્ણાકો નીચે મુજબની સાન્ત સમાંતર શ્રેણી રચે: 1, 3, 5, ……………, 49.
ઉત્તરઃ
અહીં, a = 1; d = 3 – 1 = 2; l = 49.
ધારો કે, અંતિમ પદ એ શ્રેણીનું nમું પદ છે.
a_n = a + (n – 1) d
49 = 1 + (n – 1) 2
2 (n – 1) = 48
n – 1 = 24
n = 25
હવે, S_n = \(\frac{n}{2}\) (a + l)
S₂₅ = \(\frac{25}{2}\) (1 + 49)
S₂₅ = 25 × 25
S₂₅ = 625
આમ, માગેલ સરવાળો 625 થાય.

પ્રશ્ન 15.
નિર્માણ કામ માટે થયેલ કરારમાં નિશ્ચિત તારીખ કરતાં વિલંબથી પૂરા થતા કામ માટે નીચે પ્રમાણેના દંડની જોગવાઈ છેઃ પ્રથમ દિવસ માટે ₹ 200, બીજા દિવસ માટે ₹ ₹ 250, ત્રીજા દિવસ માટે ₹ 300, વગેરે. પ્રત્યેક દિવસ માટે દંડની રકમ આગળના દિવસ કરતાં ₹ 50 વધુ છે. જો કૉન્ટ્રાક્ટર 30 દિવસનો વિલંબ કરે, તો તેણે ભરવી પડતી દંડની રકમ શોધો.
ઉત્તરઃ
પ્રત્યેક દિવસ માટેની દંડની રકમ (મ) નીચે મુજબની સમાંતર શ્રેણી રચે છે :
200, 250, 300, ……….
અહીં, a = 200; d = 250 – 200 = 50 અને કૉન્ટ્રાક્ટરે 30 દિવસનો વિલંબ કરેલ હોવાથી n = 30 લેવાથી મળતા S₃₀ જેટલી દંડની રકમ તેણે ભરવી પડે.
S_n = \(\frac{n}{2}\) [2a + (n – 1) d]
S₉₀ = \(\frac{30}{2}\) [400 + (30 – 1) 50]
S₉₀ = 15 × 1850
S₉₀ = 27750
આમ, કૉન્ટ્રાક્ટરે ભરવી પડતી દંડની રકમ ₹ 27,750 થાય.

પ્રશ્ન 16.
કોઈ એક શાળામાં વિદ્યાર્થીઓના સમગ્ર શૈક્ષણિક પ્રદર્શન માટે અપાતા 7 ઇનામો માટે કુલ ર700ની જોગવાઈ કરવાની છે. જો પ્રત્યેક ઇનામ આગળના ઇનામ કરતાં 20 ઓછું હોય, તો પ્રત્યેક ઇનામની રકમ શોધો.
ઉત્તરઃ
કુલ ₹ 700 સાત ઇનામોમાં વહેંચવાના છે.
જેથી પ્રત્યેક ઇનામ આગળના ઇનામ કરતાં ₹ 20 ઓછું હોય. ધારો કે સૌથી મોટું ઇનામ, એટલે કે પહેલું ઈનામ ₹ a નું છે.
આથી બીજું ઇનામ ₹ a – 20નું, ત્રીજું ઈનામ ₹ a – 40નું એમ કુલ સાત ઈનામો થાય.
આમ, આ ઈનામોમાં અપાતી રકમ (સમાં) નીચે પ્રમાણેની સાન્ત સમાંતર શ્રેણી રચે :
a, a – 20, a – 40, a – 60, a – 80, a – 100 અને a – 120.
અહીં, પ્રથમ પદ = a; d = (a – 20) – a = – 20; n = 7 અને બધાં 7 પદોનો સરવાળો = S₇ = 700.
S_n = \(\frac{n}{2}\) [2a + (n-1) d]
700 = \(\frac{7}{2}\) [2a + (7 – 1) (- 20)].
200 = 2a + 6 (- 20).
200 = 2a – 120
2a = 320
a = 160
આથી a – 20 = 140;
a – 40 = 120;
a – 60 = 100;
a – 80 = 80;
a – 100 = 60
અને a – 120 = 40.
આમ, પ્રત્યેક ઇનામની રકમ (માં) ઊતરતા ક્રમે 160, 140, 120, 100, 80, 60 અને 40 છે.

પ્રશ્ન 17.
એક શાળામાં વિદ્યાર્થીઓ વાયુ-પ્રદૂષણ ઓછું કરવા માટે શાળાની અંદર અને બહાર વૃક્ષ વાવવાનું વિચારે છે. એવું નક્કી કરાયું કે પ્રત્યેક ધોરણનો પ્રત્યેક વિભાગ તે જે ધોરણમાં ભણતા હોય તેટલાં વૃક્ષ વાવશે. દાખલા તરીકે ધોરણ નો વિભાગ 1 વૃક્ષ, ધોરણ II નો વિભાગ 2 વૃક્ષ અને આવું ધોરણ xII સુધી ચાલશે. દરેક ધોરણમાં ત્રણ વિભાગ છે. આ વિદ્યાર્થીઓ દ્વારા કેટલાં વૃક્ષનું વાવેતર થશે?
ઉત્તરઃ
ધોરણ ના ત્રણ વિભાગના વિદ્યાર્થીઓ = 1 + 1 + 1 = 3 વૃક્ષોનું વાવેતર કરશે.
ધોરણ Iના ત્રણ વિભાગના વિદ્યાર્થીઓ = 2 + 2 + 2 = 6 વૃક્ષોનું વાવેતર કરશે.
આ જ રીતે આગળ વધતાં,
ધોરણ XII ના ત્રણ વિભાગના વિદ્યાર્થીઓ = 12 + 12 + 12 = 36 વૃક્ષોનું વાવેતર કરશે.
આમ, વાવેતર થતાં વૃક્ષોની સંખ્યા નીચે મુજબની સાન સમાંતર શ્રેણી રચે : 3, 6, 9, …, 36.
અહીં, વ = 3; d = 6 – 3 = 3; n = 12 અને S₁₂ ની કિંમત વિદ્યાર્થીઓ દ્વારા કેટલાં વૃક્ષનું વાવેતર થશે તે સંખ્યા આપે.

S_n = \(\frac{n}{2}\) [2a + (n – 1) d]
S₁₂ = \(\frac{12}{2}\) [6 + (12 – 1) 3]
S₁₂ = 6 × 39
S₁₂ = 234
આમ, શાળાના વિદ્યાર્થીઓ દ્વારા 234 વૃક્ષનું વાવેતર થશે.

પ્રશ્ન 18.
વારાફરતી A અને Bને કેન્દ્ર લઈ ક્રમિક અર્ધવર્તુળોની મદદથી એક કુંતલ (Spiral) બનાવેલ છે. તેની શરૂઆત Aથી થાય છે. આકૃતિમાં દર્શાવ્યા પ્રમાણે ત્રિજ્યાઓ 0.5 સેમી, 1.0 સેમી, 1.5 સેમી, 2.0 સેમી, , હોય, તો આવા 13 ક્રમિક અર્ધવર્તુળોથી બનતા કુંતલની લંબાઈ શોધો. (π = \(\frac{22}{7}\) લો.)

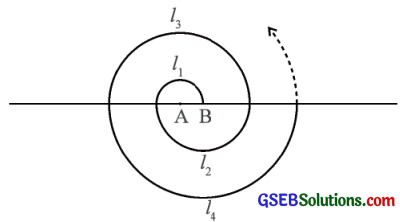
[સૂયન: ક્રમિક અર્ધવર્તુળની લંબાઈ l₁, l₂, l₃, l₄, ………. અને : કેન્દ્રો અનુક્રમે A, B, A, B, ……….. છે.].
ઉત્તરઃ
અર્ધવર્તુળની લંબાઈ = πr, જ્યાં 1 ત્રિજ્યા છે.
A કેન્દ્ર અને 0.5 સેમી ત્રિજ્યાવાળા પહેલાં અર્ધવર્તુળની લંબાઈ = l = π × 0.5 સેમી.
B કેન્દ્ર અને 1 સેમી ત્રિજ્યાવાળા બીજાં અર્ધવર્તુળની લંબાઈ = 9 = π × 1 સેમી.
A કેન્દ્ર અને 1.5 સેમી ત્રિજ્યાવાળા ત્રીજા અર્ધવર્તુળની લંબાઈ = 3 = π × 1.5 સેમી.
આ રીતે આગળ વધતા, A કેન્દ્ર અને 6.5 સેમી ત્રિજ્યાવાળા 13મા અર્ધવર્તુળની લંબાઈ = l₁₃ = π × 6.5 સેમી.
હવે, 13 ક્રમિક અર્ધવર્તુળોથી બનતા કુંતલની લંબાઈ
= l₁ + l₂ + l₃ + ……… + l₁₃
= (π × 0.5) + (π × 1) + (π × 1.5) + …….. + (π × 6.5)
= π (0.5 + 1 + 1.5 + ……. + 6.5).
અહીં, કૌસમાં આપેલ સરવાળો એ 13 પદ ધરાવતી સાન્ત શ્રેણીનાં પદોનો સરવાળો છે.
આ સાત્ત સમાંતર શ્રેણી માટે,
a = 0.5, d = 1 – 0.5 = 0.5 અને n = 13.
S_n = \(\frac{n}{2}\) [2a + (n – 1)d]
S_n = \(\frac{13}{2}\) [1 + (13- 1) (0.5)]
S_n = \(\frac{13}{2}\) × 7

આમ, કુંતલની લંબાઈ = 1 (\(\frac{13}{2}\) × 7)
= \(\frac{22}{7}\) × \(\frac{13}{2}\) × 7
= 143 સેમી
આમ, 13 ક્રમિક અર્ધવર્તુળોથી બનતા કુંતલની લંબાઈ 143 સેમી છે.

પ્રશ્ન 19.
લાકડાની 200 ભારીઓ નીચે પ્રમાણે ગોઠવવામાં આવે છે : તળિયાની હારમાં 20 ભારી, તેની ઉપરની હારમાં 19 ભારી, તેની ઉપરની હારમાં 18 ભારીઓ વગેરે (જુઓ આકૃતિ).

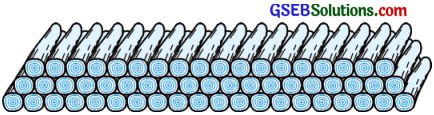
આવી 200 ભારીઓ ગોઠવવા માટે કેટલી હાર થશે અને સૌથી ઉપરની હારમાં કેટલી ભારીઓ થશે?
ઉત્તરઃ
સૌથી નીચેની હારમાં ગોધેલ ભારીની સંખ્યા = 20.
નીચેથી બીજી હારમાં ગોઠવેલ ભારીની સંખ્યા = 19.
નીચેથી ત્રીજી હારમાં ગોઠવેલ ભારીની સંખ્યા = 18.
આ મુજબ 200 ભારીઓ ગોઠવાઈ જાય તેટલી હાર બનાવવામાં આવે છે.
આથી હારદીઠ ગોઠવાતી ભારીઓની સંખ્યા સાન્ત સમાંતર શ્રેણી 20, 19, 18, ………., n પદ સુધી બનાવે છે, જેમાં n પદોનો સરવાળો 200 થાય.
અહીં, a = 20 અને d = 19 – 20 = – 1.
S_n = \(\frac{n}{2}\) [2a + (n -1 )d]
200 = \(\frac{n}{2}\) [40 + (n – 1) (- 1)]
400 = n (40 – n + 1)
400 = n (41 – n)
400 = 41 n – n²
n² – 41 n + 400 = 0
n² – 167 – 25n + 400 = 0
n(n – 16) – 25 (n – 16) = 0
(n – 16) (n – 25) = 0
n – 16 = 0 અથવા n – 25 = 0
n = 16 અથવા n = 25
અહીં, ગાણિતિક રીતે બને જવાબ શક્ય છે. આથી આપણે 16મું પદ અને 25મું પદ શોધીને નિર્ણય લઈએ.
a_n = a + (n – 1)d
a₁₆ = 20 + 15(-1) = 5
a₂₅ = 20 + 24(-1 ) = – 4
આમ, 25મી હારમાં મુકાતી ભારીઓની સંખ્યા ઋણ થાય છે, જે શક્ય નથી.
∴ n = 16 અને a₁₆ = 5
આમ, 200 ભારીઓ ગોઠવવા માટે કુલ 16 હાર બનશે અને સૌથી ઉપરની હારમાં 5 ભારીઓ મુકાશે.

પ્રશ્ન 20.
એક બટાકા ઉપાડવાની હરીફાઈમાં આરંભબિંદુ પર એક ડોલ રાખેલ છે અને ત્યારબાદ તેનાથી 5 મી દૂર પ્રથમ બટાકું મૂકેલ છે. ત્યારપછી દર ત્રણ મીટરે એક બટાકું સીધી રેખામાં ગોઠવેલ છે. આવા 10 બટાકા રેખા પર મૂકેલ છે. (જુઓ આકૃતિ)

3 મી 8મી દરેક હરીફે ડોલ પાસેથી દોડી પોતાની નજીકનું બટાકું ઉપાડી, પાછા આવી ડોલમાં નાખવાનું છે. ત્યારબાદ આ જ પ્રમાણે બીજું, ત્રીજું એમ છેલ્લું બટાકું ડોલમાં મુકાય ત્યાં સુધી દોડવાનું છે. હરીફે કેટલું અંતર દોડવું પડે?
[સૂચનઃ પ્રથમ અને દ્વિતીય બટાકું ઉપાડવા હરીફ દ્વારા કપાતું અંતર (મીટરમાં) 2 × 5 + 2 × (5 + 3)].
ઉત્તરઃ
પ્રથમ બટાકું ઉપાડવા હરીફ દ્વારા કપાતું અંતર (મીટરમાં) = 2 × 5 = 10
દ્વિતીય બટાકું ઉપાડવા હરીફ દ્વારા કપાતું અંતર (મીટરમાં) = 2 × (5 + 3) = 16
તૃતીય બટાકું ઉપાડવા હરીફ દ્વારા કપાતું અંતર (મીટરમાં) = 2 × (5 + 3 + 3) = 22.
આમ, 10 બટાકા ઉપાડવા માટે હરીફ દ્વારા કપાતું અંતર 10 પદની સાન્ત સમાંતર શ્રેણી
10, 16, 22, …………, 10 પદ સુધી બનાવે છે.
અહીં, a = 10; d = 16 – 10 = 6; n = 10 અને S_n હરીફ દ્વારા કપાતું કુલ અંતર (મીટરમાં) દર્શાવે.
S_n = \(\frac{n}{2}\) [2a + (n – 1)d]
S₁₀ = \(\frac{10}{2}\) [20 + (10 – 1)6]
S₁₀ = 5 × 74
S₁₀ = 370
આમ, હરીફે કુલ 370 મીટર અંતર દોડવું પડે.