Gujarat Board GSEB Solutions Class 10 Maths Chapter 7 યામ ભૂમિતિ Ex 7.3 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 10 Maths Chapter 7 યામ ભૂમિતિ Ex 7.3
પ્રશ્ન 1.
જેનાં શિરોબિંદુઓ નીચે પ્રમાણે છે તેવા ત્રિકોણનું ક્ષેત્રફળ શોધોઃ
(i) 2, 3), (- 1, 6), (2, – 4)
(ii) (- 8, – 1), (3, – 5), (5, 2).
ઉત્તરઃ
(i) ધારો કે, ∆ ABCનાં શિરોબિંદુઓ A (2, 3), B(- 1, 0) અને C (2, – 4) છે.
ક્ષેત્રફળ સૂત્રનો ઉપયોગ કરતાં,
∆ ABCનું ક્ષેત્રફળ = \(\frac{1}{2}\) [2 (0 + 4) + (- 1) (- 4 – 3) + 2 (3 – 0)
= \(\frac{1}{2}\) (8 + 7 + 6)
= \(\frac{21}{2}\) ચોરસ એકમ
આમ, આપેલ શિરોબિંદુઓવાળા ત્રિકોણનું ક્ષેત્રફળ \(\frac{21}{2}\) ચોરસ એકમ છે.

(ii) આપેલ ત્રિકોણનાં શિરોબિંદુઓ (- 5, – 1), (3, – 5) અને (5, 2) છે.
ક્ષેત્રફળ સૂત્રનો ઉપયોગ કરતાં, આપેલ ત્રિકોણનું ક્ષેત્રફળ =\(\frac{1}{2}\) [- 5(- 5 – 2) + 3 (2 + 1) + 5(- 1+ 5)].
= \(\frac{1}{2}\) (35 + 9 + 20) = \(\frac{1}{2}\) (64)
= 32 ચોરસ એકમ
આમ, આપેલ શિરોબિંદુઓવાળા ત્રિકોણનું ક્ષેત્રફળ 32 ચોરસ એકમ છે.
પ્રશ્ન 2.
નીચે આપેલાં બિંદુઓ સમરેખ હોય તો પ્રત્યેકમાં ‘k’ ની કિંમત શોધોઃ
(i) (7, – 2), (5, 1), (3, k)
(ii) (8, 1), (k, – 4), (2, – 3)
ઉત્તરઃ
(1) જો બિંદુઓ (7, – 2), (5, 1) અને (3, k) સમરખ હોય, તો તેમના દ્વારા બનતા કાલ્પનિક ત્રિકોણનું ક્ષેત્રફળ શૂન્ય જ થાય.
\(\frac{1}{2}\) [7 (1 – k) + 5 (k + 2) + 3(- 2 – 1)] = 0
\(\frac{1}{2}\) (7 – 7k + 5k + 10 – 9) = 0
– 2k + 8 = 0
∴ 2k = 8
∴ k = 4

(ii) જો બિંદુઓ (8, 1), (k, – 4) અને (2, – 5) સમરેખ હોય, તો તેમના દ્વારા બનતા કાલ્પનિક ત્રિકોણનું ક્ષેત્રફળ શુન્ય જ થાય. .
\(\frac{1}{2}\) [8 (- 4 + 5) + k(- 5 – 1) + 2 (1 + 4)] = 0.
8 – 6k + 10 = 0
18 = 6k
k = 3
પ્રશ્ન 3.
જેનાં શિરોબિંદુઓ (0,- 1), (2, 1) અને (0, 3) હોય, તેવા ત્રિકોણની બાજુઓનાં મધ્યબિંદુઓને જોડવાથી બનતા ત્રિકોણનું ક્ષેત્રફળ શોધો. આ ત્રિકોણનું ક્ષેત્રફળ અને આપેલ ત્રિકોણના ક્ષેત્રફળનો ગુણોત્તર શોધો.
ઉત્તરઃ
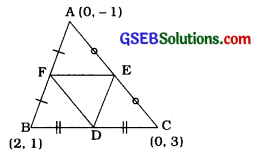
ધારો કે, A (0, – 1), B (2, 1) અને C (0, 3) એ આપેલ ત્રિકોણનાં શિરોબિંદુઓ છે તથા D, E અને F એ અનુક્રમે BC, CA અને AB નાં મધ્યબિંદુઓ છે.
હવે, D ના યામ = \(\left(\frac{2+0}{2}, \frac{1+3}{2}\right) \) = (1, 2)
E ના ધામ = \(\left(\frac{0+0}{2}, \frac{3-1}{2}\right)\) = (0, 1)
Fના યામ = \(\left(\frac{0+2}{2}, \frac{-1+1}{2}\right)\) = (1, 0)
∆ DEFનું ક્ષેત્રફળ = \(\frac{1}{2}\) [1 (1 – 0) + 0 (0 – 2) + 1 (2 – 1)].
= \(\frac{1}{2}\) (1 + 0 + 1) = 1 ચોરસ એકમ
∆ ABCનું ક્ષેત્રફળ = \(\frac{1}{2}\) [0 (1 – 3) + 2(3 + 1) + 0(- 1 – 1)] =
= \(\frac{1}{2}\) (0 + 8 + 2) = 4 ચોરસ એકમ
આથી ∆ DEFનું ક્ષેત્રફળ: ABCનું ક્ષેત્રફળ = 1 : 4
આમ, આપેલ શિરોબિંદુઓવાળા ત્રિકોણની બાજુઓનાં મધ્યબિંદુઓને જોડવાથી મળતા ત્રિકોણનું ક્ષેત્રફળ ચોરસ એકમ થાય અને માગેલ ગુણોત્તર 1 : 4 થાય.

પ્રશ્ન 4.
એક ચતુષ્કોણનાં ક્રમિક શિરોબિંદુઓ (- 4, – 2), (- 3, – 5), (3, – 2) અને (2, 3) હોય, તો તેનું ક્ષેત્રફળ શોધો.
ઉત્તરઃ
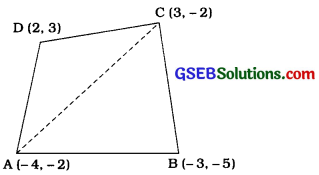
ધારો કે, A(- 4, – 2), B(- 3, – 5), C (3, – 2) અને D (2, 3) આપેલ ચતુષ્કોણ ABCDનાં શિરોબિંદુઓ છે.
વિકર્ણ AC દોરવાથી આપણને બે ત્રિકોણો ∆ ABC અને ADC મળે. ∆ ABCનાં શિરોબિંદુઓ A(- 4, – 2), B(- 3, – 5) અને C (3, – 2) છે.
∆ ABCનું ક્ષેત્રફળ
= \(\frac{1}{2}\) [- 4(- 5 + 2) + (- 3) (- 2 + 2) + 3 (- 2 + 5)]
= \(\frac{1}{2}\) (12 + 0 + 9)
= \(\frac{21}{2}\) ચોરસ એકમ
∆ ADCનાં શિરોબિંદુઓ A(- 4, – 2), D (2, 3) અને C (3, – 2) છે.
∆ ADCનું ક્ષેત્રફળ
= \(\frac{1}{2}\) [- 4 (3 + 2) + 2 (- 2 + 2) + 3(- 2 – 3)]
= \(\frac{1}{2}\) (- 20 + 0 – 15)
= \(\frac{1}{2}\) (- 35)
પરંતુ, ત્રિકોણનું ક્ષેત્રફળ કદી ઋણ ન હોય. આથી આપણે સંખ્યાત્મક કિંમત લઈશું.
∆ ADCનું ક્ષેત્રફળ = \(\frac{35}{2}\) ચોરસ એકમ
હવે, ચતુષ્કોણ ABCDનું ક્ષેત્રફળ = ∆ ABCનું ક્ષેત્રફળ + ∆ ADCનું ક્ષેત્રફળ
= (\(\frac{21}{2}+\frac{35}{2}\)) ચોરસ એકમ = 28 ચોરસ એકમ
આમ, આપેલ ચતુષ્કોણનું ક્ષેત્રફળ 28 ચોરસ એકમ છે.

પ્રશ્ન 5.
તમે ધોરણ IX(પ્રકરણ 9, પ્રશ્ન નં. ૩)માં શીખ્યા છો કે ત્રિકોણની મધ્યગા ત્રિકોણનું બે સમાન ક્ષેત્રફળવાળા ત્રિકોણમાં વિભાજન કરે છે. જેનાં શિરોબિંદુઓ A (4, – 6), B (3, – 2) અને C (5, 2) હોય તેવ ∆ ABC માટે આ પરિણામ ચકાસો.
ઉત્તરઃ
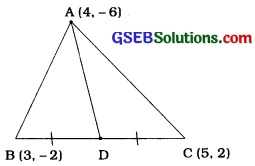
ધારો કે, A (4, – 6), B (3, – 2) અને C (5, 2) એ ∆ ABCનાં શિરોબિંદુઓ છે તથા AD મધ્યગા છે.
આથી D એ BCનું મધ્યબિંદુ છે.
∴ Dના ધામ \(\left(\frac{3+5}{2}, \frac{-2+2}{2}\right)\), એટલે કે (4, o) થાય.
∆ ABCનું ક્ષેત્રફળ
= \(\frac{1}{2}\) [4 (- 2 – 2) + 3 (2 + 6) + 5 (- 6 + 2)]
= \(\frac{1}{2}\) [- 16 + 24- 20]
= \(\frac{1}{2}\) (- 12) = 8 ચોરસ એકમ ( ક્ષેત્રફળ ઋણ ન હોય.) …… (1)
∆ ADBનાં શિરોબિંદુઓ A (4, – 6), D (4, 4) અને B (3, – 2) છે.
∆ ADBનું ક્ષેત્રફળ = \(\frac{1}{2}\)[ [4 (0 + 2) + 4(- 2 + 6) + 3(- 6 – 0)].
= \(\frac{1}{2}\) [8 + 16 – 18] = 3 ચોરસ એકમ ……………… (2)
∆ ADCનાં શિરોબિંદુઓ A (4, – 6), D (4, 4) અને C (5, 2) છે.
∆ ADCનું ક્ષેત્રફળ
= \(\frac{1}{2}\) [4 (0, – 2) + 4 (2 + 6) + 5 (- 6 – 0))
= \(\frac{1}{2}\) (- 8 + 32 – 30) = \(\frac{1}{2}\) (- 6)
= 3 ચોરસ એકમ (.. ક્ષેત્રફળ ઋણ ન હોય.) ……. (3)
(1), (2) અને (3) પરથી, ∆ ADBનું ક્ષેત્રફળ = ∆ ADCનું ક્ષેત્રફળ
= \(\frac{1}{2}\) ∆ ABCનું ક્ષેત્રફળ
આમ, મધ્યગા AD દ્વારા ∆ ABCનું બે સમાન ક્ષેત્રફળ ધરાવતા ત્રિકોણો, ∆ ADB અને ∆ ADCમાં વિભાજન થાય છે.
આ પ્રમાણે જ, મધ્યગાઓ BE અને CF માટે પણ ઉપરોક્ત પરિણામ સાબિત કરી શકાય.
આમ, “ત્રિકોણની મધ્યમા ત્રિકોણનું બે સમાન ક્ષેત્રફળવાળા ત્રિકોણમાં વિભાજન કરે છે.” એ વિધાન સત્ય પુરવાર થાય છે.