Gujarat Board Statistics Class 11 GSEB Solutions Chapter 3 केन्द्रीय स्थिति के माप Ex 3.1 Textbook Exercise Questions and Answers.
Gujarat Board Textbook Solutions Class 11 Statistics Chapter 3 केन्द्रीय स्थिति के माप Ex 3.1
प्रश्न 1.
एक नर्सरी में बोये गए पौधों की सप्ताह के दौरान वृद्धि (से.मी.में ) निम्नानुसार है ।
1.0, 3.2, 1.4, 1.8, 1.6, 2.4, 1.4, 2.2, 1.3, 1.5 माध्य ज्ञात. करो ।
उत्तर :
यहाँ n = 10
माध्य = \(\frac{\sum x}{n}\)
∴ \(\bar{X}\) = 1.78 सेमी
नर्सरी में सप्ताह के दौरान पौधों की वृद्धि का माध्य = 1.78
प्रश्न 2.
एक रीले रेस में 4 स्पर्धकों की उम्र का माध्य 24 वर्ष गिना गया था। बाद में पता चला कि एक स्पर्धक की उम्र 27 वर्ष की थी, लेकिन उसके स्थान पर 25 वर्ष गलति से लिखा गया था । यदि उम्र का माध्य 25 वर्ष से अधिक हो तो स्पर्धा में हिस्सा नहीं ले सकता ऐसा नियम हो तो सुधार करने के बाद भी वह स्पर्धा में हिस्सा ले सकता है ।
उत्तर :
यहाँ n = 4 और माध्य 24 लेकर प्रथम योग ज्ञात करेंगे ।
∴ \(\bar{X}=\frac{\sum x}{n}\)
24 = \(\frac{\sum x}{4}\)
∴ 24 × 4 = Σx ∴ Σx = 96
अब गलत 25 उम्र लिखी गई थी और सही उम्र 27 वर्ष थी, इसलिए सही योग = 96 + 27 – 25 = 98
नया योग का माध्य = \(\frac{98}{4}\) = 24.5 वर्ष
उम्र 25 वर्ष से कम है इसलिए स्पर्धा में हिस्सा ले सकता है ।
प्रश्न 3.
एक थोक में से चयन किया विविध स्क्रू का व्यास (मिमि.) में निम्नानुसार है । स्क्रू के व्यास का माध्य ज्ञात करो ।
उत्तर :
यहाँ चल x की 6 किमत है ।
माध्य ज्ञात करने के लिए निम्नानुसार सारणी बनायेंगे । दिया आवृत्ति वितरण असतत (खंडित है) इसलिए प्रत्यक्ष विधि का उपयोग करेंगे ।
| x | f | fx |
| 30 | 4 | 120 |
| 35 | 10 | 350 |
| 40 | 15 | 600 |
| 45 | 8 | 360 |
| 50 | 5 | 250 |
| 55 | 3 | 165 |
| कुल | 45 | 1845 |
∴ माध्य \(\bar{X}=\frac{\sum f x}{n}=\frac{1845}{45}\)
∴ माध्य \(\bar{X}\) = 41 मि.मि.
स्क्रू के व्यास का माध्य \(\bar{X}\) = 41 होगा ।
प्रश्न 4.
विद्यार्थियों के एक समूह की कसौटी के गुण (नंबर ) निम्नानुसार है । विद्यार्थियों के गुण का माध्य ज्ञात करो ।
उत्तर :
वर्ग लंबाई c = 10 है इसलिए संक्षिप्त विधि d = \(\frac{x-\mathrm{A}}{\mathrm{C}}\) लेंगे । मध्यकिंमत = 
का उपयोग करके मध्यकिंमत प्राप्त करेंगे । माध्य की गणना के लिए निम्न सारणी में प्रस्तुत करेंगे ।
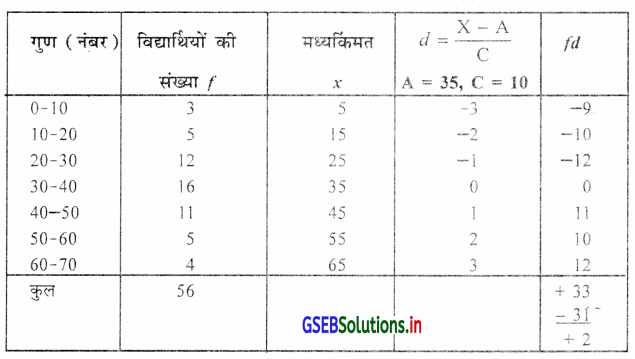
∴ माध्य \(\bar{X}\) = A + \(\frac{\sum f d}{n}\) × C = 35 + \(\frac{2}{56}\) × 10
= 35 + \(\frac{20}{56}\) = 35 + 0.36 = 35.36
∴ माध्य \(\bar{X}\) = 35.36 गुण (नंबर)
विद्यार्थियों के गुण (नंबर) का माध्य = 35.36 गुण है ।
प्रश्न 5.
एक मोबाइल धारक के पंजीकृत 254 कोल की बातचीत का समय (Talk Time) की सूचना निम्नानुसार है । बातचीत के समय का माध्य ज्ञात करो ।
उत्तर :
सारणी ‘से कम’ प्रकार का संचयी आवृत्ति वितरण दर्शाता है । क्रमानुसार वर्गों की आवृत्तिओं को घटाने पर संचयी आवृत्ति वितरण पर से मूल आवृत्ति वितरण प्राप्त करेंगे । प्रथम वर्ग की अधःसीमा = 0 बनेगी।
निम्नानुसार आवृत्ति वितरण प्राप्त करके d = \(\frac{\mathrm{x}-\mathrm{A}}{\mathrm{C}}\) का उपयोग करके माध्य ज्ञात करेंगे ।
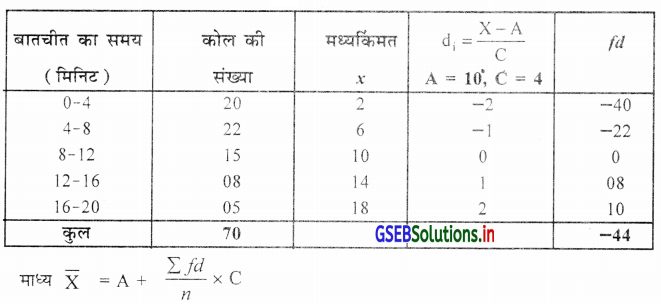
= 10 + \(\frac{-44}{70}\) × 4 = 10 – \(\frac{176}{70}\)
= 10 – 2.51
∴ माध्य = 7.49 मिनिट
बातचीत (Talk Time) का माध्य \(\bar{X}\) = 7.49 मिनिट
प्रश्न 6.
50 पीढ़ियों का पिछले वर्ष में हुए लाभ (लाख रु. में) का विवरण निम्नानुसार है । लाभ का माध्य ज्ञात कीजिए ।
उत्तर :
वर्गलंबाई 7 समान है इसलिए d = \(\frac{X-A}{C}\) का उपयोग करेंगे; मध्यमूल्य प्राप्त करेंगे ।
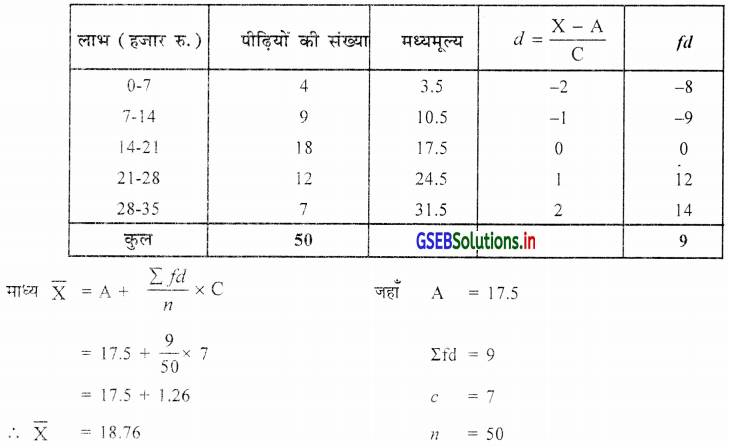
50 पीढ़ियों का पिछले वर्ष का लाभ का माध्य \(\overline{\mathrm{x}}\) = 18.76 हजार रु. होगा ।
प्रश्न 7.
एक वस्तु की विविध दिनों की माँग का वितरण निम्नानुसार है । माँग का माध्य ज्ञात करो ।
उत्तर :
आवृत्ति वितरण में असमान वर्गलंबाई है इसलिए प्रत्येक वर्ग की मध्यकिमत प्राप्त करके प्रत्यक्षविधि का सूत्र से माध्य प्राप्त करेंगे।
मध्यकिंमत = 
9.5, 19.5, 29.5, 42, 57, 72
| माँग (इकाई) | मध्यकिंमत x | f | fx |
| 5 – 14 | 9.5 | 4 | 38.0 |
| 15 – 24 | 19.5 | 17 | 331.5 |
| 25 – 34 | 29.5 | 19 | 560.5 |
| 35 – 49 | 42.0 | 22 | 924.0 |
| 50 – 64 | 57.0 | 18 | 1026.0 |
| 65 – 79 | 72.0 | 10 | 720.0 |
| कुल | 90 | 3600 |
माध्य \(\bar{x}=\frac{\Sigma f_x}{n}=\frac{3600}{90}\) = 40 इकाई
एक वस्तु की विविध दिन की माँग का माध्य = 40 इकाई है ।