GSEB Solutions Class 11 Statistics Chapter 3 Measures of Central Tendency Ex 3.2

Gujarat Board Statistics Class 11 GSEB Solutions Chapter 3 Measures of Central Tendency Ex 3.2 Textbook Exercise Questions and Answers.

Gujarat Board Textbook Solutions Class 11 Statistics Chapter 3 Measures of Central Tendency Ex 3.2

Question 1.
The mean daily wage paid to 75 skilled workers of a factory was ₹ 280 whereas the mean daily wage paid to 125 unskilled workers was ₹ 150. Find the mean wage of all the workers.
Answer:
Here, n₁ = No. of skilled workers = 75
x̄₁ = Mean of daily wages of skilled workers = ₹ 280
n₂ = No. of unskilled workers =125
x̄₂ = Mean of daily wages of unskilled workers = ₹ 150

Mean of daily wages of workers :
Combined mean x̄_c = \(\frac{n_{1} \bar{x}_{1}+n_{2} \bar{x}_{2}}{n_{1}+n_{2}}\)
Putting n₁ = 75, x̄₁ = 280, n₂ = 125 and x̄₂ = 150 in the formula,
x̄_c = \(\frac{(75 \times 280)+(125 \times 150)}{75+125}\)
∴ x̄_c = \(\frac{21000+18750}{200}\)
∴ x̄_c = \(\frac{39750}{200}\)
∴ x̄_c = ₹ 198.75
Hence, the mean of daily wages of workers = 198.75.

Question 2.
Find the weighted mean of the percentage change in prices from the following data:

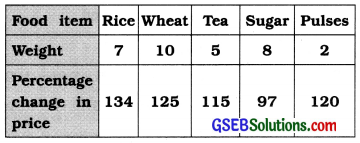
Answer:
Here. weights corresponding to the percentage change in price are given. Therefore, for the calculation of weighted mean the table Isprepared as follows:

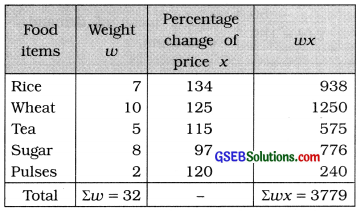
Weighted mean of percentage change of price:
x̄_w = \(\frac{\Sigma w x}{\Sigma w}\)
Putting Σwx = 3779 and Σw = 32 in the formula,
x̄_w = \(\frac{3779}{32}\)
∴ x̄_w = 118.09%
Hence, weighted mean of percentage change in price = 118.09%.

Question 3.
2 officers, 10 clerks and 3 peons contributed for a staff picnic. The contribution collected per person is shown in the following table:

Officer	Clerk	Peon
₹ 1000	₹ 500	₹200

Find the mean contribution per person using weighted mean.
Answer:
For weighted mean, we take the number of staff as weight. calculation is shown in the following table:

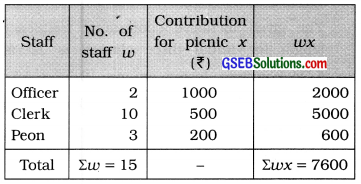
Mean of individual contribution:
x̄_w = \(\frac{\Sigma w x}{\Sigma w}\)
Putting Σwx = 7600 and Σw =15 in the formula,
x̄_w = \(\frac{7600}{15}\)
x̄_w = ₹ 506.67
Hence, mean of individual contribution = ₹ 506.67.

Question 4.
The mean marks of a student in 7 theory papers is 62. What should be the mean marks in 3 practical examinations so that his mean marks for the entire examination is 68?
(The marks of each theory paper and practical examination are the same.)
Answer:
Here, n₁ = No. of theory papers = 7
x̄₁ = Mean of marks of theory papers = 62
n₂ = No. of papers for practical exam = 3
x̄₂ = Mean of marks of practical exam = ?
x̄_c = Mean of marks of theory and practical = 68
Now, x̄_c = \(\frac{n_{1} \bar{x}_{1}+n_{2} \bar{x}_{2}}{n_{1}+n_{2}}\)
Putting x̄_c = 68, n₁ = 7, x̄₁ = 62 and n₂ = 3 in the formula,
68 = \(\frac{(7 \times 62)+\left(3 \times \bar{x}_{2}\right)}{7+3}\)
68 × 10 = 434 + 3x̄₂
3x̄₂ = 680 – 434
3x̄₂ = 246
x̄₂ = \(\frac{246}{3}\)
x̄₂ = 82 marks
Hence, mean of marks of practical exam = 82 marks.