GSEB Solutions Class 11 Statistics Chapter 3 केन्द्रीय स्थिति के माप Ex 3.4

Gujarat Board Statistics Class 11 GSEB Solutions Chapter 3 केन्द्रीय स्थिति के माप Ex 3.4 Textbook Exercise Questions and Answers.

Gujarat Board Textbook Solutions Class 11 Statistics Chapter 3 केन्द्रीय स्थिति के माप Ex 3.4

प्रश्न 1.
किसी एक कक्षा की कसौटी में 15 विद्यार्थियों द्वारा प्राप्त गुण ( नंबर ) की निम्न सूचना पर से सभी चतुर्थक ज्ञात करो ।
8, 6, 7, 0, 2, 4, 6, 5, 5, 4, 7, 9, 3, 6, 7
उत्तर :
सभी चतुर्थक ज्ञात करना है अर्थात् Q₁, Q₂, Q₃ ज्ञात करेंगे । सूचना को चढ़ते क्रम में गठित करने पर
0, 2, 3, 4, 4, 5, 5, 6, 6, 6, 7, 7, 7, 8, 9
Q₁ = \(\frac{n+1}{4}\) वाँ अवलोकन मूल्य
= \(\frac{15+1}{4}=\frac{16}{4}\) = 4 वाँ अवलोकन मूल्य 44
∴ Q₁ = 4 गुण (नंबर)
Q₂ = M = \(\frac{n+1}{2}\) वाँ अवलोकन मूल्य
= \(\frac{15+1}{2}=\frac{16}{2}\) = 8 वाँ अवलोकन मूल्य
∴ Q₂ = 6 गुण (नंबर)
Q₃ = 3 (\(\frac{n+1}{4}\)) वाँ अवलोकन मूल्य
= 3 \(\frac{(15+1)}{4}=\frac{3 \times 16}{4}\)
= 12 वाँ अवलोकन मूल्य
∴ Q₃ = 7 गुण (नंबर)
चतुर्थक Q₁ = 4 गुण (नंबर) Q₂ = 6 गुण (नंबर),
Q₃ = 7 गुण (नंबर) है ।

प्रश्न 2.
एक सेल्समेन अंतिम वर्ष में भिन्न भिन्न दिनों के दौरान की गई सफर (किमी.में ) निम्नानुसार है, उस पर से मध्यका M, Q₃ , D₈ , P₆₂ ज्ञात कीजिए और उसका अर्थघटन कीजिए ।

उत्तर :
संचयी आवृत्तियाँ निम्नलिखित सारणी में प्रदर्शित करेंगे ।

सफर (किमी.)	दिनों की संख्या	संचयी आवृत्ति
0 – 100	05	05
100 – 200	18	23
200 – 300	24	47
300 – 400	07	54
400 – 500	05	59
500 – 600	01	60
कुल	60

⇒ मध्यका (M)
M वर्ग = \(\frac{n}{2}\) वाँ अवलोकन मूल्य
= \(\frac{60}{2}\)
= 30 वाँ अवलोकन का वर्ग संचयी आवृत्ति की सारणी में देखने पर M वर्ग 200 – 300 है ।

अर्थघटन : 50% दिनों के दौरान सफर 229.17 कि.मी. से कम होगी ।
Q₃ = 3 (\(\frac{n}{4}\)) वाँ अवलोकन मूल्य = 3 (\(\frac{60}{4}\))
= 45 वाँ अवलोकन मूल्य संचयी आवृत्ति वितरण में देखने पर Q₃ वर्ग 200 – 300 है ।

अर्थघटन : सबसे कम सफर हुए 75% दिनों में महत्तम अंतर 291.67 कि.मी. होगा ।
D₈ = 8 (\(\frac{n}{10}\)) वाँ अवलोकन मूल्य = 8 (\(\frac{60}{10}\))
= 48 वाँ अवलोकन मूल्य संचयी आवृत्ति की सारणी में देखने पर D₈ वर्ग = 300 – 400

अर्थघटन : सबसे कम सफर हुए 80% दिनों में महत्तम अंतर 314.29 कि.मी. होगा ।
⇒ P₆₂ = 62 (\(\frac{n}{100}\)) वाँ अवलोकन मूल्य
= \(\frac{62 \times 60}{100}\)
= 37.2 वाँ अवलोकन मूल्य संचयी आवृत्ति वितरण में देखने पर P₆₂ वर्ग = 200 – 300 है ।

अर्थघटन : सब से कम सफर हुए 62% दिनों में महत्तम अंतर 259.17 कि.मी. होगा ।

प्रश्न 3.
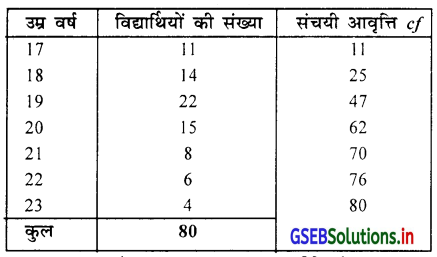
एक कोलेज में से चयन किए 80 विद्यार्थिओं की उम्र निम्न सारणी में प्रस्तुत है।

विद्यार्थियों की उम्र की मध्यका (M) ज्ञात करो ओर उम्र का Q₁, D₄, P₃₂, ज्ञात करो और अर्थघटन करो ।
उत्तर :
आवृत्ति वितरण असतत (खंडित) दिया है । इसलिए निम्न संचयी आवृत्ति प्राप्त करेंगे ।

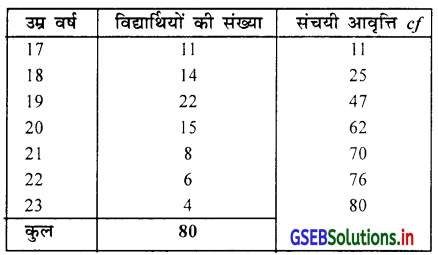
मध्यका M = \(\frac{n+1}{2}\) वाँ अवलोकन मूल्य = \(\frac{80+1}{2}\)
= \(\frac{81}{2}\) = 40.5 वाँ अवलोकन मूल्य cf में देखने पर
∴ M = 19 वर्ष
अर्थघटन : 50% विद्यार्थियों की उम्र 19 वर्ष या उससे कम होगी ।
Q₁ = (\(\frac{n+1}{4}\)) वाँ अवलोकन मूल्य
= \(\frac{80+1}{4}=\frac{81}{4}\) = 20.25 वाँ अवलोकन मूल्य cf की सारणी में देखने पर 18 है
∴ Q₁ = 18 वर्ष
अर्थघटन : 25% विद्यार्थियों की उम्र 18 वर्ष या उससे कम होगी ।
⇒ D₄ = i(\(\frac{n+1}{10}\)) वाँ अवलोकन मूल्य
= 4(\(\frac{80+1}{10}\))
= 4 × 8.1 = 32.4 वाँ अवलोकन मूल्य cf की सारणी में देखने पर 19 है ।
∴ D₄ = 19 वर्ष
अर्थघटन : 40% विद्यार्थियों की उम्र 19 वर्ष या उससे कम होगी ।
⇒ P₃₂ = (\(\frac{n+1}{100}\)) वाँ अवलोकन मूल्य = 32 (\(\frac{80+1}{100}\)) = 32 × 0.81
= 25.92 वाँ अवलोकन मूल्य of की सारणी में देखने पर 18 है ।
∴ P₃₂ = 19 वर्ष
अर्थघटन : 32% विद्यार्थियों की उम्र 19 वर्ष या उससे कम होगी ।

प्रश्न 4.
एक पेढी के कर्मचारियों की निम्न सूचना पर से मध्यका ज्ञात करो । सबसे अधिक वेतन प्राप्त करते 20% कर्मचारियों के वेतन की न्यूनतम सीमा ज्ञात करो ।

उत्तर :
आवृत्ति वितरण ‘से अधिक’ प्रकार का दिया है । इसलिए प्रथम मूल आवृत्ति वितरण ज्ञात करके संचयी आवृत्ति वितरण निम्नानुसार प्राप्त करेंगे।

मध्यका M = \(\frac{n}{2}\) वाँ अवलोकन मूल्य = \(\frac{120}{2}\)
= 60 वाँ अवलोकन मूल्य cf की सारणी में देखने पर M वर्ग = 20 – 25

सबसे अधिक वेतनवाले 20% कर्मचारियों का वेतन की न्यूनतम सीमा ज्ञात करनी है अर्थात् P₈₀ ज्ञात करेंगे ।
P₈₀ = i (\(\frac{n}{100}\)) वाँ अवलोकन मूल्य = \(\frac{80 \times 120}{100}\)
= 96 वाँ अवलोकन मूल्य cf की सारणी में देखने पर P₈₀ वर्ग = 25 – 30

सबसे अधिक वेतनवाले 20% कर्मचारियों का वेतन की न्यूनतम सीमा 21.84 हजार रु. वेतन है ।

प्रश्न 5.
100 विद्यार्थियों के एक समूह में मनोरंजन के पिछे मासिक खर्च का विवरण निम्न सारणी में प्रदर्शित है। उसका माध्यिका (M) ज्ञात करो ।

उत्तर :
मध्यका ज्ञात करने के लिए संचयी आवृत्ति की सारणी बनायेंगे ।

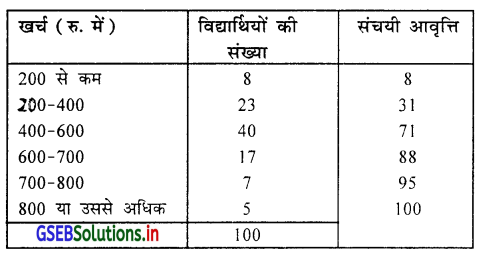
मध्यका (M) = \(n / 2\) वाँ अवलोकन मूल्य
= \(\frac{100}{2}\)
= 50 वाँ अवलोकन मूल्य of में देखने पर M वर्ग = 400 – 600

प्रश्न 6.
निम्न सूचना एक अस्पताल में 30 मरीज के एडमिट के दिनों की पंजीयन है।

एडमिट के दिनों की मध्यका ज्ञात करो । सूचना का प्रथम वर्ग 1-3 हो ऐसा समान वर्गों में सतत आवृत्ति वितरण (अनिवारक)
प्रकार का तैयार करो । आवृत्ति वितरण पर से मध्यका ज्ञात करो और दोनों उत्तर की तुलना करो ।
उत्तर :
अवर्गीकृत सूचना को चढ़ते क्रम में गठित करने पर
1111 2222 3 3333 4444 555 66 77 8 99 1010 15
M = \(\frac{n+1}{2}\) वाँ अवलोकन मूल्य
= \(\frac{30+1}{2}=\frac{31}{2}\)
= 15.5 वाँ अवलोकन मूल्य

= \(\frac{4+4}{2}\) = 8/2
∴ M = 4 दिन
अब 1-3 ऐसे समान वर्ग लंबाईवाला अनिवारक सतत आवृत्ति वितरण प्राप्त करके संचयी आवृत्ति वितरण निम्नानुसार प्राप्त करेंगे ।

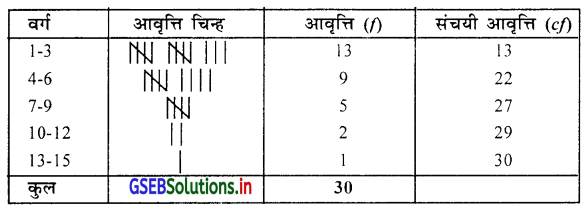
M = n/2 वाँ अवलोकन मूल्य
= \(\frac{30}{2}\) = 15 वाँ अवलोकन मूल्य cf में देखने पर M वर्ग (4 – 6) अनिवारक वर्ग है ।
इसलिए सीमाबिंदु ज्ञात करने पर 4 – 0.5 = 3.5 अधःसीमा बिंदु और 6 + 0.5 = 6.5 उर्ध्वसीमा बिंदु प्राप्त होगा ।
∴ L = 3.5

वर्गीकृत सूचना का मध्यका M = 4.17 दिन, अवर्गीकृत का मध्यका (M) और वर्गीकृत का मध्यका (M) लगभग समान है ।