GSEB Solutions Class 11 Statistics Chapter 4 Measures of Dispersion Ex 4.2

Gujarat Board Statistics Class 11 GSEB Solutions Chapter 4 Measures of Dispersion Ex 4.2 Textbook Exercise Questions and Answers.

Gujarat Board Textbook Solutions Class 11 Statistics Chapter 4 Measures of Dispersion Ex 4.2

Question 1.
A shooter missed his target in the last 10 trials by the following distance (mm) during the practice session:
20, 32, 24, 41, 18, 27, 15, 36, 35, 25
Find the quartile deviation and coefficient of quartile deviation of such distance missed by the shooter.
Answer:
Writing the measures of mistargets in ascending order :
15, 18, 20, 24, 25, 27, 32, 35, 36, 41
Here, n = 10

First Quartile :
Q₁ = Value of \(\left(\frac{n+1}{4}\right)\)th observation
= Value of \(\left(\frac{10+1}{4}\right)\) = 2.75 th observation
= Value of 2nd observation +0.75 (Value of 3rd observation – Value of 2nd observation)
= 18 + 0.75 (20 – 18)
= 18 + 0.75 (2)
= 18 + 1.50 = 19.50 mm

Third Quartile :
Q₃ = Value of 3\([latex]\left(\frac{n+1}{4}\right)\)[/latex] th observation
= Value of 3 (2.75) = 8.25th observation
= Value of 8th observation + 0.25 (Value of 9th observation – Value of 8th observation)
= 35 + 0.25 (36-35)
= 35 + 0.25 = 35.25 mm

Quartile deviation of measures of mistargets :
Q_d = \(\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{2}\)
Putting Q₃ = 35.25; Q1 = 19.50, we get
Q_d = \(\frac{35.25-19.50}{2}=\frac{15.75}{2}\) = 7.875 ≈ 7.88

Coefficient of quartile deviation = \(\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{\mathrm{Q}_{3}+\mathrm{Q}_{1}}\)
= \(\frac{35.25-19.50}{35.25+19.50}\)
= \(\frac{15.75}{54.75}\)
= 0.29

Question 2.
Find the quartile deviation and coefficient of quartile deviation of the marks from the following frequency distribution of marks of 43 students of a school;

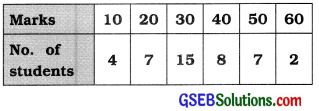
Answer:

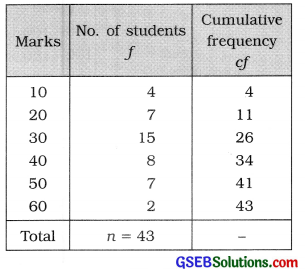
First Quartile :
Q₁ = Value of \(\left(\frac{n+1}{4}\right)\)th observation
= Value of \(\left(\frac{43+1}{4}\right)=\frac{44}{4}\) = 11th observation

Referring to column cf,
Q₁ = 20 marks

Third Quartile :
Q₃ = Value of \(\left(\frac{n+1}{4}\right)\)th observation
= Value of 3(11)
= 33 rd observation Referring to column cf,
Q₃ = 40 marks

Quartile deviation of marks:

Question 3.
The distribution of amount paid by 200 customers coming for snacks at a restaurant on a particular day is given below:

Find the quartile deviation and coefficient of quartile deviation of the amount paid by customers on the day.
Answer:

Amount paid ₹	No. of customers f	Cumulative frequency cf
0-50	25	25
50- 100	40	65
100-150	80	145
150-200	30	175
200 – 250	25	200
Total	n = 200	–

First Quartile:
Q₁ Class = Class that Includes \(\left(\frac{n}{4}\right)\)th observation
= Class that includes \(\left(\frac{200}{4}\right)\) = 50th observation

Referring to column cf
Q₁ class = 50 – 100
Now, Q₁ = L + \(\frac{\left(\frac{n}{4}\right)-c f}{f}\) × c
Putting L = 50: \(\left(\frac{n}{4}\right)\) = 50: cf = 25: f = 40 and c = 50 In the formula,

Third Quartile:
Q₃ Class = Class that Includes 3\(\left(\frac{n}{4}\right)\)th observation
= Class that Includes 3 (50)th = 150th observation
Referring to column cf. Q₃ class = 150 – 200
Now. Q₃ = L + \(\frac{3\left(\frac{n}{4}\right)-c f}{f}\) × c
Putting L = 150: 3\(\left(\frac{n}{4}\right)\) = 150: cf = 145; f = 30 and c = 50 in the formula.