GSEB Solutions Class 11 Statistics Chapter 4 Measures of Dispersion Ex 4.3

Gujarat Board Statistics Class 11 GSEB Solutions Chapter 4 Measures of Dispersion Ex 4.3 Textbook Exercise Questions and Answers.

Gujarat Board Textbook Solutions Class 11 Statistics Chapter 4 Measures of Dispersion Ex 4.3

Question 1.
The measurements of height (in centimeters) of 10 soldiers are given below:

Find the mean deviation of the heights of the soldiers.
Answer:
Here, n = 10

Height (in cm)	| x – x̄ | x̄  = 167.4
160	7.4
175	7.6
158	9.4
165	2.4
170	2.6
166	1.4
173	5.6
176	8.6
163	4.4
168	0.6
Σx = 1674	Σ |x – x̄| = 50.0

Question 2.
The distribution of number of ball bearings used in machines of a factory is given below. Calculate the mean deviation and coefficient of mean deviation of number of ball bearings per machine.

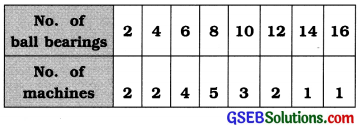
Answer:

Mean:
x̄ = \(\frac{\Sigma f x}{n}=\frac{160}{20}\) = 8 ball bearing

Mean deviation of numbers of ball bearing:
MD = \(\frac{\Sigma f|x-\bar{x}|}{n}\)
= \(\frac{56}{20}\) = 28 ball bearing

Coefficient Mean deviation of ball bearing:
Coefficient of mean deviation = \(\frac{\mathrm{MD}}{\bar{x}}\)
= \(\frac{2.8}{8}\) = 0.35

Question 3.
Find the mean deviation and the coefficient of mean deviation of the distribution of talk time (in minutes) per call.

Answer:


Coefficient of Mean deviation of talk time : Coefficient of Mean deviation = \(\frac{\mathrm{MD}}{\bar{x}}=\frac{3.33}{7.3}\) = 0.46

Question 4.
Find the mean deviation and coefficient of mean deviation of number of TV sets using the following frequency distribution of TV sets sold in last 16 months in a town:

Answer:

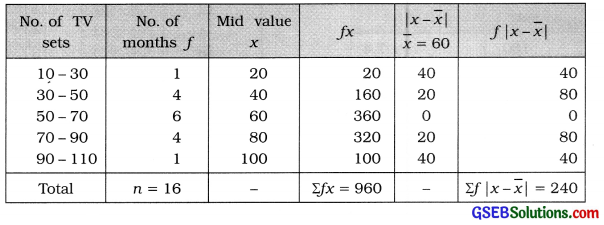
Mean:
x̄ = \(\frac{\Sigma f x}{n}=\frac{960}{16}\) = 60 TV sets

Mean deviation of monthly sales of TV sets:
MD = \(\frac{\Sigma f|x-\bar{x}|}{n}=\frac{240}{16}\) = 15 TV sets

Coefficient of Mean deviation of monthly sales of TV sets:
Coefficient of mean deviation = \(\frac{M D}{\bar{x}}=\frac{15}{60}\) = 0.25

Question 5.
There are 50 boxes containing different number of units of an item in a factory. Find the mean deviation of number of units per box using the following distribution of the units:

Answer:

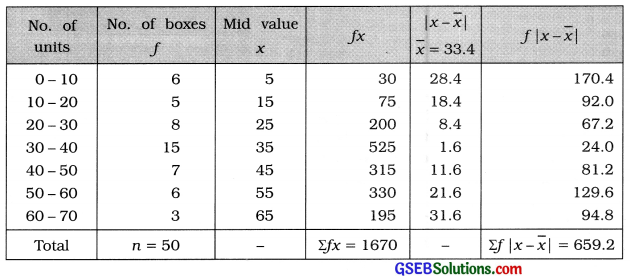
Mean:
x̄ = \(\frac{\Sigma f x}{n}=\frac{1670}{50}\) = 33.4 units

Mean deviation of number of units per box:
MD = \(\frac{\Sigma f|x-\bar{x}|}{n}=\frac{659.2}{50}\) = 13.18 units