GSEB Solutions Class 11 Statistics Chapter 6 क्रमचय, संचय और द्विपद विस्तार Ex 6.2

Gujarat Board Statistics Class 11 GSEB Solutions Chapter 6 क्रमचय, संचय और द्विपद विस्तार Ex 6.2 Textbook Exercise Questions and Answers.

Gujarat Board Textbook Solutions Class 11 Statistics Chapter 6 क्रमचय, संचय और द्विपद विस्तार Ex 6.2

प्रश्न 1.
निम्नलिखित के मूल्य ज्ञात कीजिए :
(1) ¹¹C₄
(2) ⁹C₀
(3) ²⁵C₂₃
(4) ⁸C₈
उत्तर :
(1) ¹¹C₄
ⁿC_r = \(\frac{n !}{r !(n-r) !}\)
¹¹C₄ \(\frac{11 !}{4 !(11-4) !}=\frac{11 \times 10 \times 9 \times 8 \times 7 !}{4 \times 3 \times 2 \times 1 \times 7 !}\) = 330

(2) ⁹C₀
ⁿC₀ = 1 परिणाम के अनुसार
∴ ⁹C₀ = 1
वैकल्पिक रीति ⁿC_r = \(\frac{n !}{r !(n-r) !}=\frac{9 !}{0 !(9-0) !}=\frac{9 !}{1 \times 9 !}\)
∴ = 1

(3) ²⁵C₂₃
ⁿC_r = \(\frac{n !}{r !(n-r) !}\) ²⁵C₂₃ \(\frac{25 !}{23 !(25-23) !}=\frac{25 \times 24 \times 23}{23 ! \times 2 \times 1}\) = 300

(4) ⁸C₈
ⁿC_n = 1
∴ ⁸C₈
वैकल्पिक रीति ⁸C₈ = \(\frac{8 !}{8 !(8-8) !}=\frac{8 !}{8 ! \times 0 !}\) = 1

प्रश्न 2.
अज्ञात संख्या ज्ञात करो ।
(1) ⁿC₂ = 28
(2) ²⁷C_{r + 4} = ²⁷C_{2r – 1}
(3) ⁿC_{n – 2} = 15
(4) 4ⁿC₄ = 7.ⁿC₃
उत्तर :
(1) ⁿC₂ = 28
ⁿC_r = \(\frac{n !}{r !(n-r) !}\)
∴ ⁿC₂ = \(\frac{n !}{2 !(n-2) !}\)
∴ 28 = \(\frac{n(n-1)(n-2) !}{2 \times 1 \times(n-2) !}\)
∴ 56 = n(n – 1)
∴ n(n – 1) = 8 (8 – 1)
∴ n = 8

(2) ²⁷C_{r + 4} = ²⁷C_{2r – 1}
ⁿC_x = ⁿC_y हो तो

विकल्प – 1
x + y = n
r + 4 + 2r – 1 = 27
3r + 3 = 27
∴ 3r = 27 – 3
∴ r = \(\frac{24}{3}\)
∴ r = 8

विकल्प – 2
x = y
r + 4 = 2r – 1
4 + 1 = 2r – r
∴ r = 5

(3) ⁿC_{n – 2} = 15
ⁿC_{n – 2} = ⁿC₂
∴ ⁿC₂ = 15
∴ ⁿC₂ = \(\frac{n !}{2 !(n-2) !}\)
∴ 15 = \(\frac{n(n-1)(n-2) !}{2 \times 1(n-2) !}\)
∴ n(n-1) = 30
∴ 6(6-1) = 30
∴ n = 6

(4) 4.ⁿC₄ = 7.ⁿC₃
\(\frac{4 \times n(n-1)(n-2)(n-3)}{4 \times 3 \times 2 \times 1}\) = \(\frac{7 \times n(n-1)(n-2)}{3 \times 2 \times 1}\)
∴ \(\frac{4 \times(n-3)}{24}=\frac{7}{6}\)
∴ n – 3 = \(\frac{7}{6} \times \frac{24}{4}\)
∴ n – 3 = 7
∴ n = 7 + 3
∴ n = 10

प्रश्न 3.
एक विद्यालय में चपराशी के 2 स्थान के लिए 8 व्यक्ति आवेदन करते है । यह 8 आवेदकों में से 2 चपराशी का चयन कितनी रीति से हो सकता है ?
उत्तर :
8 आवेदकों में से 2 का चयन ⁸C₂ विधि से होगा ।
ⁿC_r = \(\frac{n !}{r !(n-r) !}\)
∴ ⁸C₂ = \(\frac{8 !}{2 !(8-2) !}=\frac{8 !}{2 ! \times 6 !}\) = \(\frac{8 \times 7 \times 6 !}{2 \times 1 \times 6 !}\) = 28

प्रश्न 4.
एक क्रिकेट टुर्नामेन्ट में 5 देश हिस्सा लेते है । यदि प्रथम राउन्ड में प्रत्येक देश को प्रत्येक देश के साथ एक-एक मेच खेलना हो तो कितनी मेच प्रथम राउन्ड में खेली जायेगी ?
उत्तर :
प्रत्येक देश को प्रत्येक देश के साथ खेलना है इसलिए n = 5 अब दो देश खेलते है इसलिए r = 2
कुल प्रकार = ⁵C₂
ⁿC_r = \(\frac{n !}{r !(n-r) !}\)
⁵C₂ = \(\frac{5 !}{2 !(5-2) !}=\frac{5 \times 4 \times 3 !}{2 \times 1 \times 3 !}\) = 10
∴ 10 मेच प्रथम राउन्ड में खेली जायेगी । .
उदा. 1 2 3 4 5 (1 2) (1 3) (1 4) (1 5) (2 3) (2 4) (2 5) (3 4) (35) (4 5) कुल 10 मेच

प्रश्न 5.
एक संदूक में 200 इकाई में से 5% इकाई दोषयुक्त है । यदि संदूक में से 3 इकाई चयन की जाय तो सभी इकाई दोषयुक्त होने के कुल कितने विकल्प हो सकते है ?
उत्तर :
200 इकाई के 5% = 10 दोषयुक्त है । यदि तीन का चयन करना हो तो r = 3, n = 10
सभी दोषयुक्त इकाई ¹⁰C₃ होगा ।
ⁿC_r = \(\frac{n !}{r !(n-r) !}\)
¹⁰C₃ = \(\frac{10 !}{3 !(10-3) !}=\frac{10 \times 9 \times 8 \times 7 !}{3 \times 2 \times 1 \times 7 !}\)
= 120 विकल्प

प्रश्न 6.
एक बैंक में नौकरी करते 14 क्लार्क और 6 चपराशी में से 3 क्लार्क और 1 चपराशी का चयन कितनी तरह से हो
सकता है ?
उत्तर :
14 क्लार्क में से 3 क्लार्क ¹⁴C₃ और 6 चपराशी में से 1 चपराशी का चयन ⁶C₁ रीति से होगा ।
∴ चुनाव के कुल प्रकार = ¹⁴C₃ × ⁶C₁
= \(\frac{14 !}{3 !(14-3) !} \times \frac{6 !}{1 !(6-1) !}\)
= \(\frac{14 \times 13 \times 12 \times 11 !}{3 \times 2 \times 1 \times 11 !}\) × \(\frac{6 \times 5 \times 4 \times 3 \times 2 \times 1}{1 \times 5 \times 4 \times 3 \times 2 \times 1}\)
= 346 × 6 = 2184

प्रश्न 7.
एक टोकरी में 3 सफेद और 5 गुलाबी फूल है । उसमें से
(1) एक ही रंग के तीन फूल कितनी रीति से चयन कर सकते है ?
(2) भिन्न-भिन्न रंग के दो फूल कितनी रीति से चयन कर सकते है ?
उत्तर :
(1) एक ही रंग के तीन फूल अर्थात् तीनों सफेद अथवा तीनों गुलाबी फूल होंगे ।
∴ एक ही रंग के फूल हो ³C₃ + ⁵C₃
ⁿC_r = \(\frac{n !}{r !(n-r) !}\) = \(\frac{3 !}{3 !(3-3) !}+\frac{5 !}{3 !(5-3) !}\)
= \(\frac{3 !}{3 ! \times 1}+\frac{5 \times 4 \times 3 !}{3 ! \times 2 \times 1}\) = 1 + 10 = 11

(2) भिन्न-भिन्न रंग के दो फूल हो अर्थात् एक सफेद और एक गुलाबी हो :
∴ भिन्न-भिन्न रंग के फूल = ³C₁ + ⁵C₁ = 3 × 5 = 15

प्रश्न 8.
52 पत्तों की तास की गड़ी में से दो पत्ते यादृच्छिक रूप से लिए जाते है ।
(1) दोनों पत्ते पान के कितनी रीति से चयन कर सकते है ?
(2) एक पत्ता बादशाह का और एक पत्ता बेगम का कितनी रीति से चयन कर सकते है ?
उत्तर :
(1) पान के 13 पत्ते होते है उसमें से दोनों पान के ¹³C₂ रीति से चयन होगा ।
∴ दोनों पत्ते पान के हो = ¹³C₂
ⁿC_r = \(\frac{n !}{r !(n-r) !}\)
¹³C₂ = \(\frac{13 !}{2 !(13-2) !}=\frac{13 \times 12 \times 11 !}{2 \times 1 \times 11 !}\) = 78

(2) एक बादशाह का और एक बेगम का हो उसका चयन ⁴C₁ और ⁴C₁ होगा ।
∴ एक बादशाह का और एक बेगम का हो ⁴C₁ × ⁴C₁
∴ 4 × 4 = 16

प्रश्न 9.
एक बैंक के 9 कर्मी में 6 क्लार्क, 2 चपराशी और 1 मेनेजर है । उसमें से 4 सदस्यों की समिति की रचना करनी है ।
(1) यदि मेनेजर को समिति में रखना ही हो तो समिति कितने प्रकार से निर्मित की जा सकेगी ?
(2) यदि समिति में दो चपराशी को न रखना हो और मेनेजर का चयन करना ही हों तो समिति कितने प्रकार से निर्मित की जा सकेगी ?
उत्तर :
(1) यदि मेनेजर को समिति में रखना हो तो 4 सदस्यों की समिति ¹C₁ × ⁸C₃ रीति से हो सकेगी।
∴ 1 × \(\frac{8 \times 7 \times 6}{3 \times 2 \times 1}\) = 1 × 56 = 56

(2) यदि चपराशी को न रखना हो और मेनेजर को समिति में रखना हो तो चयन ¹C₁ × ⁶C₃
∴ 1 × \(\frac{6 \times 5 \times 4}{3 \times 2 \times 1}\) = 1 × 20 = 20

प्रश्न 10.
एक ओफिस में कार्यरत 8 कर्मीयों में 3 स्त्रियों और शेष पुरुष है । प्रशिक्षण हेतु 3 सदस्यों की समिति की रचना करनी है, जिस में कम से कम एक व्यक्ति पुरुष का कितने प्रकार से चयन की जा सकती है ?
उत्तर :
कम से कम एक व्यक्ति पुरुष हो उसके विकल्प निम्नलिखित है ।
(1) एक पुरुष और 2 स्त्री
अथवा
(2) दो पुरुष और 1 स्त्री
अथवा
(3) तीन पुरुष 0 स्त्री
चुनाव के कुल प्रकार = ⁵C₁ × ³C₂ + ⁵C₂ × ³C₁ + ⁵C₃ × ³C₀
= 5 × \(\frac{3 \times 2}{2 \times 1}\) + \(\frac{5 \times 4}{2 \times 1}\) × 3 + \(\frac{5 \times 4 \times 3}{3 \times 2 \times 1}\) × 1 = 5 × 3 + 10 × 3 + 10 × 1
= 15 + 30 ++10 = 55

प्रश्न 11.
एक व्यक्ति को 6 मित्र है। इसमें से कम से कम एक मित्र को आमंत्रण कितने प्रकार से दे सकेगा ?
उत्तर :
आमंत्रण के निम्न प्रकार बनेगे ।
कम से कम एक मित्र को आमंत्रण देना है ।
एक मित्र को अथवा दो मित्र को अथवा 3 मित्र को अथवा 4 मित्र को अथवा 5 मित्र को अथवा 6 मित्र को आमंत्रण दे सकता है। आमंत्रण के कुल प्रकार = ⁶C₁ + ⁶C₂ + ⁶C₃ + ⁶C₄ + ⁶C₅ + ⁶C₆
= 6 + \(\frac{6 \times 5}{2 \times 1}\) + \(\frac{6 \times 5 \times 4}{3 \times 2 \times 1}\) + \(\frac{6 \times 5}{2 \times 1}\) + 6 + 1
= 6 + 15 + 20 + 15 + 6 + 1 = 63
∴ कम से कम एक मित्र के आमंत्रण 63 प्रकार से दे सकता है ।

प्रश्न 12.
8 भिन्न-भिन्न पुस्तक में से 5 पुस्तक का चयन कितनी रीति से हो सकेगा की जिसमें
(1) कोई एक निश्चित पुस्तक हमेशा चुनी जाय ।
(2) कोई एक निश्चित पुस्तक का चुनाव न हो ।
उत्तर :
(1) कोई एक निश्चित पुस्तक का चुनाव हमेशां हो उसके
कुल प्रकार = ¹C₁ × ⁷C₄
= 1 × \(\frac{7 \times 6 \times 5 \times 4}{4 \times 3 \times 2 \times 1}\) = 1 × 35 = 35

(2) किसी एक पुस्तक का चुनाव न हो उसके
कुल प्रकार = ¹C₀ × ⁷C₅
= 1 × \(\frac{7 \times 6 \times 5 !}{5 !(7-5) !}\) = 1 × \(\frac{7 \times 6 \times 5 !}{5 ! \times 2 \times 1}\) = 1 × 21 = 21

प्रश्न 13.
कक्षा 12 की सामान्य प्रवाह की बोर्ड की परीक्षा में कोई विद्यार्थी कुल 7 विषयों की परीक्षा देना है । परीक्षा में उत्तीर्ण होने के लिए सभी विषयों में उत्तीर्ण होना अनिवार्य है । प्रत्येक विषय में उत्तीर्ण होने के लिए कम से कम निश्चित नंबर प्राप्त करना हो, तो परीक्षा में उपस्थित विद्यार्थी कितनी रीति से अनुत्तीर्ण होगा ?
उत्तर :
अनुत्तीर्ण के लिए निम्न विकल्प होंगे ।
एक विषय में अनुत्तीर्ण अथवा 2 विषय में अनुत्तीर्ण, अथवा 3 विषय में अनुत्तीर्ण अथवा 4 विषय में अनुत्तीर्ण, अथवा 5 विषय में अनुत्तीर्ण, अथवा 6 विषय में अनुत्तीर्ण अथवा 7 विषय में अनुत्तीर्ण
कुल प्रकार = ⁷C₁ + ⁷C₂ + ⁷C₃ + ⁷C₄ + ⁷C₅ + ⁷C₆ + ⁷C₇
= 7 + \(\frac{7 \times 6}{2 \times 1}\) + \(\frac{7 \times 6 \times 5}{3 \times 2 \times 1}\) + \(\frac{7 \times 6 \times 5}{3 \times 2 \times 1}+\frac{7 \times 6}{2 \times 1}\) + 7 + 1
= 7 + 21 + 35 + 35 + 21 + 7 + 1 = 127

प्रश्न 14.
एक होटेल का मालिक शहर में उपलब्ध 8 भिन्न-भिन्न समाचारपत्रों और 5 भिन्न-भिन्न सामायिक में से 3 समाचारपत्रों और 2 सामायिकों हररोज मँगवाना चाहता है। चयन कितनी रीति से कर सकते है ? यदि निश्चित समाचारपत्र का चयन हमेशा करना हो और यदि किसी निश्चित सामायिक का चयन न करना हो तो ऐसा चयन कितने प्रकार से कर सकते है ?
उत्तर :
8 भिन्न-भिन्न समाचारपत्रों में से 3 समाचारपत्रों का चयन ⁸C₃ और 5 भिन्न-भिन्न सामायिकों में से 2 का चयन ⁵C₃ रीति से होगा ।
कुल प्रकार = ⁸C₃ + ⁵C₃ = \(\frac{8 !}{3 !(8-3) !} \times \frac{5 !}{3 !(5-3) !}\)
= \(\frac{8 \times 7 \times 6 \times 5 !}{3 \times 2 \times 1 \times 5 !}\) = \(\frac{5 \times 4 \times 3 !}{3 ! \times 2 \times 1}\) = 56 × 10 = 560

⇒ यदि निश्चित समाचारपत्र का चयन करना हो तो और निश्चित सामायिक का चयन न करना हो तो चयन ¹C₁ × ⁴C₂ और सामायिक का चयन न करना हो तो ⁴C₂ रीति से चयन होगा ।
∴ कुल प्रकार = ¹C₁ × ⁷C₂ × ⁴C₂
= 1 × \(\frac{7 \times 6}{2 \times 1} \times \frac{4 \times 3}{2 \times 1}\) = 1 × 21 × 6 = 126

प्रश्न 15.
ⁿP₂ + ⁿC₂ = 84 हो, तो n का मूल्य ज्ञात करो । उत्तर :
ⁿP₂ + ⁿC₂ = 84
\(\frac{n !}{(n-r) !}\) + \(\frac{n !}{r !(n-r) !}\) = 84
∴ \(\frac{n(n-1)(n-2) !}{(n-2) !}\) + \(\frac{\mathrm{n}(\mathrm{n}-1)(\mathrm{n}-2) !}{2 !(\mathrm{n}-2) !}\) = 84
∴ n (n – 1) + \(\frac{\mathrm{n}(\mathrm{n}-1)}{2}\) = 84 (L.C.M. लेने पर)
∴ 2(n) (n – 1) + (n) (n – 1) = 84 × 2
∴ 2 (n² – n) + (n² – n) = 168
∴ 2n² – 2n + n² – n = 168
∴ 3n2 – 3n = 168
∴ 3n (n – 1) = 168
∴ n(n – 1) = \(\)
∴ n(n – 1)=56
∴ 8(8 – 1)=56
8 × 7 = 56
∴ n = 8

प्रश्न 16.
यदि ⁿP_r ÷ ⁿC_r = 24 हो, तो r का मूल्य ज्ञात करो ।
उत्तर :
ⁿP_r + \(\frac{n !}{(n-r) !}\) और ⁿC_r = \(\frac{n !}{r !(n-r) !}\)
अब \(\frac{n !}{(n-r) !}\) ÷ \(\frac{n !}{r !(n-r) !}\) = 24
∴ \(\frac{n !}{(n-r) !}\) × \(\frac{r !(n-r) !}{n !}\) = 24
r! = 24
∴ r! = 4 × 3 × 2 × 1
∴ r! = 4!
r = 4

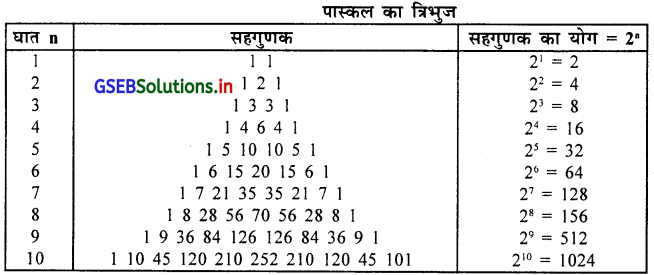
⇒ द्विपद विस्तार : यदि पदावलि में दो पद हो और दोनों के बीच धन या ऋण चिन्ह हो ऐसी पदावलि को द्विपद पदावलि कहते है । उस प्रकार की द्विपद पदावलि को कितने ही धनपूर्णांक घात देकर उनका विस्तार किया जा सकता है । विस्तार करने की पद्धति को द्विपद विस्तार कहा जाता है ।
द्विपद विस्तरण के सहगुणक को त्रिभुज स्वरूप में निम्न प्रदर्शित कर सकते है ।